向量投影的拓展学习
●任旭英 (杭州第九中学 浙江杭州 310020)
向量投影的拓展学习
●任旭英 (杭州第九中学 浙江杭州 310020)
平面向量在高考中的考查从粗浅转向深入,向量投影的考查成为一个热点.如:

A.∠ABC=90° B∠BAC=90°
C.AB=AC D.AC=BC
(2013年浙江省数学高考理科试题第7题)
首先回顾向量投影的概念和它的几何性质:若θ是a与b的夹角,则|b|cosθ叫做向量b在a方向的投影.当b⊥a时,向量b在a方向的投影为0.当b与a不垂直时,向量b在a方向的投影就是有向线段(如图1和图2),图1中的有向线段是正的,而图 2 中的有向线段是负的.

图1

图2
对于非零向量 a=(x1,y1)与 b=(x2,y2),利用 a·b=|a|·|b|cosθ和 a·b=x1x2+y1y2,向量b在a方向的投影可用下面的2个公式计算:

下面举例说明:
1 利用向量投影求三角形的高

利用投影来计算高线长,比通过列方程求垂足坐标的方法,步骤少,计算量少,可提高计算的准确率,同时使学生更进一步理解向量运算.
2 利用向量投影推导点到线的距离公式
例3已知直线l的方程为Ax+By+C=0,点Q(x0,y0),求点Q到直线l的距离.

利用投影公式计算距离,比教科书中构造直角三角形利用勾股定理计算距离思路更清晰,计算量更少,可把繁琐的计算推理转化成巧妙的构思计算,从而感受到数学的简洁美.

图3

图4
3 利用向量投影推导三角形面积公式

注以AB与AC为邻边构成的平行四边形的面积为|x1y2-x2y1|.
如果用余弦定理和正弦定理来计算三角形的面积,估计很少有学生能给出答案.答案的简洁和对称,会给学生震撼和成就感.
4 利用向量投影解决解析几何大题
例5已知曲线C是到点和到直线距离相等的点的轨迹.l是过点Q(-1,0)的直线,M是C上(不在l上)的动点,A,B在l上,MA⊥l,MB⊥x轴(如图5).
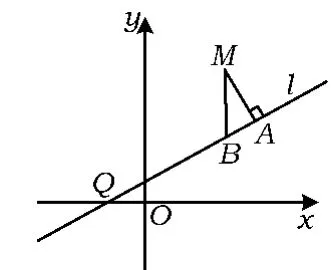
图5
(1)求曲线C的方程;
(2008年浙江省数学高考理科试题第20题)

3(x1+x2)(x1-x2)-4(y1+y2)(y1-y2)=0.因为直线AB不过原点,所以x1+x2≠0.当直线AB与x轴垂直时,直线AB的方程为x=0,与不过原点的条件不符,故x1-x2≠0,于是

上述2个题目在高考中,因其烦琐的运算,考生的得分很低.但利用向量的方法解决问题时,学生解题的正确率与速度都大大地提高了.
向量投影的学习,有助于学生更好地用代数方法处理几何问题,也能从中感受到数学的魅力.本文从向量投影的角度来解决问题,使学生能初步感受向量投影在求距离或求面积时的通用性和优势.

