一道高中数学联赛试题的探究与发现

●吴建山 (龙海市第二中学 福建龙海 363110)

一道高中数学联赛试题的探究与发现

●吴建山 (龙海市第二中学 福建龙海 363110)

题目给定椭圆C：⊙O：x2+y2=b2，自椭圆上异于其顶点的任意一点P作⊙O的2条切线，切点分别为M，N，若直线MN在x轴、y轴上的截距分别为m，n，证明

(2010年全国高中数学联赛江西省预赛试题)

1 探索

试卷提供的解法较为繁琐，且技巧性较高.其实，运用“设而不求”的数学思想，容易得到本题的如下简洁证法.

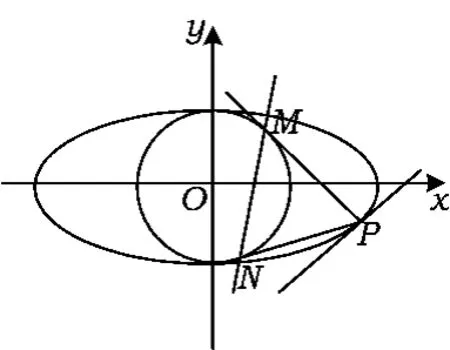
图1

证明如图1，设 P(x0，y0)，M(x1，y1)，N(x2，y2)，则2条切线PM，PN的方程分别为

x1x+y1y=b2，x2x+y2y=b2.由点P在2条切线上，知

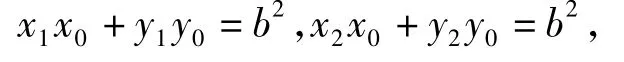
因此直线MN的方程为

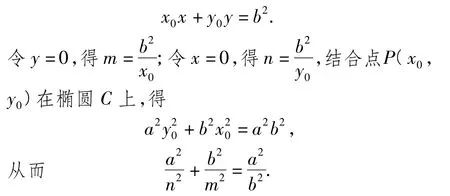
2 发现

若对图形作探究，不难发现，随着点P的运动，椭圆在点P处的切线与切点弦都作相应变化，它们的斜率之间是否存在某种内在联系呢?由以上的证明可知，切点弦MN的斜率为而椭圆在点P处的切线方程为

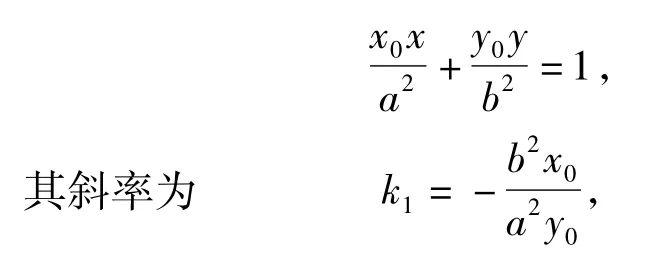
3 拓展

将上述结论拓广至椭圆与双曲线，以及圆与双曲线，可得如下有趣性质.

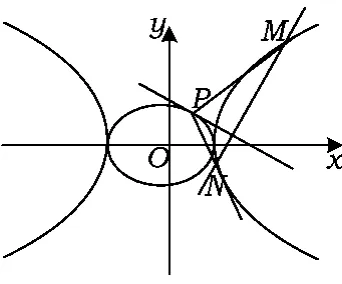
图2

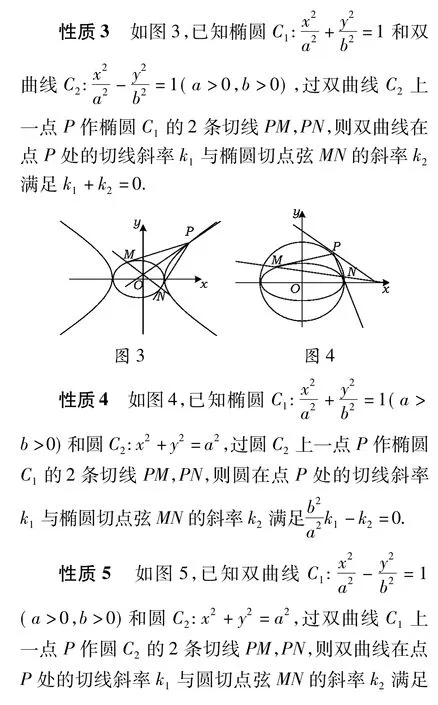
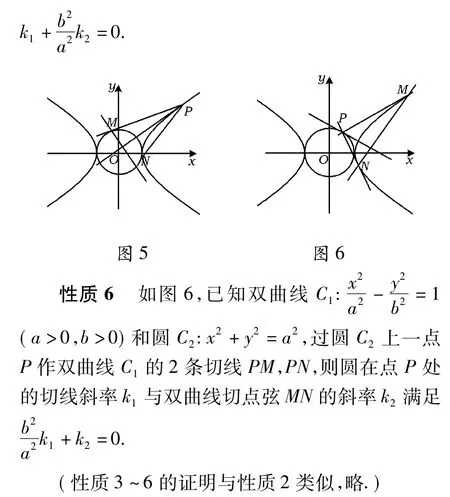
［1］林新建.“情侣圆锥曲线”的有趣性质及其拓广［J］.数学通报，2010(7)：58-60.

［2］玉云化.共焦点的圆锥曲线的切线性质［J］.数学通讯，2009(3)：27-28.