抓“题根” 重变式 以不变应万变——高三二轮复习的点滴思考

●耿道永 (苏州市工业园区第二高级中学 江苏苏州 215121)

抓“题根” 重变式 以不变应万变
——高三二轮复习的点滴思考

●耿道永 (苏州市工业园区第二高级中学 江苏苏州 215121)

以“全面掌握基础知识、准确理解基本概念、深刻领悟基本思想、熟练运用基本方法”为主旨的的一轮复习已经结束，高三数学进入了二轮复习阶段.二轮复习是由“量的积累”到“质的飞跃”即“由厚到薄”的过程，是形成知识网络化、条理化以及全面提升能力的关键时期，素有“二轮看水平”之说.因此如何恰当选题、设计题目，如何提炼、总结解题方法是二轮复习的关键.

木有本，水有源，题有根.我们若能将浩瀚的题目分门别类，找出同一类试题的题祖，探索其常用解法，则能达到举一反三、跳出题海的目的.所谓“题根”，可以是课本上的例题、习题，考卷上的考题，也可以是自己编辑的题目.这个题目首先要基础，80%以上的学生能解决;其次这个题型是高考的热点，由它可以生长成很多优秀的试题;最后这道题的解法要有普遍的适用性，能解决一类的题目.二轮复习中利用题根教学有以下3个作用：

1 体现差异教学理念，满足不同学生的需要

差异教学是指在班集体教学中，立足学生的个性差异，满足不同学生的学习需要，促进每个学生最大限度发展的教学.差异教学尊重学生之间的差异，本着公平和和谐发展的原则，力争让每个学生都学有所获，都能获得更大发展.题根教学起点低，思维开阔，并且不断向纵深发展，可以实现差异教学的目的.

题根1若正数 a，b满足 ab=a+b，求 a+b的最小值.

分析本题是一道很经典的题目，大多数学生都能做出来，主要有以下几种方法：

思路1题设中既有a+b，也有ab，而结果只含有a+b.利用基本不等式把ab放缩成和的形式，从而达到化异为同的目的.

思路2对于多元问题，一种通法就是消元转化，一般转化为函数来处理.

思路3题设2边同时除以ab，可得1，利用“1”的代换求解.

思路4一般求和的最小值，可以联想设法拼凑积为定值.由

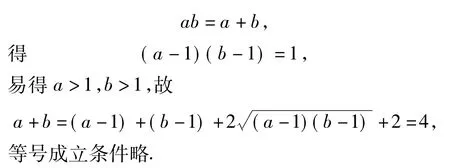
思路5题设中既有a+b，也有ab，联想韦达定理，构造方程求解.

精心预设多种方法，为学生的思维差异、认知差异作好铺垫.针对每个学生的想法，教师都要善于挖掘其合理成分，最大限度地发挥其主观能动性.当然，作为教师，必须指出思路1和思路2是适用性比较强的方法，也就是所谓的通法.

本题若是到此结束，虽然能提炼出思想方法，满足了不同思维方式学生的需要，但是作为题根的功能还没有提炼出来.思维能力强、基础好的学生收获不大，还未能最大限度地满足不同层次学生的需要，为此作如下3个层次的变式：

改编层次1改变系数

这种改编最容易，上面提到的5种方法基本都能用.

变式 1.1若正数 x，y满足 x+3y=5xy，则3x+4y的最小值是 ( )

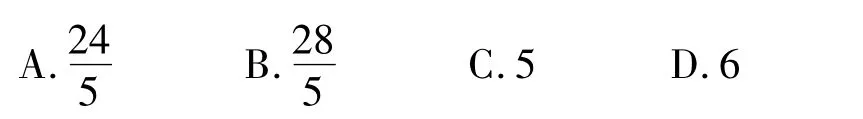
(2012年浙江省数学高考文科试题)

变式1.2已知 a ＞0，b＞0，a+b=2，则 y=的最小值是 ( )

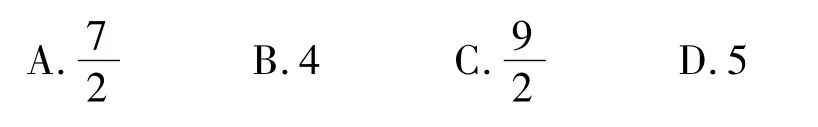
(2011年重庆市数学高考理科试题)

变式1.3若正实数x，y满足2x+y+6=xy，则xy 的最小值是 .

(2010年浙江省数学高考文科试题)

改编层次2披上“神秘的面纱”

题根不刻意对学科内容在形式上的覆盖，但着重考虑题根与题根之间自然的、深刻的、纵横的渗透.因为覆盖的只是一个“平面”，而渗透将得到一个“三维立体”.该题根可以披上“圆锥曲线、指对数函数、数列、立体几何”等神秘的面纱，有待我们发现其“庐山真面目”.

变式1.4已知f(x)=log2(x－2)，若实数m，n满足 f(m)+f(2n)=3，则 m+n 的最小值是＿＿.

(江苏省南京市2011届高三第一次模拟考试题)

变式1.5已知各项为正数的等比数列{an}满足 a7=a6+2a5，若 存 在 项 am，an，使 得

(2012年上海市徐汇区高三第一次模拟考试题)

变式1.5在三棱锥P-ABC中，PA，PB，PC两两垂直，且 PA=3，PB=2，PC=1.设 M 是底面△ABC 内一点，定义 f(M)=(m，n，p)，其中 m，n，p分别是三棱锥M-PAB，M-PCB，M-PAC的体积.若

改编层次3“元数”升级或者“次数”升级

题根具有生长性，通过增加变元或者升级“次数”，可以使简单题目升级为中档题，中档题升级为难题.这些题目貌似新颖，解决的方法只要类比题根的解法即可.

变式1.6设x，y为实数，若4x2+y2+xy=1，则2x+y 的最大值是 .

(2011年浙江省数学高考理科试题)

变式1.7设 x，y是正实数，且 x+y=1，则

(2012～2013学年江苏省扬州市高三数学期末试题)

变式1.8已知实数 a，b，c满足 a+b+c=9，ac+bc+ca=24，则 b 的取值范围是 .

(江苏省徐州市2011届高三第一次调研试题)

2 构建整体知识网络，提炼通用思想方法

二轮复习时间短，很难做到面面俱到，应抓住核心热点问题重点复习，设法形成知识体系，注重知识的不断深化，关注不同章节知识之间的内在联系，让看似杂乱的知识联系起来，构建知识网络，完善认知结构.数学知识网络应当是立体的、交叉的，单一的线状连接难以适应变化;数学知识网络应当是可延伸的，应随时接纳新的信息，不断丰富、不断完善.将这些知识有机联系在一起的往往是思想方法，思想方法是一条暗线，需要师生共同提炼.题根1基本做到了强化热点基础知识，沟通不同知识联系的目的，提炼思想方法(消元转化、换元转化、函数方程、常数代换)的目的.

题根2已知圆C：(x－a)2+(y－b)2=r2和直线l：Ax+By+C=0相离，d为圆心C到直线l的距离，则圆上的点到直线l的最大距离为r+d，最小距离为r－d.

纵横联系1改变设问方式，建立直线与圆、数与形之间的知识体系

变式2.1已知点 P(x，y)是圆 C：x2+y2－4x－4y－10=0上一点，求|x+y－12|的最大值.

变式2.2已知圆 C：x2+y2－4x－4y－10=0和直线l：x+y－12=0，点P是直线l上一点，过点P作圆的切线PA(A为切点)，则PA 的最小值为.

变式2.3已知圆 C：x2+y2－4x－4y－10=0和直线l：x+y－12=0，点P是直线l上一点，过点P作圆的切线 PA，PB(A，B为切点)，求四边形PACB面积的最小值.

变式2.4已知圆 C：x2+y2－4x－4y－10=0和直线l：x+y－12=0，点P是直线l上一点，过点P作圆的切线 PA，PB(A，B为切点).当∠APB最大时，点P 的坐标为 .

反思本题还可以加上一件华丽的外衣：条件不变的情况下求的最小值.注意到因此转化为求cos∠ACB的最小值，也就相当于求∠APB的最大值.

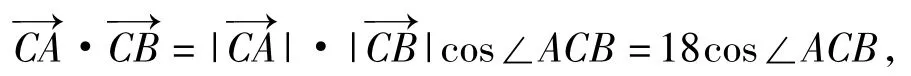
变式2.5在平面直角坐标系xOy中，圆C的方程为 x2+y2－8x+15=0，若直线 l：y=kx－2 上至少存在一点，使得以该点为圆心、1为半径的圆与圆C有公共点，则k 的最大值是 .

(2012年江苏省数学高考试题)

纵横联系2将直线换成点、圆，构建点与圆、圆与圆的知识体系

变式2.6圆 C：x2+y2－4x－4y－10=0上的点P到定点D(－2，－1)的最大距离与最小距离的差是 .

变式 2.7若实数 a，b，c成等差数列，点P(－1，0)在动直线ax+by+c=0上的射影为M，点N(3，3)，则线段 MN 长度的最大值是 .

(2012年苏州大学高考预测卷试题)

分析由题可知2b=a+c，故动直线ax+by+c=0 过定点 A(1，－2).设点M(x，y)，由MP⊥MA可求得点M的轨迹方程为圆.因此问题转化为圆上的点M和定点N距离的最大值问题.

变式2.8已知圆 C：x2+y2－4x－4y－10=0上一点(x，y)，求x2+y2的最大值和最小值.

纵横联系3将圆换成抛物线、椭圆或者一些函数的图像，沟通解析几何、函数等知识之间的联系

变式2.9定义：曲线C上的点到直线l的距离的最小值称为曲线C到直线l的距离.已知曲线C1：y=x2+a到直线 l：y=x的距离等于曲线 C2：x2+(y+4)2=2到直线l：y=x的距离，则实数a=.

(2012年浙江省数学高考文科试题)

变式2.10分别在曲线y=ex和直线y=ex－1上各取一点M和N，则MN 的最小值为 .

(2013年江苏省苏州市二模试题)

以上各题在构建整体知识网络的同时，还可以提炼数形结合、化归转化、联想构造等通性通法，达到了整合热点知识、提高学生解题能力的目的.

3 透析高考命题视角，知己知彼有的放矢

高考试题以改编为主，改编的原型多出于一些经典的问题.了解一些命题视角，对于教师用活一些经典的题目、提高课堂教学的针对性大有裨益.

题根3(阿波罗尼斯圆) 在平面上给定2个点A，B，设点P在同一平面上且满足当λ＞0且λ≠1时，点P的轨迹是圆，这个圆我们称之为“阿波罗尼斯圆”，这个结论称作“阿波罗尼斯轨迹”.

阿波罗尼斯圆的性质在线段AB关于定比λ(λ≠1)的阿波罗尼斯圆上任意一点C，到点A，B距离的比都等于定比λ，即.若此圆与线段AB以及它的延长线交于点M，N，则CM，CN分别是∠ACB的内角平分线和外角平分线.

也就是说，阿波罗尼斯圆的性质和阿波罗尼斯轨迹定理是一组互逆命题，这是一些试题命制的依据.

命题视角1演绎法

这是一种从一般真命题或一组条件出发，通过逻辑推理编制数学习题的方法.

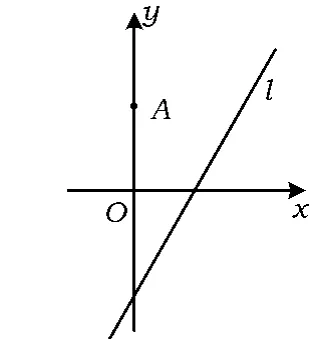
图1

变式3.1如图1，在平面直角坐标系 xOy中，点 A(0，3)，直线 l：y=2x－4.设圆 C 的半径为1，圆心在l上.

(1)若圆心C也在直线y=

x－1上，过点A作圆C的切线，求切线的方程;

(2)若圆C上存在点M，使MA=2MO，求圆心C的横坐标a的取值范围.

(2013年江苏省数学高考试题)

分析本题解决的难点在于探求动点M的轨迹方程，而点M的轨迹就是著名的阿波罗尼斯圆.

变式3.2已知定点 A( －2，0)，B(1，0)，如果动点P满足|PA|=2|PB|，则点P的轨迹包围的图形面积等于 ( )

A.π B.4π C.8π D.9π

(2006年四川省数学高考试题)

变式3.3设 A( － c，0)，B(c，0)(c＞0)为 2个定点，动点P到点A的距离与到点B距离的比为定值a，求点P的轨迹方程及图形.

(2003年北京市春季数学高考试题)

命题视角2改编法

就是直接将概念、定理、成题改编为题目，常用的方法有：仿造、推演、转化、改变信息形态、改编条件和结论等.

(2008年江苏省数学高考试题)

分析本题解法较多，比较简单的解法是发现点A的轨迹是阿波罗尼斯圆，从而以AB所在直线为x轴、AB的中垂线为y轴建立直角坐标系，求出点C的轨迹方程，从而求得△ABC面积的最大值为

反思本题不是直接考查阿波罗尼斯圆，而是把它作为解决问题的一种手段，体现命题者思维的开阔性、创造性.

变式3.5如图2，圆O1与圆O2的半径都是1，O1O2=4，过动点 P分别作圆 O1，圆 O2的切线PM，PN(M，N分别为切点)，使得，试建立适当的坐标系，并求动点P的轨迹方程.

(2005年江苏省数学高考试题)

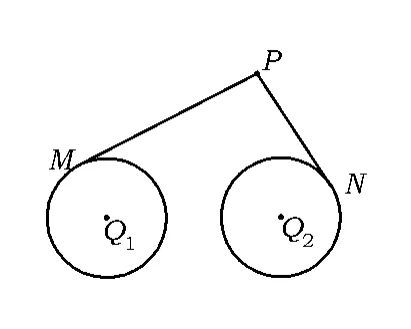
图2

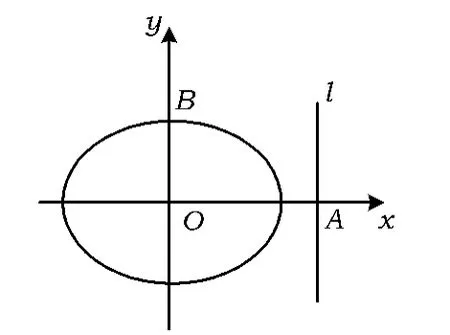
图3

命题视角3倒推法

这是一种利用命题可逆性的命题方法，即知道命题的结论，探索命题的题设.如在已知圆的前提下，探求定点和比值可以命制更为复杂的试题.

变式3.6如图3，已知椭圆 E：(a＞b＞0)的离心率为，且过点，设椭圆的右准线l与x轴的交点为A，椭圆的上顶点为B，直线AB被以原点为圆心的圆O所截得的弦长

(1)求椭圆E的方程及圆O的方程.

(2)若M是准线l上纵坐标为t的点，求证：存在一个异于M的点Q，对于圆O上任意一点N，有为定值;且当M在直线l上运动时，点Q在一个定圆上.

(2011年3月苏、锡、常、镇四市高三数学教学情况调查题)

分析对于第(2)小题，容易联想到阿波罗尼斯圆的性质，解决这类题一般的方法是：设出点和定比，利用多项式恒等探求出点的坐标和定比的值.阿波罗尼斯圆涉及：1个圆、2个定点、1个定比，考题常常围绕这5个量做文章.

命题视角4模型法

以阿波罗尼斯圆为模型，创设一个实际应用背景，或者从实际问题中抽象出阿波罗尼斯圆模型，考查学生分析、综合、概括、抽象的能力.

变式 3.7如图 4，铁路线上线段 AB=100 km，工厂C到铁路的距离CA=20 km.现要在A，B之间某一点D处，向C修一条公路.已知每吨货物运输1 km的铁路费用与公路费用之比为3∶5，为了使原料从供应站B运到工厂C的费用最少，点D应选在何处?

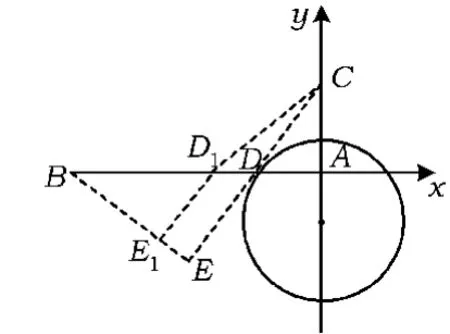
图4

分析先求到定点A，C的距离之比为的动点P(x，y)的轨迹方程(阿波罗尼斯圆)，所求圆的方程和线段AB的交点D即为所求，可以用平面几何知识证明，这里从略.

以上考题提醒一线的教师和学生，要理解一些重要定理与结论产生的背景、发现过程以及蕴含的思想方法.体验貌似不同的考题内在的联系，感悟数学的美，发掘考题的根，这样才能在高考中以不变应万变，取得理想成绩，也会使部分师生真正喜欢上数学，投入到数学研究中去.

二轮复习不是简单地做一些综合题，题成山，题成海，茫茫题海，寻“根“是岸.精选题根，合理变式，才能从茫茫题海中走出来，才能提高二轮复习的有效性，才能全面提高学生分析问题、解决问题的能力.

［1］华国栋.差异教学策略［M］.北京：北京师范大学出版社，2010.

［2］耿道永.一类不等式的题根［J］.中小学数学：高中版，2013(3)：46-48.

［3］耿道永.茫茫题海 寻“根”是岸［J］.数学通讯，2013(7/8)：86-88.

［4］耿道永.中学数学“有效备课”的探索［J］.数学通报，2006(9)：15-17.