构造局部不等式解决一类不等式问题

●宋红军 (富阳中学 浙江富阳 311400) ●杨樟松 (衢州市第二中学 浙江衢州 324000)

构造局部不等式解决一类不等式问题

●宋红军 (富阳中学 浙江富阳 311400) ●杨樟松 (衢州市第二中学 浙江衢州 324000)

不等式问题是中学数学代数问题的基础和重点，在解决有些不等式问题时，特别是一些分式不等式和根式不等式，从整体上考虑往往难以下手，可以构造若干个结构完全相同的局部不等式来解决，只要局部不等式构造好了，解决这些不等式问题就方便得多了.下面结合一些具体例题谈谈如何利用局部不等式来解决问题.

首先看2个三元分式不等式问题，构造局部不等式来解决这类问题非常有效，当局部不等式构造得好时，既简化计算又简捷明了.

分析这类三元分式不等式看起来很简单，通常都是构造局部不等式来证明.思考此类问题时，总是想着将右边的常数也写成3个分式之和的形式，且相应的每个分式比左边的小，则问题就解决了.

例2设非负实数x，y，z满足条件：x2+y2+z2=1，求代数式的取值范围.

分析 这是一道IMO预选题的改编题，通常是在边界点或是相等时取到取值范围的最值，因此答案容易找到，但具体证明不太容易.初看可进行三角变换来计算，若真这么做，计算量可就大了，原题解答是通过函数分析来计算的，也不容易.笔者发现通过找局部不等式来解答比较容易.

在处理根式不等式时，通常不能直接平方，从而计算量非常大.如果能找到局部不等式来处理，那么就简单多了.下面结合几个具体例题来看局部不等式在含根式不等式中的应用.

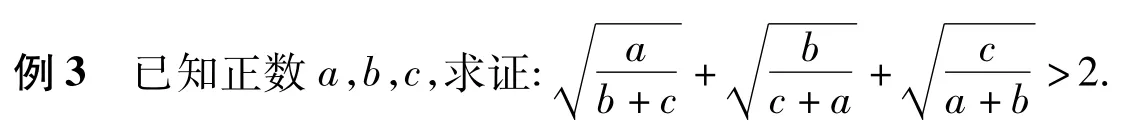
分析对于这种类型的不等式，根据经验常通过局部不等式进行证明，该题的局部不等式比较容易找到.

构造局部不等式证明不等式问题是一种常见的技巧，它常常能解决琴生不等式解决不了的问题，笔者希望本文能给读者带来一些启发.