点运动的路径长问题

●金 岭 (湖州市第四中学教育集团 浙江湖州 313000)

点运动的路径长问题

●金 岭 (湖州市第四中学教育集团 浙江湖州 313000)

近年来，各地中考试题中不断出现有关求点运动的路径长问题，隐含了解析几何“求点的运动轨迹方程”的雏形.这类题目中，条件点随整个几何图形的运动而运动，其背景模糊，轨迹不明，计算繁杂，造成学生的解题思路受阻.而命题者常将其设计成填空、选择、解答题中的压轴题，显得极为重要.从动点所经过的路径来分类，常见的有线段和圆弧，本文拟通过典型中考试题加以解析，从中探究这类试题的解题思路.

1 线段型

例1如图1，已知点A是第一象限内横坐标为的一个定点，AC⊥x轴于点M，交直线y=－x于点 N.若点 P是线段 ON上的一个动点，∠APB=30°，BA⊥PA，当点 P在线段 ON上运动时，点A不变，点B随之运动，求点P从点O运动到点N时，点B 运动的路径长是＿＿ .

(2013年浙江省湖州市数学中考试题)

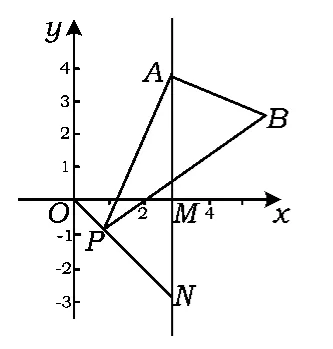
图1

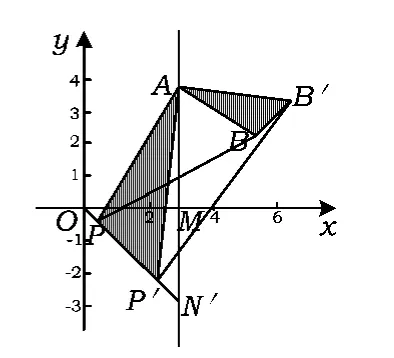
图2

例2在矩形ABCD中，点P在AD上，AB=2，AP=1.将直角尺的顶点放在P处，直角尺的2边分别交AB，BC于点E，F，联结EF(如图3).

(1)当点E与点B重合时，点F恰好与点C重合(如图4)，求PC的长.

(2)探究：将直尺从图4中的位置开始，绕点P顺时针旋转，当点E和点A重合时停止.在这个过程中，请你观察、猜想，并解答：①tan∠PEF的值是否发生变化?请说明理由;②直接写出从开始到停止，线段EF的中点经过的路线长.

(2011年福建省三明市数学中考试题)

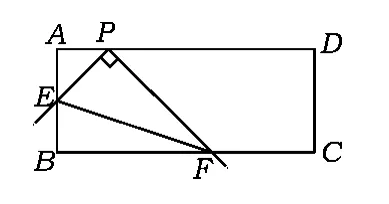
图3

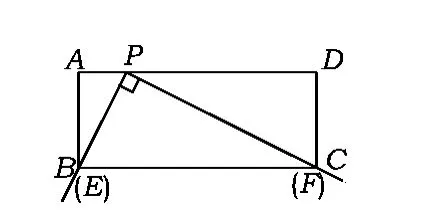
图4

(2)①tan∠PEF的值不变.

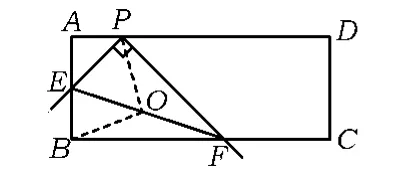
图5

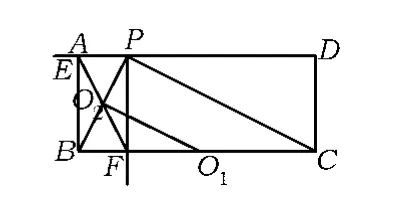
图6

例3如图7，正方形ABCD的边长是2，M是AD的中点，点E从点A出发，沿AB运动到点B停止.联结EM并延长交射线CD于点F，过点M作EF的垂线交射线BC于点G，联结EG，FG.

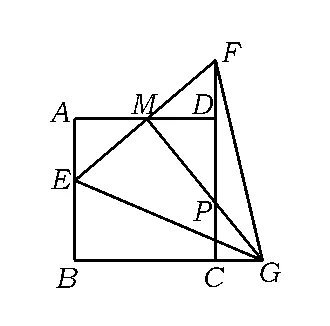
图7

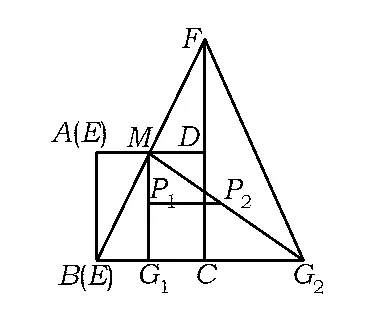
图8

(1)设AE=x时，△EGF的面积为y，求y关于x的函数关系式，并填写自变量x的取值范围.

(2)P是MG的中点，请直接写出点P运动路线的长.

(2010年江苏省南京市数学中考试题)

分析(1)y=2x2+2，其中0≤x≤2.

(2)如图8，分析知：当起始位置点E与点A重合时，BG1=AM=1;当终点位置点E与点B重合时，由△AMB∽△MBG2，知 BG2=5，G1G2=4，于是点P到BC的距离始终保持不变(为1)，故P1P2(P1是P的起始位置，P2是P的终止位置)是点P运动的路线，得P1P2=2.

点评点运动路径为线段类题型，可先寻找特殊位置(起点、终点)相对应的条件点所在的位置.再抓住图形的几何特征，运用图形的平移、旋转、翻折等变化，发现三角形的相似或全等等关系，找出运动之中的不变关系，从而知道运动轨迹的形状是一条线段，再计算获得解答.

2 圆弧型

例4如图9，以G(0，1)为圆心，半径为2的圆与x轴交于点A，B，与y轴交于点 C，D，点 E为⊙G上一动点，CF⊥AE于点F.当点E从点B出发逆时针运动到点C时，点F 所经过的路程长为＿＿.

分析(1)点E在起点B时，点F与点O重合;点E在终点C时，点F与点C重合.

(2)在点E的运动过程中∠CFA=90°始终不变，观察∠CFA所对的边为AC，得到点F在以AC为直径的圆P上(如图10)，点F形成的轨迹为

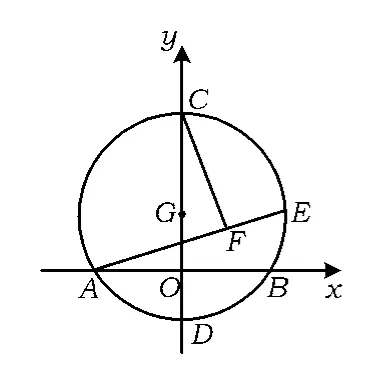
图9

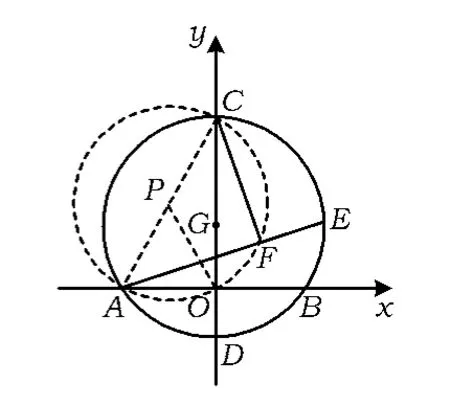
图10

例5如图11，已知正方形OABC的边长为2，顶点A，C分别在x，y轴的正半轴上，M是BC的中点.P(0，m)是线段OC上一个动点(点C除外)，直线PM交AB的延长线于点D.

(1)求点D的坐标(用含m的代数式表示);

(2)当△ADP是等腰三角形时，求m的值;

(3)设过点P，M，B的抛物线与x轴的正半轴交于点E，过点O作直线ME的垂线，垂足为H(如图12)，当点P从原点O向点C运动时，点H也随之运动，请直接写出点H所经过的路径长(不写解答过程).

(2011年浙江省湖州市数学中考试题)

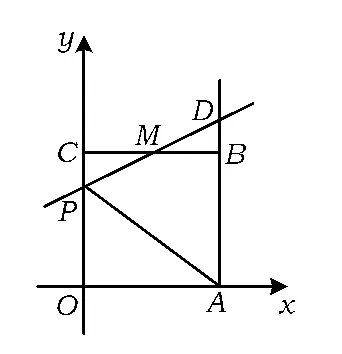
图11

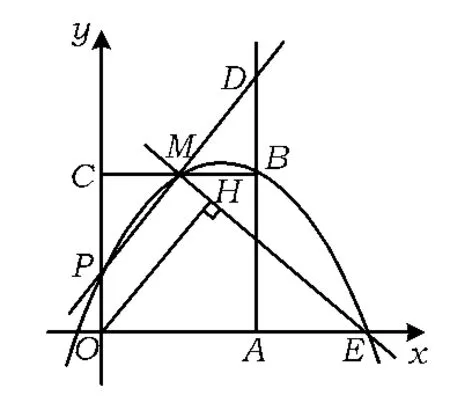
图12

分析(1)易得点D的坐标为(2，4－m).

(3)可先探求点H经过的路径是什么图形，通过观察发现“过点O作直线ME的垂线，垂足为H”，直角始终存在，直角∠OHM对应的斜边OM始终不变，这是运动之中的不变，因此点H在以OM为直径的圆 G上(如图13)，G是 OM的中点，再确定点H运动的起点和终点，可以发现当点P在点O时，H在运动的起点，此时易得∠COH=45°，则∠CGH=90°;当 H 接近点C时，H也无限接近点C，但不能达到点C.于是点H运动在以OM为直径、圆心角为90°的弧上，路径长为

点评当点运动路径为圆弧类题型时，也要先寻找特殊位置(起点、终点)相对应的条件点所在的位置;再抓住图形的几何特征，条件点往往是直角的顶点，在运动过程中对应一条斜边不变，这是运动中的不变关系，从而知道运动轨迹的形状是一条弧，再计算半径和圆心角获得解答.

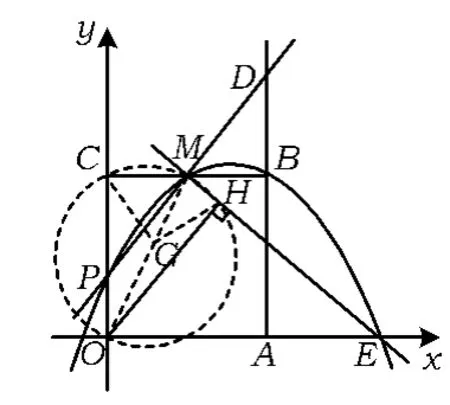
图13

结束语点运动的路径长问题是动态问题中的一种，也是近几年数学中考的热点，这类试题能很好地展示考生的分析、探究能力，考查数学综合素养，因而备受青睐.解决这类问题的关键：(1)分析起点和终点，找到特殊位置;(2)分清运动形成的轨迹是线段还是圆弧.