多间隙弯扭耦合齿轮非线性振动的分岔特性研究

盛冬平，朱如鹏，陆凤霞，靳广虎

（南京航空航天大学 江苏省精密与微细制造技术重点实验室，南京 210016）

齿轮传动系统具有传递功率大、转速高、工作条件苛刻，外形尺寸小、重量轻等特点，对传动系统的设计指标要求高，在航空、船舶、汽车、起重机械以及其他机械传动中获得了越来越广泛的应用，近年来吸引了国内外众多学者对其动力学特性进行了大量的研究［1－2］。王三民等［3］研究了在不同支承刚度下多间隙耦合的非线性圆柱直齿模型进入混沌的途径以及在增大支承间隙时系统发生跳跃和失稳现象，但没有进一步分析转速和齿侧间隙对分岔和混沌动力学特性的影响。王三民等［4］还研究了含摩擦和间隙的直齿轮副的分岔和混沌特性，包括在一定的参数下，摩擦能使混沌吸引子转变为周期吸引子同时可以使系统提前进入混沌。李同杰等［5］研究了行星齿轮纯扭转系统在不同转速和不同阻尼下的非线性振动的混沌及分叉特性，以及在两种不同参数的情况下系统由稳定振动进入混沌和回归周期一的不同道路。孙智民等［6］研究了带有间隙的星形齿轮传动扭转振动系统在改变系统激振频率的情况下，通往混沌的道路有周期倍化道路和拟周期道路，同时还研究了系统在不同的阻尼情况下，系统也会由周期倍化道路或者拟周期道路通往混沌。然而，从目前可以检索到的文献来看，关于齿轮多间隙弯扭耦合非线性振动系统在不同转速、不同啮合阻尼、不同支承间隙以及不同齿侧间隙下的分叉特性的研究尚鲜有报道。

本文建立在文献［3］的基础上综合考虑齿轮传动系统中齿轮副间的时变啮合刚度、齿侧间隙、支承间隙以及综合传递误差等非线性因素，以圆柱齿轮传动的齿轮－转子－轴承为研究对象，建立了多间隙的弯扭耦合的非线性振动模型，并采用数值积分方法研究了齿轮的弯扭振动特性随转速、齿侧间隙、支承间隙以及啮合阻尼系数等分岔参数的变化情况，通过对仿真结果的分析，获得一些理论结果。

1 多间隙弯扭耦合振动模型

多间隙弯扭耦合振动系统由一对齿轮副，轴和轴承组成，此处设定各齿轮为圆柱直齿齿轮，且不考虑齿轮副之间的摩擦力，系统的考虑各种误差和多间隙弯扭振动模型如图1所示。

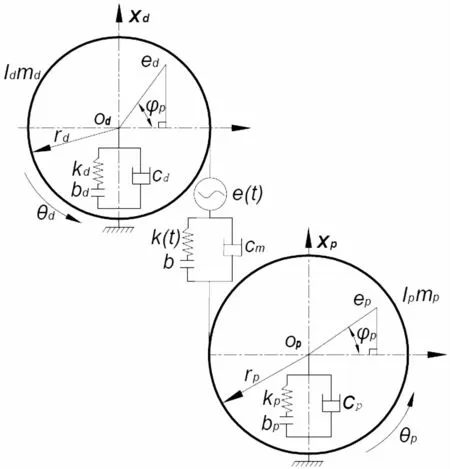
图1 多间隙弯扭耦合齿轮振动系统模型Fig．1 Transverse-torsional coupled gear vibration system with multiple-clearances model

图1中，主动轮和从动轮的角位移分别用θd和θp表示，基圆半径分别用rd和rp表示。主动轮支承轴承的刚度、半支承间隙、阻尼分别用kd、bd、cd表示。从动轮支承轴承的刚度、半支承间隙、阻尼分别用kp、bp、cp表示，齿轮啮合副间的综合啮合误差、时变粘合刚度、半齿侧间隙、啮合阻尼分别用 e（t）、k（t）、b、cm表示。ed和ep为主动轮和从动轮的偏心误差。φd和φp为主动轮和从动轮偏心误差的初始相位。主动轮和被动轮在相应的啮合线上产生的线位移xd和xp可以表述如下

根据直齿齿轮啮合副刚度变化特点，将其假定为矩形波变化规律。图2显示了齿轮副传动时啮合刚度的变化规律。

图2 齿轮副啮合时变刚度Fig．2 Time-varying meshing stiffness

图2中，kmax为啮合时变刚度的最大值，kmin为啮合时变刚度的最小值，φ为啮合刚度变化的初相位，T位啮合周期，T＝2π／ω，ω为啮频。

周期矩形波可以展开成为以啮频为基频的Fourier级数，取一次谐波项为

式中，km为啮合副上的平均啮合刚度，ka为啮合副上的刚度变化幅值。

该系统具有四个自由度，其广义坐标可以表示为（θd，Xd，θp，Xp）T，其中，θd和 Xd为主动轮的转动自由度和纵向位移自由度，θp和Xp为从动轮的转动自由度和纵向位移自由度。

1.1 间隙非线性函数和动态啮合力

对于单对外啮合的齿轮副来说，其啮合点的相对位移Xr和误差e（t）的表达式为

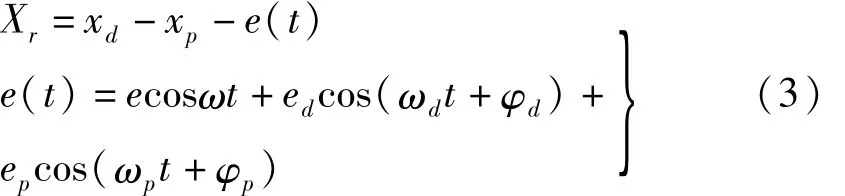
式中，e（t）为主动轮和从动轮的静态误差以及啮合误差在啮合线上的投影。

齿轮系统间隙非线性函数可以表示为

齿轮啮合副上的动态啮合力为弹性恢复力和阻尼力之和，可以表示为

式中，阻尼系数的表达式为

式中，ξ为啮合副相对阻尼比，md为主动轮质量，mp为从动轮质量

1.2 系统的振动微分方程

1．2．1 系统的弯扭振动方程

规定输入转矩作用下各个主、从动轮的运动方向为各自角位移相应的正方向。取 θd、Xd、θp、Xp为广义坐标。根据刚体定轴转动微分方程，图1所示系统在输入转矩Td及负载Tp作用下，可列出弯扭耦合振动微分方程为

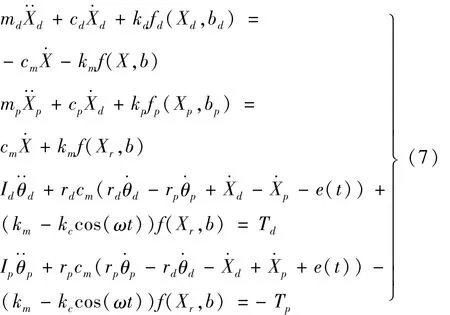
1．2．2 系统相对坐标下的弯扭振动方程

由于齿侧间隙的存在，使得齿轮传动系统约束不完整，从而决定了式（7）为半正定系统，存在刚体位移及不定解。为了消除刚体位移，并保持系统拓扑解结构不变的前提下，利用同胚映射，实现方程个数的减少，从而实现降维，以便于研究系统的分岔特性，同时利用（1）式，引入相对坐标

式中，X为啮合线上相对位移的叠加，与xd，xp有相同的分岔特性。将式（7）变形后得到

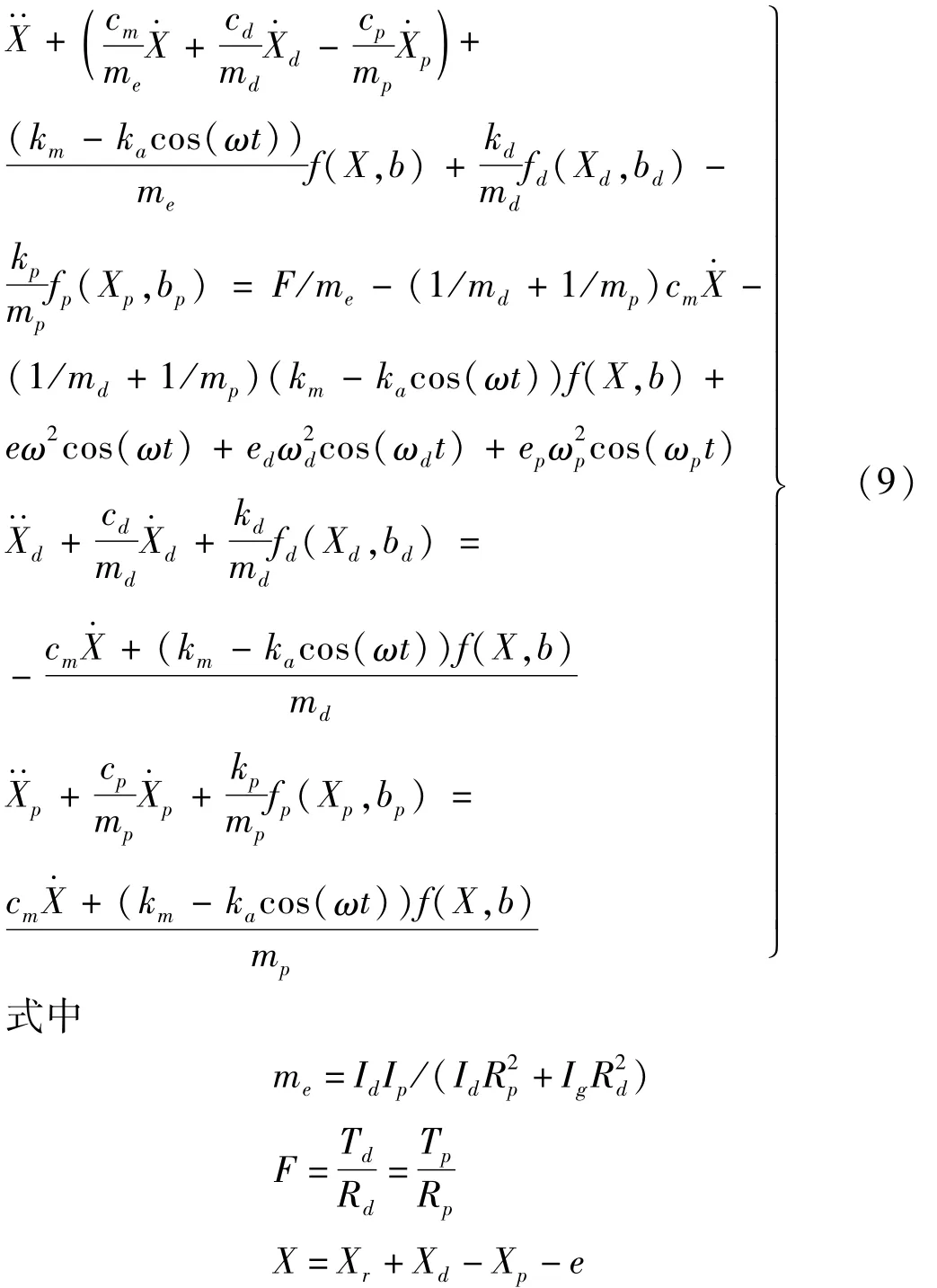
1．2．3 系统的量纲一方程

引入 量纲一时间 τ＝ωnt，其中 ωn为啮合刚度均值，引入位移标称尺度bc，则量纲一位移，速度，加速度表示为 X量纲一转速

量纲一间隙非线性函数为

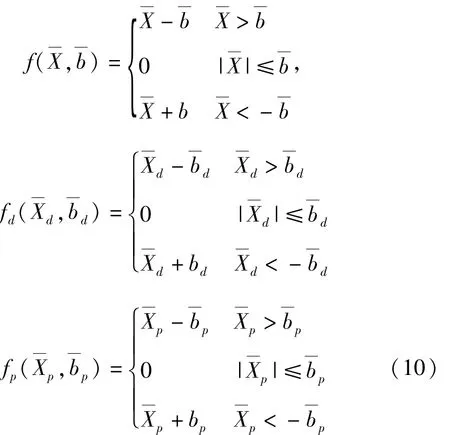
将以上各式带入式（9）中，变形整理后可得到系统的矩阵形式的量纲一化方程为

2 运动的分岔特性分析

为了进行多间隙齿轮传动系统的运动分岔特性研究，本文取系统的一组基本计算参数：模数m＝3 mm，α＝20°，zd＝40，zp＝80，ed＝10μm，ep＝10μm，bc＝10μm，bd＝10μm，bp＝10μm，kd＝0．2 GN／m，kp＝0．35 GN／m，输入功率P＝200 kW。

采用变步长的4阶Runge-Kutta法求解量纲一式（11），用所求的的数值解分别得到了系统在不同参数下的分岔图和Poincaré截面图，并据此为工具研究系统的运动分岔特性。

2.1 系统随量纲一转速Ω变化的分岔特性

取系统中啮合副的半齿侧间隙b＝60μm，研究系统的啮合副相对阻尼比分别取0．05，0．07，0．09和0．11下的方程的解随量纲一转速Ω的分岔特性如图3所示。

图3展示了系统运动随转速变化而表现出的多样的分岔特性。可以看出，系统在不同量纲一转速下经历了不同的运动状态，包括短周期运动和复杂运动形态（长周期运动、拟周期和混沌运动）之间的分岔，最终系统稳定于周期一运动。由于实际运动的复杂性，系统的工作转速可能位于以上某一分岔点对应的转速附近，而实际工作转速的微幅变化可能会使得系统由稳态运动进入不稳定运动，而这种不稳定运动会导致齿轮啮合副产生强非线性的单边冲击或者双边冲击现象，从而导致齿根承受除了由于刚度变化导致冲击以外的冲击载荷，进而降低齿轮的疲劳寿命，同时这种不稳定运动会使系统产生多频甚至混沌的噪音，从而影响工作环境的舒适性。

随着相对阻尼比的增加，系统的混沌区间宽度逐渐减小，由图3（d）可以看出当啮合副的相对阻尼比ξ＝0．11时，只存在长周期运动和短周期运动。当ξ＝0．13时，系统只存在周期一的稳定运动。另外，可以看出随着阻尼比的增加，系统由周期二运动进入周期一运动的分叉点的量纲一转速逐渐降低，图3（a）～3（d）的分岔临界点量纲一转速分别为 1．72，1．66，1．54，1．49。

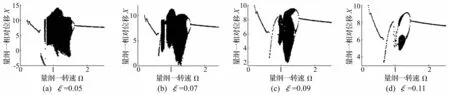
图3 系统在不同阻尼比下随Ω变化的分岔图Fig．3 Bifurcation map with the increase of rotation speed under different meshing damp ratio

图4显示了系统间隙为60μm，相对阻尼比为0．07，量纲一转速从0．75向0．9变化时系统由混沌运动历经拟周期运动，经过不稳定的吸引子后，再次通过拟周期进入混沌的全过程。从图4（a）和4（h）的Poincaré截面图中的内部自相似的分形结构可以判断系统正处于混沌运动状态。图4（b）～4（h）显示了系统在进入混沌过程中不稳定吸引子随着分岔参数而呈现的6种形态。

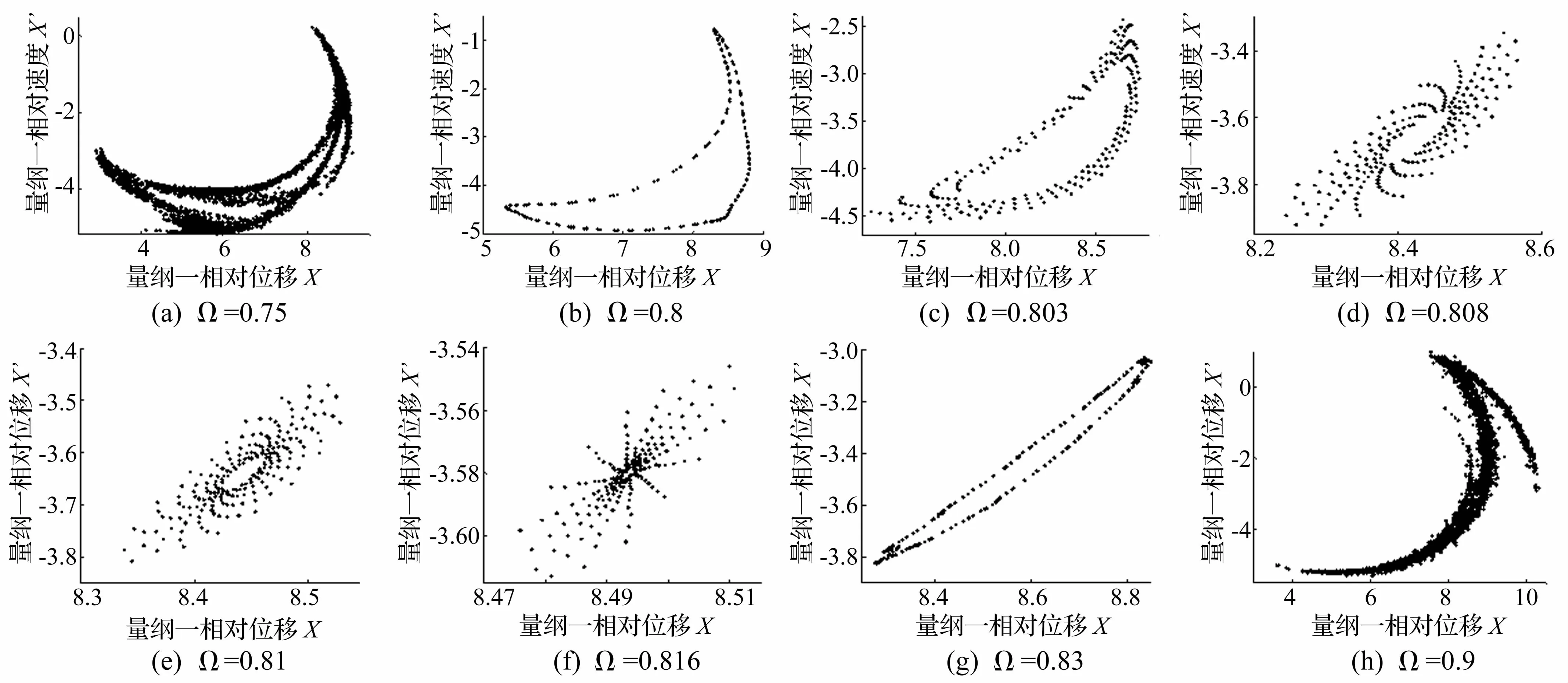
图4 系统在不同量纲一转速下的Poincaré图Fig．4Poincarémap with the increase of rotation speed under different meshing damp ratio

综合从图3和图4可以看出，系统从周期一的稳定运动通过拟周期通道进入混沌的临界点位于系统的一阶临界转速附近，且随着啮合相对阻尼比的增加，该临界点逐渐趋近于一阶固有频率下的转速，在当前系统参数下，此时该系统的一阶临界转速为6 837 r／min。

从图机械系统中的混沌意味着系统的运动不再具有可控性和可预测性，它总是不断从某个运动轨道突跳到另外一个运动轨道上去，对于机械系统来说，这就意味着疲劳寿命的降低和噪音的增加。通过以上转速全局分岔图以及Poincaré图进行定性和定量分析，可以获得混沌运动和多周期运动的转速区域和临界值，从而可以人为控制和避开不可控和不可预测性的运动。

2.2 系统随量纲一齿侧间隙变化的分岔特性

取系统量纲一转速Ω＝1．2，啮合副相对阻尼比分别0．05、0．07、0．09和 0．11，方程的量纲一位移 X随系统量纲一齿侧间隙变化的分岔特性如图5所示。可以看出当系统在不同阻尼比下的具有不同分岔特性。图5（a）和5（b）显示系统通过激变的途径进入混沌，且随着间隙的增加一直处于混沌运动中。图5（c）显示系统通过激变进入混沌后，在一定宽度混沌运动后，经由倒分岔进入并锁相为周期四运动。图5（d）显示了系统通过倍周期分岔进入混沌，又经过倒分岔进入周期二的短周期运动。纵观整个变化过程，可以发现系统随着阻尼比的增加，运动进入混沌的途径由激变转变为倍周期分岔，并且存在一个转变临界值。更多的计算表明，系统随着转速或相对阻尼比的增加，运动不再具有混沌和分岔特性，整个运动区域为周期一的稳定运动。

图6显示了系统取量纲一转速为Ω＝1．2，啮合相对阻尼比ξ＝0．11，方程的量纲一位移X随量纲一间隙变化的分岔特性和b＝60μm时的Poincaré图。图6（a）显示了系统经过周期一运动通过倍周期分岔进入一定位移宽度的运动，而图6（b）则证明系统经过倍周期分岔后又经过Naimark-sacker分岔形成两个不变吸引圈。

图5 系统在不同啮合阻尼比下随量纲一间隙变化的分岔图Fig．5 Bifurcationmap with the increase of the backlash under different meshing damp ratio

图6 系统在ξ＝0．11的分岔图和b＝60μm的 Poincaré图Fig．6 Bifurcationmap with the increase of the backlash（ξ＝0．11）and the Poincarémap（b＝60μm）

2．3 系统随量纲一支承间隙变化的分岔特性

从系统的控制方程可知，系统存在阻尼耦合和弹性耦合。取系统量纲一转速Ω＝1．2，量纲一啮合间隙b＝30μm，啮合副相对阻尼比分别 0．05、0．06、0．07和0．08，方程的量纲一位移X随系统量纲一支承间隙变化的分岔特性如图7所示。可以看出当相对阻尼比为0．05时，支承间隙在b＝30μm附近出现狭窄的周期五窗口，且从位移解值可以看出系统支承间隙对系统在啮合线上的运动的影响较弱，且随着啮合阻尼的增加，耦合作用的影响也逐渐被抑制，且只有在少数且不连续的支承间隙下对系统有一定的扰动。

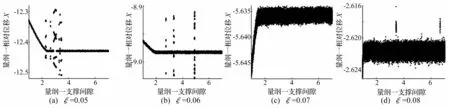
图7 不同阻尼比下随量纲一支承间隙变化的分岔图Fig．7 Bifurcationmap with the increase of gear support clearance under different meshing damp ratio

3 结 论

（1）多间隙弯扭耦合齿轮传动系统在各种非线性因素的综合影响下表现出了丰富的分岔特性，随着分岔参数的变化先后出现了短周期运动、长周期运动、拟周期运动和混沌运动。

（2）随着转速的增加，系统会通过激变途径进入到混沌运动，然后又通过倒分岔进入拟周期运动，经过一定宽度的吸引域窗口后通过拟周期再次进入混沌运动，最终通过倒分岔回归周期一运动。

（3）啮合阻尼系数的变化对于系统运动的分岔特性有较明显的影响。随着阻尼系数的增加，混沌运动的宽度逐渐较小，最终转变为整个量纲一转速上的周期一运动。

（4）齿侧间隙也是影响系统运动分岔特性的重要因素。但其影响范围主要集中在量纲一间隙大于3的大间隙和低转速范围内。在一定的转速下，随着啮合阻尼的增大，进入混沌的途径也由激变转变成倍周期分岔，且通过混沌区域后最终锁相为周期四、周期二或周期一运动。

（5）在满足一定的参数条件下，系统会随着齿侧间隙的增加由倍周期分岔进入并锁相为Naimark-sacker分岔。

（6）在一定的条件下，系统运动会随着支承间隙的增加进入狭窄的周期五窗口后锁相为周期一运动，从系统的控制方程和数值解可以发现系统的支承间隙对系统的运动影响较弱。

［1］Zhu Fu-min，Li Wan-li，Maropoulos PG．Tolerance analysis of a planetary gear reducer under cad circumstance［J］．Chinese Journal of Mechanical Engineering，2005，18（3）：342－345．

［2］Sun Dong-ye，Qin Da-tong，Wang Hong-yan．Control strategy of a parallel hybrid car with a metal belt-planetary gear continuously variable transmission system［J］．Chinese Journal of Mechanical Engineering，2002，15（3）：199－203．

［3］王三民，沈允文，董海军．多间隙耦合非线性动力系统的分叉与混沌［J］．西北工业大学学报，2003，21（2）：191－194．WANG San-min，SHEN Yun-wen，DONG Hai-jun．Bifurcation and chaos in a nonlinear dynamic with multiple clearances and time-varying stiffness［J］．Journey of Northwestern Polytechnic University，2003，21（2）：191－194．

［4］王三民，沈允文，董海军．含摩擦和间隙直齿轮副的混沌与分叉研究［J］．机械工程学报，2002，38（9）：8－11．WANG San-min，SHEN Yun-wen，DONG Hai-jun．Chaos and bifurcation analysis of a spur gear pair with combine friction and clearance［J］．Chinese Journal of Mechanical Engineering，2002，38（9）：8－11．

［5］李同杰，朱如鹏，鲍和云．行星齿轮扭转非线性振动建模与分岔特性研究［J］．机械工程学报，2011，47（21）：76－83．LI Tong-jie，ZHU Ru-peng，BAOHe-yun．Nonlinear torsion-al vibration modeling and bifurcation characteristic study of a planetary gear train［J］．Chinese Journal of Mechanical Engineering，2011，47（21）：76－83．

［6］孙智民，沈允文，王三民，等．星形齿轮传动系统分岔与混沌的研究［J］．机械工程学报，2001，37（12）：11－15．SUN Zhi-ming，SHEN Yun-wen，WANG San-ming，et al．Bifurcation and chaos of star gear system［J］．Chinese Journal of Mechanical Engineering，2001，37（12）：11－15．

［7］Ahmadian M，DeGuilio A P．Recent advances in the use of piezoceramics for vibration suppression［J］．Shock and Vibration Digest，2001，33（1）：15－22．

［8］Gu H C，Song G B．Active vibration suppression of a flexible beam with piezoceramic patches using robust model reference control［J］．Smart Materials and Structures，2007，16（4）：1453－1459．

［9］Lamarque CH，Bastien J．Numerical study of a forced pendulum with friction［J］．Nonlinear Dynamics，2000，23（4）：335－352．

［10］di Bernardo M，Kowalczyk P，Nordmark A．Bifurcations of dynamical systems with sliding：derivation of normal form mapping［J］．Phys D，2002，170（3－4）：175－205．

［11］Louroza M A，Roitman N，Magluta C．Vibration reduction using passive absorption system with Coulomb damping［J］．Mechanical Systems and Signal Processing，2005，19（3）：537－549．

［12］Chen Y，Zimcik D G，Wickramasinghe V K，et al．Research of an active tunable vibration absorber for helicopter vibration control［J］．Chinese Journal of Aeronautics，2003，16（4）：203－211．

［13］Wickramasinghe V K，Zimcik D G，Chen Y，et al．Smart Spring-An actively tunable vibration absorber designed to control aeroelastic response［J］．Structural Dynamics and Materials Conference，2003，5：3651－3658．

［14］Chen Y，Wickramasinghe V K，Zimcik D G．A novel smart spring concept for helicopter blade vibration and noise suppression［J］．Materials Science Forum，2005，475－479（3）：2095－2098．

［15］Chen Y，Wickramasinghe V K，Zimcik D G．Smart spring impedance control algorithm for helicopter blade harmonic vibration suppression［J］．Journal of Vibration and Control，2005，11（4）：543－560．

［16］Chen Y，Wickramasinghe V K，Zimcik D G．Experimental evaluation of the smart spring for helicopter vibration suppression through blade root impedance control［J］．Smart Materials and Structures，2005，14（5）：1066－1074．

［17］Wickramasinghe V K，Chen Y，Zimzik D G．Experimental evaluation of the smart spring impedance control approach for adaptive vibration suppression［J］．Journal of Intelligent Material Systems and Structures，2008，19（2）：171－179．

［18］Cavalini A A，Galavotti T V，Morais T S，et al．Vibration attenuation in rotating machines using smart spring mechanism［J］． Mathematical Problems in Engineering， 2011：328－336．