汽车驱动轮与从动轮胎面自激振动对比研究

左曙光，张浩鹏，赵愿玲，吴旭东，倪天心

（同济大学 新能源汽车工程中心，上海 201804）

轮胎非正常磨损现象广泛存在于高速行驶的汽车上，它会导致汽车过早更换轮胎，严重影响轮胎的寿命［1］。而多边形磨损是轮胎多边形磨损是指轮胎周向上形成多边形形状的磨损，其实质是轮胎非正常磨损的一种。这种多边形磨损可能导致轮胎提前报废，造成爆胎等严重威胁行驶安全的事故［2］。

AtsuoSueoka等［3－4］结合试验对汽车轮胎的多边形磨损进行分析，得出了轮胎多边形磨损的产生是由于垂直方向上由第一阶自由振动模态引起的结论。同济大学对从动轮多边形磨损机理进行了深入的研究［5］，指出轮胎多边形磨损是一种典型的非线性自激振动，且为一定的车速范围内轮胎会出现的“硬自激”振动；轮胎胎面侧向自激振动是多边形磨损的必要条件，当胎面的侧向自激振动频率与车轮滚动频率的商近似为整数时，轮胎才有可能形成多边形磨损，也通过影响因素分析支持了多个多边形磨损的特征［6－9］。但之前的工作主要研究从动轮上的自激振动和多边形磨损，没有解释“轮胎多边形磨损发生在从动轮的轮胎上，而较少发生在驱动轮的轮胎上”这一现象。在驱动轮上，由于接地特性以及轮胎与悬架的力学特性不同，进而导致驱动轮上产生自激振动和多边形磨损状况的不同，因此有必要对驱动轮的自激振动进行研究。

本文考虑驱动力对胎面侧向自激振动的影响，建立驱动轮悬架－胎面－路面系统的动力学模型，理论角度分析纵向力对自激振动系统的影响，并与从动轮对比，比较垂向载荷、胎压和前束角对自激振动的影响。

表1 文中符号代表的物理量Tab．1 The quantity of symbols

1 驱动轮悬架－轮胎－胎面五自由度系统模型的建立

根据某问题车辆采用的扭转梁式悬架，建立了驱动轮悬架－轮胎四自由度模型［10］，基于同样的假设前提，通过进一步考虑胎面纵向受力，在原有模型基础上建立驱动轮悬架－轮胎－胎面五自由度模型［11］，等效模型如图1所示。

图1 驱动轮悬架－轮胎－胎面五自由度系统Fig．1 Driving wheel suspension-tire tread five degree of freedom system

需要指出的是，本模型对原模型的改进主要体现为：胎面质量块与轮胎之间用三个带阻尼的线性弹簧相连。三个弹簧的方向分别始终沿着大地坐标系的X轴、Y轴、Z轴方向，分别代表胎面质量块与轮胎之间的纵向、侧向、垂向作用力关系，反映轮胎橡胶材料的在纵向、侧向以及轮胎充气部分的弹性特性。胎面质量块与地面始终保持接触，并且仅在沿轮胎侧向和纵向方向上有两个平移自由度，没有转动自由度。来自路面的摩擦力直接作用在胎面质量块上，并通过胎面质量块与轮胎之间的弹簧连接传递到后桥刚体，从而影响整个系统的运动情况。最终得到五自由度系统动力学微分方程组：

模型中各符号含义如表1所示。驱动轮－悬架模型与从动轮－悬架模型的主要区别，体现在胎面质量块与纵向力和侧向力的关系［11］。

图2 侧向力随纵向力变化情况Fig．2 Lateral force changing with longitudinal force

计算轮胎在纯侧偏或驱动工况下的侧向力，并与LuGre摩擦模型［12］结合来考虑轮胎侧向自激振动。得到不同侧偏角下的纵向力与侧向力的关系，其侧向力与纵向力关系如图2所示。

2 基于模型仿真的胎面自激振动分析机理分析

根据上述理论模型开展了不同车速下的驱动轮和从动轮的仿真计算，其产生硬激励自激振动的车速范围如图3所示。

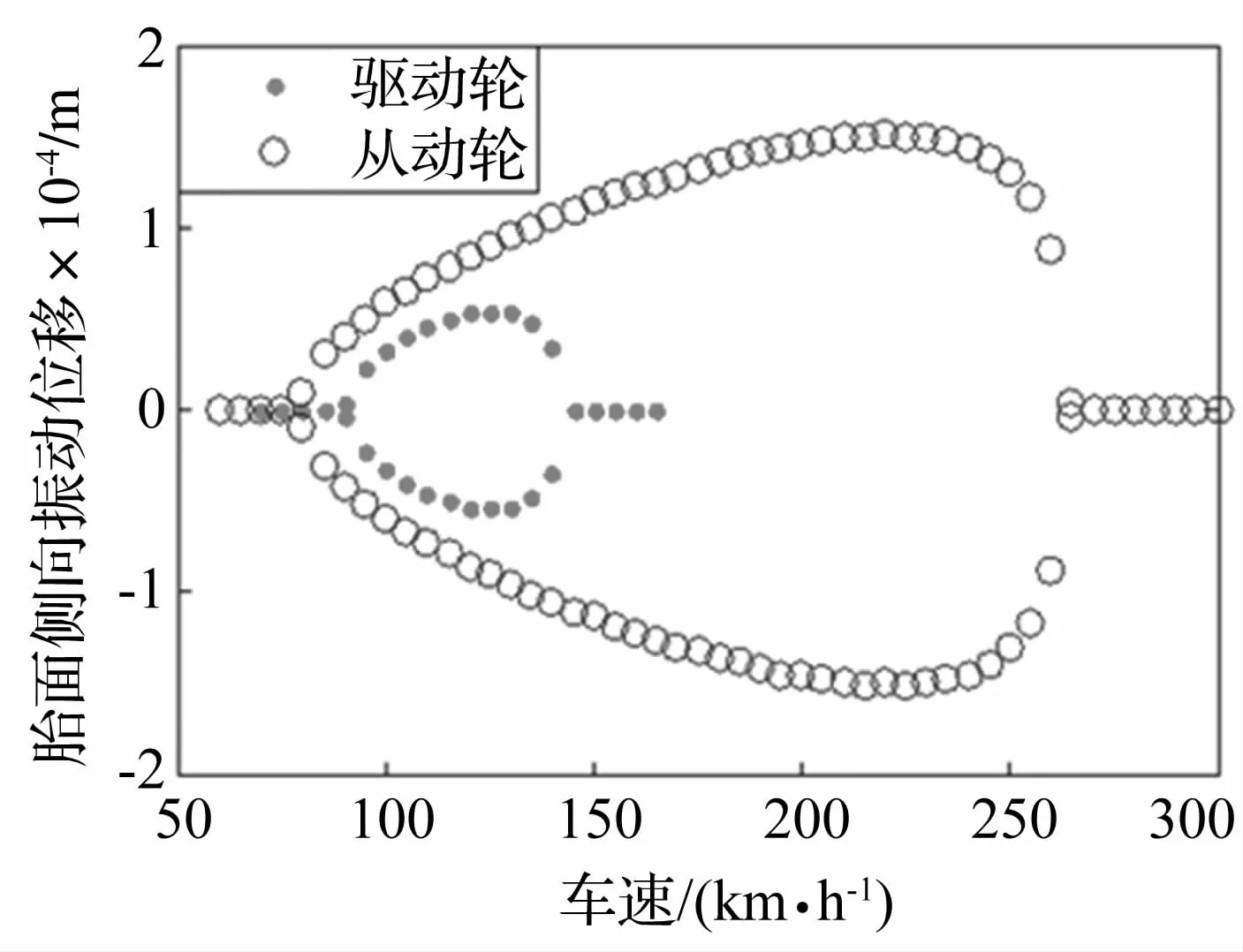
图3 侧向振动位移随车速变化的分岔图Fig．3 Bifurcation diagram how lateral vibration displacement changes with the speed

从图3中可知：驱动轮产生自激振动的车速范围远小于从动轮；而且驱动轮自激振动的位移幅值也小，说明产生自激振动的能量要比从动轮弱很多。为了进一步分析胎面质量块的侧向振动情况，从而解释图3的现象，将驱动轮和从动轮悬架－轮胎－胎面振动系统模型侧向力方程展开，得到其侧向振动的方程，驱动轮侧向振动方程如下（模型中各符号含义如表1所示）：

从动轮侧向振动方程如下：

在式（5）和式（6）中，Fric＿xzsinα和 f（α，β，γ，y）与侧向振动x和x·无关，在一段时间后会由于系统本身的阻尼衰减。而在驱动轮胎面侧向自激振动的模型中，系统当量阻尼由C3sin2α＋C2cos2α和摩擦特性曲线中的负斜率部分组成。车轮前束角α的变化量在模型中为一个很小的变量，接近于零。所以在从动轮和驱动轮的振动方程中：

两者均接近于系统固有阻尼C2，由从动轮和驱动轮的侧向振动方程可以看出，两者的振动阻尼变化并不大；导致从动轮和驱动轮系统当量阻尼差别的主要在LuGre摩擦模型［11］中的摩擦力特性曲线负斜率部分，如下式所示：

在LuGre摩擦模型中，决定摩擦特性曲线负斜率的主要有两组因素：stribeck指数α和stribeck速度vs，以及最大静摩擦力和滑动摩擦力的差值Fs－Fm。stribeck指数α和stribeck速度vs作为系统参数，以上参数由课题组前期识别［2］得来，且不能反映从动轮和驱动轮的差别，在此不对其进行讨论。由图4可知，Fs与Fm的差值越大，LuGre摩擦模型的负斜率绝对值越大，系统也就越容易表现出整体负阻尼状态，产生自激振动的可能性也增大。

图4 稳态LuGre摩擦模型负斜率变化Fig．4 Negative slope change in steady LuGre friction model

在驱动轮上，随着车速的增加，切向驱动力（驱动转矩）的增大，滑移率S绝对值增大，侧向摩擦力减小，在胎面侧向上的振动能量减小，同时胎面侧向上Fs与Fm差值减小，导致摩擦力特性曲线负斜率绝对值减小，胎面侧向振动当量阻尼增大，使得驱动轮产生自激振动的可能性下降。

由式（10）可知，当滑移率为0时，即在从动轮上，Fm与Fs的差值最大，也就是LuGre摩擦力曲线的负斜率绝对值最大，在同样的情况下，从动轮产生自激振动的可能性比较大。

3 参数影响分析

由实际现象与相关文献［1，2］可知，垂向载荷、胎压、前束角对胎面自激振动有影响，因此从以下三个影响因素进行分析。

3.1 垂向载荷对胎面自激振动的影响

垂向载荷增加、胎压降低会使轮胎的下沉量增大，接地印记的长和宽也会随着轮胎下沉量增大而增大，从而影响到接地质量块的质量和其表观刚度，并且垂向载荷对接地区间内的纵向、侧向的摩擦力也会有很大的影响，进而对胎面的自激振动造成影响。

根据文献［8］中对胎面等效刚度和质量的计算公式可知，随着垂向载荷的增加，轮胎下沉量增大，接地面积增加，侧向刚度和接地质量块质量随之变大，侧向振动频率正是与这两者的比值相关，胎面侧向振动频率的变化非常小，可以认为是不变的值。

图5 驱、从动轮随垂载变化的速度分岔图Fig．5 Bifurcation diagram how speed changes with vertical load in driving wheel and driven wheel

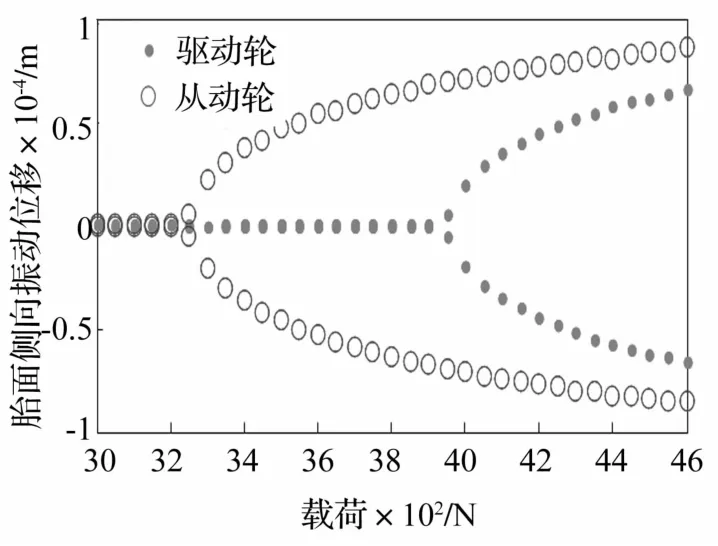
图6 车速120 km／h时驱、从动轮胎面侧向振动位移随垂载变化的分岔图Fig．6 Bifurcation diagram how lateral vibration displacement changes with vertical load at 120km／h in driving wheel and driven wheel

图7 驱、从动轮随胎压变化的速度分岔图Fig．7 Bifurcation diagram how speed changes with tire pressure in driving wheel and driven wheel

从图5中可知，在3 500 N垂向载荷下，驱动轮不产生自激振动。随着垂向载荷的增加，驱、从动轮产生自激振动的车速范围变大。同时，驱动轮与从动轮相比，要在更大的载荷范围内才能产生自激振动。从图6中可知，在常用车车速为120 km／h时，随着垂向载荷的增大，驱动轮和从动轮自激振动的能量均增大，驱动轮在载荷大于4 100 N时才能产生自激振动，从动轮在载荷大于3 300 N后就有可能产生自激振动。与从动轮相比，驱动轮的自激振动能量要小很多，且须在较大载荷下才能产生自激振动。汽车在载荷较大时，胎面产生自激振动的范围和能量均增大，即轮胎产生多边形磨损的几率也增加，为避免轮胎非均匀磨损的产生，汽车最好不要超载行驶。

3.2 胎压对胎面自激振动的影响

根据文献［8］中对胎面等效刚度和质量的计算公式可知，随着胎压的增大，轮胎整体垂向刚度变大，轮胎更不容易发生变形，因此接地面积减小，胎面侧向刚度也随之减小，轮胎接地质量减小，侧向振动频率正是与侧向刚度和接地质量的比值相关，胎面侧向振动频率的变化非常小，可以认为是不变的值。

从图7中可知，胎压越低，可以产生自激振动的车速范围越大，与从动轮相比，驱动轮产生自激振动的车速范围要小，且需要在更低的胎压下才会产生自激振动。从图8中可知，在车速为120 km／h时，驱动轮在胎压小于0．27 MPa时才能产生自激振动，从动轮在很大的范围内的胎压均有可能产生自激振动。在同一车速下，随着胎压的减小，驱动轮和从动轮自激振动的能量均增大，轮胎胎面侧向更易产生自激振动。这与车辆轮胎多边形磨损多发生在低压的情况下相符。与从动轮相比，驱动轮的自激振动能量要小很多，产生自激振动的胎压和车速范围比较小。汽车在低压下行驶，胎面产生自激振动的范围和能量均增大，及轮胎产生多边形磨损的几率也增加，为了避免轮胎非均匀磨损的产生，汽车最好不要在过低胎压下行驶。

3．3 前束角对胎面自激振动的影响

前束角是在轮胎的动力学仿真中非常重要的一个参数，随着前束角的增大，胎面越容易产生自激振动。

由图9可知，从动轮在前束角为0．19°时开始产生自激振动，驱动轮在前束角为0．3°产生自激振动。驱动轮和从动轮均在一定范围内的前束角下产生自激振动，同样的，驱动轮的自激振动参数范围比从动轮的小。实际上，车轮的前束角比较小，在0．2°左右，此时从动轮在一个较大的范围内产生自激振动，而驱动轮没有产生自激振动。

从图10中可知，在车速为120 km／h时，驱动轮在前束角为 0．25°～0．35°间可以产生自激振动，从动轮在前束角为0．2°～0．41°间能产生自激振动；与从动轮相比，驱动轮自激振动的最大能量约为从动轮最大能量的1／3，产生自激振动的前束角范围也较小，约为从动轮前束角范围的1／2。在一定的前束角范围内，随着前束角的增加，自激振动的能量也增加，所以在对前束角进行调整时，最好能避开这个范围。图10 车速120 km／h时驱动轮和从动轮胎面侧向振动位移随前束角变化的分岔图

图8 车速120 km／h时驱、从动轮胎面侧向振动位移随胎压变化的分岔图Fig．8 Bbifurcation diagram how lateral vibration displacement changes withtire pressure at 120 km／h in driving wheel and driven wheel

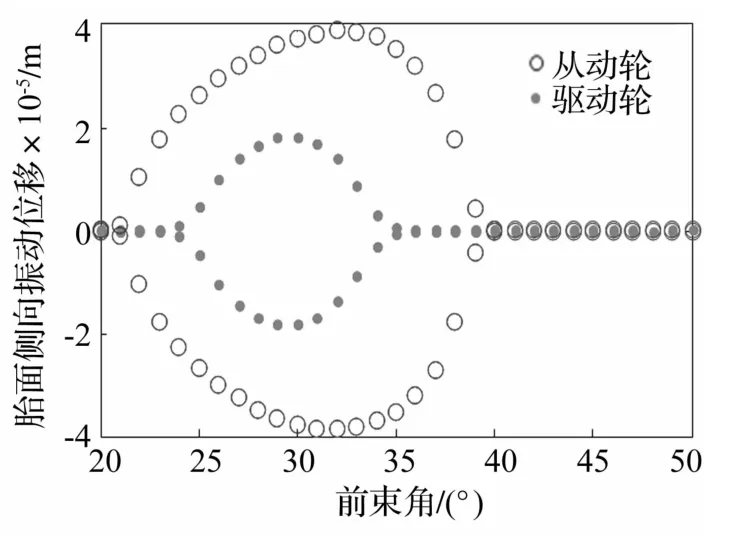
图10 车速120 km／h时驱动轮和从动轮胎面侧向振动位移随前束角变化的分岔图Fig．10 Bifurcation diagram how lateral vibration displacement changes with toe-in angle at 120 km／h in driving wheel and driven wheel

4 结 论

总体来说，驱动轮比从动轮产生胎面自激振动可能性和影响范围小。主要表现在以下几方面：

（1）与从动轮相比，驱动轮由于驱动力矩的增加，使得侧向可利用的附着力减小，从而导致侧向摩擦力曲线中的负斜率绝对值减小，侧向振动方程的当量阻尼增大，从而系统产生自激振动的可能性减小；

（2）驱动轮和从动轮自激振动情况随着胎压和载荷变化的趋势一致，都是在低压、高载的情况下容易产生自激振动；而在相同条件下，驱动轮产生自激振动的区间和能量较从动轮都要小很多。在车轮的行驶中，要尽量避免轮胎在低压和超载下工作，以免造成轮胎的非正常磨损，本文为此找到了理论依据；

（3）驱动轮和从动轮均在一定的前束角范围内产生自激振动，驱动轮的自激振动范围较从动轮要小很多。在常用的前束角范围内，从动轮在一个较大的车速范围内产生自激振动，驱动轮没有产生自激振动。

［1］杨宪武，左曙光，雷镭，等．基于胎面－路面摩擦自激的轮胎非线性振动建模仿真［J］．振动与冲击，2010，29（5）：211－214．YANG Xian-wu，ZUO Shu-guang，LEI Lei，et al．Modeling and simulation for nonlinear vibration of a tire based on friction self-excited［J］．Journal of Vibration and Shock，2010，29（5）：211－214．

［2］李勇，左曙光，雷镭，等．基于LuGre摩擦模型的轮胎多边形磨损机理分析［J］．振动与冲击．2010，29（9）：108－112．LI Yong， ZUO Shu-guang，LEI Lei， et al． Mechanism analysis of polygonal wear of tire based on LuGre friction model［J］．Journal of Vibration and Shock，2010，29（9）：108－112．

［3］Matsuzaki K，Sueoka A，Ryu T．Generation mechanism of polygonal wear of work rolls in a hot leveler and a countermeasure by dynamic absorbers［J］．International Journal of Machine Tools＆Manufacture．2008，48（9）：983－993．

［4］Sueoka A，Ryu T，Kondou T．Polygonal wear of automobile tire［J］．Jsme International Journal Series C-mechanical Systems Machine Elements and Manufacturing．1997，40（2）：209－217．

［5］黄铧，左曙光，杨宪武，等．基于LuGre摩擦模型的轮胎自振系统数值分析［J］．计算机辅助工程，2009，18（4）：19－23．HUANG Hua，ZUO Shu-guang，YANG Xian-wu， et al．Numerical analysis on self-excited vibration system of tire based on LuGre friction model［J］． Computer Aided Engineering，2009，18（4）：19－23．

［6］李勇，左曙光，雷镭，等．轮胎多边形磨损的产生条件及磨损边数研究［J］．计算力学学报，2011（3）：406－411．LI Yong， ZUO Shu-guang，LEI Lei， et al． Formation conditions and wear on the number of edges of polygonal wear of tire［J］．Chinese Journal of Computational Mechanics，2011（3）：406－411．

［7］汽车轮胎学，庄继德著［M］．北京：北京理工大学出版社，1997．

［8］杨宪武．轮胎多边形磨损中自激振动建模及关键参数研究［D］．上海：同济大学，2011．

［9］吴旭东．基于轮胎－悬架振动系统的轮胎多边形磨损研究［D］．上海：同济大学，2011．

［10］虞健，左曙光，陈栋华，等．扭转梁式半独立悬架建模与动态特性分析［J］．系统仿真学报，2006，18（8）：2300－2306．YU Jian，ZUO Shu-guang，CHEN Dong-hua，et al．Torsional beam type semi independent suspension modeling and dynamic characteristics analysis［J］．Journal of System Simulation，2006，18（8）：2300－2306．

［11］赵愿玲．驱动轮与从动轮胎面自激振动对比研究［D］．上海：同济大学，2013．

［12］Freidovich L，Robertsson A，Shiriaev R，et al．LuGre-Model-Based friction compensation［J］．IEEE Transactionson Control Systems Technology，2010，18（1）：194－200．