考虑河流冲刷作用的车桥耦合系统动力分析

李克冰，张 楠，方翔宇，田 园，夏 禾

（北京交通大学 土木建筑工程学院，北京 100044）

随着我国经济的发展，跨江大桥、超长跨海湾大桥的建设已经进入一个飞速发展的阶段。目前，高速铁路大规模兴建，其中高架桥梁的总里程占线路总长的比例非常高，这些桥梁中跨江跨海的也不在少数。许多桥梁不同程度地受到水流冲刷的影响。近年来出现一些因冲刷使桥梁发生倒塌的事故，给生命财产安全造成危害。2001年8月，蓝烟线外夹河桥和东莱线东泉河桥分别因桥渡冲刷而倒塌，因及时拦停了列车，未造成重大人员财产损失；2002年6月，西安灞河爆发洪水，将陇海线灞河桥1～5号桥墩冲垮，1～6孔梁坠落，造成陇海线双线中断行车14．5小时；2008年9月份，台湾南横公路高雄县甲仙乡甲仙大桥被湍急的旗山溪水冲击，桥墩松动，桥面陷落，无法通行而封桥。

水流冲刷对基础埋深的改变直接会对桥梁动力特性以及运行在桥上的列车的动力响应产生影响。因此，对在河流冲刷作用下的车桥系统动力响应及列车行车安全性的分析研究是必要的。

在进行河流冲刷对桥梁动力响应的影响研究时，首先要确定冲刷深度。目前，桥墩冲刷深度的计算主要有三类：基于冲深与来流强度关系的来流相关法，基于桥墩冲刷深度主要影响参数进行量纲分析的经验方法，还有解析法或者半经验法［1］。从国内外现行的冲刷深度计算公式看都是经验性的或半经验性的，目前尚未发现纯理论推导公式，大都采用实验资料来建立局部深度的关系式，然后用野外实桥观测资料来修正系数和指数得到冲刷深度计算公式［2］。

本文仅考虑冲刷作用对桥梁基础刚度的影响，并认为此类影响仍在线性范围内，因此有关车桥动力分析仍可以通用的方式进行。吴定俊等［3］以m法确定了基础弹性刚度，建立了考虑桩土相互作用的高速铁路桥梁－墩－基础体系列车过桥动力分析模型；蒋通等［4］将支架及支架下的桩基础和土体的弹性变形采用弹性支座模拟，研究了弹性支撑条件下对车－桥体系振动的影响；单德山等［5］以某铁路曲线多跨简支梁桥为例，将冻土区地面以下的地基土等效为线性弹簧，从而简单的考虑了桩土的相互作用效应；李小珍等［6］以等效地基刚度考虑桥梁桩土相互作用，分析了某主跨为1 120m的悬索桥的车桥动力性能。

河流冲刷可显著降低高速铁路桥梁基础埋深，有可能影响桥梁整体刚度，劣化其服役性能。因此本文进行了群桩基础的冲刷深度计算，建立了基于全过程迭代的列车－桥梁系统动力分析模型，通过考虑河流冲刷引起的群桩基础等效刚度变化，进行水流冲刷对车桥动力响应及行车安全性的影响研究。

1 桩基承台基础冲刷深度

对于架设桥梁的河道，除河床的自然演变外，还有桥梁孔径压缩水流和墩台阻挡水流引起的冲刷，各种冲刷交织在一起同时进行，冲刷过程较为复杂。根据泥沙运动和河床变形原理，桥墩附近的河床变形的原因可以分为三类：河道自然演变引起的河床变形，一般冲刷和局部冲刷。目前对冲刷深度的计算，一般先算出一般冲刷，再用一般冲刷后的水流条件计算局部冲刷，二者相加即为总冲刷深度。

总体来说，国内外对群桩基础局部冲刷的预测，目前尚属于初级阶段［7］。

国外众多学者对群桩桥墩局部冲刷做了大量的研究和实践工作。国际水力学协会组织国际专家编著出版一系列文件和手册，主要描述了影响桩群冲刷的机理，同时对双桩柱桥墩的局部冲刷特性进行了试验研究，提出了双圆柱体的桩群系数Kgγ，但未能给出计算公式；美国联邦公路局发布的行业规范，针对简单布设群桩的桥基在单向水流作用下的局部冲刷推荐了计算公式，用群桩相连的等效实体桩乘以群桩的间距校正系数来计算局部冲刷深度，即：式中：S为桩中心的间距；Φ为桩的直径；Ks为间距校正系数；Ka为迎流角校正系数；hb为等效实体桩的最大局部冲刷深度；a为墩宽；k2为水流冲击角系数；k3为河床状态系数；k4为床沙粒径系数；hp为一般冲刷后的水深；Fr为弗劳德数。

我国铁路和公路系统广泛协作，对非粘性河质桥墩局部冲刷进行了研究。对于群桩桥基的局部冲刷，我国行业规范采用“墩形系数法”进行预测计算，以一个单桩作为参照物，采用桩群系数计入桩群的影响来计算局部冲刷深度，这里桩群系数的物理意义相当于墩形系数。

我国铁路规范［8］中非粘性土河床的局部冲刷深度计算公式为：

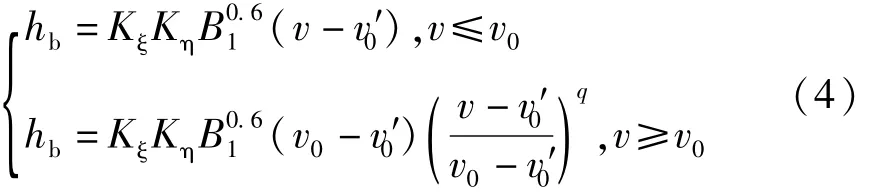
对于桩基承台桥墩，当承台地面高于水面时引进桩群系数 Km，代入公式（4）计算：

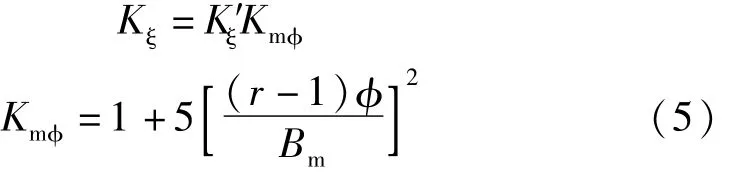
式中：hb为桥墩局部冲刷深度；Kη为河床颗粒影响系数；v为墩前水流行近流速；B1为桥墩计算宽度；v0为河床泥沙起动流速；v′0为墩前始冲流速；Kξ为墩形系数；K′ξ为单桩形状系数；Bm为桩群垂直水流的分布宽度；r为桩的排数；为桩径；q为指数。

当承台底面相对高度在0≤h／h≤1．0时，冲刷深度hb按下式计算：

式中：h为承台底到河床的距离；K为淹没桩体折减系数，；K、B按承台底处于ξ11一般冲刷线计算；Kh2为墩身承台减少系数。

为了获得整体的冲刷深度，还需要计算桥位处的一般冲刷深度，我国铁路规范［8］中对非粘性土河床的一般冲刷深度计算公式为：

式中：hp为桥下一般冲刷后的最大水深；hmc为桥下河槽部分的最大水深；hc为桥下河槽部分的平均水深；Bc为桥下河槽部分桥孔过水净宽；Qc为桥下河槽部分通过的设计流量；E为与汛期含沙量有关的系数；A为单宽流量集中系数；dc为河槽平均粒径，以mm为单位。

2 群桩基础等效刚度

当桥墩周围发生局部冲刷，基础埋深减小，引起桥墩墩身及上部结构的一系列变化，需要我们对其刚度进行重新验算。建立桥梁有限元模型时采用等效刚度模型，等效刚度模型就是承台处施加6个自由度的弹性约束，将桩基础的刚度简化到承台处，模拟桩基和土体对上部结构的影响。

根据文献［9］采用地基系数法，即m法，计算土的弹性抗力，将土视为具有随深度成正比增长的地基系数的弹性变形介质，深度y处垂直于基础侧面的水平地基系数Cy＝my，深度h处基底竖向地基系数C0＝m0h，m、m0为地基系数的比例系数。对于群桩基础，以构件相互影响系数k计入多构件对土的弹性抗力的影响。

定义桩群的刚度系数δAB为当承台发生单位B种变位时，所有桩顶（必要时包括承台侧面）引起的A种反力之和。忽略桩顶横向位移与转角的耦合关系，计算群桩基础的等效刚度可得到顺桥向平移刚度δaa1、横桥向平移刚度δaa2、竖向平移刚度δaa3和顺桥向抗扭刚度 δcc1、横桥向抗扭刚度 δcc2、竖向抗扭刚度 δcc3，如图1所示。

图1 群桩等效刚度示意图Fig．1 Schematic diagram of equivalent-stiffness model

计算得到的群桩基础等效刚度可以表述为以下矩阵形式：

3 基于全过程迭代的车桥系统动力分析

列车－桥梁动力耦合系统可分为列车子系统和桥梁子系统两部分，两者通过轮轨关系相联系，系统的激励源为轨道不平顺。

3.1 列车子系统

列车子系统模型由多节车辆组成。每节车辆模型都是由一个车体、两个转向架和四个轮对组成的多自由度体系，如图2所示。

将车体、转向架和轮对均视为刚体，忽略其在振动中的弹性变形。假定每个车体和转向架拥有横摆y、沉浮z、侧滚rx、点头ry和摇头rz共5个自由度，每个轮对有横摆、侧滚、沉浮共3个自由度，即每节车辆有27个自由度。忽略列车各节车辆之间的连接，不同车辆之间的振动不存在耦合关系，可以分别求解各节车辆的运动状态和轮轨力。

单节车辆的运动方程可以由下式表示：

式中：MV、CV、KV、XV分别是单节车辆的质量矩阵、阻尼矩阵、刚度矩阵以及单节车辆的位移向量；PV是作用在单节车辆上的外加力向量。车辆系统方程的建立方法参考文献［10－15］。

图2 车辆动力分析模型Fig．2 Dynamic model of vehicle system

3.2 桥梁子系统

桥梁子系统方程可以表示为

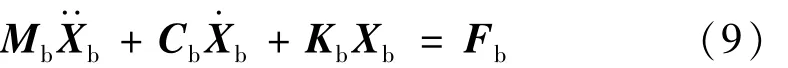
式中：Mb、Kb分别为桥梁子系统的质量矩阵和刚度矩阵，可由有限元法求得；Cb为桥梁子系统的阻尼矩阵，可由各类比例阻尼法求得；Xb为桥梁子系统的位移向量；Fb为作用在桥梁子系统的力向量，即轮轨间作用力，由下述的轮轨关系假定得到。

3．3 轮轨关系

轮轨间作用力作用于左右轮轨接触点。假定在竖向上轮对与钢轨密贴，轮轨间竖向作用力为常数，其值为一系悬挂力、轮对惯性力、静轴重三者之和。同时假定轮轨关系在横向上满足Kalker蠕滑理论，并且车轮与轨道间相对运动与其接触力之间符合线性关系。由文献［16］假定，横向蠕滑系数为常数，轮轨间横向作用力为蠕滑系数与轮轨横向运动速度的乘积，因此认为横向轮轨相互作用力与轮轨横向相对速度成正比。将式（8）右端项中车辆的速度项移至左端，即为

式中：CC为由于轮轨间蠕滑产生的附加阻尼矩阵。

3．4 全过程迭代法求解系统方程

将列车子系统方程和桥梁子系统方程联立，并设列车的节数为n，可得到车－桥耦合系统的动力方程为

式（11）中，前n行为列车子系统方程，后1行为桥梁子系统方程。本文采用全过程迭代法［17］求解系统方程，首先假定桥梁子系统为刚性，求解独立的列车子系统方程，得到列车动力响应及轮轨间作用力时程，然后将轮轨间作用力施加于桥梁，求解独立的桥梁系统方程而得到桥梁的动力响应，将求出的桥面动力响应时程与轨道不平顺叠加作为新的车辆系统激励进行下一步迭代。其计算过程见图3。

图3 全过程迭代计算过程Fig．3 Inter-system iteration process

由于在迭代过程中单独求解桥梁子系统方程，因此对于复杂或直接计算系统动力矩阵困难的桥梁，可利用通用有限元软件直接计算其在轮轨力时程作用下的动力响应，以代替建立和求解式（9）。

全过程迭代法每步计算即为全时程计算，而非针对单一时间步的计算。因此，每次列车或桥梁子系统的求解，分别得到列车或桥梁子系统全部计算时间内的响应过程，而非某一时刻的响应。

4 算 例

某跨江特大桥桥址区与河道呈垂直相交，桥墩基础采用桩基承台基础。桥梁2＃～5＃墩之间为（32＋48＋32）m的单线连续梁，5＃～9＃墩之间的梁为单线32 m简支梁，9＃～12＃墩之间为（40＋64＋40）m的单线连续梁，桥梁截面如图4～图6所示。桥墩之中4＃～10＃墩位于江上，受河流冲刷影响，墩高7～12．1 m。桥位所在位置河床宽约243 m，桥址处设计控制的水文数据为：设计流量 Q＝5 500 m3／s，设计水位 H＝240．95 m，河面宽度约256 m，平均水深约6．13 m，最大水深为7．02 m。据勘察揭露显示，桥址区地表层为粗砂、圆砾土等，下伏气孔状玄武岩，抗压强度为44．5 MPa。

图4 32＋48＋32 m连续梁截面图（单位：mm）Fig．4 Section of continuous beam with spans（32＋48＋32）m（Unit：mm）

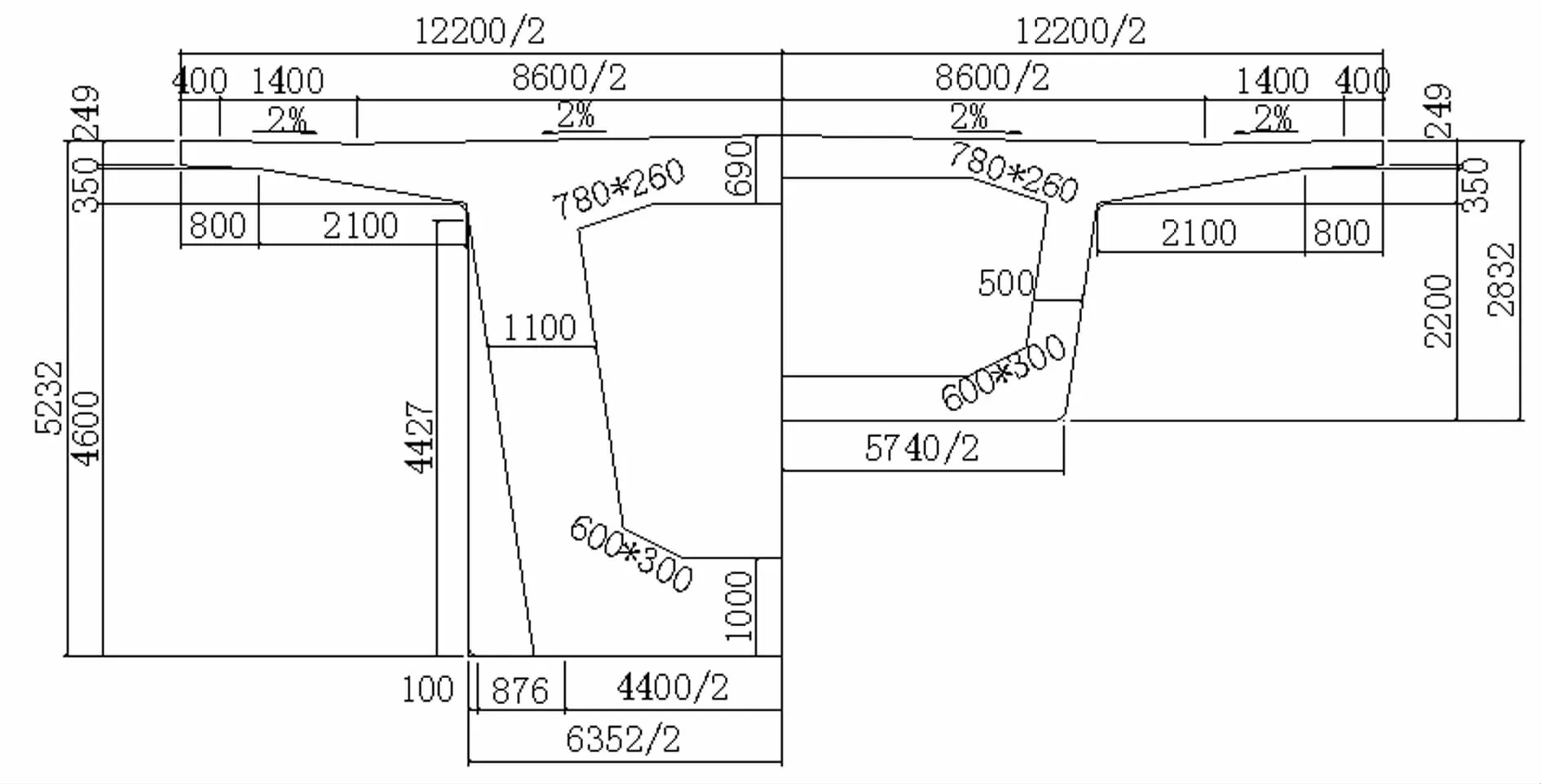
图5 40＋64＋40 m连续梁截面图（单位：mm）Fig．5 Section of continuous beam with spans（40＋64＋40）m（Unit：mm）

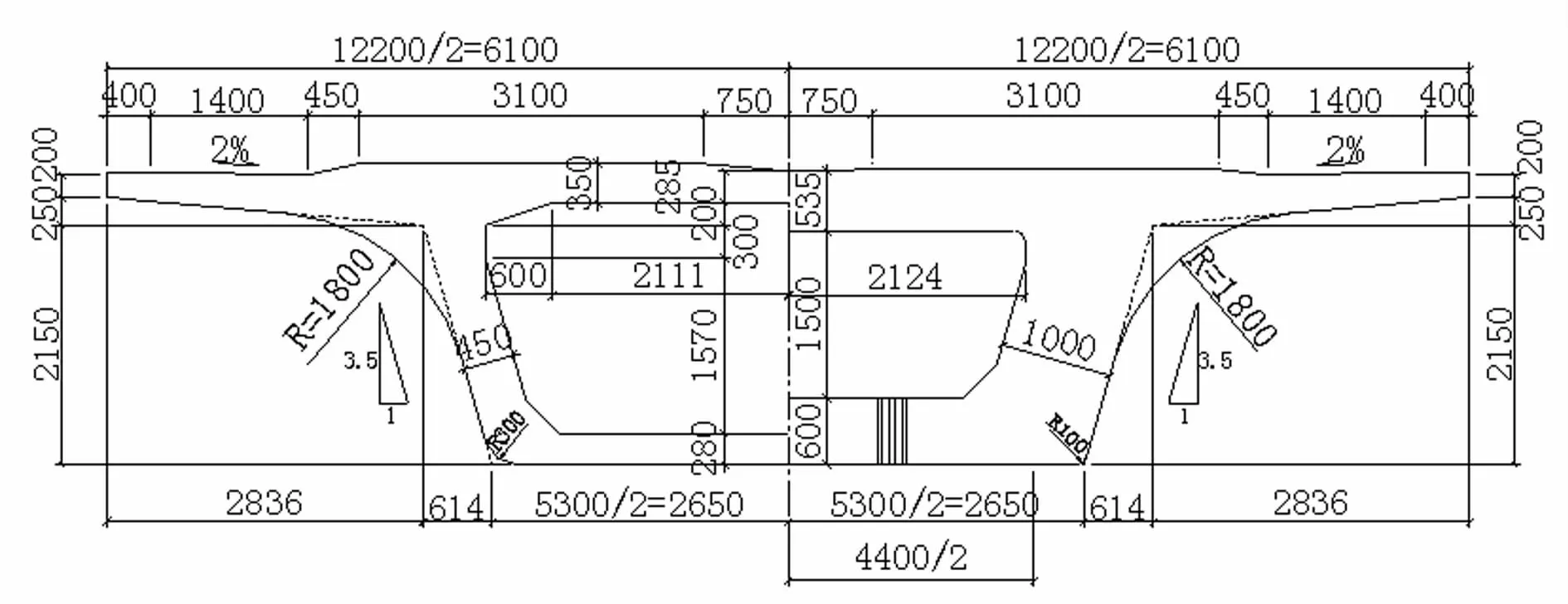
图6 32 m简支梁截面图（单位：mm）Fig．6 Section of 32 m span simply supported beam（Unit：mm）

本文采用有限元软件MIDAS建立该桥2＃～12＃墩之间桥跨的有限元模型，如图7所示。模型中以空间梁单元模拟墩梁，以主从节点模拟支座，以节点弹性支承模拟基础等对上部结构的影响，承台基底弹性约束的刚度按表4中取值，将桥梁二期恒载以提高材料密度的方法施加于梁体。

图7 桥梁有限元模型Fig．7 FE model of bridge

4．1 冲刷深度与等效刚度

结合实际的水文资料并根据式（7）计算得到一般冲刷深度，见表1。偏安全考虑，河道平均深度增大2．03 m。一般冲刷前后各墩承台埋深如表2中所示，负号表示桥墩在受到一般冲刷之后承台底面均高于一般冲刷线。

表1 一般冲刷计算参数及冲刷深度Tab．1 Calculation parameters and general scouring depth

表2 一般冲刷前后各墩承台埋深Tab．2 Buried depth of pile-caps pre and post general scouring

在计算局部冲刷深度时，4＃墩与10＃墩承台底面低于一般冲刷线，按上部实体进行计算，即按公式（4）计算；其它各墩按公式（6）计算。计算得到各墩局部冲刷深度见表3。局部冲刷之后，全部桥墩承台底面均高于冲刷线，并且桩身暴露相当长度。8＃墩冲刷前后如图8所示。

表3 各墩局部冲刷深度Tab．3 Local scouring depth of all piers

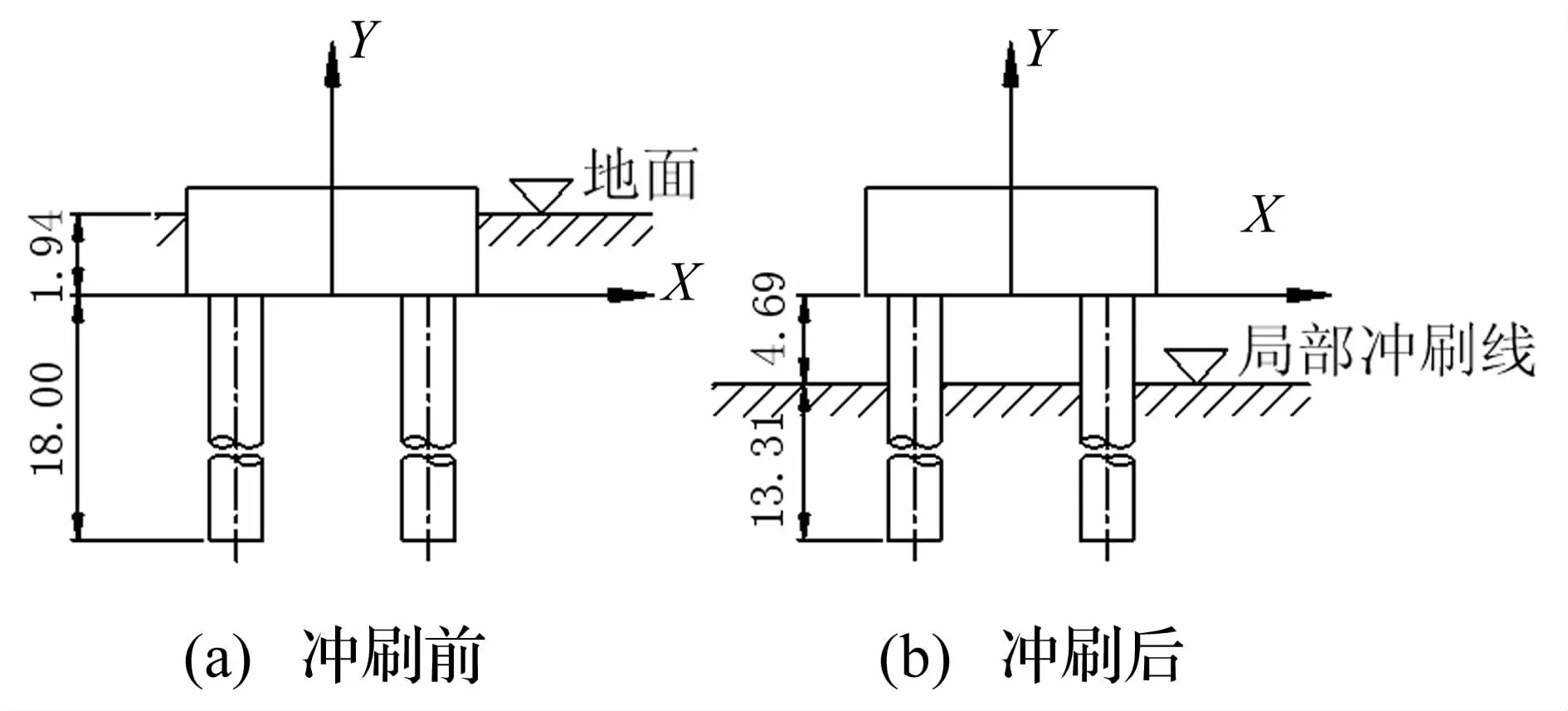
图8 8＃墩冲刷前后的基础埋深（单位：m）Fig．8 Variation of buried depth of 8＃pier（Unit：m）

图9 群桩分布图（单位：cm）Fig．9 Schematic diagram of pile-group（Unit：cm）

表4 冲刷前后各墩基础等效刚度（×109）Tab．4 Equivalent stiffness of foundation before and after scouring

该桥桩基础为钻孔桩，桩端置于一定深度的弱风化玄武岩中，各墩群桩分布如图9所示。各墩基础冲刷前后的等效刚度计算结果见表4。从表中结果可以看出，各墩基础等效刚度在冲刷之后都减小，其中水平方向的平移刚度与竖向的抗扭刚度减小最显著。冲刷之前，承台侧面受到土的抗力，冲刷之后，承台全部暴露在水中，只有土中的桩基础横向受力，刚度必然显著减小；该桥桩基础为端承桩，竖向刚度主要受基底竖向承载力影响，冲刷仅减小了承台底土的竖向抗力，对整体的竖向刚度的影响小于水平向刚度。

4．2 桥梁自振特性分析

通过有限元计算，得到该桥在冲刷前后的自振频率及响应振型，计算结果对比见表5。图10～图11所示为冲刷前后桥梁典型振型的振型图。在两联连续梁和多孔简支梁中有部分梁的振型是独立的。前10阶振型大部分出现在两端连续梁处，其中前3阶振型都出现在边跨（40＋64＋40）m连续梁处。冲刷之后，顺桥向与横桥向的一阶模态频率值均变小，一阶纵漂频率降低22．3%，一阶横弯频率降低8．4%。河流冲刷使得基础刚度减小，尤其是水平方向的刚度减小显著，桥梁整体变得更柔，顺桥向与横桥向的自振频率变低。

表5 自振频率及振型Tab．5 Free vibration characteristic

图10 冲刷前桥梁振型图Fig．10 Mode shapes of bridge before scouring

图11 冲刷后桥梁振型图Fig．11 Mode shapes of bridge after scouring

4．3 车桥响应分析

通过该桥的铁道线路为客货共线线路，由于货车单位延长重量远大于客车，其对桥梁基础及周围区域产生的振动亦大于客车，偏安全，计算中采用轴重较大的C70货车，计算无机车50节编组以90 km／h过桥时引起的振动状态。采用德国低干扰谱转换的时域不平顺样本作为轨道不平顺激励，截至波长80m。

由于货车车辆只有一系悬挂装置，在建立车辆子系统模型时，将公式（10）各矩阵中有关转向架自由度的行与列去掉即可。

计算中各工况时程积分的时间步长均为0．02 s。桥梁系统的阻尼按Rayleigh阻尼考虑，计入桥梁的一阶横向频率和一阶竖向频率。偏安全起见，各阶频率的阻尼比均取0．02。

如表6所示为冲刷前后车辆的最大振动响应结果，可以看出，冲刷前后列车行车时脱轨系数、轮轴横向力与车体加速度都小于容许值，横向与竖向平稳性达到优良的等级；桥墩基础受到冲刷之后，车辆的动力响应普遍增大，其中车体横向加速度变化最显著，最大值增大64%。轮重减载率在冲刷之间已经接近容许值，在冲刷之后值为0．64，超过了容许限值，影响行车安全。河流冲刷引起桩基础的刚度变化导致整个桥梁的振动模态发生变化，从而对车体的响应也造成影响，基础水平刚度的减小使得车体的横向响应变化显著。

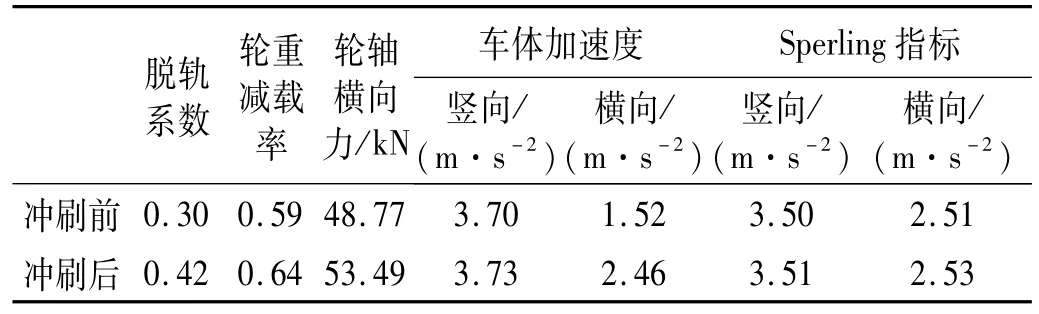
表6 冲刷前后车辆动力响应Tab．6 Dynamic responses of vehicle

表7给出了冲刷前后各梁的桥梁动力响应最大值。图12～图14给出了第2孔梁、第7孔梁与第9孔梁跨中的动力响应时程。

桥墩基础在受到冲刷之后桥梁各跨跨中竖向位移变化不大，竖向加速度略有减小，由于河流冲刷对于群桩基础竖向刚度影响较小，从而对桥梁竖向动力响应的影响不显著。

横向位移与横向加速度时程曲线呈现哑铃状，连续梁比简支梁更为明显。分析认为这是列车荷载突加突减引起的，列车长度大于桥梁长度，列车第一节车上桥与最后一节车出桥，使桥梁受到突加荷载与突减荷载，在跨中处冲击效应最大。冲刷之后，结构刚度变小，冲击效应减弱。连续梁跨度大于简支梁使得效应突增段比简支梁明显。

冲刷前后，横向位移与横向加速度有显著变化。中部第4孔～第7孔简支梁桥墩基础受到冲刷之后横向位移与横向加速度都明显增大，其中第7孔梁横向动力响应增加最为显著，横向位移增大1．44倍，横向加速度增加84%。河流冲刷使得桥梁水平方向刚度减小，横向车致振动响应增大。

两联连续梁桥的横向响应时程曲线形状差异较大。第1、第2、第9、第10孔梁在桥墩基础冲刷之后横向位移与横向加速度都减小，其中第2孔梁横向位移幅值减小54%，横向加速度幅值减小67%。桥梁横向响应振型在冲刷之前基本是独立的，而冲刷之后与简支梁耦合在一起。在1～3孔连续梁体系中，冲刷后第3孔梁与简支梁刚度减小，而第1、2孔梁刚度下降不显著，故此连续梁振型形状有较大改变。冲刷前后桥梁横向振动能量基本保持不变，由于第3孔梁振动加剧，因而第1、2孔梁振幅反而有所下降。8～10孔梁在冲刷之后横向自振频率降低，横向响应的变化除与1～3孔梁相同的原因外，还有车桥体系共振的因素。车体横向一阶自振频率为1．809Hz。冲刷之前，桥梁第3阶频率为1．772Hz，与车体的横向自振频率接近，当列车经过桥梁时发生横向共振作用。梁的第3阶频率振型独立，为8～10孔梁横弯振型，对中间简支梁影响不大。而在冲刷之后，梁的各阶横向频率及其谐波频率均远离车体横向自振频率，未发生共振。第9、第10孔梁桥墩未直接受到河流冲刷，河流冲刷作用的影响较小，受共振作用影响大。故冲刷之后，第9、10孔梁的横向响应减小。

表7 桥梁动力响应最大值Tab．7 Maximum dynamic responses of bridge

图12 2号梁跨中动力响应时程Fig．12 Dynamic responses of 2＃span

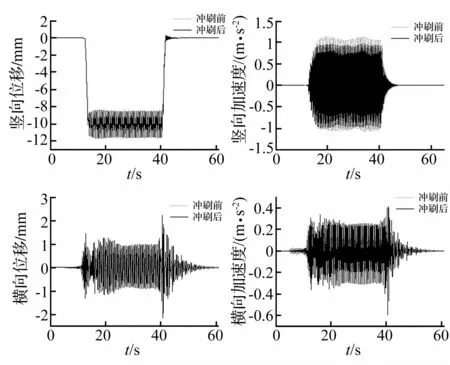
图13 7号梁跨中动力响应时程Fig．13 Dynamic responses of 7＃span

图14 9号梁跨中动力响应时程Fig．14 Dynamic responses of 9＃span

5 结 论

本文计算了群桩基础的冲刷深度，采用地基系数法计算群桩承台基础的等效刚度。在桥墩墩底以多自由度弹簧约束模拟基础等效刚度，建立了考虑河流冲刷作用的车桥耦合动力分析模型，采用全过程迭代方法求解系统方程。得出以下结论：

（1）在冲刷之后，全部桥墩承台底面均高于冲刷线，桥墩基础由低承台基础变成高承台基础，各墩基础等效刚度在冲刷之后都减小，其中水平方向的平移刚度与竖向的抗扭刚度减小最显著。

（2）桥墩基础受到冲刷之后，车辆动力响应普遍增大，其中车体横向加速度变化最显著，最大值增大62%。

（3）边跨连续梁未受冲刷梁跨，在整个桥梁受到河流冲刷之后横向响应减小，其中第2孔梁横向位移减小54%，横向加速度减小67%；简支梁受冲刷之后跨中横向位移与横向加速度明显增大，其中7＃梁横向动力响应增加最为显著，横向位移增大1．44倍，横向加速度增加84%。

（4）铁路桥梁跨越江海时广泛采用群桩承台基础，易受到水流冲刷的影响，应对桥梁结构的桩基、承台进行合理设计，并使用考虑水流冲刷作用的模型进行动力仿真以保证行车的平稳性和安全性。

［1］李梦龙．潮流作用下桥墩局部冲刷研究［D］．天津：天津大学，2012．

［2］沈周．铁路桥梁扩展基础冲刷探测与稳定性分析［D］．长沙：中南大学，2006．

［3］吴定俊，周建民，余华．高速铁路桥梁梁墩基础体系列车过桥动力分析［J］．上海铁道大学学报，2000，21（10）：44－49．WU Ding-jun，ZHOU Jian-min，YU Hua．Dynamic analysis of vehicle-bridge system including pier and foundation［J］．Journal of Shanghai Tiedao University，2000，21（10）：44－49．

［4］蒋通，马超勇，张昕．弹性支撑条件下车－桥体系的振动分析［J］．力学季刊，2004，25（2）：256－263．JIANG Tong， MA Chao-yong， ZHANG Xin． Dynamic analysis of train-bridge system with elastic supports［J］．Chinese Quarterly of Mechanics，2004，25（2）：256－263．

［5］单德山，李乔．考虑桩土作用的铁路曲线梁桥车桥耦合振动分析［J］．重庆交通学院学报，2004，23（6）：10－14．SHAN De-shan，LI Qiao．Coupled vibration analysis of railway simple-supported curved-girder bridges and vehicles with soil-structure interaction［J］．Journal of Chongqing Jiaotong University，2004，23（6）：10－14．

［6］李小珍，刘德军，晋智斌．大跨度铁路悬索桥车－线－桥耦合振动分析［J］．钢结构，2010，25（140）：6－12．LI Xiao-zhen，LIU De-jun，JIN Zhi-bin．Analysis of traintrack-bridge coupled vibration of a railway long-span suspension bridge［J］．Steel Construction，2010，25（140）：6－12．

［7］周泳涛，高正荣，鲍卫刚．复杂群桩基础冲刷计算方法研究［J］．公路，2012，（4）：26－29．ZHOU Yong-tao，GAO Zheng-rong，BAO Wei-gang．A study on erosion calculation method of complex pile group foundation［J］．Highway，2012，（4）：26－29．

［8］中华人民共和国铁道部．TB 10017－99铁路工程水文勘测设计规范［S］．北京：中国铁道出版社，1999．

［9］中华人民共和国铁道部．TB 10002．5－2005铁路桥涵地基和基础设计规范［S］．北京：中国铁道出版社，2005．

［10］张楠，夏禾，程潜，等．制动力作用下车辆－车站结构耦合动力分析［J］．振动与冲击，2011，30（2）：138－143．ZHANG Nan，XIA He，CHENG Qian， et al． Analysis method for a vehicle coupled system under braking force［J］．Journal of Vibration and Shock，2011，30（2）：138－143．

［11］ Zhang N．Xia H．et al．A vehicle-bridge linear interacted model and its validation ［J］． International Journal of Structural Stability and Dynamics，2010，10（2）：335－361．

［12］夏禾，张楠．车辆与结构动力相互作用［M］．2版．北京：科学出版社，2005．

［13］ Xia H，Zhang N，Guo W．W．Application of train-bridge interaction analysis to bridge design of high-speed railways in China［C］．Proceedings of ISEV2009．Beijing：Science Press，2009：965－975．

［14］Zhai W M，Xia H，Cai C B．High-speed train-track-bridge dynamic interactions-Part I：theoretical model and numerical simulation［J］．International Journal of Rail Transportation，2013，1（2）：3－24．

［15］ Zhai W M，Wang S L，Zhang N．High-speed train-trackbridge dynamic interactions-Part II：experimental validation and engineering application［J］．International Journal of Rail Transportation，2013，1（2）：25－41．

［16］翟婉明．车辆－轨道耦合动力学［M］．3版．北京：科学出版社，2007．

［17］张楠，夏禾．基于全过程迭代的车桥耦合动力系统分析方法［J］．中国铁道科学，2013，34（5）：32－38．ZHANG Nan，XIA He．A vehicle-bridge interaction dynamic system analysis method based on inter-system iteration［J］．China Railway Science，2013，34（5）：32－38．