基于损伤的HTPB推进剂/衬层界面内聚法则构建①

钮然铭，陈 雄，周长省，周清春

(南京理工大学机械工程学院，南京 210094)

基于损伤的HTPB推进剂/衬层界面内聚法则构建①

钮然铭，陈 雄，周长省，周清春

(南京理工大学机械工程学院，南京 210094)

为提高丁羟(HTPB)推进剂/衬层界面数值仿真结果的准确性，首先改进了单搭接试件，通过剪切实验获取界面断裂参数，而后分别采用双线型模型和指数型模型对试件进行数值研究，进行影响分析，并在此基础上建立了一种基于损伤变量的自定义内聚力模型，使模型具有了明确的物理含义。结果表明，改进的单搭接试件能够测定柔韧粘接件的II型断裂参数;II型界面断裂时，内聚力曲线形式与实验曲线形式一致;该基于损伤的内聚力模型能够比双线性模型和指数型模型更准确地反映HTPB推进剂/衬层界面的II型断裂性质。

内聚力模型;推进剂/衬层;数值研究;脱粘

0 引言

在航天和军工领域中，贴壁浇注装药结构由于推进剂能量高、装填系数高的特点，在火箭发动机中应用越发广泛。而推进剂和衬层的粘结界面是其结构完整性的薄弱环节，据美国国家宇航局统计，一个世纪以来，近三分之一的发动机事故都是由于界面脱粘引起的［1］。在发动机制造时，复合推进剂一般在高温下直接浇注于衬层内部固化，由于推进剂和衬层材料的热力学性质不匹配，冷却固化时会两者会产生相互作用。此外，储存时的气温变化也会产生同样的影响。通常由于轴向尺寸较长，其相对变形比径向更加明显。所以，剪切(II型)作用更加显著。此外，在发动机发射和飞行时，由于惯性作用，推进剂/衬层界面更是以II型相互作用为主。因此，研究该界面的II型断裂，对于发动机结构完整性研究具有重要意义。

针对推进剂/衬层界面的研究方法主要分为两类:一类是实验研究方法，如通过实验获取界面裂纹的扩展规律，对界面进行无损检测，以及超声、红外、微波、散斑等方法［2－4］;另一类是数值研究方法，如建立三区域界面层模型来预测界面强度［5］，对固体火箭发动机界面脱粘进行仿真分析［6］。

近年来，针对粘接界面的数值研究得到了越来越多的重视。尤其是在 Barenblatt［7］提出内聚力模型(CZM)方法后，界面层的数值仿真研究受到越来越多的关注。随着理论的发展和学者们经验的积累，逐渐衍生出了多种内聚力模型形式。其中，常用的有双线型内聚力模型［8］和指数型内聚力模型［9］等。在Chandra［10］的文献中有更多模型的综述。也有学者采用内聚力模型方法，对丁羟(HTPB)推进剂/衬层界面进行研究，但却十分有限。Han［11－12］建立了 HTPB 推进剂的内聚力断裂模型，并采用内聚单元杂交的方法，模拟了推进剂粘弹性断裂过程。Zhou［13］采用将实验和反演相结合的方法，获取了HTPB推进剂/衬层间的张开型(I型)断裂参数。Niu［14］采用类似的方法，对HTPB推进剂/衬层的剪切型(II型)断裂进行研究。这些研究都是HTPB推进剂/衬层II型断裂研究的基础。

本文将首先针对HTPB推进剂/衬层界面进行实验研究，采用改进的单搭接层叠试件进行实验，获得断裂性质以及实验应力-应变曲线。而后，分别采用双线型和指数型内聚力模型，对试件粘接层进行数值仿真;然后，通过比较仿真结果，研究内聚力模型的形式对仿真结果的影响。最终，提出一种基于实验取得的损伤变量演化规律的自定义内聚力模型的构建方法。相对于双线性模型和指数型模型，该模型可得到更准确的HTPB推进剂/衬层界面II型断裂仿真结果。本研究为HTPB固体推进剂火箭发动机的装药结构完整性分析提供界面层模型。

1 实验

由于衬层具有极好延展性，如果直接加载会产生较大的变形，推进剂是固体颗粒填充材料，如直接施加拉伸力，会对其产生明显的损伤，对实验的准确性造成影响。由于标准单搭接［15］试件不能够满足该测试条件，本次试验采用了改进的推进剂/衬层层叠试件，通过将层叠件粘接在阶梯型铝合金夹具上，而避免试验机的直接加载。通过对该试件进行三维仿真［14］，发现该试件中界面层的力学分布以剪切力为主，只有在粘接层端部会存在较小的剥离力。因此，通过这样的设计，可获得以II型断裂为主的加载环境。

试件的制备过程如下:

(1)制备铝合金夹具，打磨粘结表面以便于粘结。将所需的推进剂和绝热层切削至40 mm×25 mm×5 mm的长方体;

(2)调配丁羟胶:将HTPB和IPDI(异佛尔酮二异氰酸酯)于容器中进行混合，置于40℃的电子水浴锅中水浴30 min，同时采用电子行星搅拌机进行不停歇地均匀搅拌;

(3)将混合物置于70℃的真空保温箱中，保温120 min后，丁羟胶即制备完成;

(4)采用丁羟胶粘结推进剂和衬层，施加适当的压力排除界面系统中的空气，清除多余的丁羟胶，以免固化时流出，污蚀被粘接件的其他表面;

(5)将试件置于70℃的真空保温箱中保温7 d，再置于室温下，真空保存8 d;

(6)采用环氧树脂基速干强力胶，将层叠件粘接到铝夹具打磨后的表面上，待其完全固化之后，即可进行实验。

试件结构及其夹持方式如图1所示。

图1 丁羟推进剂/衬层界面层叠单搭接试件Fig.1 HTPB propellant/insulation cohesive adherend sandwich SLJ

实验于常温25℃、相对湿度45%条件下进行。通过电子万能试验机(倾技®QJ-211;中国上海)，对该试件进行了9组拉伸实验。最终得到的工程应力-工程应变曲线如图2所示，曲线的峰值点即界面的断裂强度为。力-位移曲线下的面积可通过积分得到，再对试件初始粘结面积平均，得到界面的断裂能。得到的界面参数如表1所示。

图2 实验测定的工程应力-工程应变曲线Fig.2 Experimental nominal stress to nominal strain curve

表1 界面参数Table 1 Interface parameters

2 数值研究

内聚力模型是建立胶粘层所常用一种方法，最初是由 Barenblatt［7］提出的，在内聚力模型方法中，将界面粘结层视为一排并列的弹簧［16］，通过牵引-分离法则定义每个弹簧的力学响应，得到每个单元损伤起始和演化的形式，通过多个单元并列，进而模拟出整个界面的裂纹起始和扩展过程。

2.1 双线型内聚力模型

双线型内聚力模型［8］如图3所示。

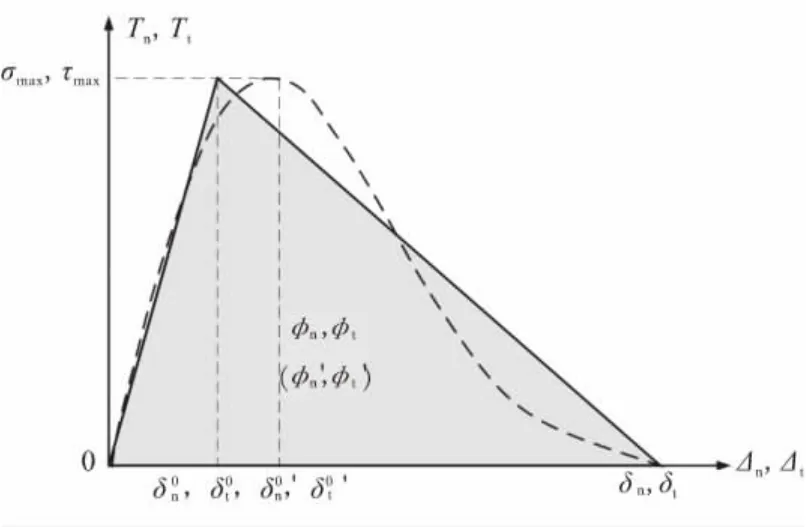
图3 典型的法向和切向双线型和指数型内聚力模型Fig.3 Typical billinear and exponential CZM in normal and tangential direction

牵引分离法则如下，

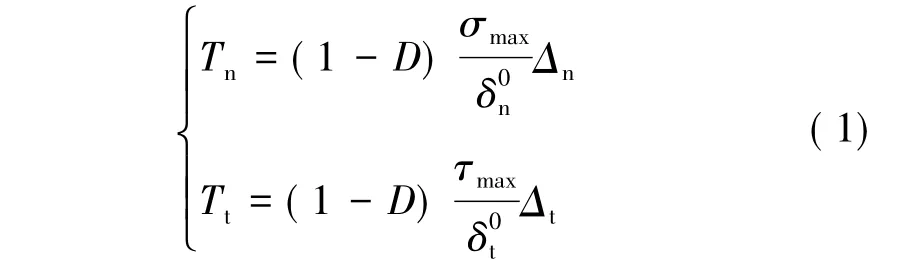
式中 角标n、t分别为法向、切向参数;Δ为自变量分离位移;T为牵引力;σmax和τmax分别为法向和切向的断裂强度;δ0为临界位移，表示牵引力达到断裂强度时对应的分离位移;D为损伤变量。

损伤变量D定义如下:

式中 δ为特征位移，表示最大分离位移。

2.2 指数型内聚力模型

指数型内聚力模型［9］如图3所示，牵引分离法则如下:

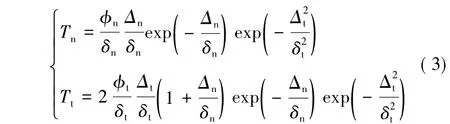
其中，φ为断裂能，断裂能和断裂强度之间的关系如下:

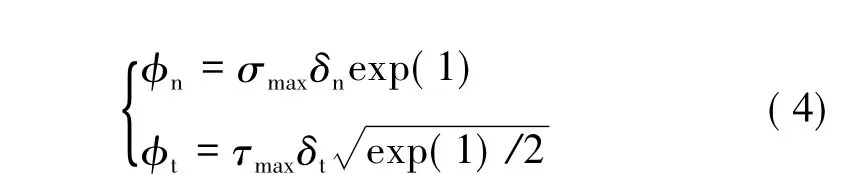
该模型需要采用UMAT(User-defined Material)子程序的形式导入到仿真软件中。采用Fortran语言分别编译式(3)、式(4)，并将式(3)做偏分，转化为雅各比矩阵即可。

2.3 网格和结果

图4以SDEG云图的形式给出了数值研究的网格模型和仿真结果，SDEG是表征界面单元损伤程度的无量纲量，0表示完全无损，1表示完全失效。该图给出了界面完好无损和彻底失效2个极限状态。模型中，界面层的厚度在视觉上进行了放大，以便于观测，定义其计算厚度初始值为0.2 mm。另外，为了使数值分析具备更好的收敛性，模型采用网格偏移的网格划分方法，对靠近界面和端部的网格加密。接下来，采用不同形式的内聚力模型进行仿真。

图4 有限元网格及仿真结果Fig.4 Finite element mesh and simulation result

3 CZM影响分析及自定义内聚力模型

3.1 影响分析

牵引-分离法则为内聚力模型的本质，它表达了单个单元的应力-应变关系。通过理论计算，可清楚地比对出同样界面参数情况下双线型模型和指数型模型之间的区别和联系。图5中给出了定量化的指数型内聚力模型曲线。

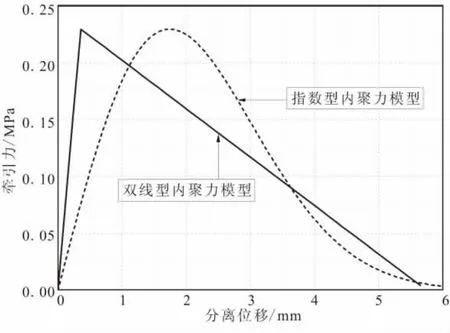
图5 双线性内聚力模型和指数型内聚力模型Fig.5 Billinear CZM law ＆ exponential CZM law

从图5可看出，在同样界面参数的情况下2种模型的峰值相同;双线型内聚力模型的特点在于其形式比较简单，并且计算上方便快捷，仿真出的曲线强化段为线性增长，与实验曲线的上升段对应得较好;而指数型模型的优点则是其能够较为真实地反映材料的软化特性，能够较好的和试验曲线的下降段相对应。

接下来，分别采用2种模型进行仿真，分别得到应用指数型、双线型内聚力模型的仿真结果，以及它们和试验曲线的比较结果。如图6所示，双线型模型强化段为线性，与实验曲线符合较好，指数型内聚力模型的上升段则软化得过多，与曲线存在较明显的差异，但在损伤开始后，其曲线形式和实验曲线的趋势非常相近，不过拖尾段又不符合材料的特性。双线型内聚力模型和指数型模型各有优点，但它们和实验结果仍普遍存在着较大的差异。

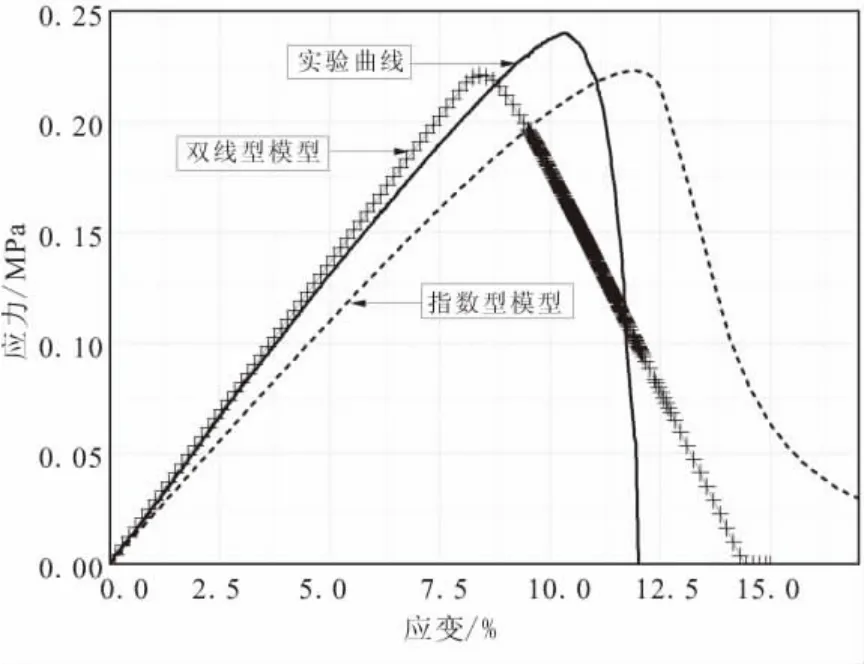
图6 双线型和指数型内聚力模型仿真结果与实验曲线对比Fig.6 Comparision among the simulation results of bilinear CZM law＆exponential CZM law and experimental result

通过对仿真结果进行比较和观察，可看出仿真得到的曲线形式和预先定义的内聚力模型相近似，表征着界面的宏观性质和微观性质之间存在着一定的联系［10］，而决定内聚力模型形式的是损伤的演化。所以，如果能够获取在实验中材料的真实损伤演化方式，就可获取一个曲线形式和实验一致的内聚力模型，如采用该模型，仿真结果的准确性会得到提高。

3.2 自定义内聚力模型

根据实验曲线上升段线性，下降段加速损伤的特点，定义一种损伤演化形式如下:

将这个损伤演化形式带入到式(1)中，对实验测定的胶粘层的单位面积力-位移曲线进行拟合，拟合结果见图7。拟合曲线的强化阶段继承了双线型模型的线性特点，使得在后续的刚度调整变得简便易行。损伤演化阶段继承了指数型模型的特点，能够较真实地反映材料的软化性质。

接下来，调整模型的初始刚度，使得模型的刚度和材料相匹配。保持模型的断裂强度，断裂能和特征位移不变，将损伤演化的形式在新区间内进行缩放，即式(5)中的 δ0由4.2 mm 调整为0.8 mm，最终得到了自定义内聚力模型，如图7所示。

图7 自定义内聚力模型的建立Fig.7 Construction of the customized CZM

3种模型的损伤变量演化形式均可通过式(1)反求出来，如图8所示，D为随着Δ－δ0变化的函数。

图8 3种模型的损伤演化Fig.8 Damage evolution of the three CZMs

自定义内聚力模型的损伤演化趋势位于双线性内聚力模型和指数型内聚力模型之间。由于自定义模型的损伤演化方式是通过实验结果反求而来，因此比较真实地反映了粘接剂真实的损伤演化形式，使得该自定义模型具有了一定的物理基础，通过建立具备材料损伤演化本质的内聚力模型，使数值计算有理可循，结果更加准确。

损伤演化可采用列表的形式输入到商业有限元软件Abaqus®中。采用该自定义的内聚力模型，最终得到仿真结果如图9所示。

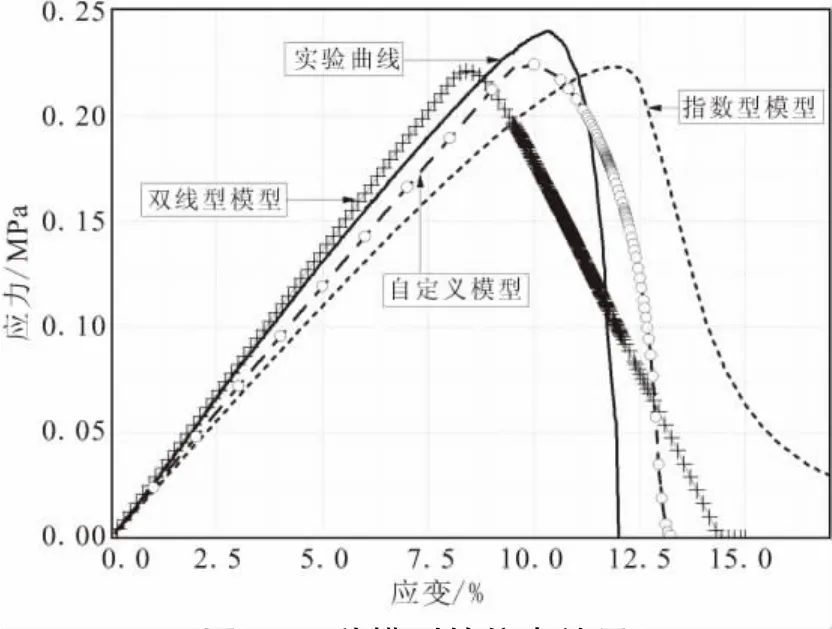
图9 3种模型的仿真结果Fig.9 Simulation results of the three CZMs

通过比较可发现，相比于双线型模型和指数型模型，采用自定义内聚力模型仿真HTPB推进剂/衬层界面能够得到更准确的结果，具有显著的优势。曲线的损伤起始阶段和损伤演化阶段都具有和实验结果相近似的趋势。另外，值得说明的是，3条曲线在强度和能量上的偏差是由实验中所不可避免的界面法向剥离力和粘结区域端部的应力集中现象所导致的。构建该模型的方法具有广泛的适用性，可适用于其他柔韧性被粘接件的II型界面断裂的性质预测。由于该自定义模型是基于界面真实的损伤演化方式而建立的，具有明确的物理意义。因此，通过该内聚力模型的数值仿真具有更高的可信度和准确性。

4 结论

(1)改进单搭接实验，用于测定柔韧材料界面的II型断裂参数，能够有效消除剥离力，获取以II型为主的加载环境。HTPB推进剂/衬层界面在1 mm/min的加载速率下，II型断裂强度为 0.237 6 MPa，II型断裂能为 0.660 3 N·mm。

(2)针对改进单搭接试件进行数值分析，通过比较双线性内聚力模型和指数型内聚力模型的仿真结果，验证了界面II型断裂时，内聚力曲线形式与仿真曲线形式一致的结论。

(3)通过拟合实验曲线反求损伤变量D，可构建自定义内聚力模型，因为融入了界面层粘接剂的真实损伤演化形式，所以该模型具备了明确的物理含义，可提高HTPB推进剂/衬层界面的仿真精度，该建模方法可适用于其他柔韧性被粘接件的II型界面断裂的性质预测。

［1］David S.Disasters and accidents in manned spaceflight［M］.Springer，2000.

［2］Srinivas M V，Ravichandran G.Interfacial crack propagation in a thin viscoelastic film bonded to an elastic substrate［J］.Int.J.Fract.，1994，65(1):31-47.

［3］Fraisse P，Schmit F.Use of J-integral as fracture parameter in simplified analysis of bonded joints［J］.Int.J.Fract.，1993，63(1):59-73.

［4］Wu S R，Lu Y C，Kuo K K，et al.Anomalous combustion of solid propellant in a propagating debond cavity［J］.AIAA，1992，92:6-9.

［5］邸克，杨月诚.固体推进剂/衬层界面脱粘裂纹的三区域界面层模型［J］.推进技术，2012，33(4):603-608.

［6］刘甫.粘弹性界面断裂与固体火箭发动机界面脱粘研究［D］.长沙:国防科技大学，2005.

［7］Barenblatt G I.The mathematical theory of equilibrium cracks in brittle fracture［J］.Adv.Appl.Mech.，1962，55(7):104.

［8］Camanho P P，Davila C G.Mixed-mode decohesion finite elements for the simulation of delamination in composite materials［J］.NASA-Technical Paper，2002，211737(1):33.

［9］Van Den Boshi M J，Schreurs P J G，Geers M G D.An improved description of the exponential Xu and Needleman cohesive zone law for mixed-mode decohesion［J］.Eng.Frac.Mech.，2006，73(9):1220-1234.

［10］Chandran N，Li H，Shet C，et al.Some issues in the application of cohesive zone models for metal-ceramic interfaces［J］.Int.J.Solids Struct.，2002，39(10):2827-2855.

［11］韩波，鞠玉涛，周长省.HTPB推进剂粘聚断裂研究［J］.固体火箭技术，2013，36(1):94-97.

［12］Han Bo，Ju Yu-tao，Zhou Chang-sheng.Simulation of crack propagation in HTPB propellant using cohesive zone model［J］.Eng.Fail.Anal，2012，26:304-317.

［13］Zhou Qing-chun，Ju Yu-tao，Wei Zhen，et al.Cohesive zone modeling of propellant and insulation interface debonding［J］.J.Adhesion，2014，90:1-22.

［14］Niu Ran-ming，Zhou Qing-chun，Chen Xiong，et al.Experimental and numerical analysis of mode II fracture between propellant and insulation［J］.International Journal of Adhesive and Adhesion(just accepted).

［15］BS-ISO-11003-2-2001.Adhesives-determination of shear behaviour of structural adhesives-part 2:Tension test using thick adherends［S］.2001.

［16］Yuval F，Leslie B S.A new cohesive zone model for mixed mode interface fracture in bimaterials［J］.Eng.Frac.Mech.，2008，75(15):4583-4593.

(编辑:刘红利)

Construction of HTPB propellant/insulation CZM base on damage

NIU Ran-ming，CHEN Xiong，ZHOU Chang-sheng，ZHOU Qing-chun
(Department of Mechanical Engineering，Nanjing University of Science and Technology，Nanjing 210094，China)

In order to raise the precision of the numerical simulation result of HTPB propellant/insulation，firstly，the SLJ test was improved and conducted to obtain the interface parameters.Then the bilinear CZM and the exponential CZM were adopted to conduct the numerical analysis，separately.At last，an influence analysis was made and a customized CZM model was built base on damage variable，which gave the model a significant physical meaning.The result shows that the improved SLJ test can determine the interface parameters of ductile adherends.The CZM law has a similar trend to the simulation curve，and the CZM based on damage can better simulate mode-II interface fracture properties between HTPB propellant and insulation than bilinear CZM and exponential CZM.

cohesive zone model;propellant/insulation;numerical research;debond

V512

A

1006-2793(2014)06-0819-05

10.7673/j.issn.1006-2793.2014.06.015

2013-11-14;

2014-01-21。

装备预先研究基金(20101019)。

钮然铭(1990—)，男，硕士生，研究方向为推进剂/衬层界面断裂力学及固体力学。E-mail:niuranming@outlook.com