宽粒径范围颗粒对气相膨胀的影响①

刘加宁，郜 冶，刘平安，张喜峰

(1.哈尔滨工程大学航天工程系，哈尔滨 150001;2.北方华安工业集团有限公司，齐齐哈尔 161046)

宽粒径范围颗粒对气相膨胀的影响①

刘加宁1，郜 冶1，刘平安1，张喜峰2

(1.哈尔滨工程大学航天工程系，哈尔滨 150001;2.北方华安工业集团有限公司，齐齐哈尔 161046)

利用双流体模型对固体火箭发动机喷管内气固两相流进行计算，研究了两相流中颗粒相与气相的相互作用，分析了颗粒粒径及颗粒质量分数对两相流中气相在喷管中膨胀的影响。结果表明，颗粒粒径造成两相流损失的大小是颗粒比表面积、气相湍流动能及颗粒在喷管内的滞留时间等因素共同作用的结果，两相流损失随着颗粒粒径的增大先增大、后减小，同时随着颗粒质量分数增大而增大;JPL喷管中粒径为2 μm的颗粒造成的两相流损失最大，此粒径下，当颗粒质量分数从10%增大到40%时，两相流损失从10%增大到26%。

喷管;两相流;双流体模型;颗粒;气相

0 引言

为提高推进剂的能量和抑制不稳定燃烧，通常向固体火箭发动机推进剂中添加铝粉。铝粉燃烧后，产生的Al2O3质量分数能达到30%左右，随之带来的两相流动对发动机的性能造成很大影响，喷管膨胀过程的两相流损失可占到整个喷管损失的1/3～1/2。因此，研究固体火箭发动机喷管两相流动极为重要。

国内外对固体火箭发动机两相流进行了大量研究。Cuffel［1］对小喉部壁面曲率半径/喉部半径的 Jet Propulsion Laboratory(JPL)喷管进行冷流实验，得出在喉部中心线附近马赫数为0.8，喉部壁面处马赫数为1.4，给出3种预测小喉部壁面曲率半径/喉部半径跨音速流动的方法。张宏安［2］介绍了引起固体火箭发动机两相流动损失的凝聚相微粒的尺寸分布及测试方法的研究现状。Hwang等［3－5］利用颗粒轨道模型对固体火箭发动机喷管进行了计算，给出了颗粒的轨迹以及颗粒相速度和温度的分布，得出颗粒越大，速度滞后和温度滞后越大，同时喷管扩张段无颗粒区也越大。Chang等［6－8］采用双流体模型喷管两相流进行计算，研究了不同颗粒粒径及不同颗粒质量分数的喷管内流场，发现颗粒的粒径越小、质量分数越大，对气相的影响越大。刘静、严红等［9－10］对两相流中颗粒相对气相的影响进行了研究，得出粒径越大、颗粒质量分数越大，对气相的影响越大。

国内外大多数的两相流研究中，存在的问题是在讨论颗粒粒径对气相的影响时，仅选取了较少种颗粒粒径进行研究。目前，得出的结论主要有两种:一是随着颗粒粒径的增大，两相流损失增大;二是随着颗粒粒径的增大，两相流损失减小。这两种完全相反结论的产生可能是由于计算时仅选取了较少种颗粒粒径，这可能会使计算结果具有偶然性，计算结果不全面。为了确定颗粒粒径对两相流损失的影响，需要选取多种颗粒粒径进行研究。因此，本文利用双流体模型，对大范围变化的多种不同粒径的颗粒及4种不同颗粒质量分数的情况进行计算，研究颗粒粒径以及颗粒质量分数对两相流损失的影响。

1 计算方法及计算条件

本文基于计算流体力学软件ANSYS FLUENT 14.0，利用多相流模型中的Eulerian模型，气相作为第一相，为可压缩相，颗粒相作为第二相。压力-速度的耦合采用Phase Coupled SIMPLE格式，密度、动量、能量、体积分数、湍流动能和湍流耗散率方程的离散均采用First Order Upwind，湍流模型采用k-ε Dispersed Turbulence Models湍流模型。

边界条件:入口采用质量流量入口，气相给定气相质量流率mg、气相总温T0和气流方向，给定气相湍流动能k和湍流耗散率ε，颗粒相给定颗粒质量流率mp、颗粒粒径Dp、入口速度Vp和温度Tp;出口采用压力出口，由于出口是超音速出口，因此出口各参数通过内部参数外推得到;固体壁面条件采用绝热无滑移条件。

2 数值计算结果与分析

2.1 计算方法可靠性验证

为验证本文计算方法，首先对文献［1］中的JPL喷管单相流进行计算，并将计算结果与实验数据进行对比。模拟工况为燃气总压p0=4.763 atm，总温T0=300 K，计算网格如图1所示。

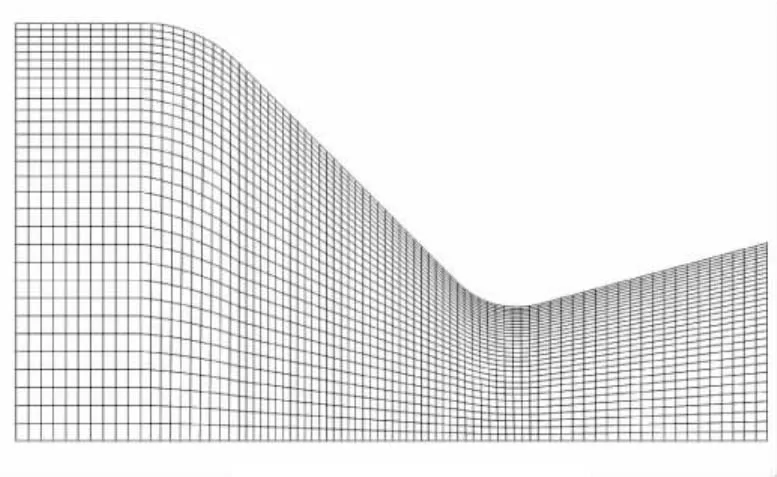
图1 计算网格Fig.1 Calculation nozzle grid

图2和图3分别为本文计算出的轴线压力和轴向马赫数与实验值的比较。可看出，计算值与实验值吻合得很好。

利用此方法选取 Dp分别为 2、10、20、50 μm 的 4种颗粒，颗粒质量分数mp/m=30%，其中m=mg+mp，以单相流的结果作为两相流计算的初始条件，对文献［6］中的JPL喷管进行计算。

图4为单相流和不同Dp的两相流气相的马赫数沿轴向的分布。

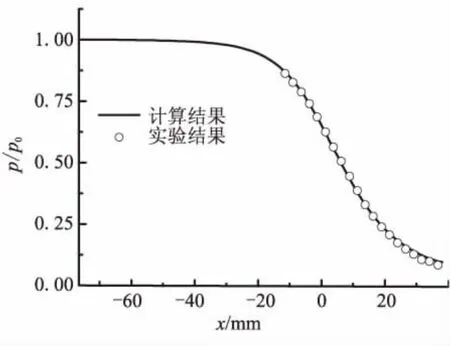
图2 轴线压力分布计算值与实验值Fig.2 Pressure along nozzle centerline

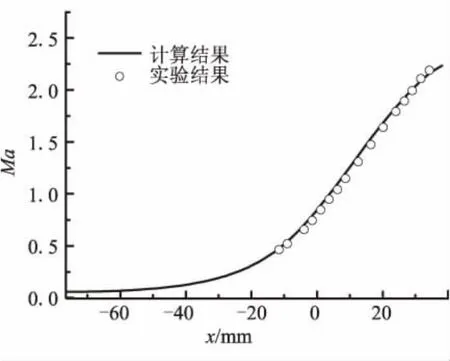
图3 轴线马赫数分布计算值与实验值Fig.3 Mach number along nozzle centerline

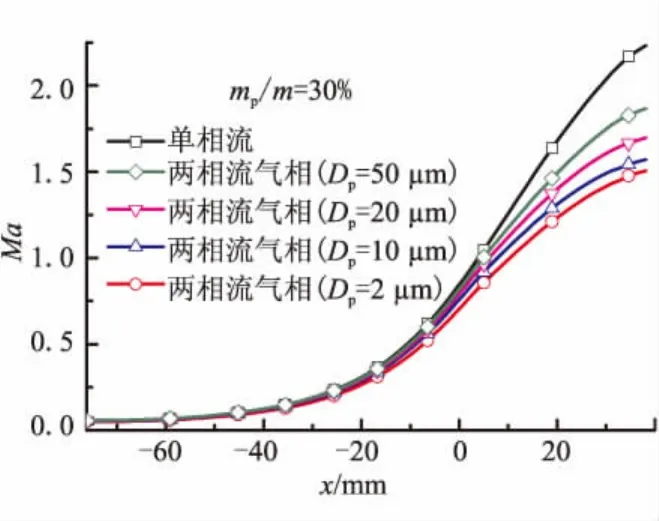
图4 单相流及两相流气相轴线马赫数(mp/m=30%)Fig.4 Gas phase Mach number of one-phase and twophase along nozzle centerline(mp/m=30%)

图5为Dp=2 μm时，单相流和不同mp/m的两相流气相马赫数沿轴向的分布。两相流的气相马赫数均小于单相流的马赫数，当比较 2、10、20、50 μm 4 种颗粒时，可看出随着Dp的增大，两相流气相马赫数逐渐增大，即小颗粒对气相的影响要大于大颗粒。当Dp相同时，随着mp/m的增大，两相流气相马赫数逐渐降低，即颗粒质量分数越大，对气相影响越大。

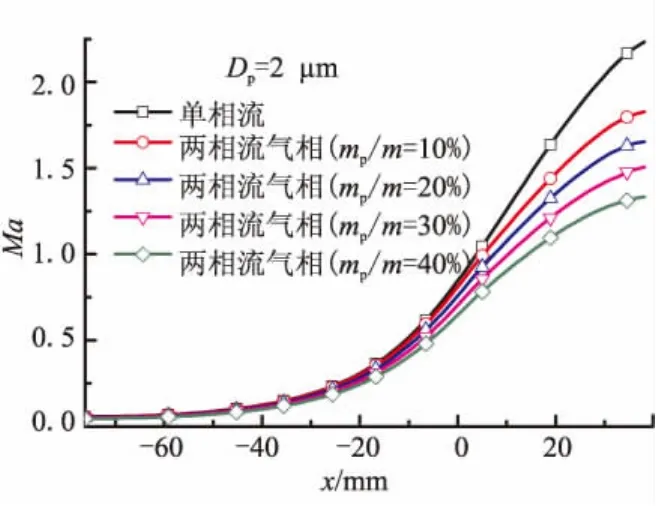
图5 单相流及两相流气相轴线马赫数(Dp=2 μm)Fig.5 Gas phase Mach number of one-phase and twophase along nozzle centerline(Dp=2 μm)

通过以上计算可看出，利用此方法对文献［1］和文献［6］中的JPL喷管进行计算得出的结果与实验结果及文献计算的结果是相同的。因此，利用该方法计算两相流问题是可靠的。

2.2 JPL喷管两相流计算

用此计算方法对喷管气固两相流进行计算，选取Dp分别为 1、2、3、4、5、6、7、8、9、10、15、20、30、50 μm的14种颗粒，在mp/m分别为10%、20%、30%、40%的情况进行计算，入口总温T0=3 300 K，计算结果如下:

图6～图8分别为喷管出口轴线点处的气相速度、马赫数、温度随着Dp及mp/m的变化，其中Dp=0 μm代表单相流的情况。

在相同mp/m情况下，喷管出口轴线点处气相速度和气相马赫数随着Dp的增大先减小、后增大，但均小于单相流的速度和马赫数，气相温度随着Dp的增大先增大、后减小，但均大于单相流的温度，即两相流损失随着Dp的增大先增大、后减小。此模型中，Dp=2 μm时，气相速度和气相马赫数最小，气相温度最大;对于mp/m=30%的情况，当Dp=2 μm时，气相速度为1 405 m/s，马赫数为 1.46，温度为 2 318 K。

在相同Dp的情况下，喷管出口轴线点气相速度和气相马赫数随着mp/m的增大而减小，喷管出口气相温度随着mp/m的增大而增大，即两相流损失随着mp/m的增大而增大。对于Dp=2 μm的情况，mp/m从10%增大到40%时，气相速度从1 589 m/s减小到1 301 m/s，马赫数从 1.75 减小到 1.31，温度从 2 044 K增大到2 058 K。

图9为mp/m=30%时，不同Dp的气相湍流动能k沿轴向的分布;图10为Dp=2 μm时，不同mp/m的气相湍流动能k沿轴向的分布。

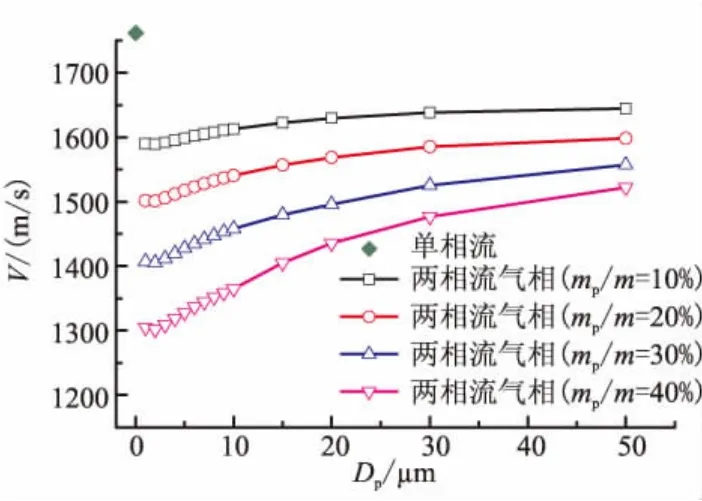
图6 喷管出口轴线点处气相速度Fig.6 Gas phase velocity of one-phase and twophase at the axis point of outlet of nozzle

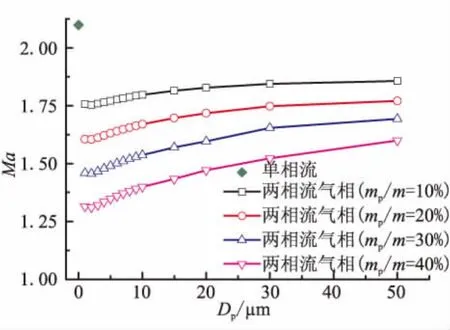
图7 喷管出口轴线点处气相马赫数Fig.7 Gas phase Mach number of one-phase and twophase at the axis point of outlet of nozzle

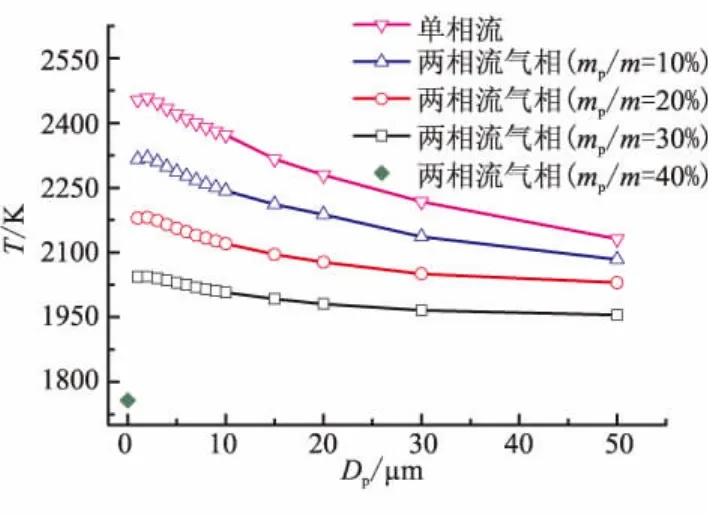
图8 喷管出口轴线点处气相温度Fig.8 Gas phase temperature of one-phase and twophase at the axis point of outlet of nozzle

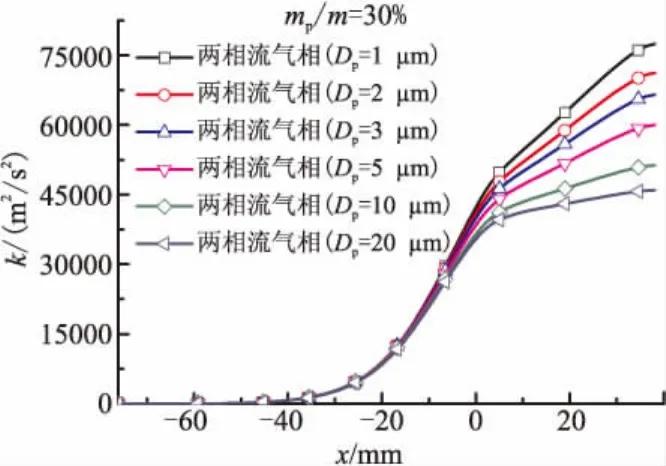
图9 气相湍流动能沿轴向的分布(mp/m=30%)Fig.9 The k of gas phase along nozzle centerline(mp/m=30%)

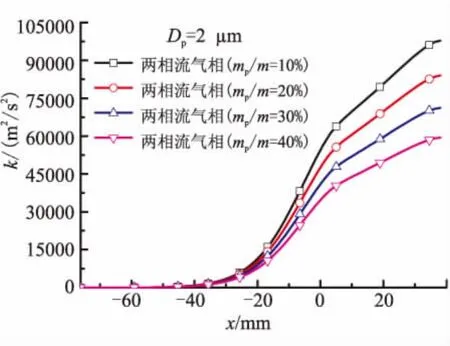
图10 气相湍流动能沿轴向的分布(Dp=2 μm)Fig.10 The k of two-phase along nozzle centerline(Dp=2 μm)

对于mp/m=30%的情况，当Dp从1 μm增大到20 μm时，气相的湍流动能k从77 409 m2/s2下降到45 902 m2/s2;对于Dp=2 μm的情况，当mp/m从10%增大到40%时，气相的湍流动能k从97 806 m2/s2下降到59 377 m2/s2。颗粒粒径越小，气相的湍流动能越大，气相和颗粒相的混合越均匀，相互之间的动量和热量交换越充分;颗粒质量分数越大，气相的湍流动能越小，两相混合均匀度减小，虽然这会使气相和颗粒相之间的动量和热量交换减弱，但质量分数越大，颗粒数目越多，颗粒的比表面积越大，颗粒与气相的接触越多，两相间的交换就越多，这一因素占对气相影响的主要方面。

图11为两相流中颗粒在喷管中的滞留时间。对于mp/m=30%的情况，当 Dp从 1 μm 增大到 50 μm时，颗粒在喷管中的滞留时间从 0.70 ms增大到1.30 ms;对于 Dp=2 μm 的情况，当 mp/m 从 10%增大到40%时，颗粒在喷管中的滞留时间从0.62 ms增大到0.77 ms。颗粒的粒径和质量分数越大，其在喷管内的滞留时间越长。这是因为颗粒粒径越大，其随流性越差，速度越小，因此在喷管内的运动时间长;颗粒质量分数越大，单位体积内颗粒的数目越多，因此颗粒能达到的速度越小，在喷管内的运动时间越长;滞留时间的增长，会使气相和颗粒相之间交换时间增长，动量及热量的交换越多。

从颗粒相对气相速度、马赫数和温度的影响可看出，颗粒粒径引起的两相流损失并不是单调的随着颗粒粒径的增大而减小［6－8］，或随着颗粒粒径的增大而增大［9－11］。在相同颗粒质量分数的情况下，颗粒粒径越小，数目越多，比表面积越大，颗粒与气相的接触面积越大，其间的动量与热量交换越多，同时颗粒粒径越小，两相中气相的湍流动能越大，相互间的交换也越充分;另一方面，颗粒的粒径越大，速度越小，在喷管内的滞留时间越长，与气相的作用时间越长，两相间的动量及热量的交换越多;因此，颗粒对气相造成的损失的大小是这两方面共同作用的结果，本模型中，颗粒粒径对两相流损失的影响随着粒径的增大而先增大、后减小。粒径约为2 μm的颗粒对两相流造成的损失最大。

颗粒质量分数造成的气相动量和热量损失随着颗粒质量分数的增大而增大，这是因为随着颗粒质量分数的增大，单位体积内颗粒数目增多，气相传给颗粒相的动量和热量交换越多，自身损失越大。图12为以速度计算的两相流喷管膨胀效率。可看出，两相流的喷管膨胀效率随着Dp的增大先减小、后增大，随着mp/m的增大而逐渐减小。对于mp/m=30%的两相流中，Dp=2 μm 时，喷管膨胀效率最低，约为 0.80，Dp=50 μm时，喷管膨胀效率约为0.88;对于Dp=2 μm的情况，当mp/m从10%增大到40%时，喷管膨胀效率从0.90减小到 0.74。

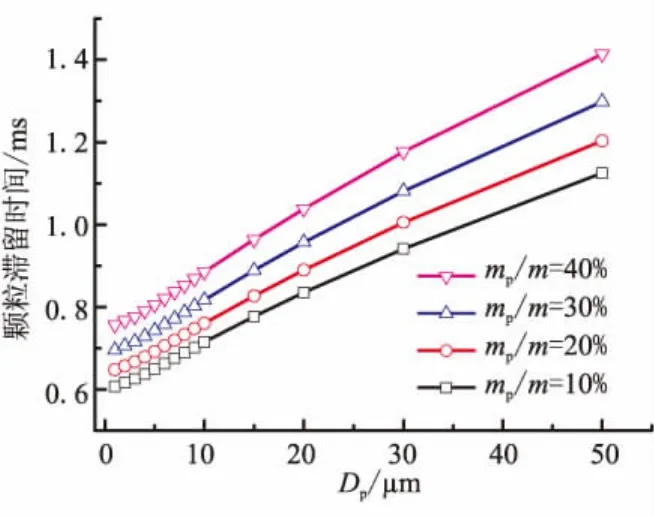
图11 两相流颗粒在喷管内的滞留时间Fig.11 Particle residence time of two-phase in nozzle

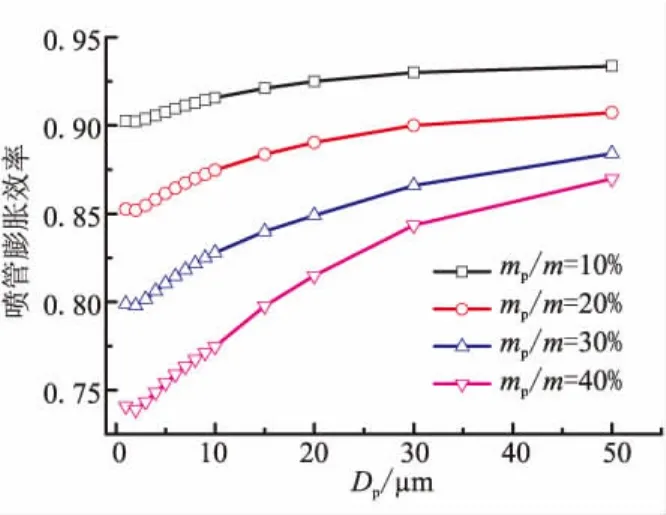
图12 两相流喷管的膨胀效率Fig.12 Nozzle expansion efficiency of two-phase flow

2.3 某火箭发动机喷管计算

利用该计算方法对另一固体火箭发动机喷管模型进行计算，网格如图13所示。

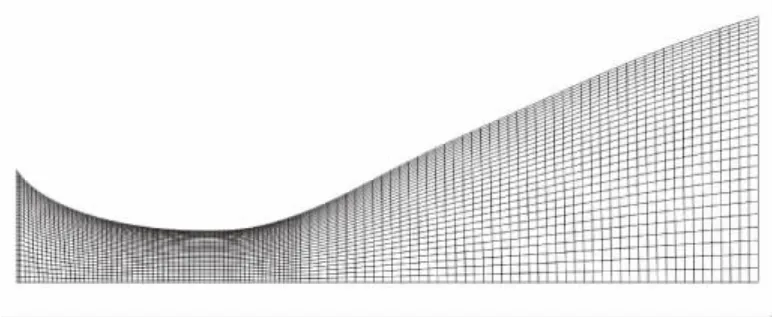
图13 计算模型网格划分Fig.13 Calculation nozzle grid

图14～图16分别为喷管出口轴线点处的气相速度、马赫数及温度随着Dp以及mp/m的变化。其中，Dp=0 μm代表单相流的情况。

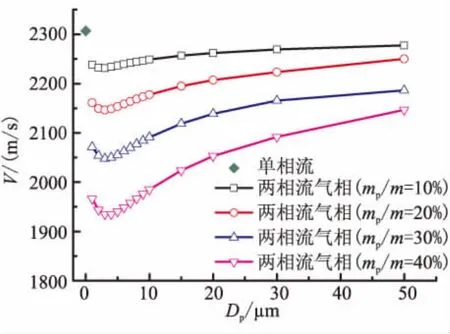
图14 喷管出口轴线点处气相速度Fig.14 Gas phase velocity of one-phase and twophase at the axis point of outlet of nozzle

图15 喷管出口轴线点处气相马赫数Fig.15 Gas phase Mach number of one-phase and twophase at the axis point of outlet of nozzle

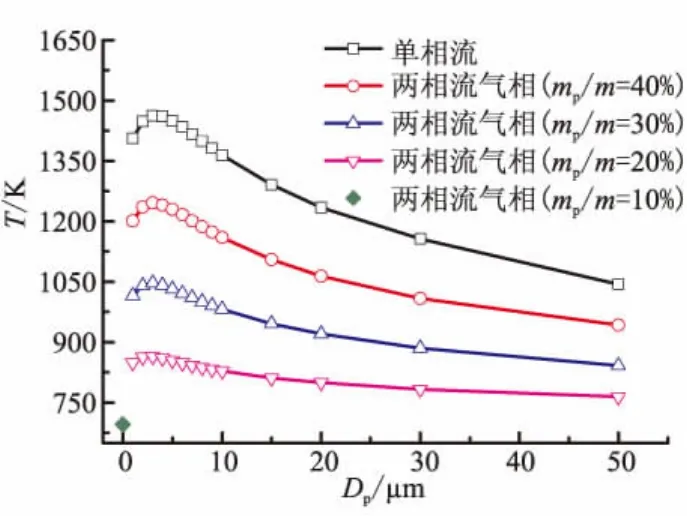
图16 喷管出口轴线点处气相温度Fig.16 Gas phase temperature of one-phase and twophase at the axis point of outlet of nozzle

从图14～图16中计算的气相速度、马赫数及温度可看出，2.3节计算出的结果与2.2节计算出的结果是相同的，本模型中，两相流的损失随着颗粒粒径的增大先增大、后减小，且粒径约为3 μm的颗粒造成的两相流损失最大。由2.2节和2.3节的2个模型计算出的结果还可知，对两相流造成最大损失的颗粒粒径是不同的，即颗粒粒径对两相流造成的损失的大小还与喷管的结构有关。

3 结论

(1)两相流的损失随着颗粒粒径的增大，并不是单调增大或者单调减小的;颗粒粒径越小，比表面积越大，颗粒与气相的接触面积越大，同时气相的湍流动能越大，其间的动量、热量交换越多;颗粒粒径越大，其速度越小，在喷管内的滞留时间越长，与气相的作用时间越长;颗粒粒径造成两相流损失的大小是这两方面共同作用的结果。本文2.2节中，2 μm的颗粒造成的两相流损失最大，对于颗粒质量分数为30%的情况，喷管的膨胀效率约为0.8。

(2)颗粒粒径造成两相流损失的大小与喷管的结构有关;本文2.2节中，粒径为2 μm的颗粒造成的两相流损失最大，而2.3节中，粒径为3 μm的颗粒造成的两相流损失最大。

(3)颗粒相的质量分数越大，造成的两相流损失越大;本文2.2节中，对于颗粒粒径为2 μm的情况，当颗粒质量分数从10%增大到40%时，喷管膨胀效率从0.90 减小到 0.74。

［1］Cuffel R F，Back L H，Massier P F.Transonic flowfield in a supersonic nozzle with small throat radius of curvature［R］.AIAA 1969-7.

［2］张宏安，叶定友，侯晓.固体火箭发动机凝聚相微粒分布研究现状［J］.固体火箭技术，2000，23(3).

［3］Hwang C J，Chang G C.Numerical study of gas-particle flow in a solid rocket nozzle［R］.AIAA 87-2168.

［4］何洪庆，周旭.固体火箭发动机燃烧室中的颗粒轨迹［J］.推进技术，1999，20(5).

［5］于勇，刘淑艳，张世军，等.固体火箭发动机喷管气固两相流动的数值模拟［J］.航空动力学报，2009，24(4).

［6］Chang I S.One-and two-phase nozzle flows［R］.AIAA 80-0272.

［7］李东霞，徐旭，蔡国飙，等.火箭发动机气体-颗粒两相流双流体模型研究［J］.固体火箭技术，2005，28(4).

［8］于勇，张夏，陈维.用双流体模型模拟超声速气固两相流动［J］.航空动力学报，2010，25(4).

［9］刘静，徐旭.随机轨道模型在喷管两相流计算中的应用［J］固体火箭技术，2006，29(5).

［10］严红，何洪庆.喷管二维跨声速两相湍流流场的数值模拟［J］.推进技术，1999，20(5).

［11］王元有.固体火箭发动机设计［M］.北京:国防工业出版社，1984.

(编辑:崔贤彬)

Effect of particle of wide-ranged sizes on gas expansion

LIU Jia-ning1，GAO Ye1，LIU Ping-an1，ZHANG Xi-feng2
(1.Department of Aerospace Engineering，Harbin Engineering University，Harbin 150001，China;2.North Hua＇an Industrial Group Co.，Ltd.，Qiqihaer 161046，China)

A two-fluid model was applied to simulate two-phase flow in two SRM nozzles.The interactional mechanism of gas phase and particle phase was studied.The effect on gas phase expansion in nozzle was studied under different particle sizes and different particle mass percentages.The results indicate that the loss of two phase flow caused by particle sizes is the combined product of the specific surface area of particles，turbulent kinetic energy of gas phase and particle residence time in the nozzle.The loss of two phase flow increases first and then decreases with the increase of particle sizes，while increases all along with the increase of particle mass percentages;In JPL nozzle，2 μm-diameter particles caused the most loss of two phases，increasing from 10%to 26%when the particle mass percentage ranges from 10%to 40%.

nozzle;two-phase flow;two-fluid model;particles;gas phase

V435

A

1006-2793(2014)06-0804-05

10.7673/j.issn.1006-2793.2014.06.012

2014-01-08;

2014-02-27。

国家自然科学基金(11372079)。

刘加宁(1989—)，男，硕士，主要从事火箭发动机内流场研究。E-mail:ljnzf123@126.com