基于流场函数的变刚度层合板铺放设计①

牛雪娟，杨 涛，杜 宇

(1.天津工业大学机械工程学院，天津 300387;2.天津市现代机电装备重点实验室，天津 300387)

基于流场函数的变刚度层合板铺放设计①

牛雪娟1，杨 涛1，杜 宇2

(1.天津工业大学机械工程学院，天津 300387;2.天津市现代机电装备重点实验室，天津 300387)

文章提出了一种新的变刚度铺层轨迹设计方法，即采用一对互相共轭的标量场函数实现复合材料变刚度铺层的轨迹定义和铺层设计。最后，通过有限元建模和算例对比方法，对直线铺放层合板和变刚度铺放层合板进行压缩特征值屈曲分析和非线性屈曲分析，得出变刚度铺放层合板的屈曲特性比直线铺放层合构件提高约23.62%，y方向的屈曲变形位移减小为直线铺层构件的59.47%，大幅度提高了构件的抗压缩屈曲特性，同时也验证了该设计方法的可行性和实用价值。

变刚度铺放;标量场函数;正交铺层;压缩屈曲分析

0 引言

作为飞机结构基本构件的复合材料层合板承受着各种载荷，只有对其进行合理的铺层设计，才能保证构件在各种规定载荷下的强度和刚度要求。传统的复合材料层合板多采用平行顺直纤维铺放成型，且为了简化设计和施工的工作量，工程中经常采用0°、90°和±45°铺层方向。此类层合板在承受面内压缩、剪切作用时，容易发生失稳破坏［1］。铺层内纤维取向的连续变化的铺放方法，可改变载荷在铺层平面内的分布，造成层合板上不同空间位置的刚度不同。这种变刚度的铺层方法可能会导致局部强度和刚度的降低，但可有效地提高层合板的整体结构性能，如屈曲载荷和破坏强度［2］。另外，变角度的铺放方法可通过调整内在载荷分布，避免应力集中［3］。

Hyer［4］最早提出用曲线铺放来增强层合板力学性能，采用分段连续轨迹，铺放角度为主应力方向。Negendra等［5］最早提出在整个薄板上构建完整的3次NURBS铺放轨迹，并采用有限元分析的方法，验证了Hyer［4］的说法。Gürdal等［6］采用先进的铺放设备实现了变刚度复合材料的首次制备，并提出了变刚度复合材料的概念，采用角度沿几何轴线性变化的曲线来定义铺放参考轨迹，并利用铺放头铺放出了变刚度层合板［7］，通过实验测试证明了变刚度层合板的承载能力明显优于传统的直线铺放层合板［8］。后来 Lopes［9］和Groh［10］等对变刚度层合板的剪切特性和失效特性进行研究，证明变刚度铺放成型的层合板的弯曲强度比直线铺放的层合板提高了56%。

国内对于变刚度铺放的研究相对较少，但已开始起步。秦永利［11］对纤维曲线铺放的变刚度复合材料层合板的研究进展进行具体的介绍。马永前［12］和赫晓东［13］用ABAQUS对Gürdal提出的变刚度复合材料层合板进行建模计算，验证在面内受力情况下，变刚度层合板的屈曲载荷比直线铺层结构提高14%。富宏亚等［14］根据零件外形数据信息，实现了非可展回转外壳类零件的变角度轨迹规划。杨涛等［15－16］对复合材料的变刚度铺放进行长时间的研究，并发表多篇相关论文。

本文采用传统直线铺放得到的准各向同性层合板作为基准板，与基于流函数的变刚度铺放的层合板的压缩屈曲特性进行对比。由于基准板每铺层的纤维角度与变刚度层合板在相应铺层上的纤维取向主方向一致，且基准板和变刚度板等厚，二者具有可比性，所得的对比结果具有可信的参考价值。

1 基于流场函数的曲线铺放轨迹表示方法

1.1 有势流动的标量场函数

由于流场的流函数与势函数是一对共轭函数，知道其中一个，另一个便可确定。这为本文所提的用流线簇和势线簇来规划一对正交铺层的轨迹提供了很大便利。

1.2 有势流动的标量场函数

通过离散流函数和势函数，可在流场中绘制等势线蔟和流线簇构成的流网。其中，流场中的流线簇可表达为

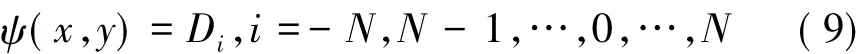
式中 N为流场中流值为正的流线簇的数目;Di为实常数，表示第i条等流线对应的流函数值。

由于流函数和势函数相对于原点均对称的，进行轨迹规划时，只需规划出流值为正的流线即可。相邻流线数值差δi=Di+1－Di，过原点的粗实线即为流值为0的流线。可通过改变式(6)中系数k的取值改变等流线的外形;通过改变相邻等流线流值差δi的取值，改变相邻等流线间距。

同样，流场中的势线簇可表达为

1.3 流线簇和等势线簇表示的正交铺层表示方法

根据有势流动理论，在任何一个网格点上流线和势线是正交的。基于这一性质，本文提出通过合理离散流场的流函数得到一组流线簇作为一个铺层(流线簇铺层)的铺放轨迹;通过合理离散流场的势函数得到一组势线簇作为另一铺层(势线簇铺层)的铺放轨迹。这两个铺层在力学上是相互平衡的，可构成一对正交铺层。通过改变相邻等流线流值差δi或相邻等势线势值差的取值改变同一铺层中相邻铺放轨迹间距，进而控制相邻轨迹的重叠率。在同一个铺层中，不同相邻流线间的流线差值可不同。

为了方便表示，这里将流场表示的一对互相正交的一对铺层(流线簇铺层和势线簇铺层)组合表示为⊥＜θ0，k＞。这里θ0为组成流场的直线均匀流的方向与流场x轴(即层合板长轴)的夹角;k为组成流场的点涡强度。

2 变刚度铺放轨迹的参数计算

2.1 纤维角度的计算

通过对式(9)所示的流线簇铺层轨迹方程两边求微分，可得到轨迹线上每个点位的切线方向，即铺放轨迹在该点位的纤维角度。同理，对式(10)所示的势线簇铺层轨迹方程两边求微分，可得到势线簇铺层上每个点位的纤维角度。

式(9)是平面流线的隐函数方程，根据隐函数的求导公式，可得出等流线ψι的切线矢量→Vψ的表达式如下:

2.2 相邻轨迹间距

流场中任一点位的梯度指向标量场增长最快的方向，且梯度模值为函数在该点的最大变化率。这一性质可用来求解平面标量场中两条等值线间的最小距离。对于变刚度铺层，利用梯度可求出相邻两铺放轨迹间的距离。由于流函数的梯度与势函数的梯度是正交的，流函数的梯度矢量方向为该点处等势线的切线方向，即流线簇铺层在该点处的梯度方向。同理，势函数的梯度矢量方向为该点处流线的切线方向，即势线簇铺层在该点处的梯度方向。

根据标量场中梯度的定义，流函数ψ的梯度矢量的表达式如下:

流线簇铺层中第i+1条铺带与第i条铺带间的距离di可表达为

其中，δi为沿着第i+1条流线的与第i条轨迹间的流值差。同理，势线簇铺层中第j+1条轨迹与第j条轨迹间的距离dj为沿着第j条等势线的梯度方向位移的距离，即

流场函数铺层设计方法充分发挥变刚度铺放的优势，通过添加最小距离约束的形式来对相邻轨迹间距进行限制。最小距离约束如式(23)所示:

式中 γ为铺放用的预浸带或纤维束宽度;ε1和ε2为宽度的容限率。

如果铺层中不允许出现间隙，则需设置ε1≥0。对铺层内各条轨迹线对应的流函数值进行设定，δj取‖▽ψj‖max·γ。采用这种方法可用尽可能少的轨迹数目铺放出变刚度层合板，从而提高了铺放效率和材料的利用率。

3 基于流标量场函数的变刚度层合板有限元分析

3.1 算例设计

试样的名义尺寸为508 mm×381 mm×3.81 mm(长×宽×厚)，共20层，每铺层的标准厚度为0.139 7 mm。铺放用纤维带宽度为4 mm。材料选用 AS4/9773，材料的工程常数如表1所示。

表1 AS4/9773炭纤维/环氧树脂基材料属性Table 1 AS4/9773 material system properties

为了与直线铺放方法和直线铺放方法进行对比，本文设计了两个算例:

直线铺放构件算例Z1:

Q1中除最外部2层为直线铺层外，其余铺层均为变刚度铺层。考虑到铺层厚度变化会引起力学性能的变化，为了与直线铺放方法进行有效对比，Q1中的变刚度铺层均采用无重叠方法进行铺放，即对相邻铺带间有重叠的区域的铺带进行剪裁，使得到的铺层为均匀等厚铺层。

3.2 基于流标量场函数的构件铺层轨迹设计

依照前面所述的有势流动的标量场函数构建方法，根据式(7)，针对每个奇数铺层(i=3，5，7…，17)构建流标量场函数:

根据式(8)，对每个偶数铺层(i=4，6，8…，18)构建势标量场函数:

Q1中变刚度铺层⊥〈30，80〉中流线簇铺层和势线簇铺层如图1所示。图中横线为流线簇铺层轨迹，竖线为势线簇铺层轨迹。由图1可清晰看出，在任一交点处等流线和等势线均正交。

图1 流线簇和势线簇构成的变刚度铺带轨迹Fig.1 Tape paths built by the streamlines

根据纤维角度的计算方法，得出如图2(a)所示的⊥〈30，80〉的流线簇铺层中零流线对应的铺叠轨迹上纤维角度随x坐标变化而变化的情况。最小值为17.71°，最大值为 29.50°。要计算相邻轨迹间距离需要先确定流场在轨迹的各个点位上梯度模值‖▽ψ‖。⊥〈30，80〉的流线簇铺层中零流线对应的铺叠轨迹上各点位的梯度模值为随x轴的变化曲线如图2(b)所示。

下面对Q1算例相邻轨迹间距离添加约束。这里设置ε2=0，即轨迹间最小距离为预浸带的宽度，即相邻轨迹间不会有间隙产生。为了将重叠率控制在25%以下，ε1数值取为 0.25。由式(23)知，相邻轨迹间距离有如下约束:

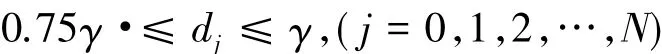
算例中铺放用的预浸带宽度γ=25.4 mm。利用该约束依次确定每条铺放轨迹对应流值。

由于流线簇与势线簇是完全共轭正交的，这里仅以流线簇铺层为例对铺层上各铺带的设计方法进行说明。零流值流线对应的铺带轨迹，这里定义为轨迹0。轨迹0与轨迹1间的距离d0为

要满足如上所述的最小距离约束，ψ1应满足如下2个条件:

由于‖▽ψ0‖最小值为 1.31，最大值为 1.64，为了尽可能提高材料的利用率，这里取‖▽ψ1‖为梯度模值的最大值1.64，此时ψ0=31.24。流场内流值最大值为 359.17。Q1中⊥＜30，80＞铺层采用共需 19 条铺放轨迹。由于流场中ψj是完全对称的，表2仅给出j≥0的流线簇对应的流值。

图2 ⊥＜30，80＞中零流线上铺带角度和梯度模值变化图Fig.2 Fiber angle and gradient magnitude distribution on the zero streamline of⊥〈30，80〉

图3给出了正交变刚度铺层⊥〈30，80〉中的流线簇铺层上的19条铺放轨迹的分布。图3中的棕色线条为轨迹0。轨迹1～9和轨迹－1～－9分别分布在轨迹0的两侧，且关于原点对称。

3.3 压缩屈曲特性分析

3.3.1 变刚度铺放对屈曲载荷优化机理分析

不同铺放曲线轨迹的变刚度铺层对屈曲载荷的优化机理是不同的。通过分析，可将变刚度铺放轨迹分为S形轨迹和反S形轨迹。S形轨迹指边界处的纤维角度大于中部的纤维角度;而反S形轨迹指边界处的纤维角度小于中部的纤维角度。

对于S形铺层，其对屈曲载荷的优化机理在于其对载荷的重新分配。具体分析如下:

层合板沿x轴方向应力合力可表达为

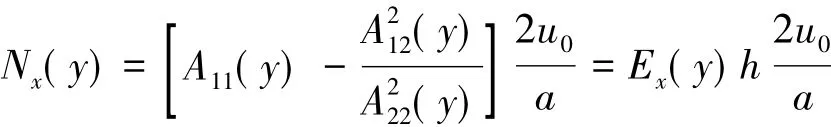
对于S形铺层，在层合板中部纤维取向与x轴正向间的夹角较大，Ex(y)较小，因而Nx(y)较小;在层合板边界处，纤维取向与x轴正向间的夹角较小，Ex(y)较大，因而Nx(y)较大。因此，变刚度的曲线铺放路径使得在x方向上施加的压缩载荷被在面内进行了重新分布，大部分载荷是由靠近边界的部分承受的，只有少部分集中在Y轴中部。正是由于将大部分载荷被转向层合板的横向边界，如图4所示，使得层合板的面外位移显著减小，从而使层合板的屈曲载荷得到提高。

表2 流线簇铺层上各条轨迹对应的流函数值ψjTable 2 Stream function values ψjon stream-layer

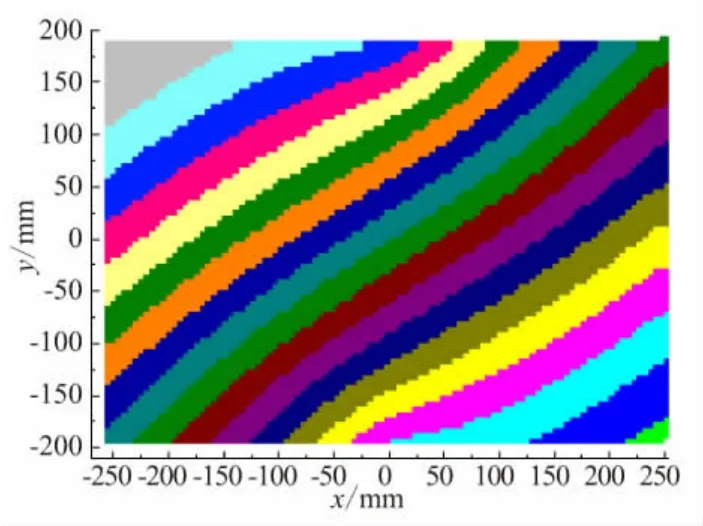
图3 流线簇铺层上各条铺带的分布Fig.3 Tapes distribution on the streamline layup

图4 一致压缩位移u0时纵向边界上Nx的分布［6］Fig.4 Distribution of Nxalong the y coordinate under uniform end shortening u0

对于反S形变刚度铺层，由于x方向中部的泊松比小于横向两侧的泊松比，在x方向施加压缩载荷时，在层合板中部形成局部横向拉应力。这种拉应力将与压缩屈曲载荷形成平衡，所以提高了层合板的整体屈曲载荷。

因此，无论是S形变刚度铺层还是反S形变刚度铺层，相较于直线铺层，屈曲强度都有所优化。3.3.2 复合材料构件有限元模型建立

网格类型为 S4R，网格单元大小为 5.08 mm×5.08 mm，网格数目为75×100，共 7 500个单元。模型的几何尺寸和边界约束情况如图5所示。下边界所有单元的6个自由度全部限制。上边界所有单元限制除y方向移动外的5个自由度。左边界和右边界的z方向位移和绕x轴的回转自由度被约束。

图5 层合板几何尺寸及边界约束情况Fig.5 Geometric dimension and boundary condition

3.3.3 特征值屈曲分析

特征值屈曲分析又称线弹性失稳分析，指结构在外载荷作用下，在原来的平衡状态之外，出现了第二个平衡状态。特征值屈曲分析问题可用式(27)进行描述:

式中 ［K］为刚度矩阵;［s］为应力刚度矩阵;λi为第i阶特征值;{ψ}i为第i阶位移特征矢量。

特征屈曲分析的目的是为了得到屈曲特征值λi和屈曲模态{ψ}i。将屈曲分析得到的第i阶屈曲载荷系数λi乘以外加载荷F，可得到第i阶屈曲极限载荷。

通过对直线铺层算例Z1和变刚度铺层Q1进行特征值屈曲分析，得出Z1和Q1的1～4阶屈曲的临界载荷如表3所示。表3中，各阶临界载荷的单位均为kN。由表3可知，当施加14.024 kN的压缩作用力时，直线铺放层合板发生屈曲失稳，而施加的17.337 kN的载荷时，变刚度铺放层合板才发生屈曲失稳。因此，Q1的一阶屈曲临界载荷比Z1的一阶临界载荷提高23.62%。

表3 Z1和Q1屈曲的临界载荷Table 3 the critical buckling loads of Z1＆Q1 kN

3.3.4 非线性屈曲分析

为了对带缺陷构件进行整体失稳性能进行分析，本文引入特征值屈曲模态作为初始几何缺陷进行非线性压缩屈曲分析。在非线性分析中，考虑到大变形效应，复杂应力状态下的破坏状态采用Von-Mises屈服准则来判别。非线性压缩屈曲分析中设定的初始缺陷与特征值模态间的关系如式(28)所示:

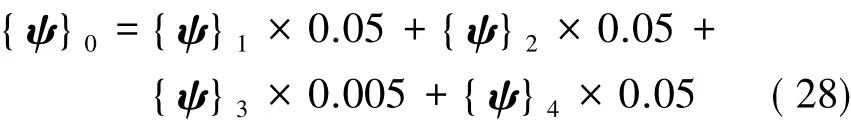
模型中施加的压缩载荷大小为20 kN。在该载荷作用下，Z1将进入二阶屈曲模态，而Q1仍处于一阶屈曲模态。面内各点位形变幅值如图6所示。

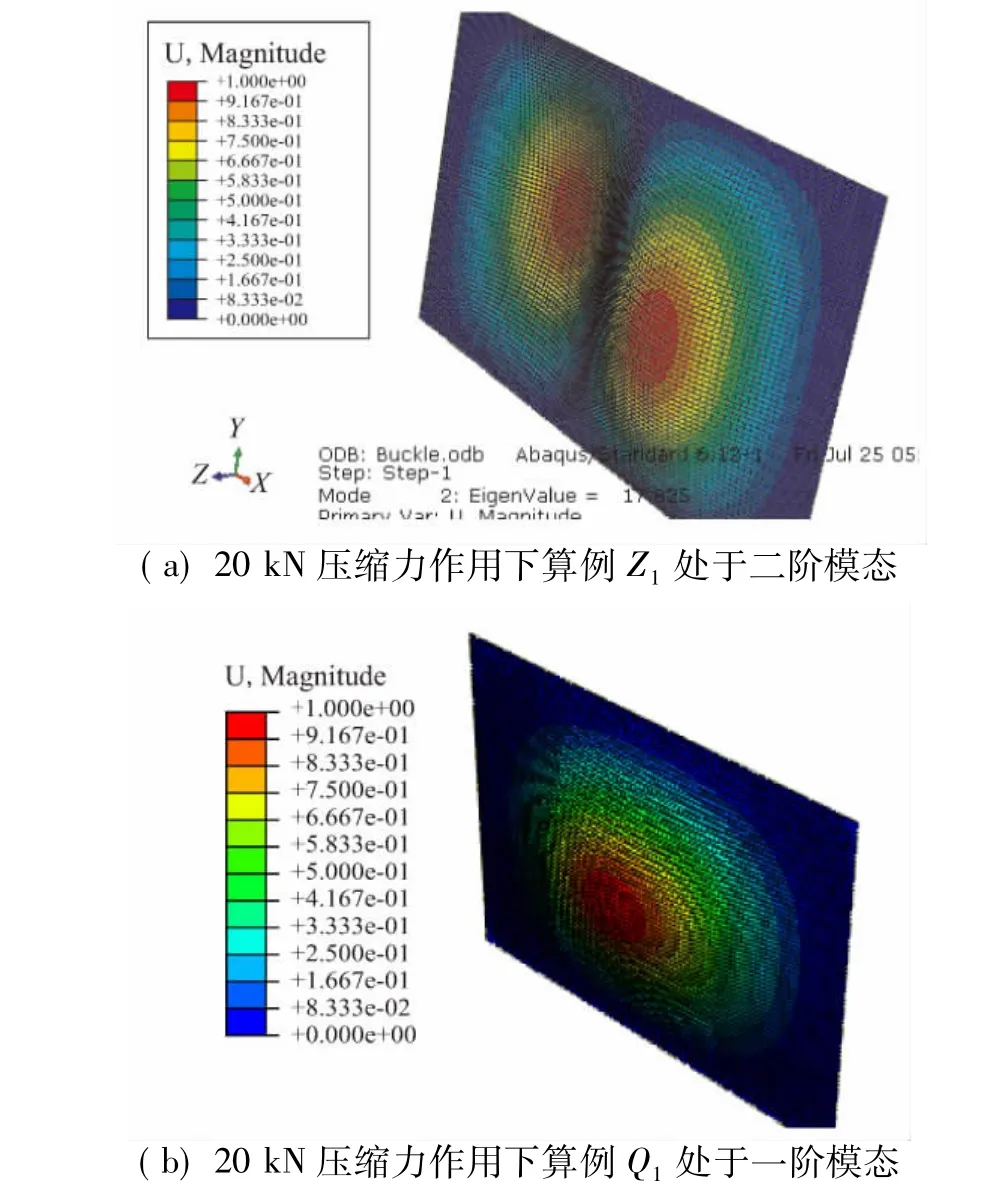
图6 20 kN压缩载荷下Z1和Q1的屈曲模态对比Fig.6 Buckling modes of Z1and Q1under 20 kN force

两层合板模型的非线性压缩屈曲分析结果如7所示。图7中，各个子图的横坐标x轴和纵坐标y轴分别为层合板的长度方向和宽度方向，单位均为mm;图7中，不同颜色表达的是给定方向上的不同位移值，单位为mm。

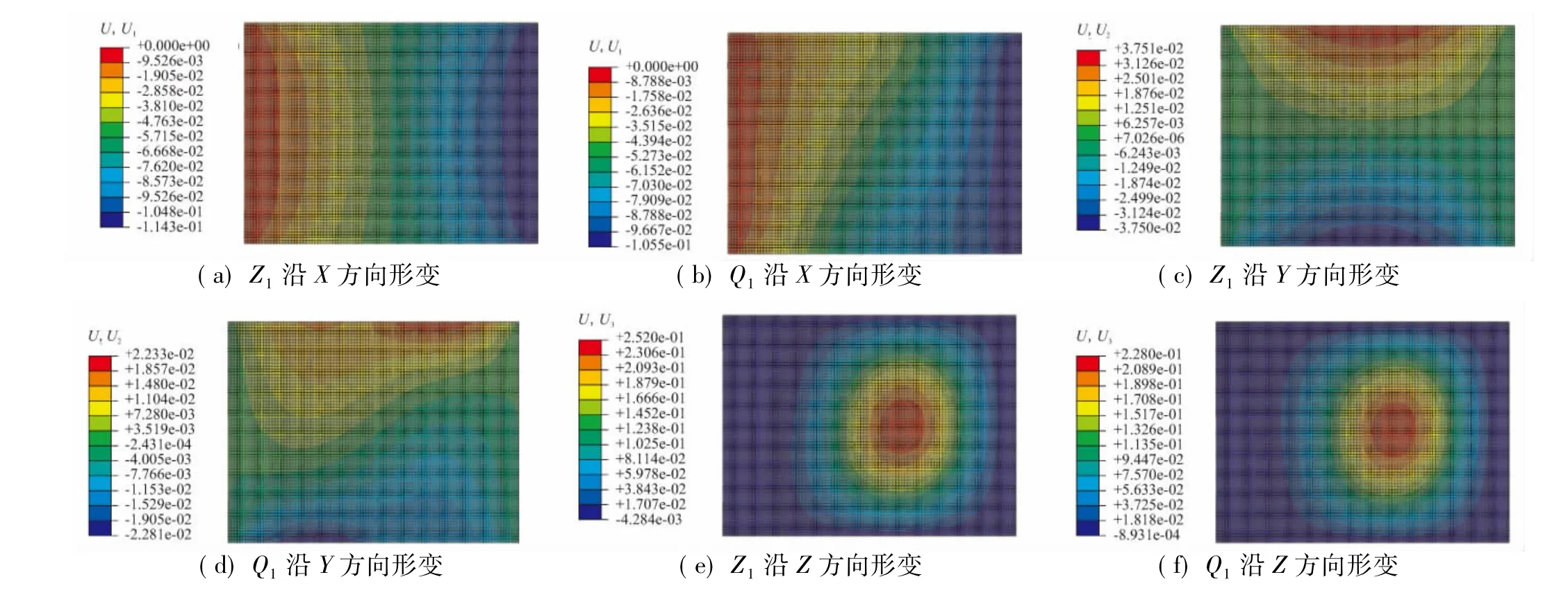
图7 算例Z1和算例Q1的非线性屈曲分析结果对比Fig.7 Nonlinear buckling analysis of Z1and Q1

在20 kN压缩载荷作用下，Z1和Q1上的各主方向位移的大小对比，如表4所示。由表4可知，通过本文所提方法改变纤维铺放角度，实现了y方向屈曲变形位移的大幅度改善。Q1的y方向的最大位移是Z1的59.47%，大幅度提高了复合材料层合构件的抗压缩屈曲特性。

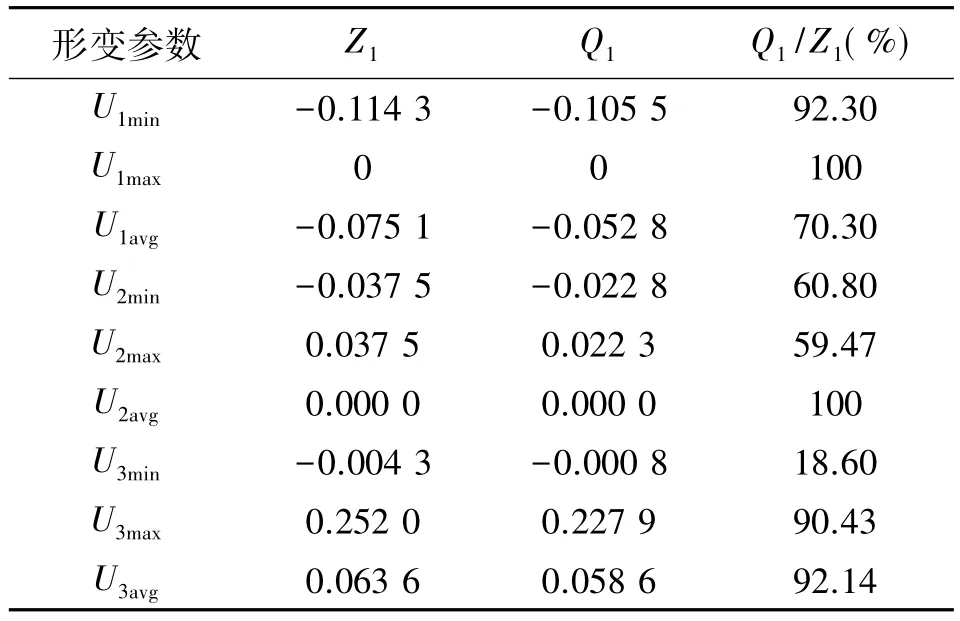
表4 Z1和Q1在20 kN压缩载荷作用下变形情况对比Table 4 Deformation of Z1＆Q1under 20kN force

4 结论

(1)基于流标量场函数实现变刚度正交铺层定义，不同于Güdal方法中通过计算参考轨迹平移曲线或平行曲线来获得其他轨迹，而是利用一个流场函数来计算整个铺层内所有轨迹进行规划设计，该方法有助于后续的轨迹优化工作。

(2)本文采用有势流场来构造一对互相共轭的流函数和势函数，通过合理离散这两个标量场函数获得互相正交的一组流线簇和势线簇，分别用来作为2个正交铺层的铺带轨迹，这2个铺层在力学上可实现平衡互补。

(3)根据流场函数利用解析法求解出相邻轨迹间的间距、铺层内任一点位上的纤维角度和铺层厚度，且可通过添加约束，对相邻轨迹间的距离进行控制。

(4)通过构建算例，采用有限元建模，将本文所提的变刚度铺放轨迹规划方法得到的等厚度变刚度层合板与传统的直线铺放层合板进行抗弯曲性能的对比，得出基于流场函数的变刚度层合板的抗弯曲性能比传统层合板提高了23.62%，y方向的屈曲变形比传统层合板减少了约40%。

［1］肖军，李勇，李建龙.自动铺放技术在大型飞机复合材料结构件制造中的应用［J］.航空制造技术，2008(1):1-4.

［2］Agnes Blom，盛蔼伦.纤维铺放、可变刚度复合材料:航宇结构的未来［J］.航空制造技术，2010(17):1-2.

［3］李俊斐，王显峰，肖军.开孔曲面自动铺放轨迹规划算法研究［J］.航空学报，2013，34(7):1716-1723.

［4］Hyer M W，Lee H H.The use of curvilinear-fiber format to improve buckling resistance of composite plates with central holes［J］.Composite Structures，1991，18(3):239-261.

［5］Nagendra S，Kodiyalam S，Davis J E.Optimization of tow fiber paths for composite design［J］.In Proceedings of the AIAA/ASME/ASCE/AHS/ASC 36th SDM Conference，1995:1031-1041.

［6］Gürdal Z，Tatting B F，Wu C K.Variable stiffness composite panels:Effects of stiffness variation on the in-plane and buckling response［J］.Compostites Part A:Applied Science and Manufacturing，2008，39:911-922.

［7］Wu K，Gürdal Z.Thermal testing of tow-placed，variable stiffness panels［C］//Proceedings of the AIAA/ASME/ASCE/AHS/ASC 42nd Structures，Structural Dynamics and Materials Conference，Seattle，WA，AIAA 2001，1190-1212.

［8］Wu K，Gürdal Z，Starnes Jr J.Structural response of compression-loaded，tow-placed，variable stiffness panels［C］//Proceedings of the AIAA/ASME/ASCE/AHS/ASC 43rd Structures，Structural Dynamics and Materials Conference.Denver，C O，AIAA 2002，1512-1535.

［9］Lopes C S，Gürdal Z，Camanho P P.Variable-stiffness composite panels:Buckling and first-ply failure improvements over straight-fibre laminates［J］.Computer and Structures，2008(86):897-907.

［10］Groh R M J，Weaver P M.Buckling analysis of variable angle tow，variable thickness panels with transverse shear effects［J］.Composite Structures ，2014(107):482-493.

［11］秦永利，祝颖丹，范欣愉.纤维曲线铺放制备变刚度复合材料层合板的研究进展［J］.玻璃钢/复合材料，2012(1):61-66.

［12］马永前，张淑杰，许震宇.纤维曲线铺放的变刚度复合材料层合板的屈曲［J］.玻璃钢/复合材料，2009(5):31-35.

［13］马洪涛，赫晓东.变刚度复合材料层合板的力学性能研究［D］.哈尔滨工业大学.2012.7.

［14］李玥华，富宏亚，韩振宇.两类非可展曲面零件自动纤维铺放变角度轨迹规划算法［J］.计算机辅助设计与图形学学报，2013(10):1523-1529.

［15］杜宇，杨涛，戴维蓉，等.纤维曲线铺放的变刚度复合材料损伤失效试验研究［J］.固体火箭技术，2013，36(6):826-830.

［16］戴维蓉，杨涛，牛雪娟，等.基于自由曲面构件的纤维变刚度铺放路径规划［J］.固体火箭技术，2014，37(2):262-268.

(编辑:薛永利)

Path planning of variable stiffness laminates based on the flow field function

NIU Xue-juan1，YANG Tao1，DU Yu2
(1.School of Mechanical Engineering，Tianjin Polytechnic University，Tianjin 300387，China;2.Advanced Mechatronics Equipment Technology Tianjin Area Major Laboratory，Tianjin 300387，China)

The variable stiffness layup method was put forward to optimize the component mechanical characteristics and failure resistance.A new variable stiffness path planning method was designed.A pair of scalar field functions，which are orthotropic at every intersect point，were used to define and plan the layup of laminate.Finally，the eigen value buckling analysis and nonlinear buckling analysis were conducted by means of FEM method，and the comparison between the straight fiber method and the variable stiffness method was done.The simulation results show that the buckling property can be improved by 23.62%，and the deformations in y-axis decrease to 59.47%of the original one.The capacity of anti-buckling of the specimen is greatly improved.The feasibility of the design method and practical value are verified.

variable stiffness tow-placing;scalar field function;orthogonal layup;compression buckling analysis

V254

A

1006-2793(2014)06-0848-08

10.7673/j.issn.1006-2793.2014.06.021

2014-09-01;

2014-09-16。

国家自然科学基金(11372220)。

牛雪娟(1977—)，女，博士，研究方向为复合材料工艺及制备。E-mail:niuxuejuan@tipu.edu.cn