导弹弹射系统中缓冲制动锥的轴向冲击特性①

姚保太，王汉平

(1.郑州机电工程研究所，郑州 450052;2.北京理工大学宇航学院，北京 100081)

导弹弹射系统中缓冲制动锥的轴向冲击特性①

姚保太1，王汉平2

(1.郑州机电工程研究所，郑州 450052;2.北京理工大学宇航学院，北京 100081)

针对壁厚线性变化制动锥的冲击力学特性，基于轴压力学模型，提出了等效速度概念，在综合考虑材料应变强化和应变率效应的条件下，按等效壁厚、等效速度条件下的分段能量等效原理得到了制动锥轴向冲击力学模型，并采用理论分析、有限元计算和实验研究相结合的方式研究了弹射系统中缓冲制动锥的冲击皱褶形成形态、冲击压缩量和缓冲力学特性，3种方法得到的结果基本一致，验证了所提模型的正确。所提出的制动锥轴向冲击力学模型可为制动锥的初步设计、实验规划以及武器系统的发射动力学分析提供参考。

弹射系统;制动锥;应变硬化;应变率效应;等效壁厚;等效速度;冲击

0 引言

薄壁圆柱壳作为缓冲吸能装置具有结构简单紧凑、制造加工方便、吸能效率较高、冲击变形规则且力学性能优良等特点，广为航空航天、武器工业和核电系统所使用［1－3］。针对薄壁圆柱壳的轴向压缩破坏模式及其力学特性的研究，早在20世纪60年代就已展开，Alexander等［4］基于材料的刚塑性假设利用固定塑性铰模型导出了轴对称渐进屈曲时的褶皱波长和平均轴压力公式，为本领域研究的开展奠定了基础;Johnson和 Reid［5］、Abramowicz和 Jones［6］在研究中考虑了几何效应，提出了有效压缩长度的概念，对Alexander模型进行了修正，获得了更合理的结果，同时还对冲击载荷作用下的材料应变强化和应变率效应进行了简化计算，将轴压特性推广到了轴向冲击;Wierzbicki和Bhat提出了移动塑性铰模型［7］，并据此模拟了载荷-位移曲线;此前的模型均基于管壁内翻或外翻，而试验表明，叠缩后的管壁是以一定比率分布在未叠缩管壁的两侧，据此，Wierzbicki等［8］修正了他们的模型，提出了偏心率效应，并给出了不同偏心率下的载荷-位移曲线，但假设偏心率对吸能效率没有影响;Singace等［9］改进了Wierzbicki等［8］的模型，认为吸能效率与偏心率有关，并给出了最优偏心率，同时通过实验验证了其结果［10］。而针对壁厚线性变化薄壁圆柱壳的研究，公开材料比较少，毕世华和王汉平［11］基于塑性铰理论，采用功能原理和能量守恒定律进行了理论探索，并借助有限元软件对轴压渐进屈曲特性进行了分析;王汉平和王忠峰［12－13］通过对上述各种模型进行对比验证，发现Wierzbicki等提出的不含偏心率效应的移动塑性铰模型与制动锥塑性变形模式更吻合，并在此基础上提出了等效壁厚概念，将该理论推广应用到了壁厚线性变化的薄壁圆柱壳的失效和轴压载荷分析，获得了较好的效果。壁厚线性变化的薄壁圆柱壳制动锥是提拉式导弹弹射装置中(如俄罗斯车载的S-300、S-400、道尔-M1和舰载的利夫和克里偌克等)的必备部件，其冲击力学特性是影响产品设计和使用安全性的关键，而当前对冲击特性的研究尚比较缺乏，尤其是在充分考虑材料应变硬化和应变率效应之后。工程上比较普遍的做法是采用有限元分析与实验测试相结合的模式来获取最佳设计，但这种方法计算量大、周期长，且数据分析和获取均不够直观，这给工程应用带来诸多不便。

本文在壁厚线性变化制动锥轴压理论的基础上提出了等效速度的概念，在综合考虑材料应变强化和应变率效应的条件下，按等效壁厚、等效速度条件下的分段能量等效原理得到了制动锥轴向冲击力学模型，该模型能准确预测冲击状态下制动锥皱褶个数、压缩量以及平均压缩力变化情况，可为此类制动锥冲击性能预测、冲击实验规划以及武器系统的发射动力学分析提供参考。

1 缓冲制动锥的轴向冲击理论

1.1 等壁厚圆柱壳的等速轴向冲击理论

制动锥在变形过程中受提拉杆的支撑，只能向外皱褶，这种失效模式与Wierzbicki等提出的不考虑偏心率效应的移动塑性铰模型更加吻合［7，12－13］，但也仅适用于拟静态的轴压过程，针对等速轴向冲击，由于材料应变率效应的存在，其轴向冲击载荷将会出现显著差异，因此需要对轴压模型予以修正，以包含因冲击而产生的应变率效应的影响。

根据Wierzbicki等的理论，圆柱壳的压皱半波长和平均压皱力为

式中 σ0为材料屈服极限应力;D、q为材料应变率相关的系数。

在静态σ0(ε0)的基础上乘上当量应变率d时的应变率效应系数就可获取应变率效应影响下的当量屈服应力σd，用σd替换式(2)中的σ0就可包含材料应变强化效应和应变率效应的影响。

1.2 壁厚线性变化圆柱壳轴向冲击模型

根据等效壁厚概念［12－13］，可得到各分段等效壁厚的形式如下:

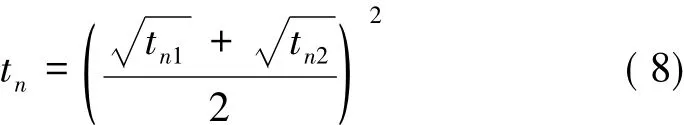
式中 n表示第n个褶皱;tn为第n个褶皱的等效壁厚;tn1为第n个褶皱薄壁端壁厚;tn2为第n个褶皱厚壁端壁厚。

在冲击过程中，提拉杆的速度是一个变化的量，为扩展利用等壁厚、匀速冲击模型，故根据应变率效应的应力影响系数与匀速冲击速度间的幂函数关系，利用功能原理和能量守恒定律就可获得应变率效应的当量应力影响系数即为皱褶形成始末的应力影响系数的算术平均，由此提出等效速度概念，即在皱褶形成过程中对应于应变率效应的当量应力影响系数的速度即为等效速度，其形式如下:

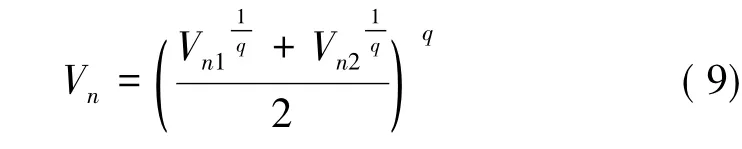
式中 Vn为形成第n个褶皱的等效速度;Vn1为第n个褶皱开始形成时的冲击速度;Vn2为第n+1个褶皱开始形成时的冲击速度。

根据功能原理、有效压缩量与皱褶波长的关系［3］可得

本段圆柱壳可看作壁厚为tn的等壁厚圆柱壳，圆柱壳的褶皱长可按等壁厚圆柱壳褶皱长公式求出:

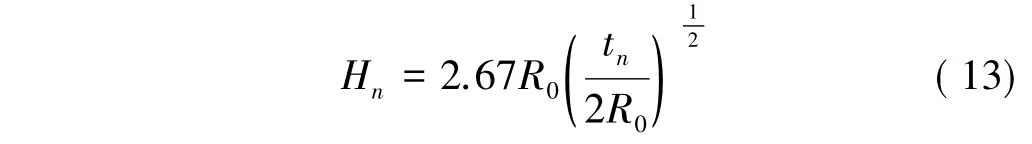
式中 Hn为第n个褶皱半波长。

另外，还存在一个已知的隐含条件，即壁厚变化楔形角α已知，且

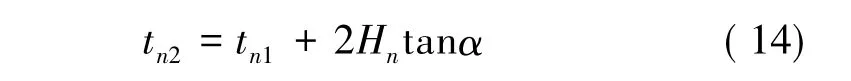
联立方程式(8)～式(14)，设定计算终止条件为Vn2≤0，采用递推的方式就可逐级求解每个褶皱的等效壁厚、等效速度、褶皱半波长、轴向冲击平均力、皱褶形成后的速度以及每个皱褶吸收的能量。

2 有限元仿真、实验研究和理论分析结果对比

为方便制动锥的变参数仿真和特性优化，本文使用ABAQUS的参数化建模方法将制动锥薄壁端厚度、厚壁端厚度、法兰半径、制动锥内径、上下法兰厚度、制动锥有效长度、单元最小尺度、冲击块质量以及冲击速度设置为参数，借助ABAQUS的关键字NODE、NGEN、NFILL、ELEMENT、ELGEN构建了制动锥参数化的轴对称有限元模型，并编写了PYTHON脚本，可实施实验设计(DOE)仿真;还对制动锥的材料进行了拟静态和动态实验，获取了材料的弹塑性本构模型。为了验证上述理论模型，对不同结构尺寸的壁厚线性变化圆柱壳、不同的冲击速度状况进行了冲击有限元分析［12，14］。同时还针对2款制动锥进行了不同速度的冲击实验，并对仿真计算、理论分析以及实验结果进行了对比分析。圆柱壳长度分别为250 mm和150 mm，内径40 mm，两端壁厚不同。为了方便描述，本文采用了圆柱壳长度和上下端壁厚值对圆柱壳进行了编号，如:“250-0624”表示上端壁厚为 0.6 mm，下端壁厚2.4 mm，长度为250 mm的圆柱壳。实验采用弹簧储能释放冲击台，由于受结构限制，对于25 kg的冲击物，该冲击台所能提供的最大出射速度为20 m/s。

因此，本文就250-0624件冲击速度为17、18、19、20 m/s和150-0513件冲击速度为16 m/s进行了实验。

2.1 褶皱数分析

图1是不同冲击速度条件下制动锥最终的变形情况和仿真结果的对比。从中不难看出，实验和仿真中，制动锥均在薄壁端形成皱褶，且同结构尺寸的制动锥压缩量和皱褶个数与冲击速度正相关。

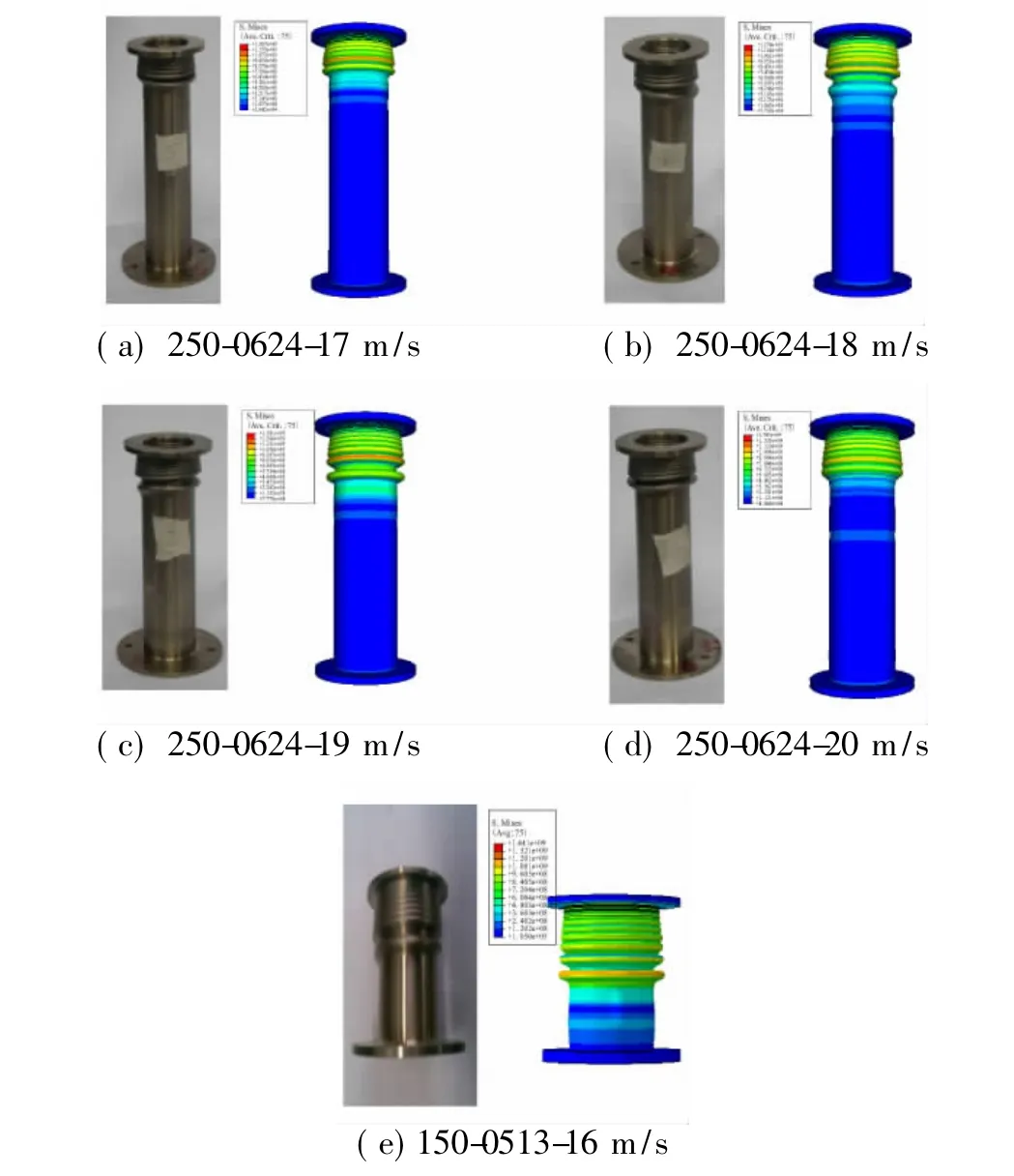
图1 不同试件在不同冲击速度情况下的变形仿真与实验结果对比Fig.1 Comparison of computational and experimental deformation under various impact velocities

表1数据表明，轴向冲击特性条件下将壁厚线性变化的缓冲制动锥按等效壁厚、等效速度分段等效简化后计算所得的褶皱数与有限元仿真以及实验结果一致。理论、仿真及实验结果均表明壁厚线性变化圆柱制动锥在受到轴向冲击时的最终轴向褶皱数随着冲击速度的增加而增多，且压缩量也相应增大，由于冲击速度差异不大，最终有些皱褶并未完全成形。

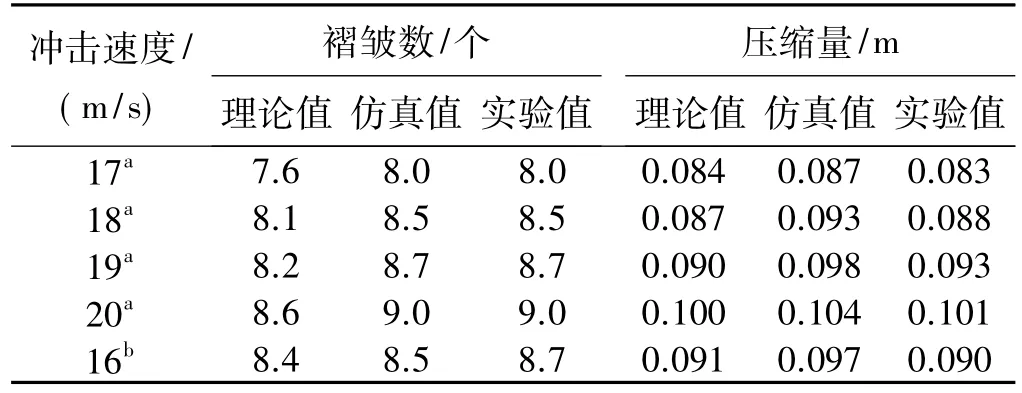
表1 不同冲击速度下试件的褶皱数和压缩量对比Table 1 Comparison of buckling waves and compression length under various impact velocities

2.2 轴向冲击平均力分析

冲击载荷作用下缓冲制动锥的缓冲制动时间较短，由于选用的传感器采样频率不够，同时传感器与有源放大器之间参数存在匹配问题，实验时未能很好记录到完整皱褶形成过程的缓冲载荷历程，但所记录到的最大载荷也具有一定的参考价值，表2是实验记录最大缓冲载荷与计算缓冲载荷的对比。

表2 不同冲击速度下250-0624件最大缓冲力的仿真与实验对比Table 2 Comparison of maximum impact loads under various impact velocities

考虑到仿真计算的皱褶波数以及冲击后制动锥的压缩量与实验结果吻合较好，本文在进行轴向冲击平均力分析时直接对仿真缓冲载荷-行程历程采用目标函数f(x)=A+B·xC进行了曲线拟合，同时将拟合曲线、仿真曲线和理论计算的轴向冲击平均力进行了对比，不同冲击速度条件下的对比情况见图2。

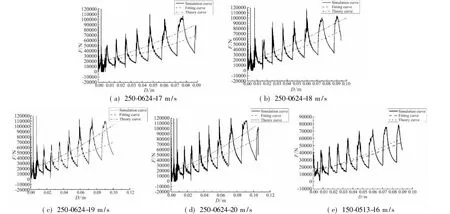
图2 不同试件在不同冲击速度条件下轴向平均冲击力理论计算与仿真结果对比Fig.2 Comparison of theoretical and FEA computational curves for linear thickness braking cylindrical shells under various impact velocity

由图2可看出，不同冲击速度条件下有限元计算 缓冲载荷拟合曲线与理论计算曲线基本吻合，但总体上理论计算值偏大。另外，高速摄像(尽管因采样频率不足，无法完整记录皱褶发展过程)和有限元仿真动画表明，冲击过程中制动锥的总体变形效果是薄壁端先出现褶皱，然后依次向厚壁端推进。仿真数据表明，在缓冲器刚开始承受冲击时，载荷存在较大的脉冲峰值，而随后轴向冲击载荷随褶皱向厚壁端推进而逐渐增大，且载荷在增大过程中还呈现出一定程度的波动特性，波动幅度也随壁厚增大而增大。

3 结论

(1)针对壁厚线性变化缓冲制动锥的冲击力学特性，提出了等效速度概念，并联立制动锥等效壁厚和有效压缩量概念，利用圆柱壳分段能量等效办法建立了圆柱壳的冲击力学模型;模型中综合考虑了材料应变强化和应变率效应的影响，使得模型具有更好的精度。

(2)通过材料动态试验获得的本构模型进行了理论分析、有限元计算和冲击实验的对比研究表明，制动锥皱褶数一致、冲击压缩量吻合、最大冲击载荷基本相符，这验证了等效速度和等效壁厚概念联立使用的制动锥冲击力学模型的可信性，该模型可用于制动锥的工程设计及其轴向冲击力特性的预测，也可用于提拉式弹射装置的弹射发射动力学的建模。

［1］诺曼·琼斯.结构冲击［M］.蒋平，译.成都:四川教育出版社，1994.

［2］余同希，卢国兴.材料与结构的能量吸收-耐撞性 包装安全防护［M］.华云龙，译.北京:化学工业出版社，2006.

［3］杜星文，宋宏伟.圆柱壳冲击动力学及耐撞性设计［M］.北京:科学出版社，2004.

［4］Alexander J M.An approximate analysis of the collapse of thin cylindrical shells under axial loading［J］.Q.J.Mech.，1960，13(1):10-15.

［5］Johnson W，Reid S.Metallic energy dissipating system［J］.Applied Mechanics Reviews，1978(31):277-288.

［6］Abramowicz W，Jones N.Dynamic progressive buckling of circular and square tubes［J］.Int.J.Impact Engng，1986，4(4):243-270.

［7］Wierzbicki T，Bhat S U.A moving hinge solution for axisymmetric crushing of tubes［J］.International Journal of Mechanic and Science，1985，28(3):135-151.

［8］Wierzbicki T，Bhat S U，Abramowicz W，et al.Alexander revisited—a two folding element model of progressive crushing of tubes［J］.International Journal of Solids and Structures，1992(29):3269-3288.

［9］Singace A，Elsobky H，T Y R.On the eccentricity factor in the progressive crushing of tubes［J］.International Journal of Solids and Structures，1995(32):3589-3602.

［10］Singace A，Elsobky H.Further experimental investigation on the eccentricity factor in the progressive crushing of tubes［J］.International Journal of Solids and Structures，1996(33):3517-3538.

［11］毕世华，王汉平，梁征.导弹垂直弹射过程中制动锥的动力学特性研究［J］.北京理工大学学报，2004，24(9):762-765.

［12］王忠峰.提拉杆式弹射系统缓冲制动锥力学特性研究［D］.北京:北京理工大学，2006.

［13］王汉平，王忠峰.导弹弹射系统中缓冲制动锥的轴压特性［J］.北京理工大学学报，2007，27(2):99-102.

［14］Karagiozova D，Alves M，Jones N.Inertia effects in axisymmetrically deformed cylindrical shells under axial impact［J］.International Journal of Impact Engineering，2000，24:1083-1115.

(编辑:吕耀辉)

Mechanical characteristics of the braking cylindrical shells of missile ejector under axial impact

YAO Bao-tai1，WANG Han-ping2
(1.Zhengzhou Mechano-Electronic Engineering Research Institute，Zhengzhou 450052，China;2.School of Aerospace Engineering，Beijing Institute of Technology，Beijing 100081，China)

For impact mechanical characteristics of the linear thickness braking cylindrical shells，a concept of equivalent velocity was proposed.Based on the energy equivalent principle of subsections under equivalent thickness and eguivalent velocity condition，an impact mechanical model of linear thickness braking cylindrical shells，which takes into account the strain hardening and strain rate effect of structural material，was built.The wrinkle creation forms，compress stroke and mechanical characteristics of the braking cylindrical shells of missile ejector under axial impact has been studied by means of theory analysis，FEM and experiment.Three methods get identical results，which verifies the correctness of the model.The theory model of linear thickness braking cylindrical shells can be used in the initial engineering design and experiment planning of the braking cylindrical shells and in the launching dynamics analysis of the weapon system.

missile ejector;braking cylindrical shell;strain hardening;strain rate effect;equivalent thickness;equivalent velocity;impact

TJ768.2

A

1006-2793(2014)06-0863-05

10.7673/j.issn.1006-2793.2014.06.023

2013-11-05;

2014-05-26。

姚保太(1976—)，男，高工，主要研究方向为兵器发射理论与技术。E-mail:yaobaotai@163.com

王汉平(1971—)，男，副教授。E-mail:whp161@bit.edu.cn