航天器舱体热密封结构多物理场耦合数值分析方法研究①
白瑜光,夏广庆,孙得川,高效伟
(1.大连理工大学 工业装备结构分析国家重点实验室,大连 116023;2.大连理工大学航空航天学院,大连 116023)
航天器舱体热密封结构多物理场耦合数值分析方法研究①
白瑜光1,2,夏广庆1,2,孙得川1,2,高效伟1,2
(1.大连理工大学 工业装备结构分析国家重点实验室,大连 116023;2.大连理工大学航空航天学院,大连 116023)
综合考虑航天器舱体外围高超声速流动、密封带及舱体结构传热以及密封结构内部的空腔流动传热,提出航天器高温热密封结构的瞬态多物理场耦合分析方法。利用改进型Van Driest变换方法进行高超声速流动环境预测,基于高斯-赛德尔分块迭代耦合方法完成一体化耦合计算方法。采用包含不同材料结构部件的复合结构,计算了0~200 s内有无密封塞两种情况下的各部分结构的瞬态热传导过程。结果表明,密封塞的使用可显著降低空腔内的最高温度,瞬态变化情况的考虑更加准确地反映了各部分结构部件及内部空腔的温度变化情况。该文的计算方法可广泛应用于航天器热密封结构的传热特性分析,可为火箭等航天器上的高温密封部件设计提供有效的数值分析工具。
多物理场耦合;热密封结构;瞬态热传导;Van Driest变换
0 引言
高温热密封技术应用广泛,是现代工业领域发展最为重要的技术之一[1]。对于一个国家最高科技水平象征之一的航天技术领域,高温热密封技术起着至关重要的作用,高温热密封结构是各种型号航天运载火箭及航天飞行器的关键零部件之一。美国Apollo航天器使用了大量密封技术来保障控制舱段和乘员舱段的正常工作[2];美国大力神-Ⅱ洲际导弹共使用了各种密封件340多项、900多处,且多数处于关键部位[3]。
航天领域比较常见的密封是舱体各舱段的连接部位、控制舵翼舵轴以及发动机内部位等。国内外已有的研究主要针对于密封材料本身,通过各种高温试验[4-5]及数值计算[6-7]得到密封材料的相关性能参数以及进行密封可靠性分析。随着航天器的速度不断提升,耦合数值计算的方法和应用不断发展,但目前常见的商用CFD软件或基于密度的求解器来进行高超声速流动分析,或基于压力的求解器来进行低速流动分析,可同时计算2种不同类型流动的软件及程序仍属少见。因此,综合考虑航天器热密封结构外围高超声速气动环境、密封材料传热传质以及密封结构内部空腔低速流动传热的瞬态一体化计算方法有待进一步探索。作者曾将一维高斯-赛德尔(Gauss-Seidel)分块迭代耦合算法[8]成功地发展至三维钝体气动弹性分析[9]及主动冷却发动机结构的热-流-固耦合分析[10]。
本文基于此方法进行高超声速环境下航天器舱体热密封结构的瞬态耦合传热分析方法研究。首先利用改进型Van Driest变换方法处理高马赫数外流场,然后基于高斯-赛德尔分块迭代耦合算法提出航天器舱体热密封结构的一体化数值分析方法,最后根据有无上密封塞2种情况对热密封结构模型进行计算分析。
1 计算方法
本文的计算方法涉及到热密封结构外围高超速气动环境、密封结构固体部件传热及结构内部空腔流动传热3部分的数值计算方法及最终的耦合计算方法。
1.1 高超声速流动的Van Driest转化方法
对于密封结构外围的高超声速流动,本文基于常见的雷诺平均方法求解可压缩N-S方程[11],同时结合Van Driest转换方程处理外围可压缩流动边界层[12],该方程的表达形式为(对数形式):

在固体壁面附近,整体近壁面动量方程可改写为

考虑气体为完全理想气体,此时边界层上的压力为恒定的,将式(7)代入式(2),可以得到“可压缩”速度的表达式:
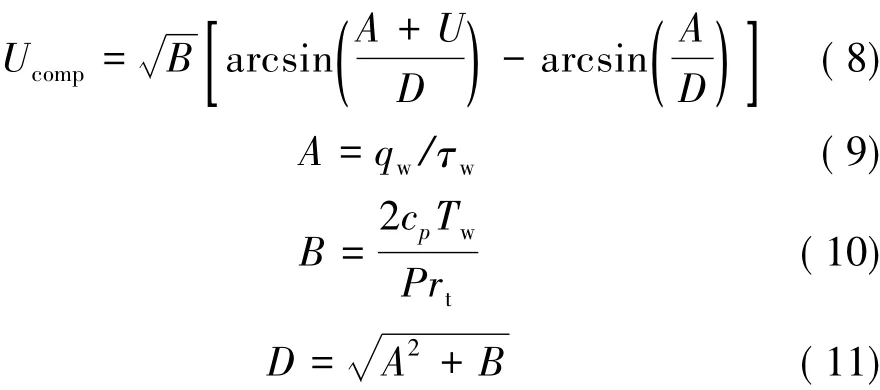
这些方程涵盖了可压缩流壁面函数的必要表达式。将式(2)重新整理可得

可以发现,只要得到θ+,近壁面速度、温度以及壁面温度和壁面热传导即可计算。根据Kader[13]提出的热壁面函数,可以将θ+改写为

将式(20)代入式(16),可得到θ+。这样壁面热传导和壁面温度就可以由式(15)得到。
1.2 固体结构传热计算公式
对于结构热分析,二维导热控制微分方程可写为
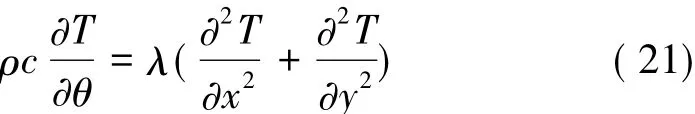
式中 左端表示固体微元热力学能的增量,右端表示导入微元的净热流量;T为温度;c为比热容;λ为热导率;θ为时间增量。
1.3 耦合算法
本项研究中主要利用高斯-赛德尔分块迭代耦合方法进行耦合算法的实现[9]:
假设存在一个待求解的流体-固体耦合问题,流体区域采用欧拉描述,记为Ωf;而结构区域一般采用拉格朗日描述,记为Ωs;它们存在共同的边界为∂Ωi=∂Ωf∩∂Ωs,在此共同的边界上发生流固耦合作用现象。
在交界面上存在位移等价条件(交界面∂Ωi在时间 t时位于 ξ+φ(ξ,t)处,ξ表示参考位置)。此外,交界面上相应的点还存在速度等价条件:
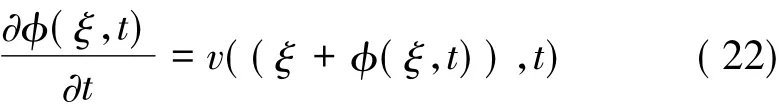
除了这些运动学关系,交界面上还有力平衡关系:
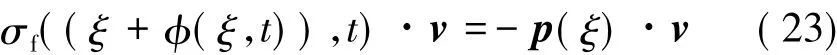
式中 v为交界面上∂Ωi的法向量。
下面对流体和固体两区域分别进行离散化求解。假定每个子问题在求解时为时间隐式(处于计算稳定性的考虑,也希望所有时间步中均为时间隐式)。仍然将离散后的流场速度矢量记为V,相应的压力也仍然记为p。离散后的结构位移矢量记为u,离散后的结构速度矢量则为因此,从时间步n到n+1需要求解离散的增量N-S方程和结构方程,它们可统一写成如下形式:
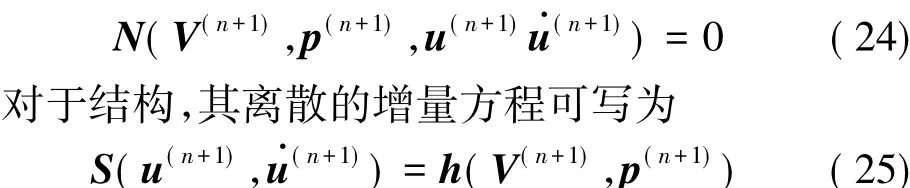
这里只写出时间步n+1的待解量,其他量均假设为已知。可以发现,在时间步n+1时流体的表达方程(24)显式依赖于结构的位移和速度;同时,从式(25)可看到在时间步n+1时流体施加于结构的荷载h(V(n+1),p(n+1))同样依赖于流体的速度和压力,两式是相互耦合的。

方程(24)和方程(25)可用直接耦合解法或者分块迭代方法求解。直接耦合解法需要联合系数阵和专用求解器,所以实行的难度比较大。分块迭代方法可以使用已有软件的分离求解器。可通过结合分块高斯-赛德尔耦合法则的已有求解器求解N-S方程,先求解变量ɑ再求解变量b。迭代公式为
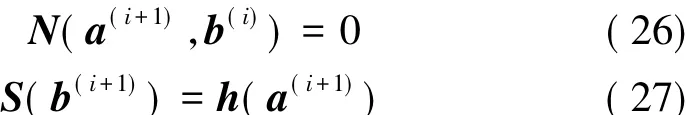
式中 i为迭代步数。
式(26)是非线性的,式(27)根据所使用的结构模型可是线性的或者是非线性的,为了一般性考虑,也认为其是非线性的。这就需要使用线性化方法。将其进行线性化迭代后可表示成:
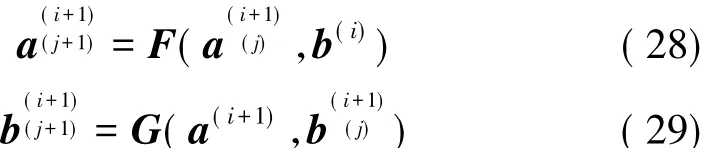
式中 j为线性化迭代步数。
根据式(28)和式(29)求解流-固耦合问题或者非线性问题时,对i和j进行两层迭代。与用直耦法求解式(24)和式(25)相同,每一时间步在进行迭代时都要检验其收敛性。将两层迭代合并写成:式中 k为合并迭代步数。
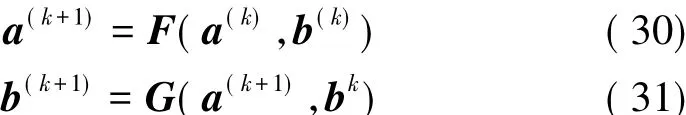
式(30)和式(31)的求解过程可通过CFD程序以及结构分析程序实现。
对于本文的多物理场耦合问题,还需考虑耦合传热问题,因此在耦合边界上要保证温度的正确传递,通常的方法有:

其中,区域I为流体或固体;区域II为流体。例如首先对区域II进行求解,得到耦合边界上的局部热流密度和温度梯度,然后再求解另一个区域I,得到耦合边界上新的温度分布,再以此分布作为区域II的输入,重复上述计算直到收敛或者达到指定计算时间。
本文基于网格的量,传递到另一个场的过程为面到面的传递过程,采用整体守恒插值方法(保留热通量及力的量)。如图1所示,在整体守恒插值中,发送端的每一个节点X映射到接收端的一个单元上,因此发送端的传递变量就分成2个量,这2个量添加到接收器节点中。节点4处的力分成3'和4'处的力。对于整体守恒差值,界面上的总力和总热率平衡,但是局部分布可能不平衡。对于本文的研究对象,结构均匀各向同性,适用于整体守恒差值方法。
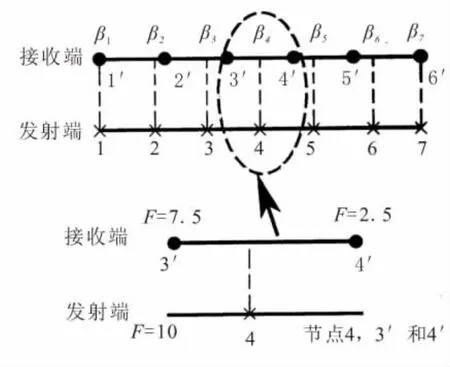
图1 整体守恒插值方法示意图Fig.1 Overall conservative interpolation method
为了传递载荷跨越不同的网格界面,一个网格的节点必须映射到另一个网格中一个单元的局部坐标上。也就是说,本项目中一次完整的数据交换传递对每个面对面界面进行2次映射,即流场耦合面上的节点必须映射到固体耦合面的单元上,以便把热通量传递给固体结构,而固体耦合面上的节点必须映射到流体耦合面的单元上,以便把热通量传递给流体区域。
常见的映射方法有整体和桶式搜索方法。本文数值模型的整体结构比较规则,为了保证映射的足够正确,选用计算量较大的整体搜索算法,即当前节点沿另一个网格中所有现有的单元循环,以寻找一个能够映射的单元。
2 结构模型及计算模型
2.1 结构模型
本文根据文献[14]设计了一种热密封结构,如图2所示。该结构由结构部件、密封部件共同组成。图3为密封结构各组成部分的具体尺寸(图中尺寸单位为“mm”)。各部件的材料参数如表1所示。
2.2 计算模型及网格划分
对结构各部件进行前处理并划分结构化网格模型,如图4所示,整体耦合计算区域网格划分结果如图5所示(其中外围流场位于结构区域上方)。外围流场区域的长度为结构区域长度(图2中左-右方向)的50倍,外围流场区域的宽度为结构区域宽度(图2中上-下方向)的20倍。最终整体计算区域网格数量为168 617(其中结构部件网格数为68 125,内部空腔流场网格数为11 982)。
2.3 计算参数及边界条件
对于内部空腔的流动传热,为保证以后复杂模型的通用性,本文同样基于可压缩N-S方程求解。
初始计算参数为:来流压强p0=3.5 kPa,温度T0=800 K,来流速度V0=1 800 m/s,来流方向为图11中左方流向右方;内外流场初始均温为T1=280 K,内外流场初始压强均为p1=450 Pa,内外流场速度均为V1=0;固体部分统一均温为280 K,与流体域相同。
然后根据给定初始条件,计算得到其他必要的流动参数。

其中,B与气体种类有关的常数,此处设为理想空气取110.4 K。
这样可得到:
来流运动粘度 μ0=2.998×10-5Pa·s;
初始流场运动粘度 μ1=1.447×10-5Pa·s。

图2 热密封结构模型Fig.2 Heat-sealing structure model
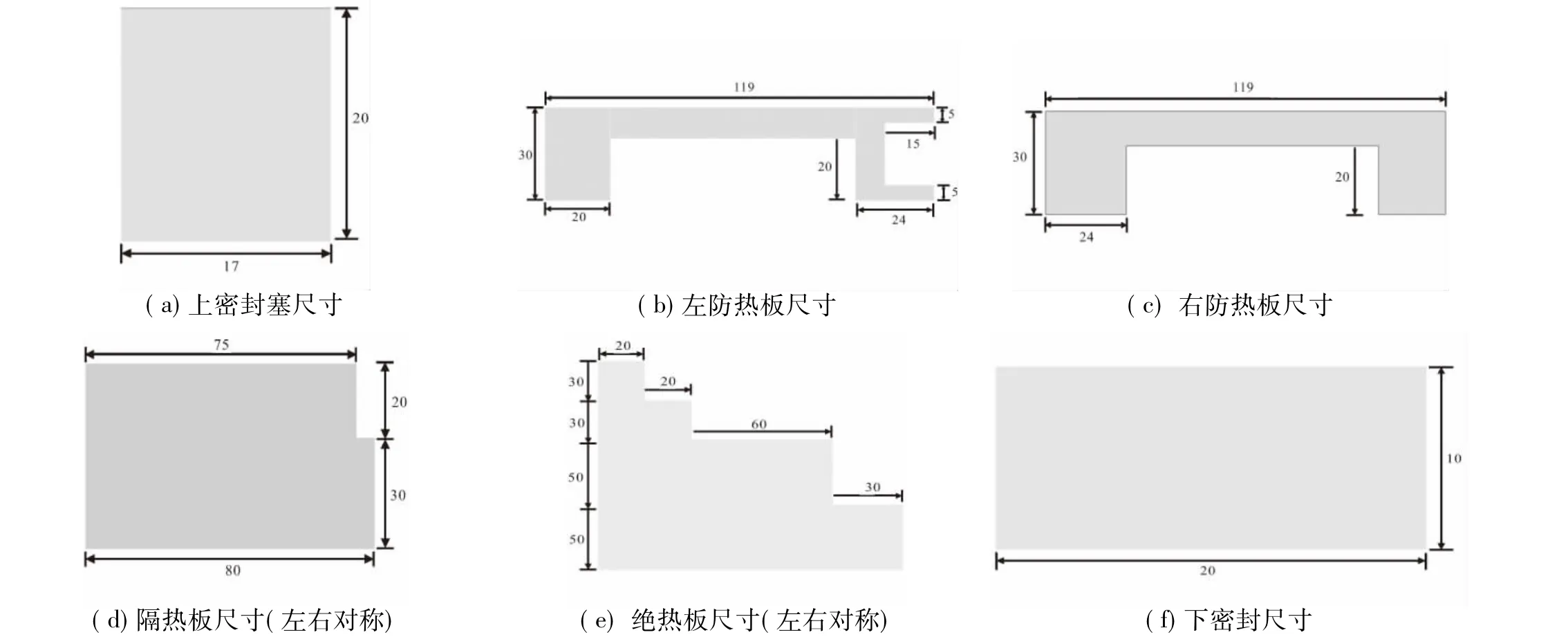
图3 密封结构各组成部分的具体尺寸Fig.3 Size of each component for sealing structure
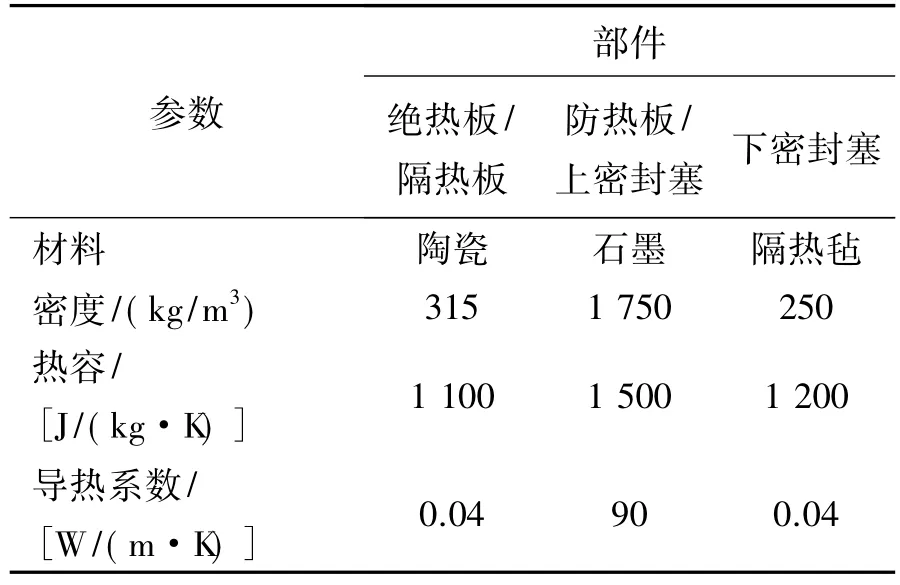
表1 材料参数Table 1 Material parameters
此外流场区域出口边界设为超声速出口,上下边界设为绝热壁面,耦合壁面均设不考虑粗糙度的影响。时间步根据上密封塞上部边缘的空隙最小长度与来流速度的比值取为10-7s,计算时间长度为200 s,每0.1 s保存一步计算结果。
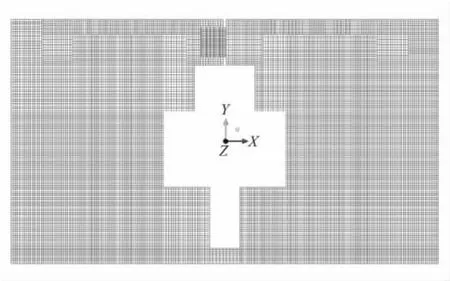
图4 结构部分网格Fig.4 Mesh generation of the structure parts

图5 整体计算区域网格Fig.5 Meshes of the overall computational region
3 计算结果及分析
本文首先进行了不加入上密封塞的瞬态耦合分析。0~200 s间内部空腔的温度场计算结果如图6所示,其中每幅图中的左图表示有密封塞的情况,右图表示无上密封塞的情况。
上密封塞外围的高超声速流动、密封塞内部空腔的低速流动以及结构各部件的热传导在每一时间步均进行流-固耦合传热作用,随着时间的推移,流体与固体区域的温度场分布在不断变化。本文算例中不考虑固体结构各部件的变形作用,只考虑其耦合传热特性。
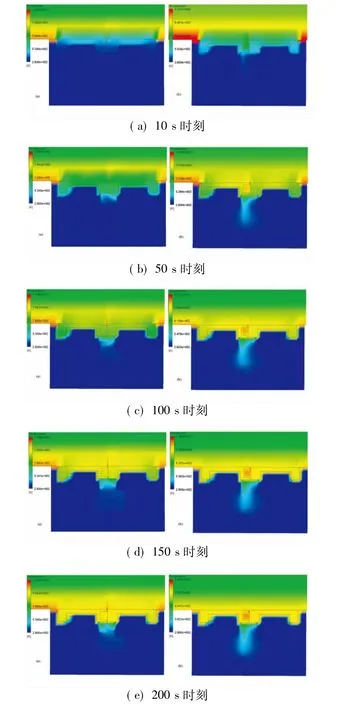
图6 温度场计算结果Fig.6 Temperature distribution
可以发现,当使用上密封塞时,内部空腔的最高温度显著降低,同时受外围高温气流影响的区域也相对较小,并且随着时间的推移,温度增长的速度明显变慢,这说明上密封塞及防热板吸收了大量外围气流带来的热量,保护了内部空腔。表2给出了0~200 s中不同时刻的上密封塞的最高温度值及有无上密封塞情况下内部空腔不同时刻的最高温度值。
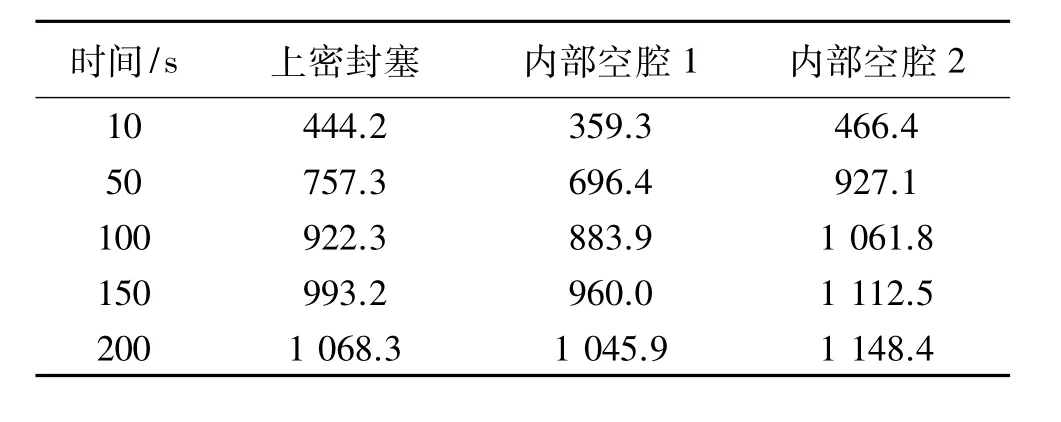
表2 不同时间上密封塞和内部空腔的最高温度值Table 2 The highest values of the temperature of upper sealing plug and the inside cavity at different times K
综合图7及表2可发现,上密封塞由于采用了石墨材料,最终温度也比较高,内部空腔在靠近密封塞的地方温度较高,其他则大部分处于低温状态。
表3给出了不同时刻有无上密封塞2种情况下内部空腔的压强值。可以发现,当使用上密封塞时,内部空腔由于温度的升高,压强升高很快,而不使用上密封塞时,压强则变化并不明显。
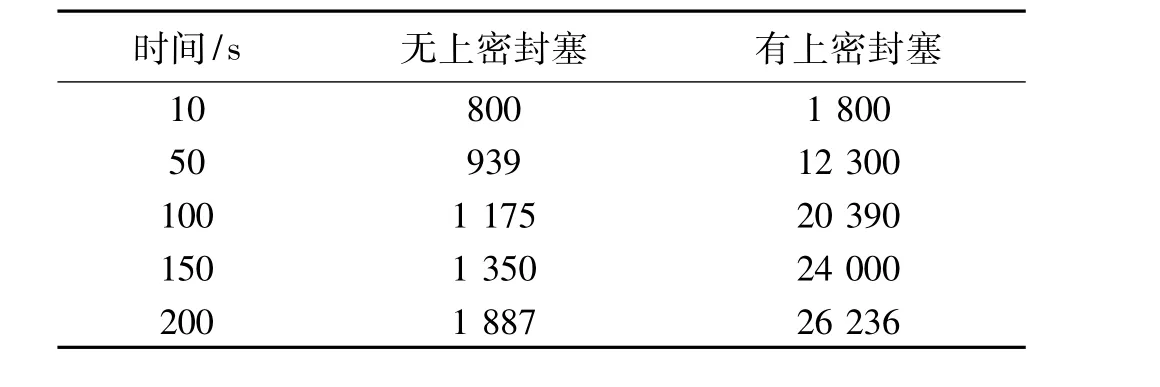
表3 不同时间内部空腔的最大压强值Table 3 Maximal pressure values of the inside cavity at different time Pa
图7为0~200 s中不同时刻内部空腔的速度场分布,可发现,随着内部空腔的温度、压强的逐渐升高,其速度场分布也随之产生变化;不同时刻的最大流速不断增大,并且均在内部空腔中靠近上密封塞的位置出现。
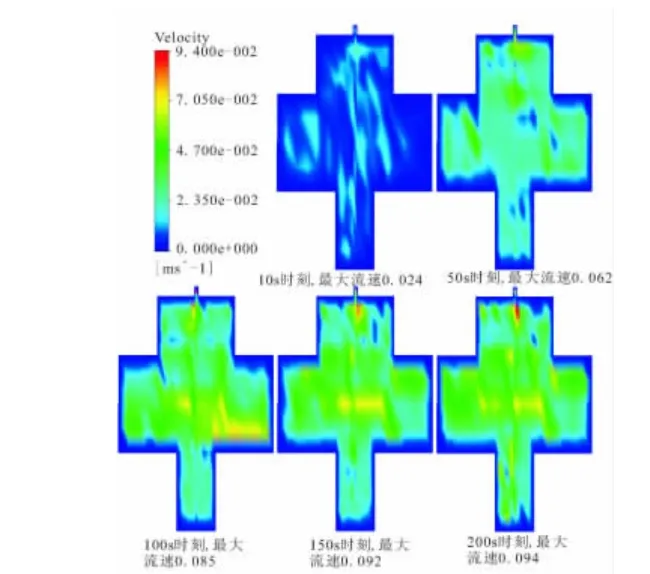
图7 不同时刻内部空腔的速度场分布Fig.7 Velocity distribution of the inside cavity at different time
值得注意的是,当采用上密封塞进行数值计算时,由于外围高超声速流动带来的热气流被上密封塞阻挡不能及时进入内部空腔,同时上密封塞上部与左右防热板之间构成了一个带有钝头尖角的间隙,因此产生了明显的流动分离现象,这在不采用上密封塞的数值计算过程中也存在,但不如前者明显。这说明在实际工程中,应尽量避免类似外端钝头间隙的存在,以防止局部温度过高。
4 结论
(1)利用改进型Van Driest变换方法进行航天器外围高超声速流动环境预测,而后基于高斯-赛德尔分块迭代耦合方法提出了航天器热密封结构的瞬态多物理场耦合分析方法。该方法综合考虑航天器舱体外围高超声速流动、密封部件及舱体结构传热以及密封结构内部空腔的流动传热,可有效地进行高温热密封部件的数值分析。
(2)计算了有无上密封塞2种情况下的热密封结构温度场和压强场分布。计算结果表明,密封塞的使用显著降低了结构内部空腔的最高温度,阻碍了高温对内部结构的损害。同时瞬时温度场和压强场的计算符合实际物理现象,本文数值方法的使用得到了合理的计算结果。
(3)目前常见的CFD方法或者基于密度求解器来进行高超声速流动数值分析,或者基于压力求解器来进行低速流动数值分析,能同时进行两种不同类型流动数值分析的方法还很少见。本文方法不仅可同时考虑不同类型流动的数值分析,还可同时兼顾固体结构的数值分析,因此本文方法可广泛应用于航天飞行器飞行过程中的热密封结构瞬态多物理场耦合分析。下一步的研究可基于本文的数值方法考虑复杂环境下多种不同密封材料变形、传热传质等特性对密封部件密封性能的影响,为航天器上各类高温热密封部件的设计提供有效的数值分析工具。
[1]吴国庭.载人飞船舷窗防热与密封结构的设计与试验[J].航天器工程,2007,16(3):99-105.
[2]Finkbeiner J R,Dunlap Jr P H,Steinetz B M.Review of seal designs on the Apollo spacecraft[J].Journal of Spacecraft and Rockets,2008,45(5):900-910.
[3]Foote J O,Foote J.Titan IV solid rocket motor upgrade program at Alliant Techsystems Inc[R].AIAA 97-2991.
[4]唐贵明.控制翼缝隙流传热实验研究[J].空气动力学学报,1989(1):88-93.
[5]Jeffrey J D,Patrick H D,Bruce M S,et al.An evaluation of high temperature airframe seals for advanced hypersonic vehicles[R].AIAA 2007-5743.
[6]李理科,王之栎,宋飞,王伟,陈聪慧.刷式密封温度场数值研究[J].航空动力学报,2010,25(5):1018-1024.
[7]张彪,齐宏,阮立明.二维多孔热密封材料的有效导热系数模拟 [J].物理学报,2012,33(7):1229-1232.
[8]Matthies H G,Steindorf J.Partitioned but strongly coupled iteration schemes for nonlinear fluid-structure interaction [J].Computers & Structures,2002,80(27-30):1991-1999.
[9]Bai Y G,Yang K,Sun D K,et al.Numerical aerodynamic analysis of bluff bodies at a high Reynolds number with three dimensional CFD modeling [J].SCIENCE CHINA Physics,Mechanics & Astronomy,2013,56(2):277-289.
[10]Bai Y G,Zhang Y G,Liu Y F,et al.Numerical analysis of a heater with conjugate heat transfer[J].Advanced Materials Research,2013,629:711-715.
[11]Cebeci T.Analysis of turbulent flows [M].Elsevier,London,2004.
[12]Zhang Y S,Bi W T,Hussain F,et al.Mach-number-invariant mean-velocity profile of compressible turbulent boundary layers [J].Physical Review Letters,2012,109(5):054502.
[13]Kader B A.Temperature and concentration profiles in fully turbulent boundary layers[J].International Journal of Heat and Mass Transfer,1981,24(9):1541-1544.
[14]GE Advanced Sealing Technologies[R].General Electric Brochure,Atlanta,GA,2000.
(编辑:吕耀辉)
Research on numerical method of heat-sealing structure for spacecraft hull based on multi-physics coupling
BAI Yu-guang1,2,XIA Guang-qing1,2,SUN De-chuan1,2,GAO Xiao-wei1,2
(1.State Key Laboratory of Structural Analysis for Industrial Equipment,Dalian University of Technology,Dalian 116023,China;2.School of Aeronautics and Astronautics,Dalian University of Technology,Dalian 116023,China)
A transient multi-physics coupling analysis method which can present the overall consideration of the peripheral hypersonic flow outside the structure,heat and mass transfer of the heat-sealing part and hull structure and flow and heat transfer in the interior cavity of the high temperature heat-sealing structure for the spacecraft was proposed in this paper.The developed Van Driest transformation was employed to predict the hypersonic flow environment.The integrated coupling analysis method was presented with a Gauss-Seidel block-iterative coupling method.A composite structure including several parts with different material was adopted.A time trace of 0-200 s for the transient heat transfer process was considered with two cases:with the sealing plug and without the sealing plug.Results show that the usage of the sealing structure can decrease the highest temperature of the interior cavity significantly and the consideration of the transient changes can present the changing process of the heat transfer and temperature distribution among the structure parts and the interior cavity.The numerical method proposed in this paper can be widely applied for the heat transfer analysis of the heat-sealing structures of the spacecraft and it can provide an effective numerical analysis tool for the design of the heat-sealing structures of the spacecraft such as the rocket.
multi-physics coupling;heat-sealing structure;transient heat transfer;Van Driest transformation
V421
A
1006-2793(2014)06-0756-07
10.7673/j.issn.1006-2793.2014.06.004
2014-05-09;
2014-08-12。
中央高校基本科研业务费(No.DUT14RC(3)044);中国博士后科学基金(No:2013M541230)。
白瑜光(1981—),男,博士,研究方向为飞行器热防护。E-mail:baiyg@dlut.edu.cn
夏广庆(1979—),男,副教授,研究方向为航空宇航推进理论与工程。E-mail:gq.xia@dlut.edu.cn

