基于扩张状态观测器的小型固体火箭控制系统设计与验证①
李 彤,张士峰,杨华波,张银辉
(国防科技大学航天科学与工程学院,长沙 410073)
基于扩张状态观测器的小型固体火箭控制系统设计与验证①
李 彤,张士峰,杨华波,张银辉
(国防科技大学航天科学与工程学院,长沙 410073)
以自研小型固体火箭为对象,基于扩张状态观测器,对三通道姿态控制器进行了设计及验证。建立了以攻角、侧滑角和滚转角为控制目标的积分链状态空间模型;结合扩张状态观测器,应用极点配置法对三通道姿态控制器进行了鲁棒设计;通过数值仿真和半实物仿真,结合拉偏分析,对控制器设计进行校核,证明了设计的有效性和鲁棒性;通过飞行试验验证了控制器性能,跟踪结果符合仿真分析,基本无延时、无静差,证明了该方法的可行性和工程应用价值。
小型固体火箭;姿态控制器;扩张状态观测器;半实物仿真;飞行试验
0 引言
固体火箭控制系统设计是一个传统难题。经典的线性设计方法[1]以其简易性和工程可行性已应用至今,通过对飞行包线特征点控制器设计,并进行增益调度而实现全局性能,但控制器参数人工整定需耗费一定时间和人力资源。随着固体火箭机动性不断提高,非线性对火箭动力学特性影响愈加明显,传统线性方法已难以满足要求,非线性设计方法应运而生,如动态逆、滑模变结构、鲁棒 H∞设计等[2-4],在仿真中得到了令人满意的性能。然而,由于模型和环境参数以及扰动的不确定性,非线性设计方法往往难以保证鲁棒性要求,因此在实际工程应用中受到了较强制约。
由韩京清[5]最早提出的扩张状态观测器技术很好地解决了这一问题,通过扩张状态观测器对内外扰动和不确定性实时估计和补偿,保证系统鲁棒性。同时,结合线性设计方法,可大大简化控制器设计复杂度,有效利用了经典方法和现代控制理论的优势。Talole S E及其团队[6-7]基于扩张观状态测器分别对战术导弹滚转通道和俯仰通道进行了控制器设计,在考虑干扰和不确定因素下对比了该方法与传统PID控制、最优控制、反馈线性化控制、滑模控制以及预测控制等控制设计方法,验证了该方法的可行性和优越性。然而,该方法目前的应用多基于非线性模型反馈线性化,这在一定程度上增加了实现难度,且该方法尚停留在理论研究和仿真阶段,在飞行器工程应用中并无先例。
目前,国内外很多大学积极进行小型火箭的研究,如美国普渡大学的SHLV[8]、北京航空航天大学的“北航2号”[9]等。“天航”系列小型固体火箭由国防科技大学自主研发,由动力、气动、结构、回收、GNC等系统组成,研制过程包含火箭设计、制造、测试和飞行试验的完整生命周期,具有研制耗时短、成本低、功能多样化等特点。
本文将以“天航二号”小型固体火箭为对象,基于扩张状态观测器,对三通道姿态控制器进行设计,在给出工程实现途径的基础上,进一步对控制器性能进行验证。首先建立三通道数学模型,其次结合扩张状态观测器对三通道姿态控制器进行鲁棒设计,而后通过数值仿真和半实物仿真校验控制器性能,最后通过飞行试验验证控制器设计效果。
1 数学模型
扩张状态观测器的应用需建立积分链型数学模型[5],而以往的研究[7]多基于非线性模型的反馈线性化,由于非线性模型的获取及反馈线性化的计算过程较为复杂,如将高阶气动数组进行非线性拟合、计算系统状态高阶微分量等,这都将极大增加方法的实现难度。为此,本文结合传统设计方法,在获取简化三通道传递函数基础上,建立积分链形式的状态空间模型,可极大简化设计复杂度。
1.1 姿态运动模型及线性化
“天航二号”小火箭采用“×·-”布局轴对称气动外形,外形如图1所示。

图1“天航二号”小型固体火箭Fig.1 Physical map of“SkyFly II”small solid rocket
小火箭飞行高度不超过1 km,飞行速度为亚声速,因此根据文献[10],为简化模型以实现线性化,可作如下假设:
(1)只考虑弹体姿态运动方程,忽略质心运动和长周期运动参数如速度、重力等对姿态运动的影响。
(2)侧向运动姿态参数、侧向操纵机构偏转角以及纵向姿态参数(俯仰角和速度倾角除外)为小量,略去它们之间的乘积以及这些参数与其他小量的乘积,将它们的三角函数关系式用近似式表示。
(3)忽略洗流延迟及马格努斯力矩作用,只考虑执行机构的偏转所产生力矩对弹体姿态的影响,忽略所产生气动力对质心运动的影响。
(4)忽略偏航和滚转的交叉耦合作用。
由此,采用小扰动线性化和固化系数法,可得三通道解耦的小扰动线性化姿态运动方程。
纵向姿态运动方程:

式中 α、β、γ分别为攻角、侧滑角和滚转角;ωx1、ωy1、ωz1为弹体角速度在弹体系内三轴上的分量;δx、δy、δz分别为俯仰、偏航和滚转通道的舵偏指令;ɑij、bij为气动相关动力学系数。
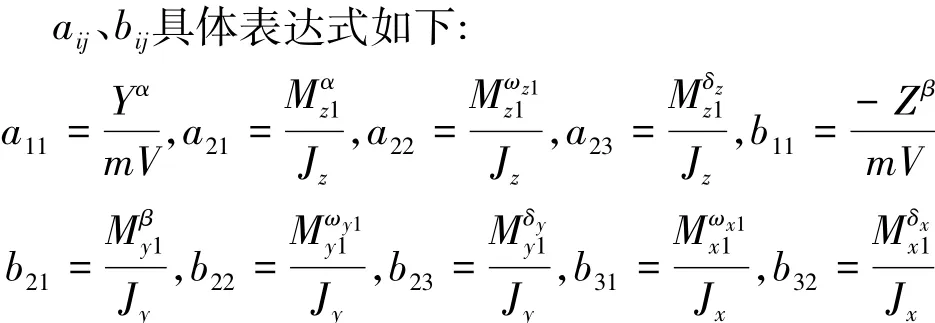
式中 Y、Z分别为升力和侧力;Jx、Jy、Jz分别为三轴转动惯量;Mx1、My1、Mz1为气动力矩在弹体系三轴上的分量;m为质量;V为速度;上标代表对相应变量的偏导数。
1.2 状态空间的建立
“天航二号”小火箭姿态控制系统采用三通道控制策略。俯仰通道采用攻角跟踪控制,偏航通道和滚转通道分别采用侧滑角和滚转角稳定控制。由式(1)和式(2),通过拉氏变换,可得三通道传递函数如下。
俯仰通道:
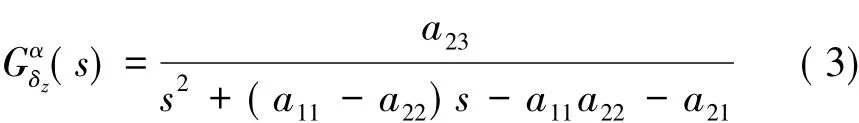
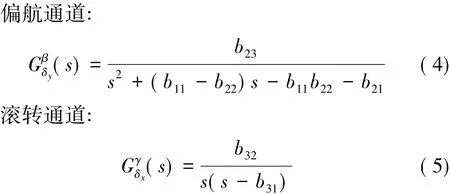
可见,在不考虑舵机系统的情况下,三通道传递函数均为二阶,为方便扩张状态观测器设计,可将其转化为积分链形式的状态空间实现。

由此,三通道建立了积分链型状态空间模型。下文将针上述系统,进行控制器设计。
2 姿态控制器的设计
2.1 扩张状态观测器
扩张状态观测器是在状态观测器的基础上,将影响系统的外部扰动、模型不确定性、非线性等作用因素视为一个总的等效扰动,并将其扩展成一个新的状态变量,利用观测器对等效扰动进行估计,从而便于实现扰动的实时补偿。
对于一个n阶单输入单输出积分链系统如下:

式中 fo(·)为已知的系统动力学关于状态变量的线性主干部分;Δf(·)为未知的非线性和扰动部分;bo为输入增益的最优有效估值;Δb为输入增益的不确定性。
定义总的扰动为d·Δf+Δbu,并将其扩张为系统一个新状态变量xn+1,则系统状态方程可写为

2.2 控制器综合设计
基于简化的小火箭三通道二阶积分链系统模型,控制器的设计可采用统一方法,具有一致性。稳定控制可视为参考输入为0的跟踪控制,在小扰动方程基础上,将跟踪偏差作为状态量,并将由此产生的模型偏差视为扰动的一部分。针对如下状态空间模型:
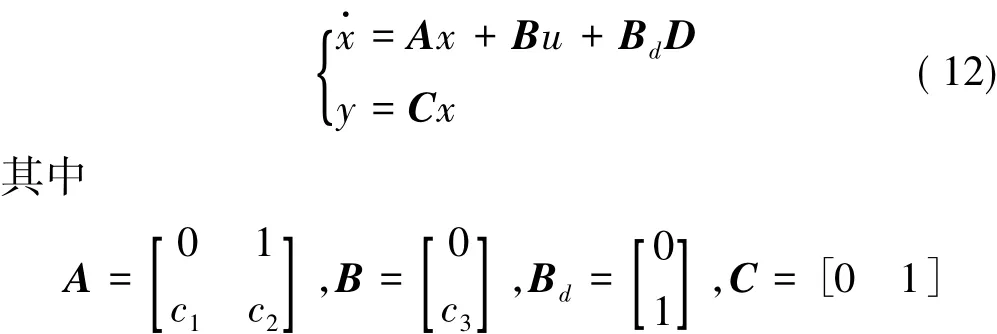
式中 Bd为扰动输入矩阵;d为总的等效扰动。
控制器可应用极点配置法进行设计,以保证控制器的收敛性,则状态反馈为

由此,同样应用极点配置可设计线性扩张状态观测器如下:
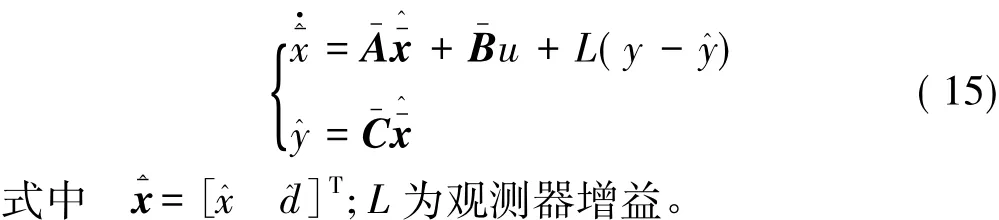
通常情况下,系统(12)并不能保证是全状态可用的。因此,扩张状态观测器不仅为状态反馈提供了状态观测量,同时也对扰动进行了实时估计,可通过控制输入在线补偿。故综合控制律可设计如下:
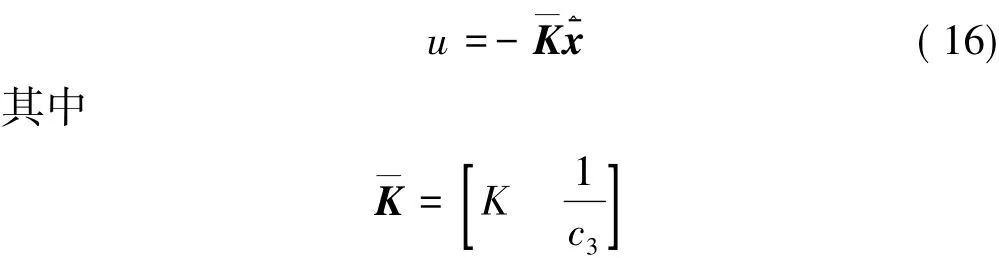
控制器结构图如图2所示。其中,r(t)为参考指令信号,λ(t)为相应的受控姿态角信号。可见,控制器设计同时保证了性能和鲁棒性,且仅需要单一测量观测量。
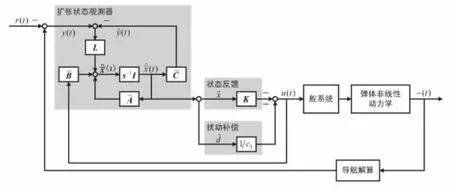
图2 控制器设计结构图Fig.2 Configuration of the designed controller
2.3 稳定性分析
针对上述控制器设计,可定义扩张状态观测器观测误差向量为


3 数值仿真
3.1 仿真模型及弹道设计
仿真模型基于MATLAB/SIMULINK搭建,根据文献[10]中发射系下质心动力学和运动学方程和弹体系下姿态运动方程及转换关系,建立了小火箭六自由度仿真模型。

可见,舵机带宽为10 Hz。根据舵机性能指标,其死区为 0.1°,转速限制为 200°/s,最大偏转角度为 20°。
气动模型采用基于气动计算和工程估算的以攻角、侧滑角、马赫数和4个舵偏角为变量的7维数据插值表。
推力模型采用基于单室双推力固体发动机地面实验数据插值,由于小火箭飞行高度较低,可保证其推力变化与实验数据基本一致。
敏感装置采用高精度MEMS惯组和GPS组合导航,姿态和位置信息由导航系统实时解算。
弹道设计攻角指令采用先下压后上拉方案,并按如下正弦平滑处理:
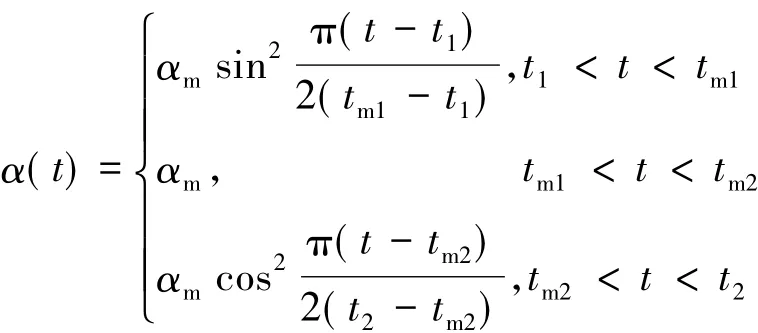
式中 αm为攻角最大绝对值;t1、t2为信号起始和结束时间;tm1、tm2为信号达到最大绝对值的时间。
这里分别取 αm为-5°和 5°,t1为 3 s和 13 s,t2为11 s和 21 s,tm1为 6 s和 16 s,tm2为 8 s和 18 s。
图3给出了设计弹道的主要参数。可见,小火箭发射角为75°,最大高度约为600 m,射程约为1 000 m,最大马赫数约为 0.35。
三通道姿态控制器结构参考图2设计,根据舵机性能和控制要求,结合工程经验,为保证攻角跟踪精度,令攻角控制器系统极点均配置在1 Hz(2π rad/s)。为克服偏航和滚转通道间耦合作用影响,可设计滚转角控制系统动态特性快于侧滑角控制系统,因此侧滑角控制极点均配置在0.5 Hz,滚转角控制均配置在0.75 Hz。同时,为保证稳定性要求,将相应扩张状态观测器极点配置在8倍于闭环系统极点,即8、4、6 Hz。攻角、侧滑角和滚转角观测量可由导航解算实时获取。
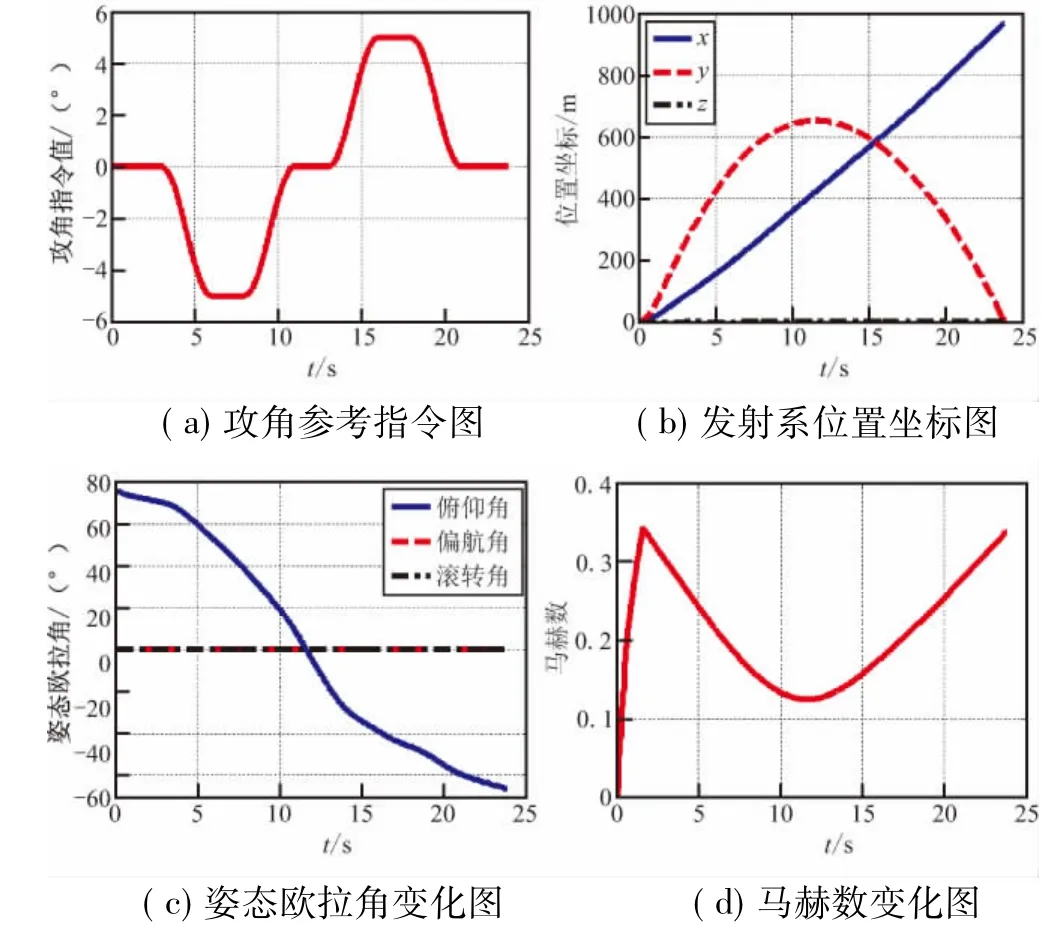
图3 设计弹道主要参数图Fig.3 Variation of the main parameters in designed trajectory
3.2 控制器参数选择
三通道控制器设计性能要求满足调整时间不大于1 s,超调量小于5%,稳态误差小于1%。根据设计弹道,可选取1.66 s发动机关机时刻各参数值作为控制器设计模型参数。表1给出了控制器设计所需的动力学系数。
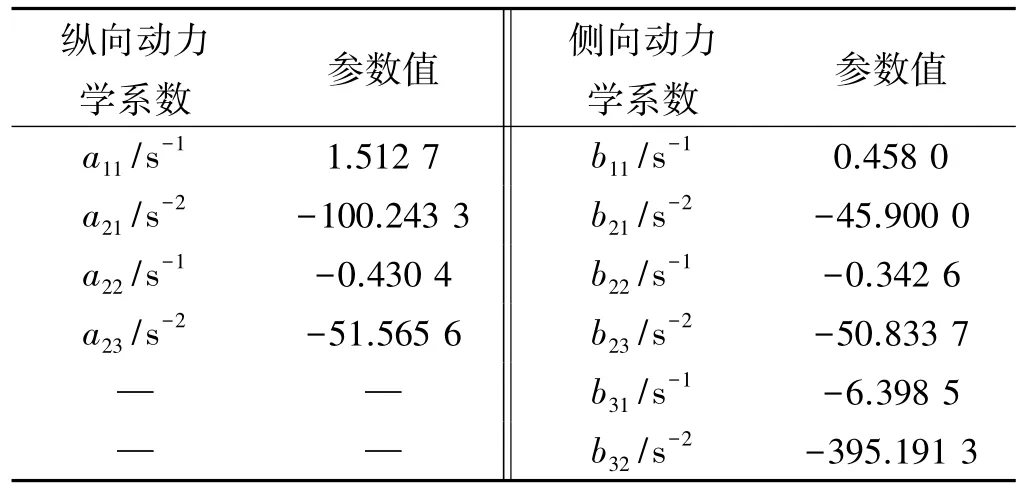
表1 1.66 s时刻相关动力学系数参数值Table 1 Values of the dynamic parameters at 1.66 s
3.3 数值仿真结果
数值仿真步长设为1 ms,积分算法设为4阶龙格库塔法。额定状态无扰条件下仿真结果如图4所示。等效扰动实际值可根据系统(12)按下式求取:
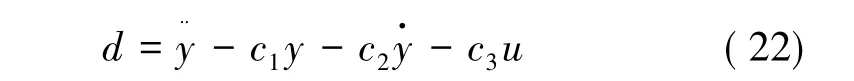
由图4可看出,在无扰条件下,三通道姿态跟踪误差几乎为0,控制器控制精度高,响应迅速无超调,扩张状态观测器对扰动进行了较为精确的估计,成功补偿了模型非线性和未建模动态特性(如舵机环节等)的影响,控制指令和舵偏角均在10°以内,仿真结果令人满意,验证了控制器的可行性。
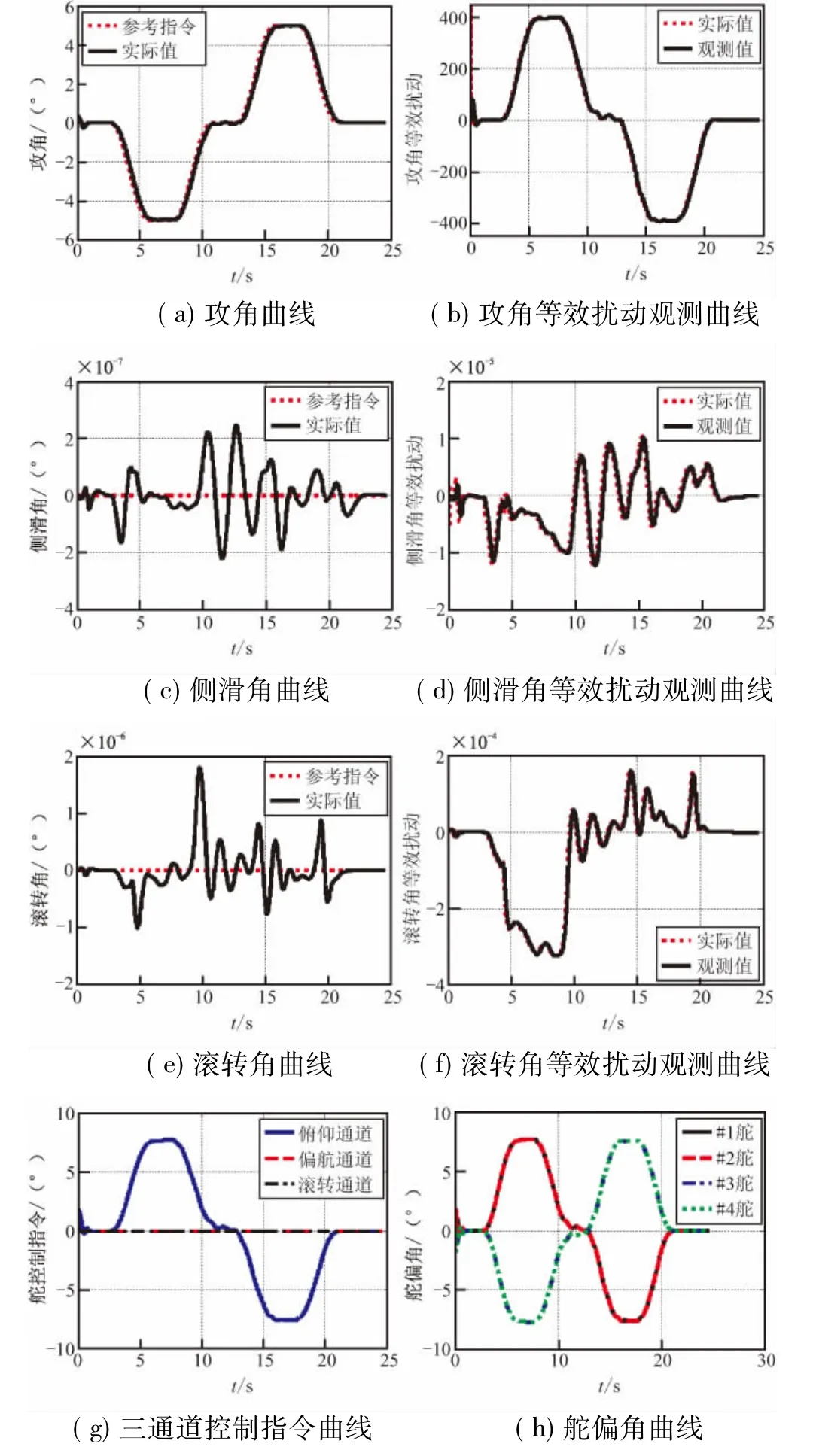
图4 无扰条件下数值仿真结果Fig.4 Result of the numerical simulation without uncertainty
图5给出了一组极限拉偏条件下数值仿真结果,考虑气动力+20%,气动力矩-20%,密度-10%,三轴转动惯量+10%,质量+10%;舵机阻尼和自然频率-20%的偏差;翼安装偏差引起俯仰力矩系数+0.01偏差;尾舵安装偏差引起滚转力矩系数附加+0.02偏差,初始发射角+3°偏差,初始滚转角速度+5°/s偏差;GPS单点定位噪声-0.5~0.5 m,加表噪声均值为 0,零偏稳定性 0.002 g;陀螺仪噪声均值为 0,零偏稳定性 0.005°/s,水平风10 m/s与射向135°夹角。由图5可知,在拉偏条件下,控制器控制效果较好,抑制了扰动和模型偏差以及噪声影响,具有较强鲁棒性,满足基本要求。攻角跟踪仍较为精确,滚转角控制克服了尾舵安装偏差影响,控制效果无静差。侧滑角和滚转角受耦合作用影响,出现了较小振荡,但总体结果仍令人满意,控制指令满足舵机性能要求,控制器设计满足要求,进一步验证了控制器有效性。
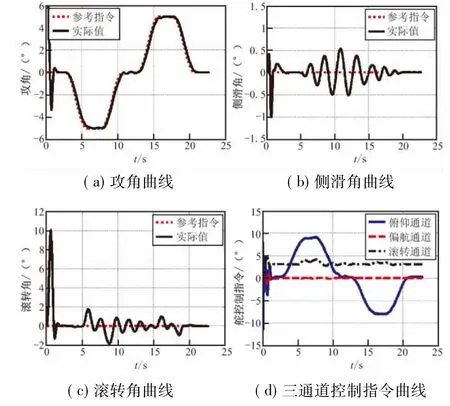
图5 拉偏条件下数值仿真结果图Fig.5 Result of the numerical simulation with uncertainties considered
4 半实物仿真
小火箭半实物仿真平台在文献[12]基础上设计搭建,如图6所示。弹载计算机采用TMS320F28335型DSP控制器,平台基于 dSPACE实时仿真机的RS4201S串口板卡,其中3个通道采用RS422方式与转台控制串口相连,实现对转台的控制;一个通道采用RS232串口方式与DSP相连,传送DSP接收的舵机控制反馈信号。另外,MEMS惯组和DSP安装在转台上,DSP采用RS232串口方式与舵机控制器相连,以实现对舵机的控制以及对舵机反馈信号的接收;MEMS惯组与DSP相连,DSP通过A/D模块进行采集,实时测量转台角度。
半实物仿真SIMULINK模型设置与数值仿真基本一致,除去舵机与陀螺仪仿真模型,DSP控制周期为5 mm。图7给出了一组极限拉偏条件下半实物仿真结果,考虑气动力-20%,气动力矩+20%,密度+10%,三轴转动惯量-10%,质量-10%;翼安装偏差引起俯仰力矩系数+0.01偏差;尾舵安装偏差引起滚转力矩系数附加+0.02偏差,初始发射角-3°偏差,初始滚转角速度-5°/s偏差;GPS 单点定位噪声-0.5~0.5 m,加表噪声均值为0,零偏稳定性0.002 g,水平风10 m/s与射向45°夹角。
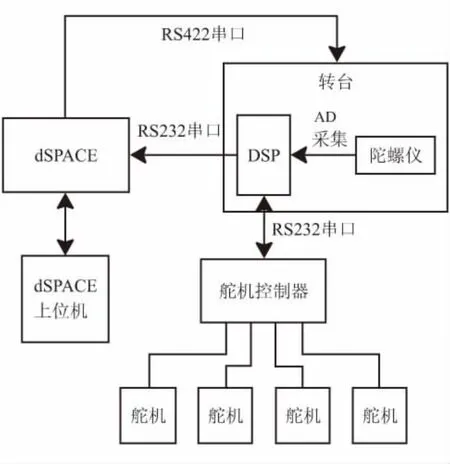
图6 小火箭半实物仿真平台结构示意图Fig.6 Structure diagram of hardware-in-the-loop simulation platform of small rocket
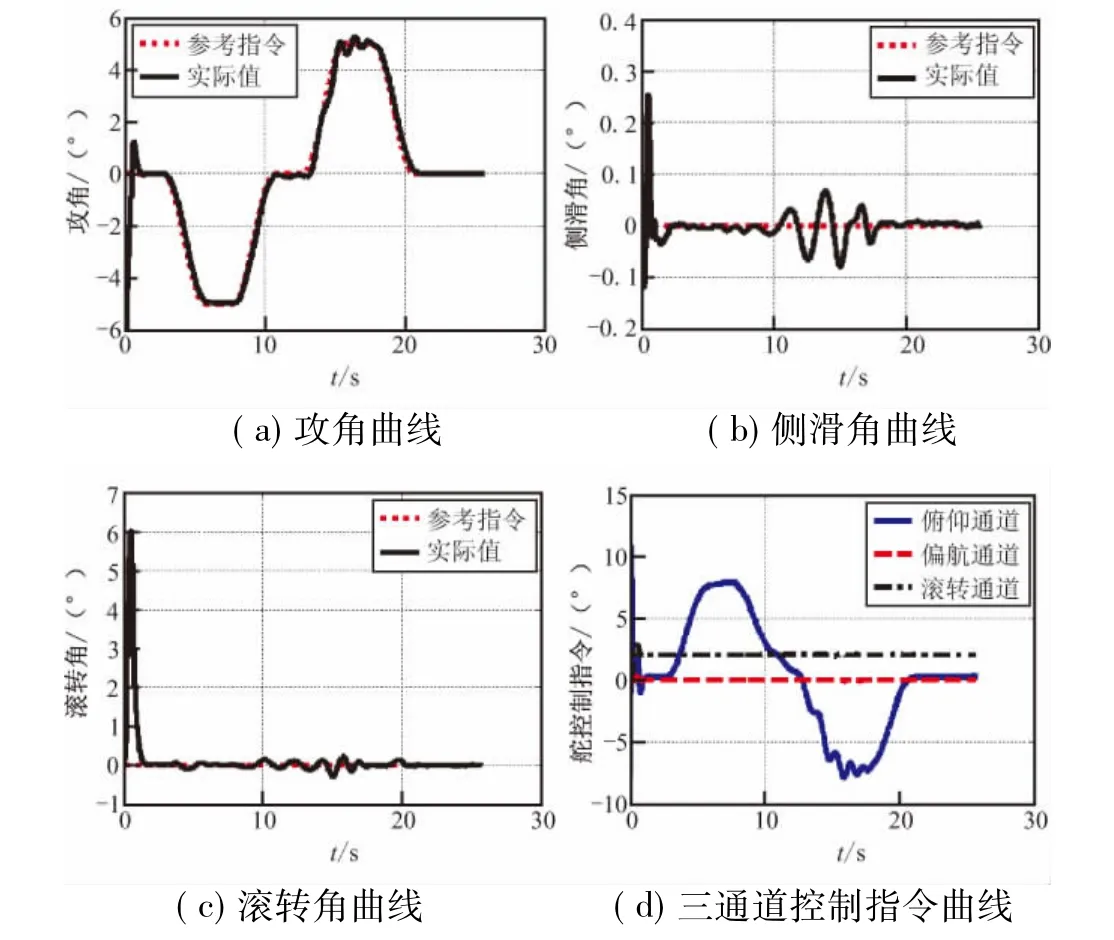
图7 拉偏条件下半实物仿真结果图Fig.7 Result of the hardware-in-the-loop simulation with uncertainties considered
如图7所示,拉偏条件下控制系统半实物仿真结果基本满足要求。攻角跟踪在上拉过程中出现了一定抖动,但整体跟踪效果良好,侧滑角和滚转角均能快速克服扰动,在较小范围内保持稳定。控制指令满足舵机性能要求,由于舵机反馈信号存在噪声,对控制器性能有一定影响。整体而言,姿态控制系统性能满足要求,具有较好鲁棒性。
5 飞行试验
在仿真验证基础上,成功进行了“天航二号”飞行试验。小火箭经现场组装测试后,应用发射架进行发射,在22 s时实施程序开伞并回收,成功对相关各项技术进行了验证。飞行试验数据由弹载电台发送,遥测电台实时接收。图8给出了飞行试验数据经分析处理后的三通道姿态控制结果。
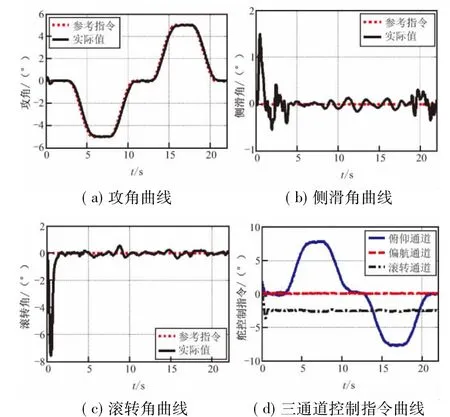
图8 飞行试验姿态控制结果Fig.8 Performance of the attitude controllerin the flight-test
根据图8可知,飞行试验得到了令人满意的结果,与数值仿真和半实物仿真基本一致,验证了仿真分析的有效性。攻角基本无延时无差跟踪,由图8(b)中侧滑角曲线可知,侧向存在一定初始扰动,由图8(c)中滚转角曲线可知,尾舵存在与拉偏分析中相反的安装误差。飞行试验充分验证了控制器性能,控制器设计满足要求,实现了预定的控制效果,具有工程可行性。
6 结论
(1)仿真与飞行试验结果表明,所设计控制器在无扰、拉偏和实际飞行中均能达到令人满意的效果,跟踪无静差、无延时、无超调,对各种扰动具有较强的鲁棒性。该方法建立在传递函数基础上,并应用线性设计方法,充分结合了传统设计方法和现代控制理论;三通道设计统一一致,且控制器本身仅需要单一观测量,对模型和扰动信息依赖较小,单点控制器设计即可满足全局控制跟踪性能,极大简化了控制器设计的复杂度和应用限制条件。
(2)本文通过小型固体火箭三通道姿态控制器设计、仿真和飞行试验的完整周期,验证了本文设计方法的可行性和鲁棒性,提供了工程实现途径和工程应用先例,进一步说明该方法在工程领域具有较高应用价值,也为相关控制器设计提供了借鉴,具有广泛的应用前景与一定实践意义。
[1]Horton M P.Autopilots for tactical missiles:an overview[J].Proceedings of the Institution of Mechanical Engineers Part IJournal of Systems and Control Engineering,1995,209(2):127-139.
[2]Schumacher C and Khargonekar P P.Stability analysis of a missile control system with a dynamic inversion controller[J].Journal of Guidance Control and Dynamics,1998,21(3):508-515.
[3]Salamci M U,Oslash M K,et al.Sliding mode control with optimal sliding surfaces for missile autopilot design[J].Journal of Guidance Control and Dynamics,2000,23(4):719-727.
[4]Buschek H.Full envelope missile autopilot design using gain scheduled robust control[J].Journal of Guidance Control and Dynamics,1999,22(1):115-122.
[5]韩京清.自抗扰控制技术——估计补偿不确定因素的控制技术[M].北京:国防工业出版社,2009.
[6]Talole S E and Godbole A A,et al.Robust roll autopilot design for tactical missiles[J].Journal of Guidance Control and Dynamics,2011,34(1):107-117.
[7]Godbole A A,Libin T R,Talole S E.Extended state observerbased robust pitch autopilot design for tactical missiles[J].Proceedings of the Institution of Mechanical Engineers Part G-Journal of Aerospace Engineering,2012,226(12):1482-1501.
[8]John T.Progress in technology demonstration for a small hybrid launch vehicle[C]//AIAA 5th Responsive Space Conference,Los Angeles,2007:1-19.
[9]李秀卿.北航学生自制火箭“北航2号”成功升天[J].中国科技奖励,2008,112(14):79-79.
[10]钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2008.
[11]Li S H,Yang J,et al.Generalized extended state observer based control for systems with mismatched uncertainties[J].IEEE Transactions on Industrial Electronics,2012,59(12):4792-4802.
[12]张银辉,程见童,等.小型固体火箭控制系统设计与半实物仿真验证[J].固体火箭技术,2012,35(1):29-33.
(编辑:吕耀辉)
Extended state observer based small solid rocket control system design and validation
LI Tong,ZHANG Shi-feng,YANG Hua-bo,ZHANG Yin-hui
(College of Aerospace Science and Technology,National University of Defense Technology,Changsha 410073,China)
The design and validation for the three-channel attitude controller of a self-developed small solid rocket based on the extended state observer approach were presented.The integral-chain state space model was established for the control design of the angle of attack,angle of sideslip and roll angle;Combined with the extended state observer,the pole placement was applied to the robust design of the three-channel attitude controller;Through numerical and hardware-in-the-loop simulation with uncertainties considered,the effectiveness and robustness of the controller were illustrated and verified.The performance of the controller was validated by flight-test with results of nearly no time delay or state error conforming to the simulation,which illustrates the feasibility and the engineering application value.
small solid rocket;attitude controller;extended state observer;hardware-in-the-loop simulation;flight-test
V448
A
1006-2793(2014)06-0749-07
10.7673/j.issn.1006-2793.2014.06.003
2014-07-29;
2014-09-25。
国防科学技术大学研究生创新资助项目(S140104)。
李彤(1989—),男,硕士生,研究方向为飞行器动力学与控制。E-mail:li.tong.1202@gmail.com

