基于LQR的弹道跟踪制导律设计①

张大元，雷虎民，吴 玲，邵 雷，王 君

(1.空军工程大学防空反导学院，西安 710051;2.辽宁大学，沈阳 110036)

基于LQR的弹道跟踪制导律设计①

张大元1，雷虎民1，吴 玲2，邵 雷1，王 君1

(1.空军工程大学防空反导学院，西安 710051;2.辽宁大学，沈阳 110036)

针对防空导弹弹道跟踪问题，基于线性二次型调节器(LQR)理论设计了2种弹道跟踪制导律。首先，以时间为自变量，对导弹质点运动模型线性化，得到第一种线性化模型;接着，为提高模型精度和允许扰动范围，以导弹X坐标为自变量对导弹质点运动模型线性化，得到第二种线性化模型;然后，针对2种线性化模型，利用LQR理论分别设计跟踪制导律，并给出制导指令计算公式和制导流程;最后，在一定外界干扰作用下，将所设计2种跟踪制导律应用于导弹质点运动仿真，并从抑制随机风干扰、消除初始偏差等方面对2种制导律进行比较。结果表明，2种制导律都能实现弹道精确跟踪，且基于第2种线性化模型设计的跟踪制导律各项性能均优于第1种跟踪制导律，说明基于导弹X坐标线性化的模型精确度较高，适用于弹道跟踪制导律的设计。

弹道跟踪;制导律;最优控制;防空导弹

0 引言

飞行器轨迹优化可大大提高其飞行性能［1－5］。然而，大气中存在各种干扰，跟踪基准轨迹时也存在各种初始偏差，使得飞行器并不能理想跟踪优化轨迹。因此，需要设计轨迹跟踪制导律，保证飞行器按照理想弹道飞行［4］。轨迹优化和跟踪一直是飞行器领域研究的热点，许多非线性控制律被用于再入飞行器(RLV)和无人机的轨迹优化和跟踪，取得了较好的跟踪效果［6－11］;为提高远程防空导弹中制导段飞行性能，汤善同等研究了防空导弹的中制导弹道优化和弹道跟踪制导律问题［4］;文献［9］则采用几何原理研究了一种非线性方案弹道跟踪算法;Dukeman G A，Zhou W Y等先后将线性二次型调节器理论(LQR)用于再入飞行器的弹道跟踪中［10－11］，取得了较好效果，且易于实现。

本文利用LQR理论设计跟踪制导律，但采用不同的自变量对导弹质点运动模型线性化，得到2个不同的模型。基于这2个模型，分别设计了弹道跟踪制导律，并对其进行了仿真比较，得出了一些有益结论。

1 导弹质点运动模型

为简化问题讨论，考虑导弹在纵向平面内运动，其质点运动数学模型为［12］

其中，m、S为导弹质量和参考面积;V为速度;P为发动机推力;θ为弹道倾角;q为动压;g重力加速度;Cx、Cy为阻力系数和升力系数，其计算公式为

导弹气动系数［13］如图1所示。导弹质量和发动机特性如图2所示。

图1 导弹气动参数Fig.1 Dynamic coefficients

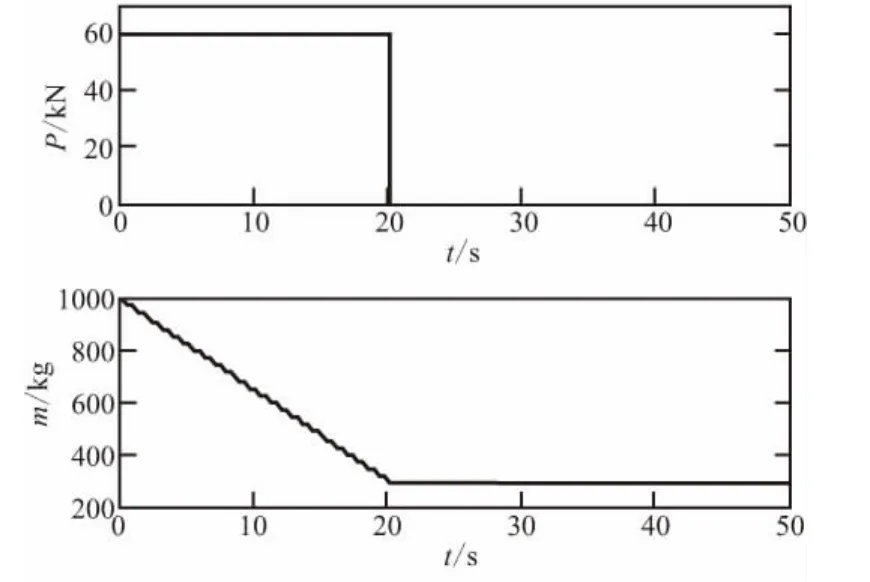
图2 导弹发动机推力特性和质量变化Fig.2 Curve of trust and mass

大气密度ρ和重力加速度g计算公式为

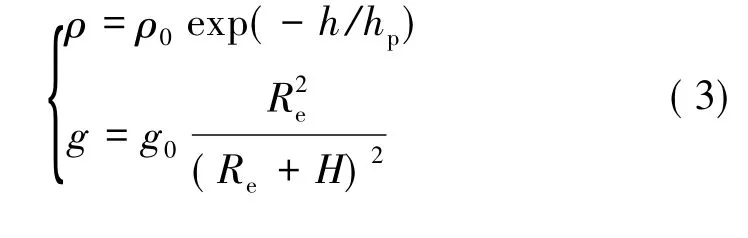
式中 ρ0=1.225 0 kg/m3为地面处空气密度;hp=7 254.3 m，g0=9.806 m/s2，Re=6 371 km，计算重力加速度时，略去地球椭球性及自转影响。

2 LQR弹道跟踪制导律设计

2.1 线性二次型调节器理论

根据线性二次型调节器理论，对式(4)线性系统:

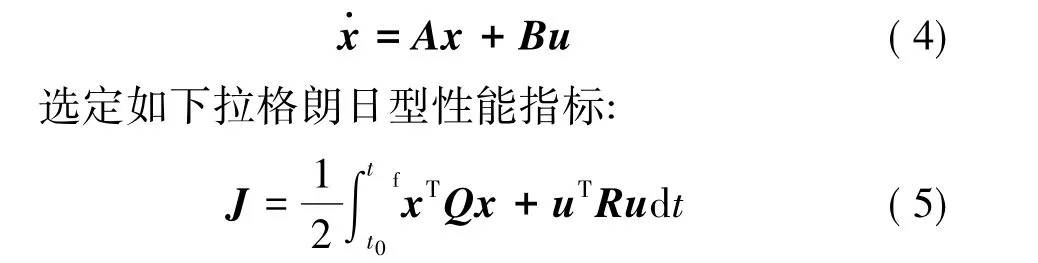
其中，Q、R为权重矩阵，且Q半正定，R正定。该指标物理意义为设计控制变量u，使用最少的控制能量，使得状态量x在整个控制过程中最小。根据LQR理论，存在最优控制变量u*=－Koptx，使得上述指标最小，且反馈系数Kopt为

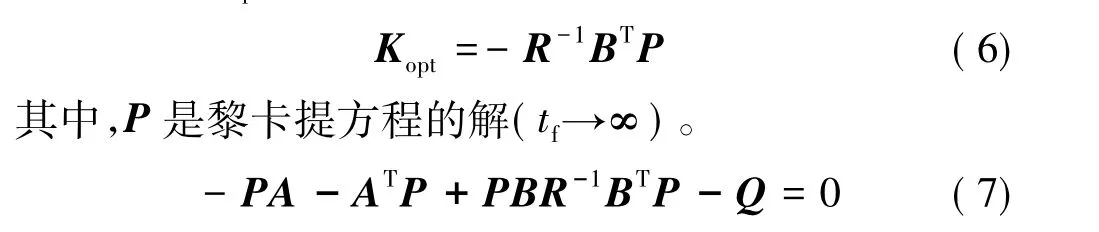
所谓弹道跟踪问题就是希望导弹实际飞行弹道与给定弹道参数(如位置、弹道倾角等)偏差最小，因此，可选定全部或部分弹道参数的偏差作为状态变量，建立线性化状态空间方程，选定式(5)所示的性能指标，使用LQR理论设计最优反馈增益Kopt，使得弹道偏差最小。显然，非线性模型(1)不能直接用于LQR理论设计弹道跟踪制导律。下面选择不同的自变量将导弹运动模型线性化，然后利用线性化的模型近似替代该质点模型，设计跟踪制导律。

2.2 线性化模型I

在小扰动假设条件下，以时间为自变量，在优化弹道附近对导弹质点运动模型(1)线性化，得含有气动力系数、动压和气动力系数导数项的线性化方程［12］:

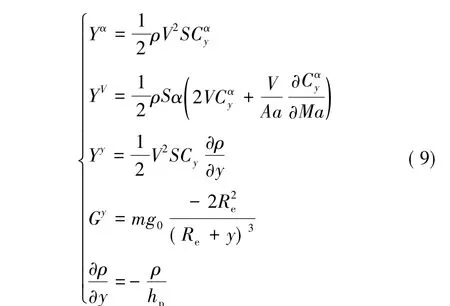
式中 Aɑ为声速;下标“0”代表导弹在标称优化弹道上的值。

在战术导弹设计阶段，一般首先进行速度特性设计，从而确定发动机参数;而在制导律设计中，仅设计纵向和侧向过载指令，弹体轴向不进行控制。因此，可假设导弹速度V和X坐标不可控，从而将速度方程和X方程从方程组中除去，限制导弹攻角绝对值小于20°，则有sin α≈α，得弹道坐标系下导弹纵向过载:

2.3 线性化模型II

在上面的线性化过程，以导弹运动时间为自变量，战术导弹飞行时间一般较短，在几十秒到一百秒的范围内，而导弹飞行距离则较大，可达几十公里至一百公里。因此，如果选择导弹运动X坐标作为自变量，使用固化系数法，认为导弹在与基准弹道的坐标X偏差较小时气动参数不变，可得到新的线性化模型。

由前面分析知，导弹速度几乎不可控，从而将速度方程从方程组中除去;选择X坐标作为独立变量，从而除去时间变量，得新的导弹运动方程:

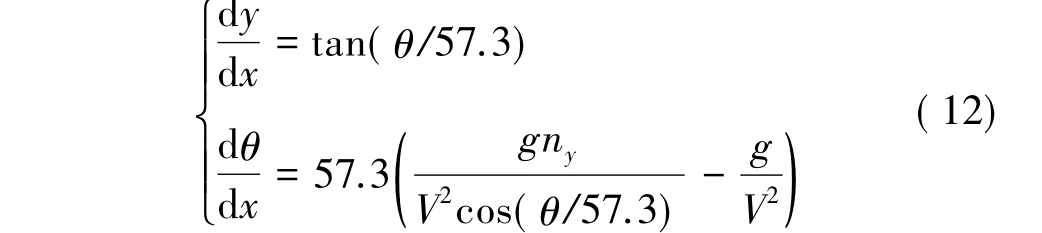
同理，取扰动系统的状态变量x=［Δy Δθ］T，取弹道纵向过载为控制量，即u=Δny，由式(9)可得新的扰动系统状态方程:

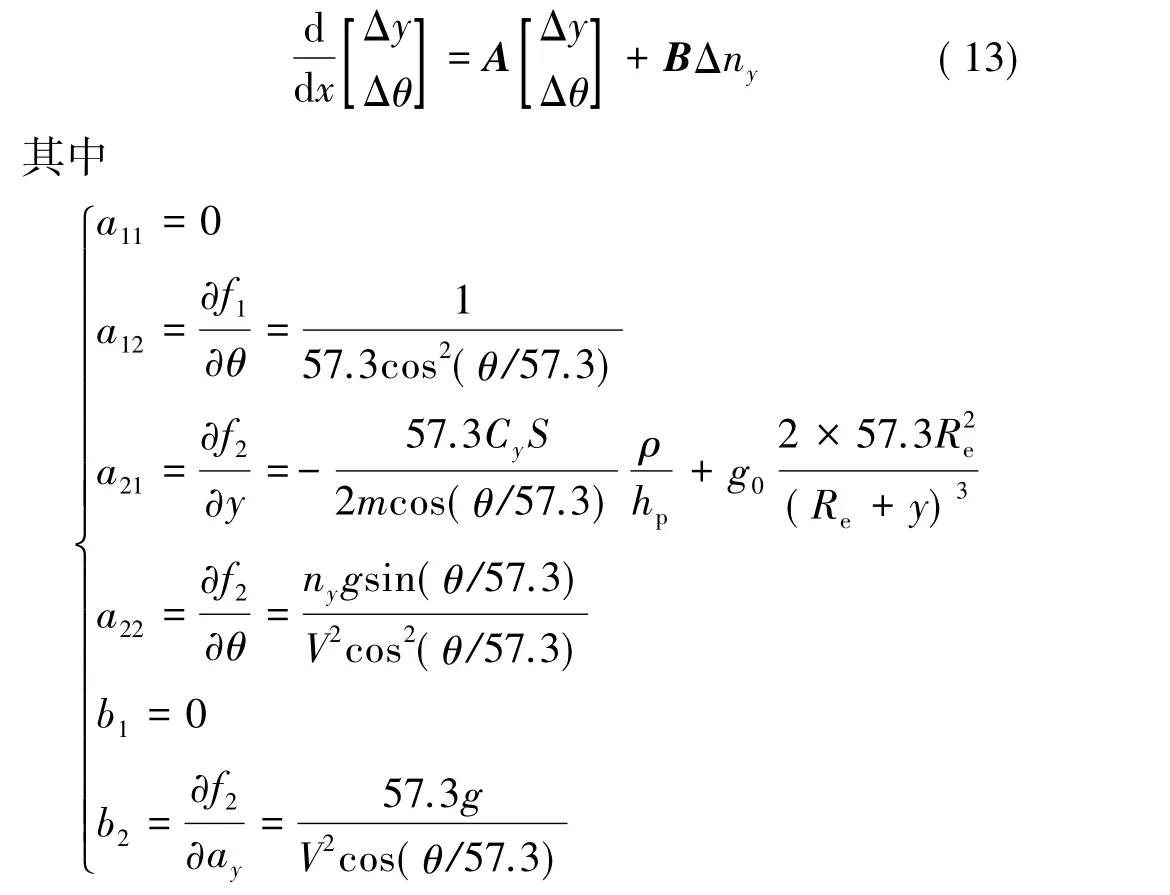
2.4 跟踪制导律及其工作流程

由2.1节跟踪问题的描述和LQR理论，使用上述2个线性化模型分别进行设计，可得反馈控制律:

使得导弹纵坐标偏差Δy和弹道倾角偏差Δθ最小，且需用过载u较小。设计步骤如下:

Step1:在优化弹道上按时间或X坐标等间隔取样，按照式(11)或式(13)获得导弹扰动运动的线性化模型参数;

Step2:按照式(5)、式(6)、式(7)选择权重指标，计算最优反馈增益矩阵Kopt;

Step3:将Kopt和标准优化弹道数据一并保存在弹载弹道数据库中，在导弹飞行过程中，按照时间或X坐标节点取用，按式(15)计算导弹运动状态偏差:

跟踪制导律闭环制导工作流程如图3所示。

由图3知，制导基本流程:首先，弹上惯导系统和弹载计算机测量、计算导弹运动状态，与弹上存储基准弹道相比较得出偏差量;然后，根据飞行时间或X坐标，从弹上计算机的基准弹道数据库中取出相应最优反馈增益，计算偏差控制量Δny和总控制量ny，控制导弹沿标称弹道飞行。

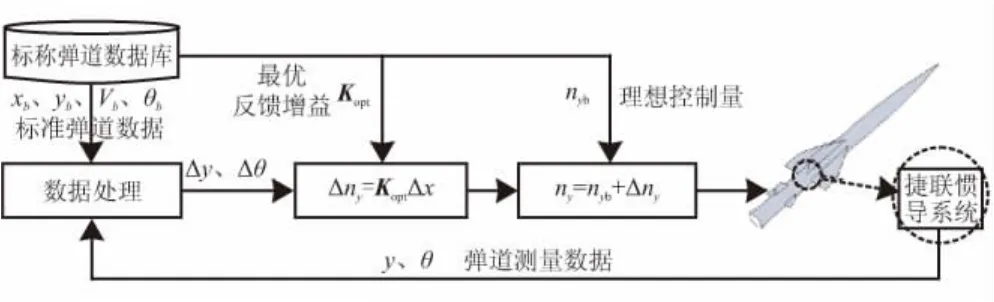
图3 LQR弹道跟踪制导律工作流程Fig.3 Flow chart of LQR guidance law

3 数字仿真

为验证所设计的弹道跟踪制导律有效性，将其应用于导弹质点运动仿真。首先，给出干扰添加方法。

3.1 随机风干扰数学模型

由文献［12］知，干扰力可等效为附加攻角，干扰攻角计算方法和步骤如下所示。

Step1:生成随机地面风根据风级定义，取μ=0，σ=4 m/s，则

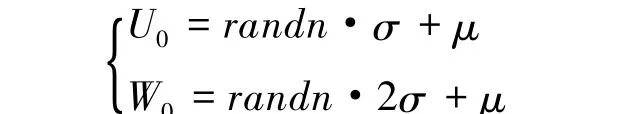
式中 U0为地面垂直风;W0为水平风;rɑndn为单位随机数;μ为均值;σ为均方差。

Step2:生成高空风

式中 U为高空垂直风;W为高空水平风;ρ0为地面处大气密度;ρ为高空大气密度。

Step3:计算干扰攻角分量

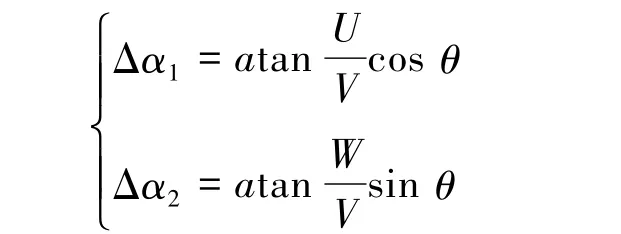
式中 Δα1为高空垂直风引起的干扰攻角;Δα2为高空水平风引起的干扰攻角;θ为导弹弹道倾角。

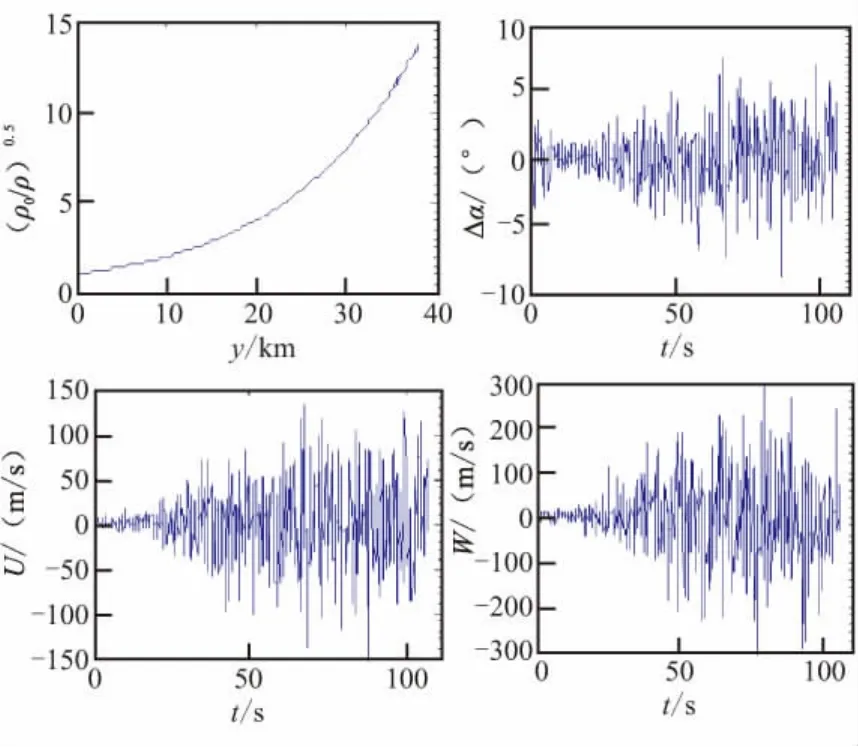
图4 等效干扰攻角Fig.4 Equivalent disturbance angle

3.2 仿真实验

仿真分别验证制导律抑制随机风干扰的能力、消除初始偏差的能力和对气动参数摄动的鲁棒性。仿真中认为，消除Δy、Δθ偏差和控制能量小的重要性一样。因此，制导律权重系数矩阵均为

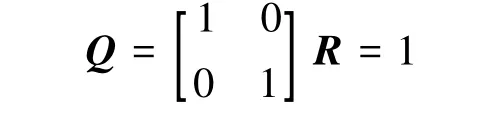
仿真中，导弹运动初始条件为X=0 m，Y=100 m，V=100 m/s，θ=90°。为简明起见，以下跟踪制导律1代表使用以时间为自变量得到的线性化模型所设计的跟踪制导律，跟踪制导律2代表使用以X坐标为自变量所得到的线性化模型设计的跟踪制导律。

仿真一:抑制随机风干扰的能力

令各种初始偏差为0，随机干扰见3.1节，分别使用2种LQR跟踪制导律跟踪某基准弹道，仿真结果见图5、图6及表1。

由图5、图6和表1的统计结果可知:

(1)基于2种线性化模型所设计的LQR弹道跟踪制导律，均能有效抑制随机风的干扰，保证导弹精确的跟踪理想弹道;但是，跟踪制导律2在ΔY上控制效果较好。

(2)ΔX、ΔV较大，这是由于设计制导律时没有考虑这两项的缘故，但与开环控制情形相比，ΔX减小约40%，ΔV仅有开环误差的60%。

(3)由图6控制量曲线可知，基于X线性化模型的制导律2控制量小于制导律1控制量，且较为平稳。

综上，可认为基于X变量线性化得到的模型所设计的跟踪制导律效果要好于基于时间线性化得到的制导律。这是因为在以时间为自变量的线性化过程中，直接将受控性较小的X状态方程忽略，引起一些不必要的误差。而以X为自变量的线性化过程，首先将该状态方程引入其他方程;然后，才是线性化过程。所以，引起控制效果不同。

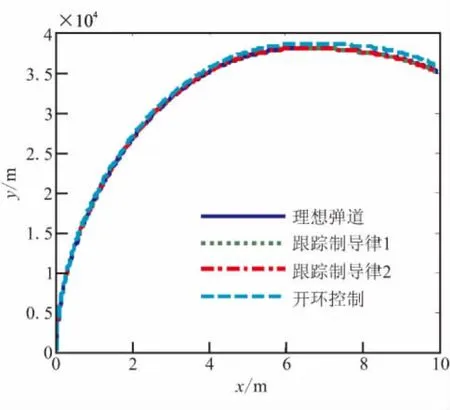
图5 弹道曲线Fig.5 Curve of trajectory

图6 误差量变化曲线Fig.6 Curve of errors

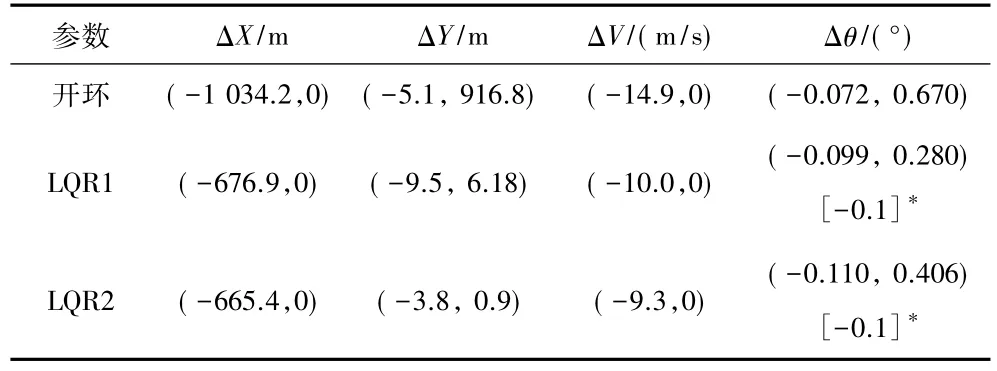
表1 仿真结果统计Table 1 Statistical data of simulation results

仿真二:消除初始误差的能力

为检验制导律消除单项初始偏差的性能，当其中一个偏差存在时，其余初始偏差为零，4次仿真中使用同一组随机风干扰(见3.1节)。4种仿真情形的初始偏差值见表2。由于数据较多，此处仅给出各误差量仿真结果，如图7、图8(图例ΔX代表该偏差项不为零，其他初始偏差为零时的仿真结果)所示。开环控制误差见表3。由图7、图8及表3的数据可知:

(1)X初始偏差引起开环控制ΔY急剧增大(达513 m);但对2种制导律影响较小(情形1数据)。因此，2种制导律对X初始偏差都不敏感。

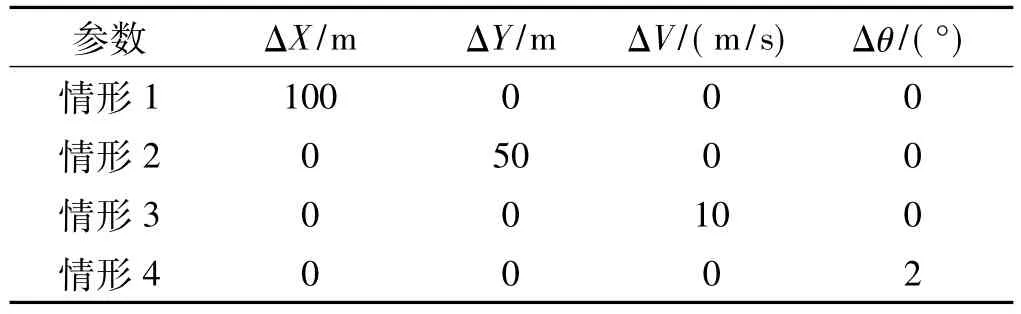
表2 仿真初始偏差Table 2 Initial simulation errors

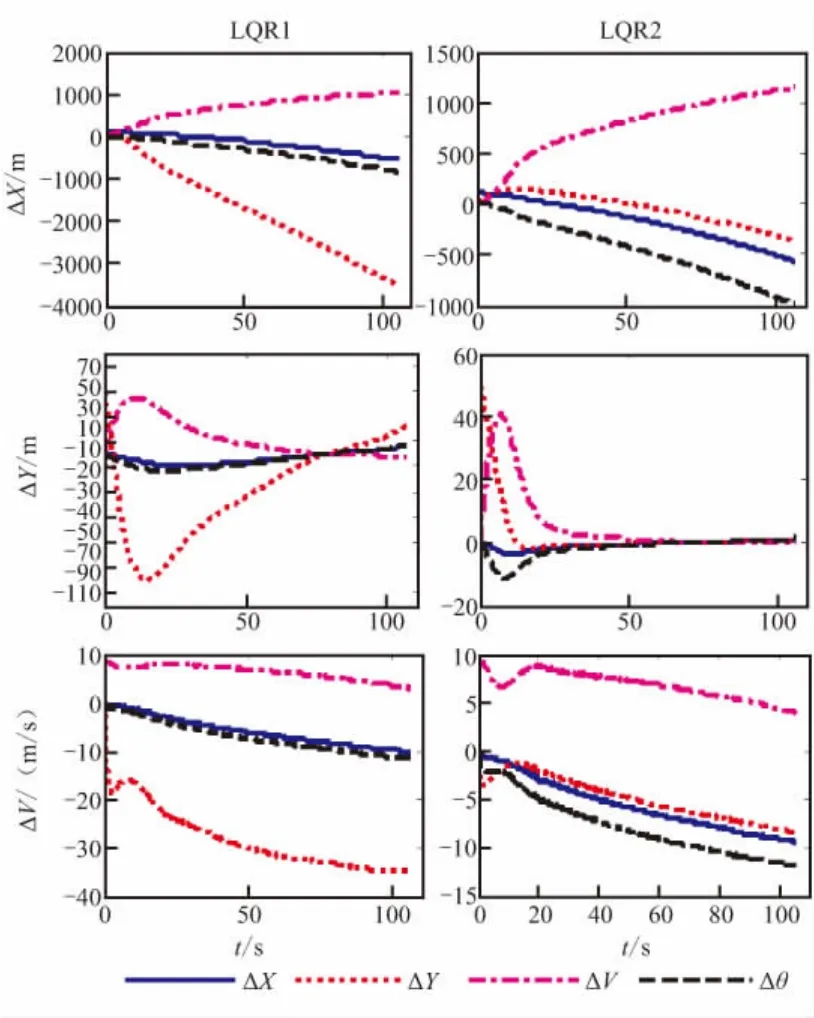
图7 X、Y和V误差变化曲线Fig.7 Curve of errors for X、Y and V

(2)由情形二数据可知，制导律1对Y的初始偏差十分敏感，其ΔX甚至大于开环值，而 ΔY误差高达－100，同时速度跟踪性能急剧下降，ΔV也大于开环，Δθ达－16°，原因可由图7分析得到:制导律1为消除初始Y偏差，使V急剧变化，引起θ急剧变化，使得弹道跟踪失稳，性能变差;相比之下，制导律2则能较快消除初始Y偏差，其他误差也较小，性能优异。

(3)情形三数据表明，速度初始偏差对2种制导律影响都较大，不管开环还是闭环制导，X坐标偏差均变大，这是由于制导律设计时没有对X偏差进行修正;速度初始偏差对开环ΔY影响较大，可达2 692 m;但2种制导律都能够消除速度初始偏差带来的影响，效果较好;与制导律1相比，制导律2对ΔY的调节速度快，性能优于制导律1。

(4)弹道倾角的初始偏差对开环弹道影响很大，ΔX、ΔY、ΔV、Δθ达到－5 119 m、6 061 m、－75 m/s、3.9°，而两种制导律均能较好消除初始弹道倾角偏差，其他偏差也较小。

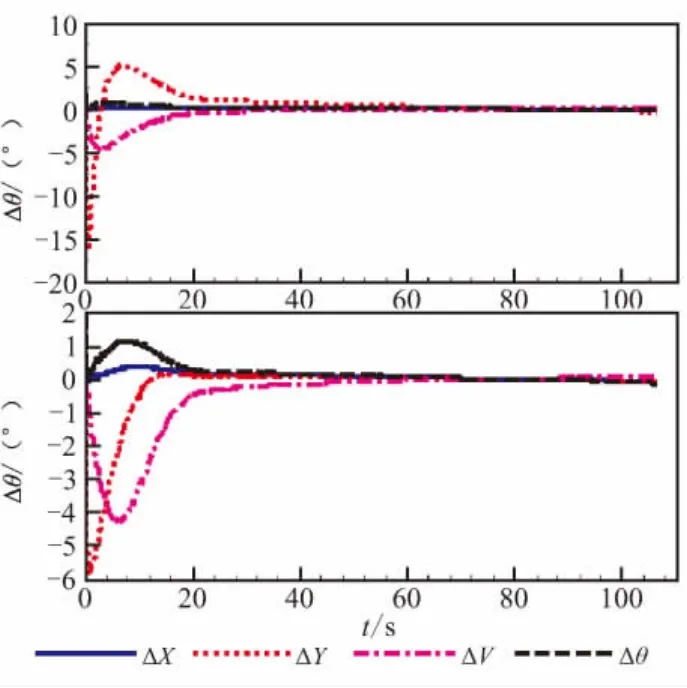
图8 弹道倾角误差变化曲线Fig.8 Curve of errors for Δθ

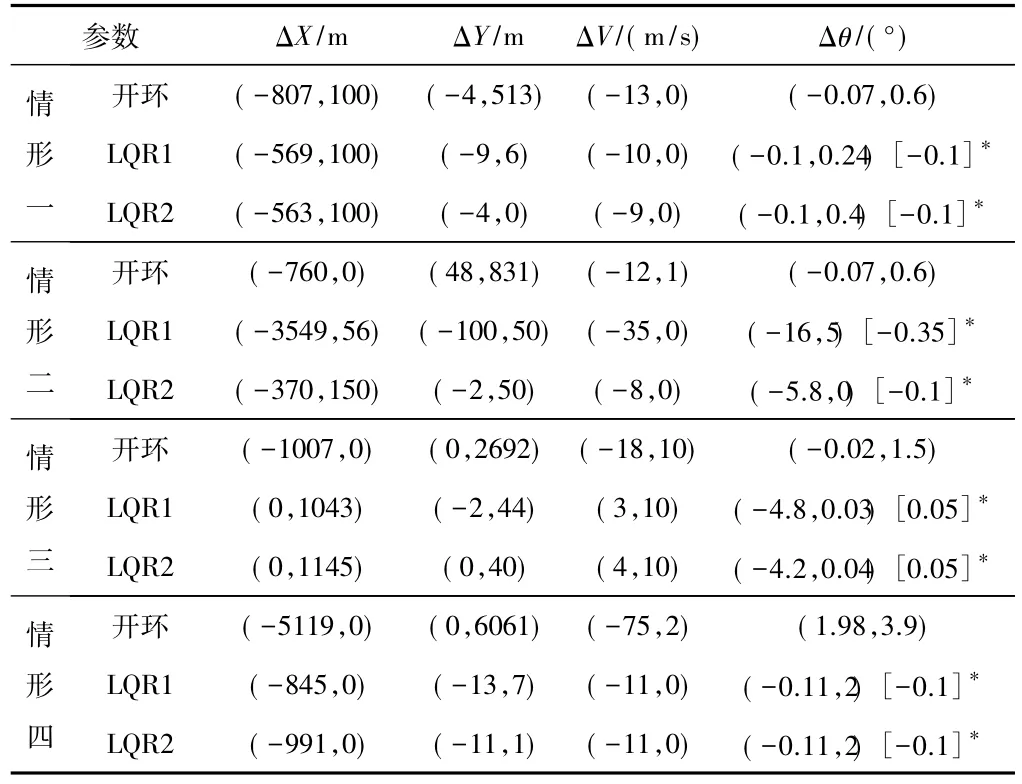
表3 误差范围统计Table 3 Range statistics of errors

4 结论

(1)为保证防空导弹沿优化弹道飞行，必须设计弹道跟踪制导律实施闭环制导，否则将造成较大误差。

(2)本文设计的2种制导律在小范围气动参数摄动的情况下，具有抑制随机风干扰的能力，在整个飞行过程中，弹道跟踪效果较好;2种制导律都具有消除初始偏差的能力，但制导律1对Y坐标初始偏差较为敏感;制导律2总体性能要优于制导律1，由于制导律设计方法一样，因此可认为基于X坐标的线性化模型效果好。

［1］李新国，王晨曦，王文虎.基于修正Newton法的固体火箭能量管理弹道设计［J］.固体火箭技术，2013，36(1):1-5.

［2］赵欣，闫循良，张金生，等.助推-滑翔导弹再入弹道快速优化［J］.固体火箭技术，2012，35(4):427-433.

［3］Levy M，Shima T，Gutman S.Linear quadratic integrated versus separated autopilot-guidance design［J］.Journal of Guidance，Control，and Dynamics，2013，36(6):1722-1730.

［4］汤善同，韩松臣.H∞控制在跟踪优化弹道自动驾驶仪设计中应用［J］.系统工程与电子技术，2002，24(9):62-65.

［5］谷学强，王楠，陈璟，等.基于鲁棒多目标优化方法的UCAV武器投放规划［J］.系统工程与电子技术，2013，35(4):753-760.

［6］Hakim Bouadi F，Mora-Camino.Aircraft trajectory tracking by nonlinear spatial inversion［C］//AIAA Guidance，Navigation，and Control Conference.Minneapolis，Minnesota，2012.

［7］Pu Z Q，Tan X M，Fan G L，et al.Design of entry trajectory tracking law for a hypersonic vehicle via inversion control［C］//Proc.of the 10th World Congress on Intelligent Control and Automation，2012:1092-1097.

［8］Yi Luo，Abraham K I，Kalmanje S Krishnakumar.Optimal lateral trajectory tracking using backstepping with a fully tuned growing RBF neural network［C］.Garden Grove，California USA，June 19-21，2012.

［9］Park S，Deyst J，How J P.A new nonlinear guidance logic for trajectory tracking［C］//AIAA Guidance，Navigation，and Control Conference and Exhibit.Rhode Island，2004.

［10］Greg A Dukeman.Profile-following entry guidance using linear quadratic regulator theory［C］//AIAA Guidance，Navigation，and Control Conference and Exhibit.Monterey，California，2002.

［11］Zhou W Y，Tan S J，Chen H B.A simple reentry trajectory generation and tracking scheme for common aero vehicle［C］//AIAA Guidance，Navigation，and Control Conference.Minneapolis，Minnesota，2012.

［12］李新国，方群.导弹飞行力学［M］.西安:西北工业大学出版社，2005.

［13］Muzumdar D V.Guidance laws for a short-range attack missile［D］.Austin:University of Texas.1995.

(编辑:薛永利)

A trajectory tracking guidance law based on LQR

ZHANG Da-yuan1，LEI Hu-min1，WU Ling2，SHAO Lei1，WANG Jun1
(1.Air and Missile Defense College，Air Force Engineering University，Xi’an 710051，China;2.Liaoning University，Shenyang 110036，China)

Two trajectory tracking guidance laws were designed based on the theory of linear quadratic regulator(LQR)，which can help to solve the problem of trajectory tracking for surface-to-air missile.Firstly，the variable of time was chosen to linearize the missile mass model to get the first linear model，and then，the coordinate variable of X axial was chosen to linearize the missile mass model to get the other linear model，which was more accurate;secondly，two trajectory tracking guidance laws were proposed with theory of linear quadratic regulator(LQR)and the two linear models given above，the flow chart of the guidance system was proposed too.Finally both of the laws were evaluated in simulations with uncertain disturbances，and were compared in two aspects as the ability to deal with disturbances and to remove the initial error.Results show that both laws can assure the trajectory tracking accurately，but the second one behaves better than the first one.

trajectory tracking;guidance law;optimal control;surface-to-air missile

V448.23

A

1006-2793(2014)06-0763-06

10.7673/j.issn.1006-2793.2014.06.005

2013-12-02;

2013-12-30。

张大元(1987—)，男，博士，研究方向为先进防御技术、导弹制导与控制技术以及武器系统仿真技术。E-mail:dayuanyjs@163.com