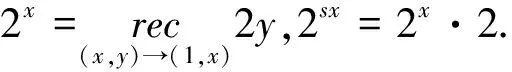关于连续统假设2ω0=ω1的证伪凡数皆可数2ω0=ω1的证明
陈自立
(海宁市建设局 浙江华恒建筑设计有限公司, 浙江 海宁 314400)
0 引言
1900年著名数学家希尔伯特在巴黎数学大会上的著名讲演《数学问题》中列举了二十三个未解决的问题中的第一个问题“2χo等于χ1吗?”(即2ωo=ω1吗?)康托猜想2χo=χ4是成立的,这就是连续统假设.即认为[0,1]不可数.
笔者首先破连续统假设的基石即其中的基本定理与基本方法.得到如本文所述的主要结论.
1 证伪“定理:ω1是一基数”
康托尔在集合论中提出基数概s念后,在无穷集合中建立了“定理:ω1是一基数”.这是无穷集合层次理论的基石之一.至今,未曾有人撼动它.《统一无穷理论》建立了计算机模型,认为无穷集合都是可数的.这在中国引起了极大的争论,不破不立.我们认为“定理:ω1是一基数”的证明不正确,现在简要叙述如下:
定义1.1[1]67令ω1={α|on(α)∧α≤ω}.
定义1.2[1]67令M={R|R是ω内一良序关系}.
定理1.1[1]67存在一类函数F,使得对于任一R,R∈M,都有F(R)∈ω1.
定理1.2[1]67对于任意的α∈ω1都有一R∈M使得F(R)=α.
定理1.3[1]68ω1是一集合.
定理1.4[1]68ω1是一基数.
首先证明ω1是一序数.由于ω1是序数的一集合,仅需明ω1=∪ω1;为此只需证明
1)ω1是传递的;2)ω1无最大元;(证略).

1.1 预备知识
定义1.3[1]44对于序数的任一集合S,和一个序数α∈S,使得α如果满足条件:
∀β[β∈S→[β∈α∨β=α]],
则我们称α是S的一个最大元.
定理1.5[1]44对于序数的任一集合S,如果α是S中的最大元,则有∪α=α.
定理1.6[1]44对于序数的任一集合S,如果S无最大元,且S≠θ,则序数∪S是一极限序数. ∪S的最小性是显然的.
定理1.7[2]285如果S是一序数集合,则S是∈连接的.
定义1.4[2]287令S为序数的任一给定集合,我们用符号Sups表示最小的序数α,使得∀β[β∈S→β∈α],并且称这一最小的序数α(Sups)为S的最小上界.
定理1.8[2]287对于任意给定的集合S,都有它的最小上界.
1) 当S中无最大元时Sups=∪S;

注2.5[1]45由定理2.3,及定理2.5对于任意的序数α,β:
1)α∈β↔α⊂+β且α⊂+β↔α<β;
2)α≤↔α⊆β.
因而有:∈↔⊂↔<;∈∨=↔⊆↔≤(≤). 这里⊂:=⊂+.
定义论:
(a) 定义之所以要有:是为了明确内涵与外延.
(b) 定义的基本原则与格式:
1)A是新引入的指词,即被定义单位,不得在定义谓词B(x)中出现.即A=B(x),in(A,B(x)).in(A,B(x).读A不在B(x))中出现.
2) 引进定义相当于引进一条公理;
3) 引进定义的存在性与唯一性;
4) 引进定义的不矛盾性.
例1n:n-1∪{n-1}={0,1,2,3,…,n-1};这里"n-1" 作为一个单位,用逗号隔开是不可分的整体.
n+1:n∪{n}={0,1,2,3,…,n},
“n+1”作为一个被定单位,不能出现在右边的定义式中(右边的单位用逗号隔开).
ω+ω:=Sup{ω+n|n∈ω}.[3]36
:=ω∪SO=ω∪{ω+n|n∈ω}={0,1,2,…,ω,ω+1,ω+2,…}[2]281,
其中SO={X|∃n[n∈ω∧X=ω+n].[2]279
ω+ω作为整体,是不能用反证法,出现在右边,证出ω+ω是一基数的,它仍然是一个序数.
定理1.9[2]301一可数集合或附加上一个有限集合或删去其中有限个元素,结果,仍是可数集合.(本文著者注:这可称为可数集合的吸收性)
定理1.10[2]302可数无穷多个可数集合的并集合仍是一可数集合.
现在开始证伪“定理:ω1是基数”:
反驳:
(A) 定理中对ω1的定义及证法违反了定义论的基本原则之一被定义式(作为单位的整体)不能出现在定义式中.或不能出现在定义式的主变元中,所以
1)ω1的定义应改为如下二式之一;


2) 证明中不允许把ω1返回到右边的α或ω,如果返回ω,ω改为ω1,则被定义式就是ω2了.
例2 对于自然数的定义式:
n+1:{x|N(x)∧x≤n∧in(n+1,n)}={0,1,2,…,n},
其中N(x)读x是一自然数.
我们不能用反证法去证明n+1不是自然数.
(B) 那么ω1究竟是什么呢?它仍是可数集合.分3种情形论证:
情形I 由定理2.32[1]44知它是一极限序数,定理1.4[1]68知,是传递的(其元素即子集)无最大元,有ω1=∪ω,即有



α∈β↔α⊂β且α⊂β↔α⊂β,α≤β↔α⊆β,

情形IIω1是一序数集合,由定理1.7[2]285,因而是∈连接的由定理1.4[1]68ω1是一序数,由推论16.2[2]283任一序数α,都有三岐性,由∈↔<,每一序数就有了大小关系,这就有了排序性,也就可数(数∈或=的个数,).因而也证明,可数无穷多个可数集合(无论是可数无穷集合或可数有穷集合或已归并为单纯的可数无穷集合)是可数集合.证毕
情形III 定义1.4[4]106V是D.无穷(狄德金无穷)iff V有一真子集等数于V,由定理1.9有ω1中仅有可数真子集,ω1只能与可数真子集等数.ω1也就是可数无穷集合.证毕
(具有讽刺意义的是V是一无穷集合,如是不可数,那么V必须等数于不可数集.作为“不可数集”的真子集连,怎么数都不知道,V怎么与它等数?)而无穷集合的定义却要建立在定义1.4的基础上.又是事实.而ω1是可数无穷集合与可数真子集等数却是合理的.ω1如是不可数集,而其所有真子集都是可数的,却是不满足定义7.3前者等数于后者.矛盾.这也证明ω1不是不可数集.
2 康托尔定理的证伪
康托尔定理是无穷集合中,关于基数理论的层次论的基石,认为存在一列集合其势越来越大,并且是无尽止的,《统一无穷理论》认为无穷集合的势只有一种,可数无穷,即其基数均可数.这在中国引起了极大的争论,我们认为对经典集合论的基石不破,那么新的分明集合论就不稳固.此前还没有人撼动康托尔定理.
我们现在要指出它的论证错误.

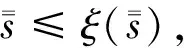
假定不然,亦即存在一双射函数φ:S→ξ(s),对于任一x∈s,φ(x)∈ξ(s),即φ(x)⊆S,当然我们可以问:这一x属于φ(x)吗?首先,令So使得x∉φ(x)的那些元x所组成,即
So={x|x∉φ(x)∧x∈s}
(2.1)
显然So是S的一子集合,即S0∈ξ(S),因为φ是S→ξ(s)上的双射函数,所以在S中必有一元素y,使得So=φ(y).其次我们提出y∈So是否成立这样一个问题.
若y∈So,由(1)得到y∈φ(y).但是,由y的定义,So=φ(y).所以y∈So;
若y∈So,由So=φ(y),得到y∉φ(y),但是由(1),y∈So.
这样,不管y是否属于So,都要导出矛盾,因此,这样的双射函数φ是不存在的.定理5.5得证.
由康托尔的上述定理,立即可以得到下述定理:

2.1 预备知识
现在要说明存在集合S其任一元素也是集合.
定义2.1[1]28对于任一集合x,令X+=x∪{x},称集合X+为集合X的后继.
定义2.2[1]29自然数
0=θ, 再记为So,
1=0∪{0}=θ∪{0}={0}, 再记为S1,
2=1∪{1}={0,1}, 再记为S2,
3=2∪{2}={0,1,2}, 再记为S3,
⋮
n+1=n∪{n}={0,1,…,n}, 再记为Sn+1,
Si,i=1,2,3,…中的元素也是集合.
且有
0∈1∈2∈3∈…
(2.2)
0⊂1⊂2⊂3⊂…
(2.3)
定理2.3[1]37每一自然数都是序数,并且ω是一序数.
定理2.4[1]38任一序数都是集合.
定理2.5[1]38任一序数都是传递集合(即它的每一元的任一元都是它自身的元)即
∀x∀y[x∈y∧y∈s→x∈s].
定理2.6[1]32集合S是传递的,当且仅当∪S⊂S.
定理2.7[1]32集合S的传递性与下述任一条件都是等价的:
1) ∀x[x∈s→x⊂s];
2)S⊂ξ(s).
定理2.8[1]33集合ω是一传递集合,即∀n[n∈ω→n⊂ω].
定理2.9[1]34若x为一传递集合,则x+是一个传递集合x∈y∧z∈x+→z∈x+.
定理2.10[1]34若x是一传递集合,则ξ(x)是一传递集合;
z∈y=∧y∈ξ(x)→z∈ξ(x).
定理2.11[1]34若ξ(x)是一传递集合,则x是一传递集合;x⊂ξ(x).
定理2.12[2]285如果S是一序数集合,则S是∈连接的.
定理2.3[1]44对于任一序数集合S,如果S无最大元的,且S≠φ,则序数∪S是一极限序数.
例3 当α是一非零序数时α是一极限序数当且仅当∪α=α[1]61.众所周知,有幂集的定义ξ(S)={x|x⊆s} 及原则3[1]5对于任意的集合S,都存在S的幂集ξ(x);由定义ξ(S)={x|x⊆s}及原则3[1]5,必有S⊂ξ(S).
由上可知,定理2.1在此结果以后,引出矛盾的论证就不成立.因而康托尔定理的证明是错误的.定理2.1被证伪,定理2.2也就不成立.
我们将在《自然数集合ω幂集ξ(ω)的构成及其子集的可数性》给出ξ(ω)可构造性及其子集的可数性.
3 证伪中“定理5.7[1]123集合[0,1]是不可数的”
[0,1]是否可数,是一个非常重要的问题,一般认为它是连续的,不可数的.我不同意对角线法的证明.
3.1 预数知识;[0,1]与0,+∞]的表达
3.1.1 [0,1]有2ωo个元素,就记为[0,1]={a0,…,ai,…,a2wo},认为是连续而不可数的.
[0,+∞]一般认为是可数无穷(记为∞)多个元素,就可记为[0,+∞]={a0,…,ai,…,aω}.数学中不记[0,+∞],认为∞不是数,只记为开区间(0,+∞).我们认为[0,+∞]的表达正确,理由如下:
集合论中用结构<ω,0,y+>来表达对于0及对y的后继即y+是封闭的.用公式表达为:
ω={x|∀y[0∈y∧∀z[x∈y→z+∈y→z+∈y]→x∈y}
(3.1)
由于在集合论中x∈x+⟺x⊂x+⟺x
3.1.2 数的一个模式:实数的十进制位权表示.
p∞·10∞+…pn·10n+…p2·102+p1·101+p0·100·p-1·10-1+
p-2·10-2+…+p-n·10-n+…p-∞·10-∞,
实数的十进位表示:
p∞…pn…p2p1p0p-1p-2p-np-∞,
我们看到进位单元均为“1”,小数点“.”前p0左右的“数字母”的位数都相等,对称于p0都是无穷位.这是一种镜像关系p0两边的可变换如下:
p∞·10∞+…pn·10n+…p2·102+p1·101+p0·100
(3.2)
p-1·10-1+p-2·10-2+…+p-n·10-n+…p-∞·10-∞
(3.3)
(1)·10-∞:p∞·10∞-∞+p∞·10∞-∞+…+p1·101-∞+p0·100-∞
p∞·100+p∞·101+…p1·10-∞+p0·10-∞
(3.4)
l(p0·100+(2)·10∞:p0·100+∞p-1·10-1+∞+…+p-∞·10-∞+∞=
p0·10∞+p-1·10∞+…p-∞·10-1+p-∞·100
(3.5)
其中“∝,∞”相当于“…,n-1,n,…”或“…,n,n+1,…”只是表达形式的不同.
当我们把实数q=0.p0p1p2…变换为自然数时q=p0p1p2…,我们不用(p0·100+(2))10∞而直接用(2)·10∞,即直接去零(因为对于无穷位而言“p0”与小数点“.”只差一位,几乎相等),就是允许的了.这种镜像关系是孪生关系,即有一个0.x∈[0,1],则必有一个在小数点前的x自然数存在有x∈[0,+∞],因而[0,1]中的所有元素对应{0,+∞]中的无素且一样多.
3.2 “集合[0,1]是不可数的”的证伪
3.2.1 要证伪“集合[0,1]是不可数的”.先要叙述原定理,为避免有断章取义之嫌,照抄全文如下:
定理5.7[1]123(伪定理)集合[0,1]是不可数的.
证明 假定[0,1]是可数的,并且枚举它的所有元素为a0,a1,a2,a3,…,我们知道,在0与1之间的每一实数都可以表示为形式如
0.p0p1p2p3…
(3.6)
那样的无穷小数,其中0≤pi≤9,i∈ω.0≤pi≤9,i∈ω.
a0,a1,a2,a3,…
(3.7)
便可表示为
a0=0.p00p01p02p03…
a1=0.p10p11p12p13…
a2=0.p20p21p22p23…
(3.8)
a3=0.p30p31p32p34…
其中对于任意的i,i∈ω,都有0≤pii≤9.现在构造一数q,使得(3.9)成立.
显然,1)与2)成立.因为对与每一i∈ω,qi≠pii,所以q≠ai这就是说(3.7)式并没有枚举了[0,1]中所有元素.因此假定[0,1]可数就获得了矛盾.这样,[0,1]是不可数的.
如果,此定理成立,则《统一无穷理论》失败,两者必居其一.
对角线法简而言之:
1) 假定A是B; 2)C∈A,且;3)C∉B;4)则A不是B.
假定A是B,即∀x[x∈A→x∈B],也即A⊆B,因而x∉B,则x∉A,如x∈A,就矛盾,A∉B,即A不是B.
(B1) 对于一个小学生还不清楚[0,1]与[0,+∞]=ω谁大的情况下,可能认为[0,1]=ω是可数的,不要说,还有大人这样认为呢,这就是说真的A=B,3)就不成立了.
(B2) 真的A=B成立,在没有理由使c∉B,同时又c∈A,而硬把2),3)绑在一起,那就要推翻对角线法了.
对于对角线的论叙,我们的反问有二:
(H1) 第一句“假定[0,1] (记为A)是可数的(记为B);第二句“并且枚举它的所有元素为a0,a1,a2,a3,…,”第二句话就有问题:
1) 是指真实枚举完全了它的这个[0,1]即A,
2) 如果枚举的是可数的部分即B,这第二句就要改写为:“可数的(即B)元素记为“a0,a1,a2,a3,…,”,如果是前者(即1)中的[0,1],那么“(3.7)式并没有枚举了[0,1]中所有元素”这句话就是不正确的.1)与2)就有矛盾不能同时成立.如果是后者即枚举是B,则1),2)就无矛盾.于是我们认为(01)应表为:假定[0,1]是可数的,又可数的所有元素记为a0,a1,a2,a3,…, “(3.7)式并没有枚举了[0,1]中所有元素”(即ω∈[0,1])这句话就是正确的.这样1)与2)就无矛盾.而假定[0,1]可数(即A⊆B)就有了矛盾.

3.2.2 对角线法证伪(一)
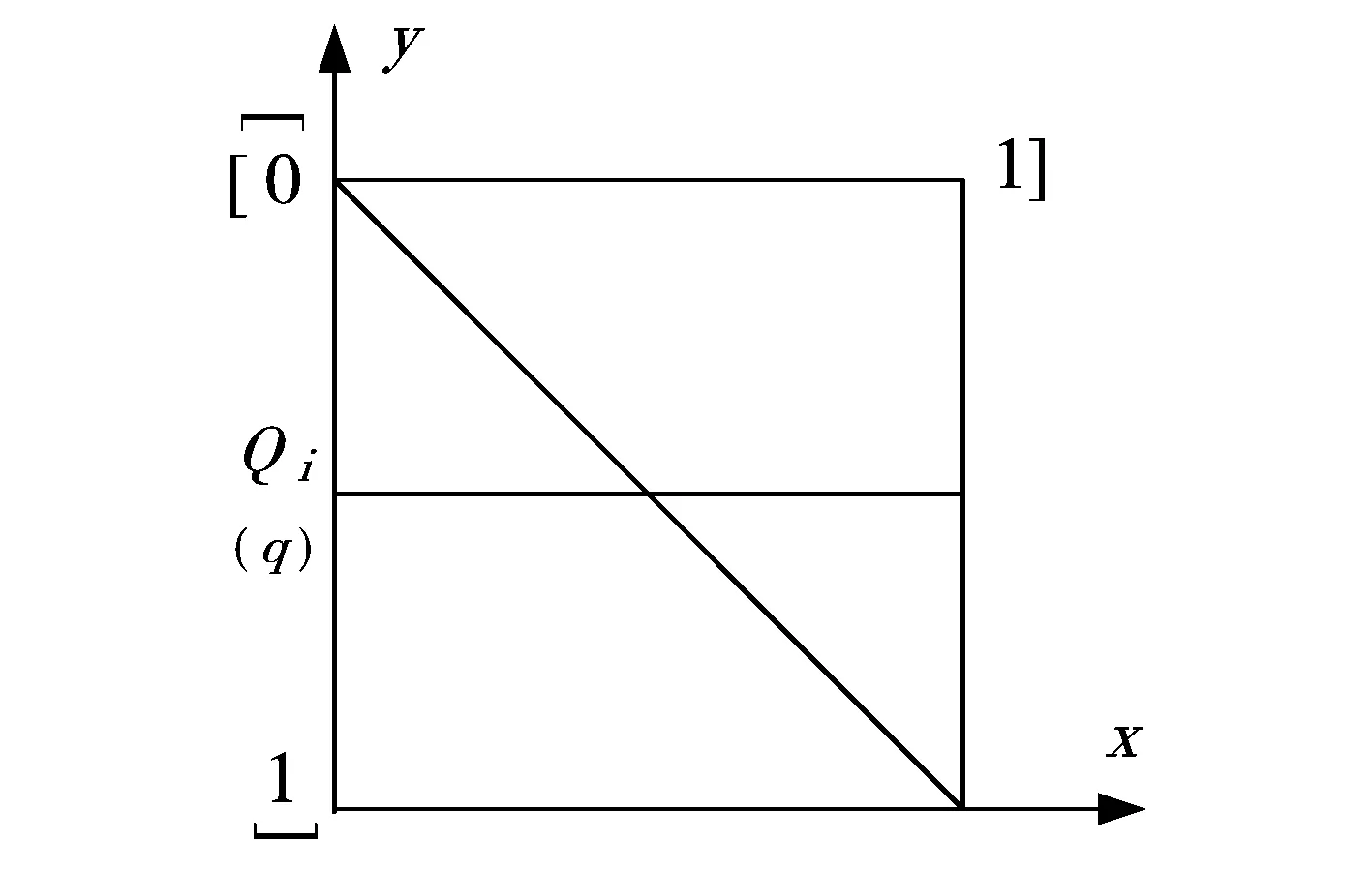
图1 [0,1]×[0,1]方块示意图
对角线法,有这样的功能,不管你的系统有多严密无缝,它也要插进来,因而它会,不断的否定已否定的,包括它刚才(如1.1中的伪定理)所否定的东西,如“不可数的东西”.
我们只用几何直观图形表达来说明:
这是一个方块,高×宽=[0,1]×[0,1],黑体字表示是比连续统[0,1]×[0,1]还要密的的极限:天衣无缝.即水平线之间,没有嵌入的余地.那个q与对角线的交点pii,因为康托尔的定义q=0.q0q1q2q3…qi…而知qi=pii,由对称性,这是一个方块.由康托尔对q的定义:其中对于任意的i,i∈ω,都有0≤pij≤9.现在构造一数q,使得[1]123
1)q∈[0,1],
2)q不等于图表一中的任一数(任意一条水平线)即:令
(3.9)
“q不等于图表一中的任一数(任意一条水平线)”含义有二:
(C1)q在方块的缝隙中;(C2)q在方块外;
方块天衣无缝,“(C1)q) 在方块的缝隙中,不可能”而事实又是q=0.q0q1q2q3…qi…,i∈ω其中小数点以后的数字由4,5两数组成,0≤qi=pii≤9必有0≤q≤1,则q必在方块中;也是康托尔制作q时的要求1) 在方块内,这与(C1)相矛盾.
“(C2) 在方块外”;由于我们可用非m进位制,用并集生成后继法:方块外没有矩阵,q不可能落在方块外,所以(C2)不成立.因此,康托尔对角线法,不可取,
形象地说:它是一根水平的导线垂直移动,只要接触“对角斜线”的每一点(已建成的线与斜线的交点的),都亮红灯,它是说,我不与已建成的所有水平线线重合,也不在缝中(因为它天衣无缝),它又说:我属于这个方块,即q至少与方块中的一条水平线重合,得出矛盾.所以对角线法不成立.
3.2.3 对角线证法的证伪(二):“[0,1]不可数”之再否定.
用如下的记法1),2):
1) 在[0,1]中,的元素有10ω0=2ω0个,我们已经列举完毕了所有元素它为
{a0,…,ai,…,a2ω0],其中a0=0,…,a2ω0=1 (表示有2ω0个元素,没有遗漏);
2)q的构造同前,(q作为一个元是一个序列,在方阵中呈直线形,与对角线相交于一点,
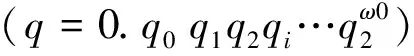
(3.10)
⋮
已有结果定理3.1[1] 123集合[0,1]是不可数的,现在只把原证明的“假设可数”改为“假设不可数”,重抄证明.得如下:
伪定理“[0,1]不可数”之再否定.
证明假定[0,1]是不可数的,并且枚举它的所有元素为a0,a1,a2,a3,…,我们知道,在0与1之间的每一实数都可以表示成为(3.6)的形式.那样的无穷小数,其中0≤pi≤9,i∈ω.a0,a1,a2,a3,…
详细证明见定理5.7[1]123.
显然,1)与2)成立.因为对于每一i∈ω,qi≠pii,所以q≠ai,这就是说,(3.7)式并没有枚举了[0,1]中所有的元素.因此,假定[0,1]不可数就获得了矛盾.这样[0,1]并非不可数的.即也否定“不可数”.比不可数还不可数.
由3.2.1-3.2.3 对角线法用于[0,1]证明不可取.
3.3 用对角线法证明伪定理:“ω(=[0,+∞])是不可数的”
3.3.1 [0,+∞]常在自然数系中表示为{0,1,2,3,…,}或{0,1,2,3,…n,n+1,…,}简记为ω.认定为可数无穷的. [0,1]与[0,+∞]在中学生中那个可数那个不可数,就要要拿出明白的东西来说明,如果用后者[0,+∞]代替前者[0,1]用对角线法,一样可证得“[0,+∞]是不可数的.”
令[0,+∞]为可数无穷的,用上证法得,它是不可数的.现在来证明:
伪定理1ω不可数.
证明假定ω是可数的,并且枚举它的所有元素为a0,a1,a2,a3,…,我们知道,在0与ω之间的每一自然数都可以表示成为形式如下(其理由见1.2)
(其实我们可以直接按 (3.8)去掉“0.”变为(3.12)证明同理).
于是
a0,a1,a2,a3,…
(3.11)
便可表为:
a0=p00p01p02p03…
a1=p10p11p12p13…
a2=p20p21p22p23…
a3=p30p31p32p33…
(3.12)
⋮
其中对于任意的i,i∈ω,都有有0≤pij≤9.现在构造一数q,使得(3.9)成立.
显然, 1)与2)成立.因为对于每一i∈ω,qi≠pii,所以q≠ai,q≠ai这就是说,式(3.11)并没有枚举了[0,+∞]中所有的元素.因此,假定[0,+∞]可数就有矛盾.这样[0,+∞]就不可数.
对角线法同样能证出ω={0,∞}不可数,那它还有何用?
3.3.2 依1.2这是镜像表示法,p0作为个位左右两边是对称的,位数相等,于是相对于(3.6),有
P0表示,就有自然数的镜像表示
…0pn…pi…p3p2p1p0
(3.13)
那样的十进制ω位无穷正整数,其中0≤pi≤9.i∈ω.如:…0369, “,”号之前一位表示“个位”向左依次为十百,这里“…0”表示此前再没有非零的数了.于是
a0,a1,a2,a3,…
(3.14)
如果实数用十进制位权表示为:
lp00·10-∞+…pn·10n+…+p2·102+p1·102+p0·100+p00·10-1+
p01·10-2+…+p0n·10-n+…+p0∞·10-∞,
用十进位表示法:
p00…pn…p2p1p0p00p01p0n…+p0∞.
显然小数点前p0左右两边的位数可以是对称的.p0与小数点只差一位,对于无穷位来说,可以认为小数点两边的位数几乎相等,因此我们就有了(3.13)的表示法,即把(3.13)轴对称地看作为(3.6).这是镜像表示法: [0,1]的数的量与[0,+∞]的位数的量是一样多的.[0,1]中a0,a1,a2,a3,…各不相同,其映照的镜像[0,+∞]也各不相同,且数量一样多.这样(3.14)便可表示为:
…p03p02p01p00,=a0
…p13p13p11p10,=a1
…p23p22p21p20,=a2
…p33p32p31p30,=a3
(3.15)
⋮⋮⋮⋮⋮
其中对于任意的i,i∈ω,都有0≤pij≤9.现在构造一数q,使得·
1)q∈ω,
2)q不等于(5.9)中的任一数,
令
(3.16)
显然,1)与2)成立.因为对于每一i∈ω,qi≠pii,所以q≠ai这就是说,(3.14) 式并没有枚举了ω中所有的元素.因此,假定ω可数就获得了矛盾.这样ω就是不可数的
对角线法能证出ω={0,∞}不可数,那它还有何用?
注不过即使是ω,用对角线法,只是.证出的元素多了一个,从序数的角度大小,有ω⊂ω+1=ω∪{ω}={0,1,…,ω}二分反证法,在此不灵了.
在集合论中,自然数与序数的编码,用的是非m进位制,用的是并集生成后继法:
n+1=n∪{n}={0,1,2,3,…,n};ω={0,1,2,…,n,n+1,…},
其生成函数是“+1”, 0是初始函数;
人类的记数法;有个特点1).个位在右,高位在左;2).读数又是从左读起,高位先读:
如:139读“一百三十九”,而不读“九三十一百”
ω表示为方阵,数据自上而下排队列,有2种方法:
1) 左竖向首位对齐:(对角线为最高位); 2) 右竖向个位对齐,(对角线为为0位)
0={},
0={}
1={0},
1={0}
2={0,1},
2={0,1}
3={0,1,3},
3={0,1,3}
4={0,1,2,3},
4={0,1,2,3}
5={0,1,2,3,4},
5={0,1,2,3,4}
6={0,1,2,3,4,5},
6={0,1,2,3,4,5}
7={0,1,2,3,4,5,6},
7={0,1,2,3,4,5,6}
… … … …
ω这种编码,也可说是“一进制”编码,其集合表示为N(1),有6ω(1)=ω个元素.所以它是一个方阵(方阵外没有矩阵),其对角线的元素qi=pii现在我们来分析,对角线法;显然方阵是[0,+∞]×[0,+∞]也记为ω其高度就是元的个数∞(ω对∞封闭),没有矩阵包含它.现在我们相对于3.1的伪定理1(ω不可数),来证明下面相反的结果.
3.3.3 定理2: 对角线法不能证明“集合ω是不可数的,”

图2 [0,+∞]×[0,+∞]方阵示意图
证明假定ω是可数的,并且枚举它的所有元素为a0,a1,a2,a3,…我们知道,在0与∞之间的每一自然数都可以表示为形式如
p0p1p2p3…
(3.17)
那样的无穷自然数序列,其中0≤pi≤9,i∈ω
a0,a1,a2,a3,…
(3.18)
便可表示为
a0=p00p01p02p03…
a1=p10p11p12p13…
a2=p20p21p22p23…
a3=p30p31p32p33…
(3.19)
⋮⋮⋮⋮⋮
其中对于任意的i,i∈ω,都有0≤pij≤ω,i∈ω.现在构造一数q,使得
1)q∈[0,ω]×[0,ω],
2)q不等于(3.18)中的任一数,
令
其实只要,q是所有条水平线的与对角线的交点的数码,变号相异投影到q,q在上下移动时,它就不再与对角线相交,也就不再与ω的任一条水平线重合;这个方阵外没有认可矩阵包围,因此q也不在方阵外认可的矩阵中,因而1)与2)不可能同时成立.这样就不可能证伪:“假定ω是可数的”,也就是对角线法不可取.
由3.3.1~3.3.3 对角线法对于[0,∞]不能用.
由3.2与3.3对角线法对于证明[0,1]与[0,+∞]的可数与否是不可取的.
自然数集ω(N)的区间定义如下:
N∀qi∀q[q∈N↔(q=q1q2q3…qi…∧i∈ω∧0≤qi≤9)];
读:“满以足下条仵的N,对一切qi与q而言,q属于N当且仅当由qi组成,可以可数位无限长(i∈ω)且q为0至9中的任一数.,” 自然数N(或ω)认定为可数的.如果可数的集合(在本文中记为B):B=N={α1,α2,α3,…,αi,…,α∞},那么“2)q不等于(3.7)中的任一数.

的作法”就不成立.改来改去0≤qi=4或5≤9,q仍在B中.这样就不可能反驳“假定ω是可数的”,也就是对角线法不可取.
同样我们可以定义实数如下:
R∀qi∀q[q∈R↔(q=0.q1q2q3…qi…∧i∈ω∧0≤qi≤9)];
读:“满足以下条件的R,对一切qi与q而言q属于R当且仅当q由0.以后qi组成,可以可数位无限长(i∈ω)且qi为0至9中的任一数.”称R为实数集,这是一个新定义.
同样对于[0,1],用对角线法来证明可不可数,对于下述两种情形:
1) 当定理描述为: [0,1]是不可数的,
证明(开始是) 假定[0,1] (记为A)是可数 (记为B)的,
2) 或定理描述为: [0,1]是可数的.
证明(开始是) 假定[0,1](记为A)是可数 (记为B)的.
由3.1.2 镜像关系与孪生关系的道理可知[0,1]与[0,+∞]的元素是一样多的.只要令B:R(或ω)={α0,α1,α2,α3,…},对角线法也一样不起作用.
4 关于连续统假设的一个新证明2ω0=ω0.
“连续统问题近一百年来,虽然经过许多著名数学家的努力,取得了几项重大进展,但并未完全解决.…,仍有不少著名数学家为它的答案不懈地努力”[1]126提醒我们,用新的方法来解决才有出路.何华灿何智涛创立的《统一无穷理论》是集合论的突破,创新与完善是新的里程碑.连续统假设是指2ω0=ω1被称为第一个不可数的基数.现在我们要证明 2ω0=ω0,即2的ω0次幂,仍是可数的.
4.1 {0,1}ω0的元的编码与计数;作为ω之上的最小基数2ω0=ω0.
依自然数的定义2:={0,1}则{0,1}ω0=2ω0,如何对{0,1}2,{0,1}3,{0,1}4,的元进行编码这难为了人的思路;现在有了一个新的想法,用二进制:我们要归纳地证明;
定理1 2ω0=ω0.
奠基: 0,1,2.
0){0,1}0={0}二进制表示: 元的编码(是序数) {0}=1 基数(元的个数1).
1){0,1}1={0,1} 二进制表示不变:元的编码(是序数) {0,1}=10 基数(元的个数2).
2){0,1}2={0,1}×{0,1}二进制表示:
{0,1}4 3 1
×{0, 1}
元的编码(是序数) {00, 01, 10, 11}=100 基数(元的个数4).
注;这是底乘后置法.再举几个例:
3){0,1}3={0,1}2×{0,1}二进制表示:
{00,01,10,11}
× {0,1}
——————————————————————————————————
元的编码(是序数) {000,001,010,011,100,101,110,111}=1000基数8.
4){0,1}4={0,1}3×{0,1}二进制表示:
{000,001,010,011,100,101,110,111}
× {0,1}
——————————————————————————————————
元的编码(是序数) {0000,0001,0010,0011,0100,0101,0110,0111},
10进制翻译 0, 1 ,2 ,3, 4, 5, 6, 7
{1000,1001,,1010,1011,1100,1101,1110,1111}=10000基数16.
10进制翻译 8 ,9,10,11,12,13,1,4,15,16
我们已经看出,序数列之首项均是0,尾项都是1.基数均是 一个1后是几个0.于是归纳假设:

归纳证明:

归纳结论:

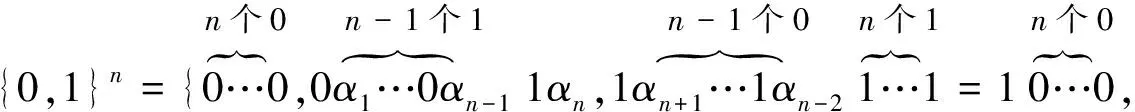
b) 递归构成

(*)
10制表示为{0,1,2,3,4,…,7,8,…,2ω0-1=2ω0.
{0,1}ω0作为超积理解如下:超积(也称超乘积或广义笛卡尔积)[2]187其表达式为:


(**)
(*) (**)同一,只是表示不同.
8) 现在来证明{0,1}ω0=ω0.用m进制n位的编码表示的自然数集合,有mn个编码,其最高编码值,记为Maxv(x),令N(m)n表示m进制n位的编码的集合,对于二进制有:
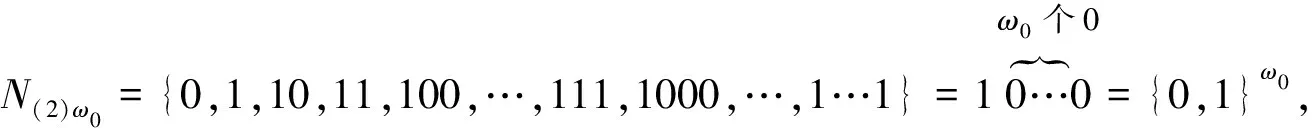
对于十进制有:


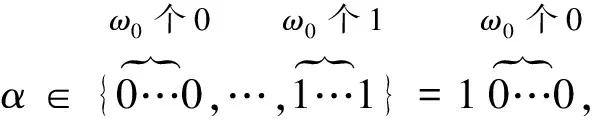

我们理解自然数十进制的序数表达与性质:
{0,1,2,…,i,…,n}=n+1;i∈n+1,i 这也适合二进制.等式右边的n+1,ω是等式左边的∈连接的,传递集合的最小上界[2]287. 2ω0={0,1}作为超积,我们采用底乘后置法,运算结果,给出了自然次序,这是契机. (H2) 由3)、4)可见,如果3)中的序数是{a1,a2,…,an}其长度是偶数,则经过×{0,1}后,4)式是把3)式每项左端先加0;接着再在3)式每项左端加1;即有: {0a1,0a2,…,0an;1a1,1a2,…,1an}, 其项数多了一倍.注意到a1均为0,an均为1,也即首项均为0,末项均为1,“=”号右边(是基数)为一个1后面均是0;对于很长或无穷序数序列,我们就不必细究“=”号左边,中间的项,具体是什么了. (H3) 以2A,A={a,b}为例,作一些语义上的说明. 注:100=4;左边的序数再大,大不过右边的基数(最小上界),这里11<100. 表左下角的矩阵称为表示矩阵,正是本文使用的形式,它是可以代表右下角的,0表示A中对应的(列的顶元素)元素不出现,1表示对应的(列的顶元素)元素出现.矩阵的每一行是二进制序数(这个序数也是从0算起.),每一项中出现1的个数为子集的元的个数. 当A:=ω时,也作这样理解. 进制的位权解释:如字x=xn…xi…x3x2x1;ki-1称为数xi的位权,k为进制,i-1为右起的数位;于是X的位权解释:[x]=xnkn-1…xiki-1+…+x3k2+x2k1+x1. 对于十进制我们有:令A(10)={0,1,…,9}, 进制的位权解释:如字x=xn…xi…x3x2x1;10i-1称为数xi的位权,10为进制,i-1为右起的数位;于是x的位权解释: [x]=xn10n-1…xi10i-1+…+x3102+x2101+x1. 令N={0,1,2,…,n,n+1,…,∞};有字x1=x∞…xn…x3x2x1;于是x1的位权解释: [x1]=x∞10∞-1…xn10n-1…+x3102+x2101+x1; 正实数的十进制表示与位权解释:无穷大与无穷小的对称性及可数与连续统的同一性. 令 此乃集合的极限对表示法,这里的极限指编码位n,不是指该编码位的最高值[n]. 有字 (*2) 第二行可写为: 表示小数点右向,即反向的数符及位权.是很形象的.此式说明两点 1) 由(*1)后继函数S=+1,在字的进位制单元是不变的,为1; 3) 注意δ只是小数点右边的权位解释下的单元,而进位制的单元匀是1. 这就是通常的算术解释.从数制的角度看,可数的,就止于此.完整的正实数谱[2].其中心思想是,通过一个带小数点的实数范式的小数点两边的区间的字长相等来证明{0,1}与{1,∞}都是可数的. 5.3.1 自然数集是人类以十进制记数的方法而表达的: 事物个数本无编码:⊙,|,| |,| | |,| | | |,| | | | |,…,| | | | | | | | | 用十进制表为: 0,1,2,3, 4, 5, …, 8, 9, 用二进制表为: 0,1,10,11, 100, 101,…, 1000, 1001, 用十进制表为: 10, 11, 12, 用二进制表为: 1010, 1011, 1100. 5.3.2 这种数制表示,其实有一种K进制表示函数σ,对于十进制用复迭式表达. 如: 0, 1, 2, 3, …,8, 9, 10, 11, …, 19, 20, 5.3.3 用方幂表示自然数,底表示进制,方幂为位数,对于十进制,来证明10ω的可数性:有 10ω:100,102,101,103,…, 10n, 10n+1,…, 5.3.4 用二进制表示自然数集,来证明2ω的可数性: 对于2ω也有同样的结论.仅是记数法的不同: 这里底2是用十进制符号代二进制符号,用二进制符号表为10ω. 十进制: 0, 1, 2, 3, 4, 5, 6, 7, 8,…, 二进制: 0, 1, 10, 11, 100, 101, 110, 111, 1000,…,n,n+1,… 由此二进制与十进制有同样的结果: 1, 2, 4, 8, 16, 32,… 十进制表示: 2ω: 20, 21, 22, 23, 24, 25,… 二进制表示:10ω:100,101,102,103,10100,10101,… 注:十进制中16=222,对应于二进制圾示中的10000=101010,如此等等. 本文三的核心思想是可数无穷集合的无穷子集也是可数无集合. 但上述的可数无穷的定义,还不够明确. D1集合可数的定义:S是可数的当且仅当,存在一开始函数或首元α(∃x[x∈S∧f(x)=α),且有一生成函数f使得n∈S→f(n)∈S,如果有最大元M,且M≠∞,称可数有穷,否则称可数无穷的(这个否则包括;最大元是∞,或无最大元);并作如下确认: (D1) 开始确认 1) 非ω自然数(如4={0,1,2,3}是可数有穷集合, 2)ω是可数无穷集合; (D2) 后继确认 这称为确认定义,这样我们的讨论就有了依据.[0,1][0,∞]就可确认了.[+∞,-∞]常表示为实数,如果允许可以细致表示为[+∞,±0,-∞]=[+∞,+0][-0,-∞]. 这个定义辨论双方是否合意?如何改正或者让它去不加定义?总是不好.但实际又是这样在做的,以前的定义可以说是经典集合论的内部定义只涉及{0,1,2,3…}可数无穷,{0,1,2,3…}可数有穷,并认为没有{0,1,2,3…}表示的必要.但经典集合论中有[0,1],[0,+∞]这样的集合表示,新的定义照顾了各方,我们在讨论的时候就有了依据. 由上可见,可数是用自然数作样板来数的.而自然数是什么呢? 定义6.3[6〗28对于任意集合x,令x+=x∪{x}称集x+为集合x的后继.(笔者注+是一后继函数). 皮阿诺(Peano)自然数公理[1]31是很有名的,简单说来,它是关于自然数0和后继运算以及集ω上的结构的,人们也常记做〈ω,y+,0〉: 1)∀[x∈ω→x+≠0], 2)∀[x,y∈ω∧x+=y+→x=y], 3)∀[x∈ω→(A(x)→A(x+)]→∀x[x∈ω→A(x)],ω归纳原则,但从集合论的集合的角度[6]29更恰当的表述: 无穷集合存在公理;存在这样的集合ω: 1) 0∈ω∧∃x[x∈ω∧x+=0], 0是ω的(开始函数)首元. 2)∀x[x∈ω→x+∈ω],ω对其中任一元的后继是封闭的. 3)∀x[x∈ω→(x=0∨∃y[y∈ω∧x=y+],ω的最小性, 1),2)称ω是一归纳集,3)说ω是归纳集合中之最小者. 注意:0是ω的开始函数,也叫首元,并且这里还有一个后继函数,我们,称之为生成函数,这是递归函数论的观点.我们现在正式命名ω为可数无穷集.这样我们用一一对应法,依样版,就可照样裁衣.称其它的为可数的了. 不可数为伊始,还有高阶不可数,这种东西,在数学上没有用,在生活中没有用,在计算机上更无用;计算机上可数无穷都要通过步长中止,特殊字(条件)中止与自然中止,用四舍五入来近似. 对角线法对于十进制表示的集合不能用;展示十进表示的数的竖向序列呈竹杆形.每进一位,其高度是前一位的十倍.方阵对角线何在.这是实践得出的结论,人脑进制进位法与算盘、计算器、计算机不同,后者的,9位数是预先设定的,位数有一定的容量.而人的定位是随机的,我在这里要说明“进制”与 “方幂”的关系,自然数只要数下去,就会达到无穷位,十进制就有10ω,二进制就有2ω,而且,很重要的一条是:一开始直至你还在操作着,就还不是无穷位.但它无穷的进行下去,而2ω这个[0,1]的元 999 数也就可数无穷了, 这命名为“[0,1]的进制可数证明.”,人们常说“实践证明”,这是我们所见的事实,列宁说是“千万次形成的实践的格”.公理是不加证明的,乃实践证明也.进制的ω无穷次方就是这样来的.见如下: 0 (1) 1 零阶100 (9) 10 一阶101 ⋮(90) 99 100 二阶102 ⋮(900) 1000 三阶103 ⋮ (9000) 9999 10000 四阶104 所以10ω:100,101,103,…,10n,10n+1,…二进制的也一样有: 2ω:20,21,23,…,2n,2n+1,…这不是所谓连续统[0,1]的元数吗?可它是数出来的. “一一对应”是研究无穷集合的主要方法,光有方法不行,还要有工具,它的度量.工具的尺是ω!数数要有尺!现在开始用尺ω来量: ω: 1, 1, 2, 3, …,n,n+1,…, 2ω: 20, 21, 22, 23,…,n,n+1,…, 10ω: 100, 101, 102, 103,…,n,n+1,…,, mω:m0,m1,m2,m3,…,n,n+1,…, ωω: 00, 11, 22, 33, …,n,n+1,…, (6.1) ↓ ↓ ↓ ↓ ↓ (6.2) ↓ ↓ ↓ ↓ ↓ 2ω: 20, 21, 22, 23, …,n,n+1,… (6.3) ↓ ↓ ↓ ↓ 1, 2, 4, 8, …,n,n+1,…,显然它是可数的; 又显然有: (6.4) 2)上述函数,的变项我们不用x,因为它论域未定,不用n,因为它是有限值; 3)上述函数,与ω是一一对应的,都有逆(向)函数,即反函数. 4) 式(6.2)与式(6.3)是互逆的,有双射; 5) 式(6.2)与式6.4)分母的含义是把“1”个东西“[0,1]”,无穷的一分为二(常用两个半区间表达),作为细粒度,去与分子这个整体1=[0,1]去比较,来认识整体的容量的大小.而这个 “1”就是所谓的连续统[0,1],又(6.3)就是它的量. 6)F(ω):F(0),F(1),F(2),…,F(n),F(n+1),…F(ω)=dfF(x), 7)ωω:00,11,22,33,nn,n+1n+1,…,一看就知这是可数的,用不着证明呢.定理3.4[1]65. 我们在证伪了“对角线法对于[0,1]的不可数”之后,按照直觉主义的观点:[0,1]可不可数还是未定的,必须要有正面的证明,就是说,要在经典集合论中证明[0,1]的可数.而且现在不是连双方均有人认为:经典集合论的领域理论中,实数是不可数的吗? 式(6.1)~(6.4)相等,并见说明1)-6);得到式(6.3)等于2ω,如何证明它是可数.这个,希尔伯特,在数学大会上的二十三个问题的第一个,要用初等的方法让中学生能看懂就好了;人们希望用一一对应法证明. 定理1 [0,1]是可数的. 2) 这个容量2ω是可数的,因为它与ω有一双射函数(过去无人作出过): f1:2ω→ω,log22ω→ω,log22ω=ω,log220=0,log221=1,log222=2,…; f2:ω→2ω;g(2,ω)=2ω,g(2,0)=20,g(2,1)=21,g(2,2)=22,…,20=1, 推论6.1 连续统假设,相对于ZFC,是不独立的 证1)上述定理一已证明与ω无穷公理 (它是ZFC的一条) 有关,是在ZFC系统内证明的; 2) 只要涉及ω与其一一对应,就与ZF有关,所谓独立性的证明模型,处处用到ZF,怎能么能说与ZF无关.(人们认为用一个模型M,既证出A又证出A,就认为与M独立或无关,难道人们不能用反证法观点,去否认选取模型的的恰当性). 致谢作者感谢在学术上给予提携的恩师张锦文! 感谢桂起权教授对本文的审阅和推荐! 参考文献: [1] 张锦文. 公理集合论导引[M]. 2版.北京:科学出版社, 1997. [2] 张锦文. 集合论浅说 [M]. 北京:科学出版社, 1984. [3] 张锦文. 集合论与连续统假证浅说 [M].2版. 上海:上海教育出版社,1982. [4] 程极泰. 集合论 [M].北京:国防工业出版社,1985. [5] 何华灿, 何智涛. 统一无穷理论 [M].杭州:笠学出版社,2011. [6] 莫绍揆. 归函数论[M]. 上海:上海科学技术出版社,1965. [7] 莫绍揆. 归论 [M].2版. 北京:科学出出版社, 1997.
5 用进制法证明2ω可数
5.1 K进制后继函数:令A={01,…,0k},字的K进制后继函数如下[1]87:



5.2 再次证明连续统的可数性,即{0,1}与{1,∞}都是可数的
5.3 用进制法证明2ω可数



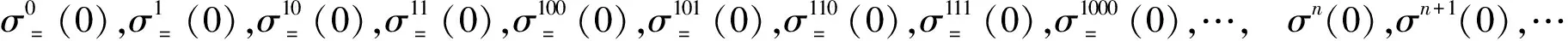

6 用对应法证明[0,1]可数
6.1 可数无穷的定义

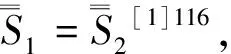


6.2 对角线法再议
6.3 关于一一对应与[0,1]实数区间的可数性