移相干涉图的旋转误差研究

徐萌萌, 左 芬, 邓 洋

(淮阴师范学院 物理与电子电气工程学院, 江苏 淮安 223300)

0 引言

移相干涉测量术,以其非接触、高精度、高效率等优良特点,已然在计量、工业检测等众多领域形成了广泛的应用．移相干涉术拥有诸多优点的同时,许多因素的存在也直接影响了其相关性能指标的进一步提升．比如,激光光源稳定性影响测量精度的重复性;参考波面的精度直接影响测量精度;移相器的非线性对波面相位调制产生误差;探测器电子噪声也会影响测量精度等[1-3]．以上的因素主要来自于干涉仪本身,而事实上移相干涉仪的误差仅有少部分来自于干涉仪器本身,绝大多数来自于环境,比如空气的扰动和环境的振动[4-5]．

在移相干涉中,由于环境扰动导致图像传感器产生的干涉图之间产生微小的相对旋转．这种情况下运用移相算法进行波面恢复时,测量精度将必然降低．因此,在执行移相算法前,需要定量地确定移相干涉图之间的相对旋转角θ．基于以上事实,本文提出了一种在移相干涉术中干涉图之间的相对旋转误差的修正方法．

1 原理

在移相干涉测量术中,移相过程由于环境扰动的存在使得图像传感器产生的干涉图有微小的旋转误差．以第一幅干涉图作为空间方向基准,将其他的干涉图作为方向待定图与之比较．在此,将方向待定图相对方向基准图顺时针旋转称为右旋．反之,称为左旋．

将两幅干涉图置于同一坐标系下,得到各自的横轴方向和纵轴方向上的条纹周期．并据此计算得到两幅干涉图之间的相对旋转误差角θ．在进一步的移相算法中反向旋转θ．

2 条纹周期的计算

如图1,将方向基准图置于一合适的直角坐标系下,在X轴上读取一段固定区域的点光强数据．并对这些数据进行正弦拟合,得到

Ix=Acos(ωxt+φx)

(1)

因此,可得X轴方向的周期

(2)

同理,得到Y轴方向

Iy=Bcos(ωyt+φy)

(3)

(4)

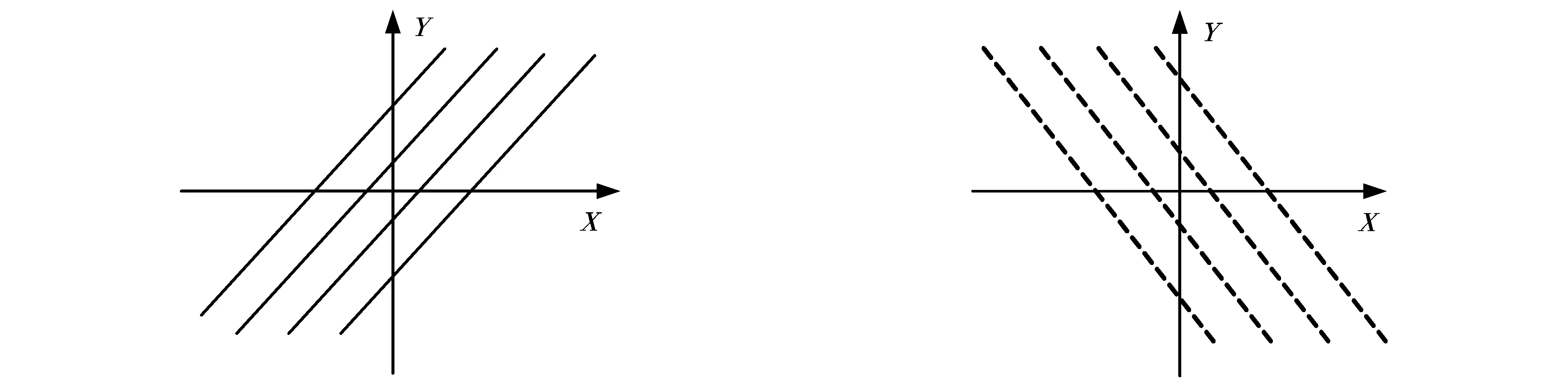
图1 方向基准图 图2 方向待定图

如图2,将方向待定图置于同一坐标系下,在X轴方向上读取一段固定区域的点光强数据,再次正弦拟合,得到表达式

Ix1=A1cos(ωx1t+φx1)

(5)

因此,可得到X轴方向的周期

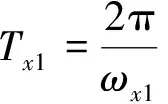
(6)

同理,在Y轴方向,得到

Iy1=A1cos(ωy1t+φy1)

(7)

周期为

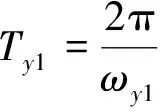
(8)

3 移相干涉图旋转误差角计算

3.1 移相干涉图右旋

图3为右旋干涉图与方向基准图叠加于同一坐标系的示意图,图中实线表示为方向基准的干涉,虚线表示为右旋的干涉．取实线和虚线的一个交点O,以点O为原点．X轴与实线的交点依次为A(-Tx1,0),B(-Tx,0),C(Tx,0),D(Tx1,0)．与虚线表示的干涉条纹交点如图为点E(0,Ty),F(0,Ty1),G(0,-Ty1),H(0,-Ty)．

由图3可知

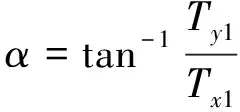
(9)

(10)

由以上两式得到

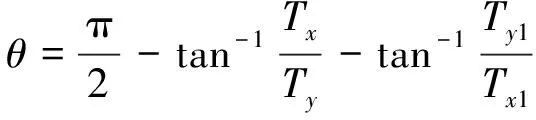
(11)

3.2 移相干涉图左旋

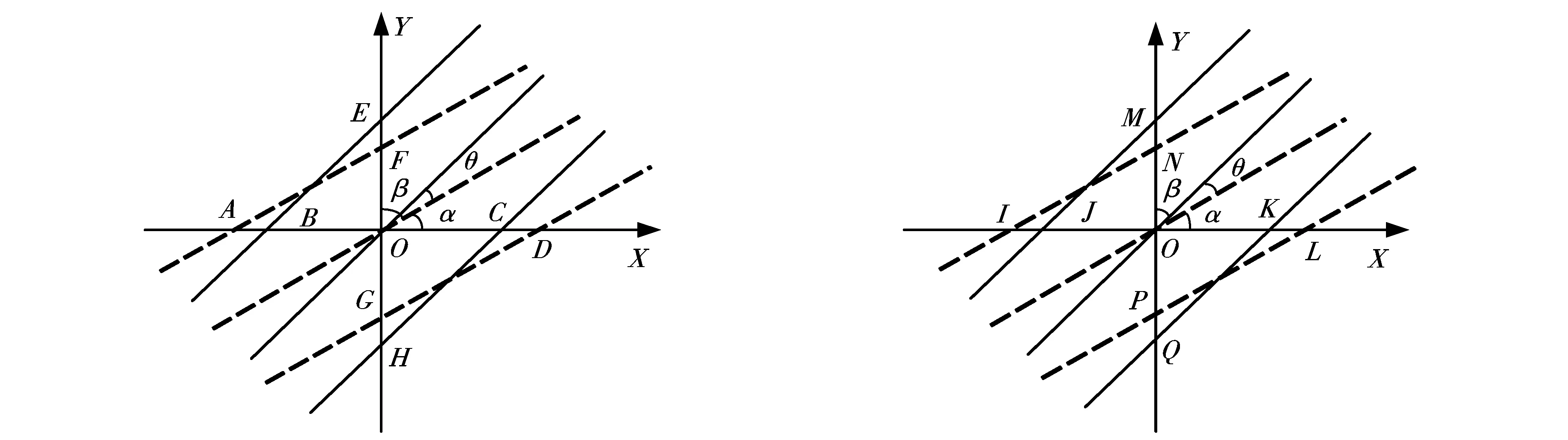
图3 右旋干涉与方向待定干涉的叠加 图4 左旋干涉与方向待定干涉的叠加

图4为左旋干涉图与方向基准图叠加于同一坐标系的示意图,图中实线表示为方向基准的干涉,虚线表示为左旋的干涉．取实线和虚线的一个交点O,以点O为原点．X轴与实线的交点依次为I(-Tx,0),J(-Tx1,0),K(Tx1,0),L(Tx,0)．与虚线表示的干涉条纹交点为点M(0,Ty1),N(0,Ty),P(0,-Ty),Q(0,-Ty1)．

由图4可知

(12)

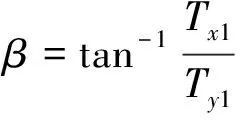
(13)

由以上两式得

(14)

综合以上分析,旋转角θ就是环境振动引起的旋转误差．在移相算法中,相应地将干涉图逆向旋转θ角度以修正旋转误差．

4 结论

环境扰动对移相干涉测量的精度产生重要的影响．本文着重对图像传感器的旋转误差给移相干涉测量的造成的影响进行了深入的理论研究．通过一系列的理论推导,得出移相干涉图之间的相对旋转误差角,以便于在移相算法中消除这方面的误差达到提高移相干涉测量精度的目的．

参考文献：

[1] 左芬. 同步移相干涉测量的抗振技术研究[D]. 南京:南京理工大学, 2008.

[2] 沙定国. 光学测试技术[M]. 2版. 北京:北京理工大学出版社, 2010.

[3] 左芬,陈磊.移相干涉术测量中的抗振技术[J].光学技术.2007,28(4):55-59.

[4] Brunning H. Digital wavefront measuring interferometer for testsing optical surfacesand lenses[J].Applied Optics,1974,13(11):88-94.

[5] 吴栋.移相干涉仪自适应抗振技术研究[D].南京:南京理工大学,2004.