关于丢番图方程x3±64=Py2的整数解的研究

钱立凯, 普粉丽

(1.曲靖师范学院 教师教育学院, 云南 曲靖 655011; 2.普洱学院 数学与统计学院, 云南 普洱 665000)

0 引言

方程

x3±a3=Dy2(x,y∈N,D>0,且无平方因子)

(1)

是一类重要的丢番图方程,其整数解引起了人们的关注.a=1时,管训贵[1]、杜先存等[2-3]已有一些结论;a=3时,钱立凯、杜先存[4-5]已有一些结论;a=4时,目前的主要结论有:1994年,李复中[6]给出D只含一个6k+1型素数因子时丢番图方程x3±64=3Dy2在一些条件下无非平凡解的充分条件;1994年,张海燕、李复中[7]给出D不能被3或6k+1型的素数整除且D≠k+2时丢番图方程x3±64=Dy2无非平凡解的充分性条件;2008年,赵天[8]讨论了丢番图方程x3±23n=3Dy2(D=7,13,19,31)的解;2012年,张攀[9]研究了十个丢番图方程x3±64=py2(p=7,13,19,37,43)的所有整数解.本文主要研究D为6k+1型素数时丢番图方程x3±64=Py2解的情况.

定理1 设P≡5,17(mod24)为奇素数时,则丢番图方程

x3-64=Py2

(2)

无x≢0(mod2)正整数解.

定理2 设P≡5,17(mod24)为奇素数时,则丢番图方程

x3+64=Py2

(3)

无x≢0(mod2)的正整数解.

定理1证明因为x≢0(mod2),而P≡5,17(mod24)为奇素数,故由(2)知,y≢0,(mod2)所以x≡1(mod2),y≡1(mod2),又因为x3-64=(x-4)(x2+4x+16),所以gcd(x-4,x2+4x+16)=gcd(x-4,(x-4)2+12x)=gcd(x-4,(x-4)2+12(x-4)+48)=gcd(x-4,48)=gcd(x-4,3×24)=1或3,从而丢番图方程(2)可以得出下列4种可能的情形:

情形1:x-4=Pu2,x2+4x+16=v2,y=uv,gcd(u,v)=1;

情形2:x-4=u2,x2+4x+16=Pv2,y=uv,gcd(u,v)=1;

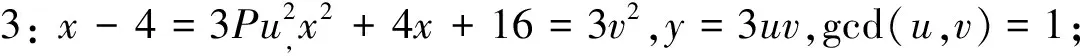
情形4:x-4=3u2,x2+4x+16=3Pv2,y=3uv,gcd(u,v)=1.

下面分别讨论丢番图方程(2)在这4种情形下的所有解的情况.

情形1, 第二式可化为(x+2)2+12=v2,即v2-(x+2)2=12,则有(v+x+2)·(v-x-2)=12,可得x=0或-4,代到第一式可知x=0或-4,均不适合此式,因此该情形方程(2)无x≢0(mod2)的正整数解.

情形2, 第二式可化为(x+2)2+12=Pv2,两边取模3得(x+2)2+12≡Pv2(mod3),又

而

得出矛盾,因此该情形方程(2)无x≢0(mod2)的正整数解.

情形3, 因为x≡1(mod2),知u2≡1(mod2),即u2≡1(mod8).由于由于P≡5,17(mod24),知P≡1,5(mod8),可知x=3Pu2+4≡3,7(mod8),则x2+4x+16≡5(mod8).又因为x≡1(mod2),所以有3v2≡1(mod2),则v2≡1(mod8),所以3v2≡3(mod8),则有5≡x2+4x+16=3v2≡3(mod8),得出矛盾,因此该情形方程(2)无x≢0(mod2)的正整数解.

情形4, 第二式可化为(x+2)2+12=3Pv2,把第一式中的x=3u2+4代入得3(u2+2)2+4=Pv2,两边取模3,得3(u2+2)2+4≡Pv2(mod3),而

得出矛盾,因此该情形方程(2)无x≢0(mod2)的正整数解.

从以上4种情况的讨论,得知P≡5,17(mod24)为奇素数时,丢番图方程x3-64=Py2无x≢0(mod2)的正整数解.

定理2证明因为x≢0(mod2),而P≡5,17(mod24)为奇素数,故由(3)知,y≢0(mod2),所以x≡1(mod2),y≡1(mod2),又因为x3+64=(x+4)(x2-4x+16),所以gcd(x+4,x2-4x+16)=gcd(x+4,(x+4)2-12x)=gcd(x+4,x(x+4)-12(x+4)+48)=gcd(x+4,48)=gcd(x+4,3×24)=1或3,从而丢番图方程(3)可以得出下列4种可能的情形:

情形I:x+4=Pu2,x2-4x+16=v2,y=uv,gcd(u,v)=1;

情形II:x+4=u2,x2-4x+16=Pv2,y=uv,gcd(u,v)=1;

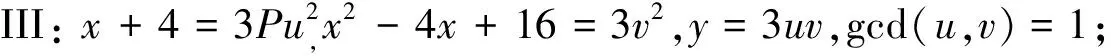
情形IV:x+4=3u2,x2-4x+16=3Pv2,y=3uv,gcd(u,v)=1.

下面分别讨论丢番图方程(3)在这4种情形下的所有解的情况.

情形I, 第二式可化为(x-2)2+12=v2,即v2-(x-2)2=12,则有(v+x-2)·(v-x+2)=12,可得x=0或4,代到第一式可知x=0或4,均不适合此式,因此该情形方程(3)无x≢0(mod2)的正整数解.

情形II, 第二式可化为(x-2)2+12=Pv2,两边取模3得(x-2)2+12≡Pv2(mod3),又

而

得出矛盾,因此该情形方程(3)无x≢0(mod2)的正整数解.

情形III, 因为x≡1(mod2),知u2≡1(mod2),即u2≡1(mod8).由于P≡5,17(mod24),知P≡1,5(mod8),可知x=3Pu2-4≡3,7(mod8),则x2-4x+16≡5(mod8).又因为x≡1(mod2),所以有3v2≡1(mod2),则v2≡1(mod8),所以3v2≡3(mod8),则有5≡x2-4x+16=3v2≡3(mod8),得出矛盾,因此该情形方程(3)无x≢0(mod2)的正整数解.

情形IV, 第二式可化为(x-2)2+12=3Pv2,把第一式中的x=3u2-4代入得3(u2-2)2+4=Pv2,两边取模3,得3(u2-2)2+4≡Pv2(mod3),而

得出矛盾,因此该情形方程(3)无x≢0(mod2)的正整数解.

从以上4种情况的讨论,得知P≡5,17(mod24)为奇素数时,丢番图方程x3+64=Py2无x≢0(mod2)的正整数解.

参考文献：

[1] 管训贵.关于不定方程x3+1=py2[J].淮阴师范学院学报:自然科学版,2011,10(4):304-306.

[2] 杜先存,吴丛博,赵金娥.关于Diophantine方程x3±1=3Dy2[J].沈阳大学学报:自然科学版,2013,25(1):84-86.

[3] 杜先存,管训贵,杨慧章.关于不定方程x3+1=91y2[J].内蒙古师范大学学报:自然科学版,2013,42(4):397-399.

[4] 钱立凯,杜先存.关于丢番图方程x3±27=py2[J].西南民族大学学报:自然科学版 2013,39(4): 580-581.

[5] 钱立凯,杜先存.关于不定方程x3±27=py2[J].湖北民族学院学报:自然科学版 2013,31(2): 182-183.

[6] 李复中.关于丢番图方程x3±64=3Dy2[J].东北师范大学报:自然科学版,1994(2):16-17.

[7] 张海燕,李复中.关于丢番图方程x3±64=Dy2[J].哈尔滨科学技术大学学报,1994,18(3):107-109.

[8] 赵天.关于不定方程x3±23n=3Dy2解的讨论[D].重庆:重庆师范大学,2008:10-32.

[9] 张攀.关于不定方程x3±64=py2的研究[D].西安：西北大学,2012.