一类常微分方程边值问题的Green函数讨论

李君君

(南京财经大学 应用数学学院, 江苏 南京 210023)

0 引言

二阶常微分方程的通解中有两个任意常数,需要有两个条件才能确定它们,如果把两个条件都加在同一点上,就是初值问题．如果在一个区间的两个端点各加一个条件,这样的问题就叫做边值问题．对于常微分方程边值问题,我们可以将常微分方程转化为积分方程,从而可以更加方便的求出方程的解．在这一过程中,有个很重要的方法就是利用Green函数．比如,对于二阶非齐次常微分方程

p0(x)y″+p1(x)y′+p2(x)y=f(x)

的解即为

Green函数在常微分方程中的研究中有着重要的作用,利用它将原方程转化为积分方程,可以广泛应用于流体力学、振动理论、电子工程等学科中．显然,边值问题解的问题就转化为求常微分方程的Green函数的问题．那么,同样的,Green函数的唯一性也就确定了解的唯一性．所以求Green函数就是成为问题的关键．关于如何求Green函数,目前还没有统一的方法．不同的资料给出了很多方法,主要是通过求方程的朗斯基行列式,利用朗斯基行列式求其解,通过进一步的化简,找出Green函数,但这种方法计算较复杂,而且会因初值条件选择的不同,使得计算难度加大．

本文将研究二阶微分方程

L(y)=p0(x)y′′+p1(x)y′+p2(x)y=0

(1)

在一些边界条件下的Green函数．我们所用的这种待定系数法是一种常见而且简单的方法,大部分常微分方程边值问题的Green函数都可以用这种方法求出．

本文注重研究方程(1)在周期边界条件下的Green函数的表达式及解唯一性的判断,从而给出一般方法．

对于边界条件

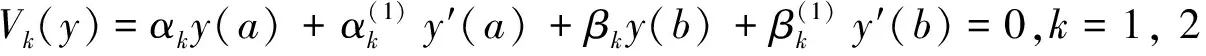
(2)

设上述y(a),y′(a),y(b),y′(b)的一次式V1,V2是线性独立的．

引理1[1]设ξ为(a,b)中的任意点:a<ξ

1) 在a≤x≤b上,G(x,ξ)本身连续;

3) 作为x的函数,G(x,ξ)在[a,ξ)及(ξ,b]是方程(1)的解L(G)=0;

4) 满足边界条件:Vk(G)=0,k=1, 2.

1 周期边界条件下的Green函数及证明.

首先设方程满足边界条件y(a)=y(b),y′(a)=y′(b).

定理1 方程(1)的Green函数为

其中y1(x),y2(x)是方程(1)的解．

证明设y1(x),y2(x)为方程的线性无关解,根据引理1的性质3),函数G(x,ξ)在区间[a,ξ)及(ξ,b]可由上述线性无关解表出,即可设

G(x,ξ)=a1y1(x)+a2y2(x),a≤x<ξ,G(x,ξ)=b1y1(x)+b2y2(x),ξ

式中a1,a2,b1,b2是ξ的函数．所以要求G(x,ξ)只要求出a1,a2,b1,b2即可．根据引理性质1),2)我们可以得到下列方程组

不妨令ck=bk-ak,k=1,2.则上述方程组可化简为

容易求出

(3)

接下来我们再根据边值条件y(a)=y(b),y′(a)=y′(b)及引理1的性质3)有

G(a,ξ)=G(b,ξ),G′(a,ξ)=G′(b,ξ),

即

又因为c1=b1-a1,c2=b2-a2,容易解出

所以方程(1)的格林函数为

其中c1,c2如(3)所求,证毕．

引理2[1]如果边值问题(1)(2)只有零解y(x)=0,则算子L有且只有一个Green函数．

在定理1的证明中,我们不难看出证明的过程给出的求解二阶线性常微分方程边值问题的Green函数的解法,也就是本文所介绍的待定系数法:

1) 求出方程的基本解组,再求出其通解．根据边值条件判断,是否只有零解,则再根据引理2,判断Green函数是否唯一;

2) 若Green函数唯一,根据引理1的性质3)构造Green函数;

3) 根据引理1的性质1)，2)构造方程组,再代入边值条件求出系数,从而解出Green函数．

例1 求边值问题

的Green函数．

解方程的基本解组为e-x,xe-x,通解为y=C1e-x+C2xe-x,其中C1,C2为任意常数．根据边值条件,有C1=C1e-1+C2e-1,-C1+C2=-C1e-1,得C1=C2=0,即方程仅有零解y(x)=0．根据引理,Green函数唯一．设Green函数为

G(x,ξ)=a1e-x+a2xe-x, 0≤x<ξ,G(x,ξ)=b1e-x+b2xe-x,ξ

由引理1的性质1),2)有

记c1=b1-a1,c2=b2-a2.

所以有

解得c1=ξeξ,c2=-eξ

又根据边值条件,有G(0,ξ)=G(1,ξ),G′(0,ξ)=G′(1,ξ)即

又有b1-a1=c1=ξeξ,b2-a2=c2=-eξ.

容易解得

所以方程的Green函数是

2 方程在另外几种边界条件下的Green函数

下面我们以定理的形式给出其他边值条件下的相应结论及其证明．

定理2 二阶边值问题

的Green函数为

证明设y1(x),y2(x)为方程的线性无关解,根据引理1的性质3),函数G(x,ξ)在区间[a,ξ)及(ξ,b]可由上述线性无关解表出,即可设

G(x,ξ)=a1y1(x)+a2y2(x),a≤x<ξ,G(x,ξ)=b1y1(x)+b2y2(x),ξ

式中a1,a2,b1,b2是ξ的函数．

根据引理1的性质1),2)我们可以得到下列方程组

不妨令ck=bk-ak,k=1,2.则上述方程组可化简为

容易求出

接下来我们再根据边值条件y(a)=y(b)=0及引理1的性质3)有G(a,ξ)=G(b,ξ)=0.

即

又因为c1=b1-a1,c2=b2-a2,容易解出

所以Green函数为

定理3 二阶边值问题

的Green函数为

证明设y1(x),y2(x)为方程的线性无关解,根据引理1的性质3),函数G(x,ξ)在区间[a,ξ)及(ξ,b]可由上述线性无关解表出,即可设

G(x,ξ)=a1y1(x)+a2y2(x),a≤x<ξ,G(x,ξ)=b1y1(x)+b2y2(x),ξ

式中a1,a2,b1,b2是ξ的函数．

根据引理1的性质1),2)我们可以得到下列方程组

不妨令ck=bk-ak,k=1,2.则上述方程组可化简为

容易求出

接下来我们再根据边值条件y(a)=y′(b)=0及引理1的性质3)有G(a,ξ)=G′(b,ξ)=0,

即

又因为c1=b1-a1,c2=b2-a2,容易解出

所以Green函数为

定理4 二阶边值问题

的Green函数为

证明设y1(x),y2(x)为方程的线性无关解,根据引理1的性质3),函数G(x,ξ)在区间[a,ξ)及(ξ,b]可由上述线性无关解表出,即可设

G(x,ξ)=a1y1(x)+a2y2(x),a≤x<ξ,

G(x,ξ)=b1y1(x)+b2y2(x),ξ

式中a1,a2,b1,b2是ξ的函数．

根据引理1的性质1),2)我们可以得到下列方程组

不妨令ck=bk-ak,k=1,2.则上述方程组可化简为

容易求出

接下来我们再根据边值条件y′(a)=y(b)=0及引理1的性质3)有G′(a,ξ)=G(b,ξ)=0,

即

又因为c1=b1-a1,c2=b2-a2,容易解出

所以Green函数为

定理5 二阶边值问题

的Green函数为

证明设y1(x),y2(x)为方程的线性无关解,根据引理1的性质3),函数G(x,ξ)在区间[a,ξ)及(ξ,b]可由上述线性无关解表出,即可设

G(x,ξ)=a1y1(x)+a2y2(x),a≤x<ξ,G(x,ξ)=b1y1(x)+b2y2(x),ξ

式中a1,a2,b1,b2是ξ的函数．

根据引理1的性质1),2)我们可以得到下列方程组

不妨令ck=bk-ak,k=1,2.则上述方程组可化简为

容易求出

接下来我们再根据边值条件y′(a)=y′(b)=0及引理1的性质3)有G′(a,ξ)=G′(b,ξ)=0,

即

又因为c1=b1-a1,c2=b2-a2,容易解出

所以Green函数为

在此,仅举其中一例加以说明．

的Green函数．

解由例1我们已经知道方程的基本解组为e-x,xe-x,通解为y=C1e-x+C2xe-x,其中C1,C2为任意常数且C1=C2=0,即方程仅有零解y(x)=0．根据引理,Green函数唯一．设Green函数为

G(x,ξ)=a1e-x+a2xe-x, 0≤x<ξ,G(x,ξ)=b1e-x+b2xe-x,ξ

根据例1的结果有

c1=ξeξ,c2=-eξ,

根据边值条件

G(0,ξ)=a1=0,G(1,ξ)=b1e-1+b2e-1=0,

所以

b1=c1+a1=ξeξ,b2=-ξeξ,a2=b2-c2=-ξeξ+eξ,

故Green函数为

G(x,ξ)=(-ξeξ+eξ)xe-x,0≤x<ξ,

G(x,ξ)=ξeξe-x-ξeξxe-x,ξ

参考文献：

[1] 沈以淡. 积分方程[M].北京:清华大学出版社,2012:272-274.

[2] 蔡燧林. 常微分方程[M].武汉:武汉大学出版社,2003:328-329.

[3] 葛渭高,李翠哲,王宏洲. 常微分方程与边值问题[M].北京:科学出版社,2008:172-174.

[4] 刘丽环,常晶,高艳超. 二阶常微分方程边值问题的格林函数求法[J].长春工业大学学报,2011,32(1):102-104.

[5] 赵增勤.一类常微分方程边值问题的格林函数求法[D].山东:曲阜师范大学,2009.

[6] Po Fang Hsieh, Yasutaka Sibuya. Basic Theory of Ordinary Differential Equations[M].New York:Springer-Verlag,1999:148-150.

[7] Pokornyi Yu V ,Borovskikh A V. The connection of the green’s function and the influence function for nonclassical problems[J].Journal of Mathematical Sciences,2004,119(6):739-768.