算子Dn+p-1在亚纯p叶星象函数上的应用

袁 媛, 杨恋波

(马鞍山师范高等专科学校, 安徽 马鞍山 243041)

0 引言

定义函数

用f1(z)和f2(z)表示Hadamard乘积(或卷积)

定义函数

其中(x)k是Pochhammer符号．

记

φp(n+p,1;z)=z-p2F1(1,n+p;1;z),

对应函数φp(n+p,1;z),用Hadamard乘积为f(z)∈∑p定义一个新的线性算子Dn+p-1:

Dn+p-1f(z)=φp(n+p,1;z)*f(z).

对于函数f(z)∈∑p,定义积分算子Jv,p

进一步,定义函数H(z)

H(z)=(1-λ(n+2p+1))Dn+p-1f(z)+λ(n+p)Dn+pf(z)

(1)

其中f∈∑p,λ>0,n是大于-p的任意整数．

令f(z)和F(z)在开单位圆盘E={z:|z|<1}上解析,称函数f(z)从属于F(z),记为f(z)F(z),若F(z)是单叶的,f(0)=F(0)且f(E)⊂F(E).

1 主要结论

下面将讨论线性算子Dn+p-1定义在亚纯p叶函数上的一些应用．

引理1 若f(z)∈∑p,则

z(Dn+p-1f(z))′=(n+p)Dn+pf(z)-(n+2p)Dn+p-1f(z)

(2)

其中n是大于-p的任意整数．

引理2[1]令Ω是复平面C上的一个集合,b是一个满足Reb>0的复数．假设函数ψ:C2×E→C满足条件

ψ(ix,y;z)∉Ω

(3)

其中所有的实数x,y≤-|b-ix|2/(2Reb)且所有的z∈E．若函数p(z)满足p(z)=b+a1z+a2z2+…在E上解析且ψ(p(z),zp′(z);z)∈Ω,则在E上Rep(z)>0.

引理3[1]令h(z)在U={z:z∈C且|z|<1}上是凸单叶的,h(0)=1且令g(z)=1+b1z+…在U上解析．若g(z)+zg′(z)h(z), 则g(z)

引理4[3,5]令函数p(z)=1+c1z+…在U上解析且p(z)≠0(z∈U).若存在一点z0∈U使得

|argp(z)|<πγ/2,(|z|<|z0|) 且|argp(z0)|=πγ/2,(0<γ≤1).

则我们有z0p′(z0)/p(z0)=ikγ,其中

且(p(z0))1/γ=±i(n+p),n是大于-p的任意整数线性算子Dn+p-1具有以下性质[2],[6]:

定理1 令λ,α是实数且λ≥0,α>1,n是大于-p的任意整数．设g(z)∈∑p满足

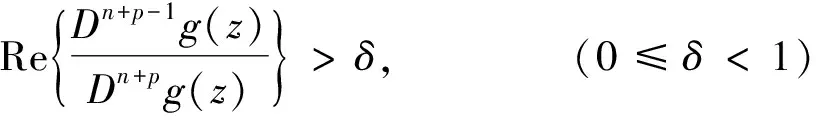
(4)

若f(z)∈∑p满足

(5)

则有

(6)

根据上述定理,立即能得到下面的结论．

推论1 令λ,α是实数且λ≥1,α>1,n是大于-p的任意整数．设g(z)∈∑p满足条件(4).若f(z)∈∑p满足(5),则

将n+p=a和1=c代入上述定理,有

推论2 令λ,α,a是实数且λ≥1,α>1,a>0.设g(z)∈∑p满足

则

将n+p=v代入上述定理,得到

推论3 令λ,α,v是实数且λ≥1,α>1,v>0.设g(z)∈∑p满足

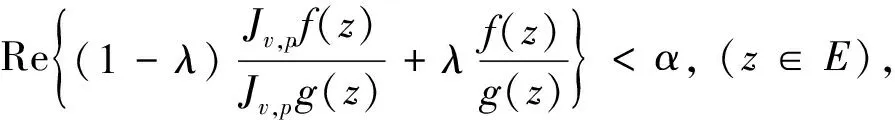
定理2 令f∈∑p且设H(z)是由式(1)定义的．若

(7)

则

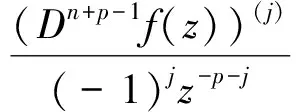
(8)

其中j∈N∪{0},λ>0,|B|≤1且A≠B.

证明由引理1和(1),得

H(j)(z)=(1-λ(n+2p+1))(Dn+p-1f(z))(j)+λ(n+p)(Dn+pf(z))(j)=

(1-λ+λj)(Dn+p-1f(z))(j)+λz(Dn+p-1f(z))(j+1)

(9)

代入

(10)

其中f∈∑p,我们发现g(z)=1+b1z+…在U上解析．由于

(11)

由于h(z)=(1+Az)/(1+Bz)是在U上是凸单叶的,应用引理1推出

g(z)

式(8)得证．

定理3 令f∈∑p且设H(z)是由式(1)定义的．若

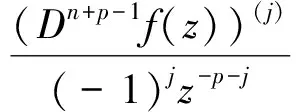
(12)

则

(13)

其中j∈N∪{0},0≤α<1,0<λ<1/(p+1)且

(14)

这里ρ是精确的．

证明代入

其中对0<λ<1/(p+1),β=λ/(1-λ-λp)>0.

现在表示

(15)

其中ρ=(1+β2)1/2-β且0<ρ<1.

其中由(15)给出的|z|=r<ρ.故函数φ满足积分式

(16)

其中μ(x)是|x|=1上的一个概率测度．

Reg(z)>α, (0≤α<1;z∈U)

(17)

(18)

因此,由定理2中的(11)和(18),可以得到(13)的结论．

为了显示界限ρ是精确的,我们代入下列定义中的f∈∑p

得到

其中z=ρeiπ. 证毕．

参考文献：

[1] Miller S S, Mocanu P T. Differential subordination and univalent functions[J]. Michigan Math, 1981,28:157-171.

[2] Miller S S, Mocanu P T. On some classes of first order differential subordination[J].Michigan Math,1985,32:185-195.

[3] M.Nunokawa. On properties of non-caratheodory functions[J]. Proc Jpn Acad Ser A:Math Sci, 1992,68:152-153.

[4] Aouf M K, Hossen H M. New criteria for meromorphic p-valent starlike functions[J].Tsukuba J Math, 1993,17:481-486.

[5] Nunokawa M. Some results for strongly starlike functions[J]. Math Anal Appl,1997,212:98-106.

[6] Liu J L,Srivastava H M. A linear operator and associated families of meromorphically multivalent functions[J]. Math Anal Appl, 2001, 259:566-581.