分类讨论解题策略
郭培俊, 郭晓曼
(1.浙江工贸职业技术学院, 浙江 温州 325003; 2.中南民族大学 经济学院, 湖北 武汉 430074)
1 分类讨论概述
分类与讨论是一种重要的数学思想,也是一种数学能力[1].当面临的问题不宜用一种方法处理或同一种形式叙述时,就把问题按照一定的原则或标准分为若干类,然后逐类进行讨论,再把这几类的结论汇总,得出问题的答案,这种解决问题的思想方法就是分类讨论的思想方法.
当我们所研究的各种对象之间过于复杂或涉及范围比较广泛时,我们大多采取分类讨论的方法进行解决,即对问题中的各种情况进行分类,或对所涉及的范围进行分割,然后分别研究和求解.分类讨论解题的实质,是将整体问题化为部分问题来解决,以增加题设条件[2].
分类讨论的思想方法的实质是把问题“分而治之,各个击破”.其一般规则及步骤是:(1)确定同一分类标准;(2)恰当地对全体对象进行分类,按照标准对分类做到“既不重复又不遗漏”;(3)逐类讨论,按一定的层次讨论,逐级进行;(4)综合概括小结,归纳得出结论[3].
分类讨论,一方面可将复杂的问题分解成若干个简单的问题,另一方面恰当的分类可避免丢值漏解,从而提高全面考虑问题的能力,提高周密严谨的数学素养.
近年来,在各地专升本试题中涉及“分类讨论”的问题越来越显现,因为这类试题不仅考查学生的数学基本知识与方法,而且考查了学生思维的深刻性.在解决此类问题时,因考虑不周全导致失分的较多,究其原因主要是平时的学习中,由于高职生学习数学时间少和高职学习数学的要求“扁平化(必须、够用原则)”,导致对“分类讨论”的数学思想渗透不够,个人水平偏低.这需要参加专升本的学生补上一课,花点时间加强“分类讨论”的学习.
应用分类讨论思想解决问题必须保证分类科学,标准统一,做到不重复,不遗漏,并力求最简、完备.
2 分类讨论常见知识点
分类讨论是解题的需要,是同一本质的几种表现形式,是准确反映事物本质的要求.在专升本《高等数学》中,分类讨论常见的知识点有:
指数函数y=ax,其中底数a是参数,要分为0
对数函数y=logax,底数a是参数,要分为0
分段函数在分界点处的极限、导数要分左右极限、导数讨论;
x→∞的极限往往要分为x→+∞,x→-∞两情况讨论;

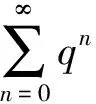
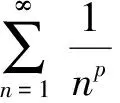
对函数的零点、驻点、极值点、拐点往往也作为讨论的对象,主要考察这些点把定义域分成的各个不同区间内所分析函数的性质.
3 分类讨论的例题解析
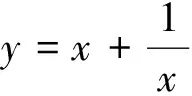
分析 把定义域按可能取得极值的极值点进行分类 ,即用驻点和不可导点将定义域分成不同的区间.
解函数的定义域为{x|x≠0}.
令y′=0得驻点x=-1,x=1.不可导点为x=0.
三个点x=0,x=-1,x=1把定义域分成四段,列表如下:
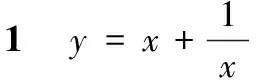
表的单调区间
所以单调递增区间为(-∞,-1),(1,+∞);单调递减区间为(-1,0),(0,1).
例2试确定函数y=|x(1-x)|的单调性与极值[4].
分析 同例1一样,按可能取得极值的极值点进行分类 (用驻点和不可导点将定义域分成区间),而不可导点往往在分段函数的分界点处.本题在对含绝对值函数进行分段的基础上,再用驻点进行二次分类.
解显然y=y(x)是一个分段函数
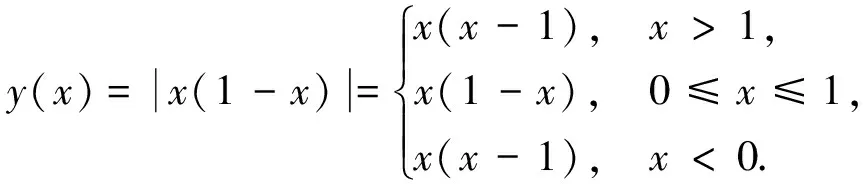
由导数定义得y(x)在x=0处的左、右导数分别为
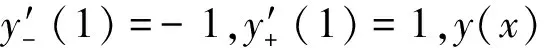
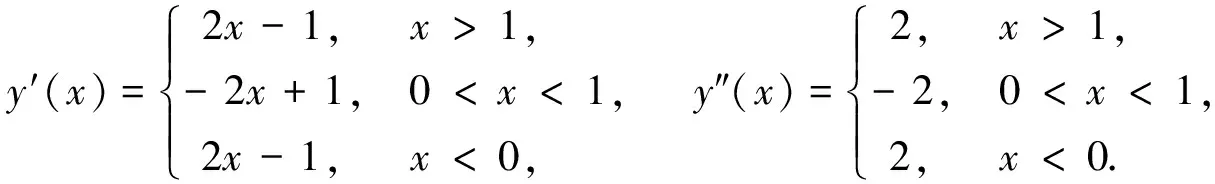
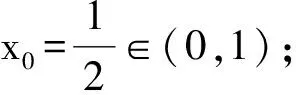

表2 函数y=|x(1-x)|的单调区间
例3讨论曲线y=4lnx+k与y=4x+ln4x的交点个数.
分析 问题等价于讨论方程ln4x-4lnx+4x-k=0有几个不同的实根.除了对x进行分类讨论外,还要对参数k进行分类讨论.
解设φ(x)=ln4x-4lnx+4x-k,则
令φ′(x)=0,得唯一驻点x=1.
当0
当φ(1)>0,即当k<4时,φ(x)≥φ(1)>0,φ(x)无零点.
当φ(1)=0,即当k=4时,φ(x)≥φ(1)=0,φ(x)有唯一零点.
当φ(1)<0,即当k>4时,由于
故φ(x)有两个不同的交点.
综上所述,当k<4时,两曲线没有交点;当k=4时,两曲线仅有一个交点;当k>4时,两曲线有两个交点.
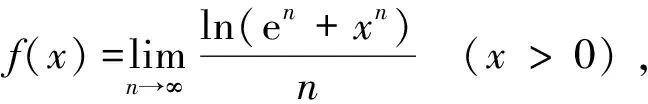
分析 通过观察,需对en,xn进行大小比较,转化为e,x的比较.分三种情况:x
解(i)当x (ii)x=e时, (iii)x>e时, 分析 分段函数有一个分界点,求导要分类.本题要分为x<0,x>0,x=0三种情况.特别注意不能忽视第三种情况,即如何求f′(0). 解(i)x<0时,f′(x)=-2e2x. (ii)x>0时,f′(x)=2x. (iii)x=0时,由于f(0)=0,而 例6设f(x)在(-∞,+∞)内连续,且对x,y的一切实数值满足 f(x+y)=f(x)+f(y), 试证f(x)在(-∞,+∞)内为线性函数f(x)=ax,其中a=f(1). 分析 首先进行一级分类,把实数分为有理数和无理数,只须对有理数进行分析,无理数用极限逼近成有理数情况;再进行二级分类,把有理数又可分成整数、分数(分子为1或不为1)进行讨论.最后采用从特殊到一般的思想进行归纳推理.分类结构为 证任取x∈(-∞,+∞),当y=0时,由题设可知 f(x)=f(x+0)=f(x)+f(0), 由此可得f(0)=0.若取y=-x,则由题设可知 f(0)=f(x-x)=f(x)+f(-x)=0, 从而知f(-x)=-f(x).即f(x)为奇函数. 对x进行分类讨论 1. (x取整数)设x=k,k为正整数,由数学归纳法可证得 f(k)=f(1+1+…+1)=kf(1). 从而 综上可知,任取x为有理数,总有f(x)=f(1)x. 综上可知,在(-∞,+∞)内,恒有f(x)=f(1)x=ax,其中a=f(1). 分析 以0为分界点,对k分三种情况讨论. 对k分以下三种情况讨论: (i) 当k>0时,由上式得 (ii)当k=0时,原级数的通项un=1不趋于零,故原级数发散. (iii) 当k<0时, -k>0,原级数的通项un=(ln(1+n))-k趋于+∞,故原级数发散. 综上,原级数发散. 例8求微分方程y″-ay=0的通解,其中a为常数. 分析 在特征方程中,对a分三种情况讨论. 解这是常系数线性齐次微分方程,它的特征方程为r2-a=0. 当a=0时, 特征根r=0是二重根,原方程的通解为 y=C1+C2x. (A)连续点 (B)可去间断点 (C)跳跃间断点 (D)第二类间断点 提示 通过讨论x→0-,x→0+的左、右极限再作判断. (vi) 设函数f(x)的定义域是0≤x≤1,求g(x)=f(x+a)+f(x-a)的定义域,其中a>0为常数. (vii) 设函数 试求复合函数f[g(x)]与g[f(x)]. (viii) 设f(x)在[0,1]上连续,且f(0)=f(1)=0,试证对任意一个实数l(0 (x) 试确定实常数a,b的不同取值范围,讨论方程ax=bx,a>1的实根分布. [参 考 文 献] [1] 王镇海.关于数学分类讨论题的教学[J].教学与管理,1992,9(3):43-44. [2] 张小芳.浅谈教学应如何进行分类讨论[J].成功(教育),2010,4(2):114-115. [3] 王勇.分而治之,各个击破——解读分类讨论的思想方法[J].高考(数语英),2007,3(Z1):29—30. [4] 邵剑,李大侃.高等数学专题梳理与解读[M].上海:同济大学出版社,2008. [5] 毛纲源.考研数学(二)常考题型及其解题方法技巧归纳[M]武汉:华中科技大学出版,2004.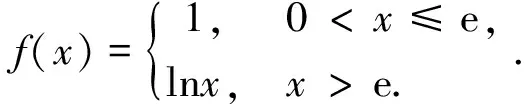
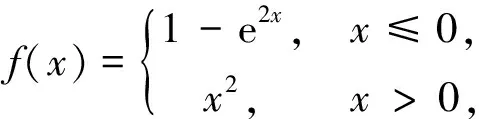
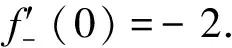
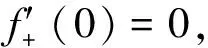

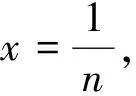
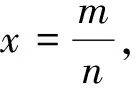




4 分类讨论练习