关于无穷小比较的一点注记

顾艳红， 赵玉英

(北京林业大学 理学院，北京 100083)

1 引 言

无穷小是极限为零的变量，作为数学分析和高等数学中的一个重要概念，它却又有几分神秘，给人一种不可捉摸之感.因此有人把它比喻成田野上远处的地平线，看得见，却又走不到它跟前.正是其神秘和复杂，触动了学者们的感情，也很少有别的观念像无穷那样激励理智产生富有成果的思想[1].

在数学分析和高等数学的教学和研究中，很多学者也非常关注无穷小这一重要概念，尤其是对于无穷小的比较，从对其定义的科学性到教学内容与教学方法的设计[1-6]，他们都进行了深入探索和讨论，揭示出无穷小的神秘一面.

对于两个无穷小，如果α是比β高阶的无穷小量，未必等价于β是比α低阶的无穷小量[1-3]；对于任何两个无穷小量，并非都可以进行阶的比较[6].在文[6]中还给出了确定无穷小量阶的定理.在此基础上，本文进一步说明，对于两个非0的无穷小α与β，即使在能比较阶的高低情况下，α未必是β的k(k>0)阶无穷小.

2 无穷小比较的定义

关于两个无穷小的比较，文[7]给出了如下定义.

定义1[7]设在自变量的同一变化过程中，α与β为无穷小，且α≠0，

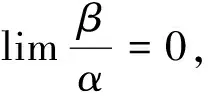
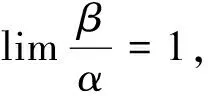
3 关于无穷小比较的一点注记及例子

在文[1]和文[2]的基础上，本文给出关于无穷小比较的一点注记.

注 两个非0无穷小即使在能比较阶的高低情况下，一个无穷小未必是另一个无穷小的k(k>0)阶无穷小.

当x→0时，0是其它非0无穷小的高阶无穷小，但0不是其它非0无穷小的k(k>0)阶无穷小.对于两个非0无穷小，构造出了如下两个例子.

证根据洛必达法则[7]，

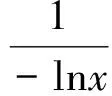
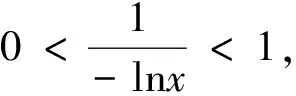
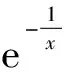
证

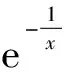
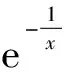
根据洛必达法则，

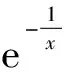
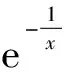
4 结束语

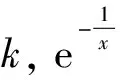
表的取值对照

[参 考 文 献]

[1] 方涛.关于无穷小量的几点注记[J].上海工程技术大学学报,2013,27(3):275-277.

[2] 龚冬保.高阶无穷小与低阶无穷小:无穷小比较的一个问题[J].高等数学研究，2000，3(3):16.

[3] 潘建辉，胡学刚，邓志颖.关于“无穷小的比较”的教学研究[J].高等数学研究，2011，14(5):43-46.

[4] 马怀远.再谈无穷小比较的解释[J].江苏教育学院学报(自然科学)，2012，28(4):16-17,63.

[5] 潘建辉,邓志颖,杨春德.“无穷小的比较”的定义及其改进[J].大学数学,2011,27(3):204-208.

[6] 邓俊兰.关于无穷小量阶的若干注记[J].南阳师范学院学报，2010，9(9):81-83.

[7] 同济大学数学系编.高等数学(上册)[M].6版.北京.高等教育出版社，2007：57-59.