若干数学竞赛试题的统一解法

潘 杰， 苏化明

(合肥工业大学 数学学院，合肥 230009)

首先介绍几道关于定积分计算的数学竞赛试题.

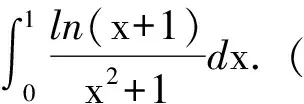
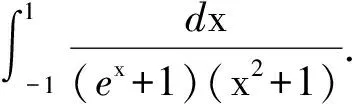
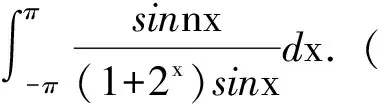
本文将给出一个关于定积分的命题，由此命题可以给出以上几道试题的统一解答，然后再通过另外的实例进一步说明此命题的应用.

命题设f(x)，g(x)为[a,b] (b>a)上的连续函数. 若f(x)=f(a+b-x)，g(x)+g(a+b-x)=m(常数)，则有

(1)

证令x=a+b-t，则

于是

由于f(a+b-x)=f(x)，所以

试题(A)的解答.

故由(1)可得

试题(B)的解答.

故由(1)可得

试题(C)的解答.

令x=tant，则有

故由(1)可得

注 本试题还有其他解法.

试题(D)的解答.

试题(E)的解答.

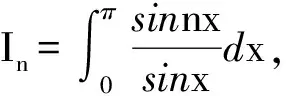
故In=In-2(n=2,3,…).

由于I0=0，I1=π,所以

试题(F)的解答.

故由(1)可得

因此

下面再举几个例子进一步说明本文所给命题在某些积分计算中的应用.

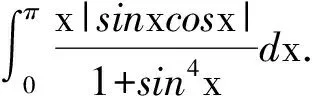
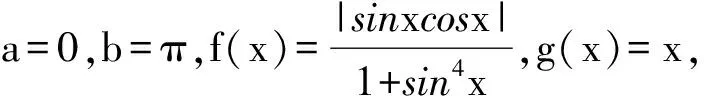
由于

令x=π-t，则

故

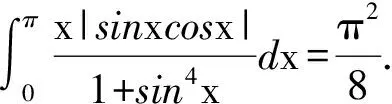
解在(1)中取a=0，b=nπ，f(x)=|sinnx|，g(x)=x，则有f(nπ-x)=f(x)，g(nπ-x)=nπ-x，g(x)+g(nπ-x)=nπ，故由(1)可得

由于

因此所求积分I=n2π.

例3[6]证明：

并求I的值. (陕西省第八次大学生高等数学竞赛试题，2010年)

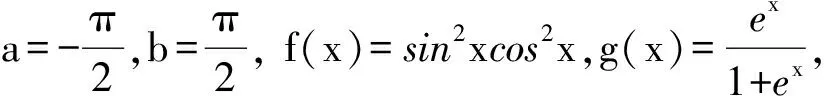
因此

[参 考 文 献]

[1] 刘培杰数学工作室组织编译.历届PTN美国大学生数学竞赛试题集(1938—2007)[M].哈尔滨：哈尔滨工业大学出版社，2009.

[2] 许康，陈强，陈挚，陈娟编译.前苏联大学生数学奥林匹克竞赛题解(下编)[M].哈尔滨：哈尔滨工业大学出版社，2012.

[3] 王丽萍编译.历届IMC国际大学生数学竞赛试题集(1994—2010)[M].哈尔滨：哈尔滨工业大学出版社，2012.

[4] 李心灿，季文铎，孙洪祥，邵鸿飞，吴纪桃，张后扬.大学生数学竞赛试题解析选编[M].北京：机械工业出版社，2011.

[5] 李重华，孙薇荣，景继良，郑麒海.上海交通大学1982—1995年高等数学竞赛试题精解[M].上海：上海科学普及出版社，1996.

[6] 陕西省第八次大学生高等数学竞赛试题[J].高等数学研究，2010，13(6)：64-65.