Taylor公式中的Lagrange型余项Rn(x)的探讨

丁殿坤， 边平勇

(山东科技大学 基础课部， 山东 泰安 271019)

1 引 言

Taylor中值定理是高等数学(数学分析)的重要内容之一，也是Lagrange中值定理的推广，它可以把一个函数f(x)展为

当x0=0时，

根据精确程度要求来计算函数在x0(或x=0)附近的函数值，误差不超过|Rn(x)|，其中

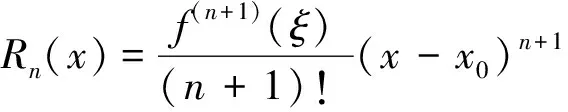
但高等数学(数学分析)教材中通常都是把sinx，cosx分别展成

和

其中

那么，就提出这样一个问题：对于缺项的Taylor公式，其余项Rn(x)是用

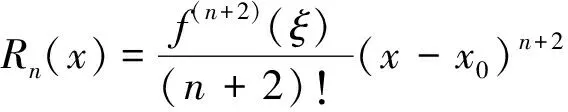
表示的，能否用

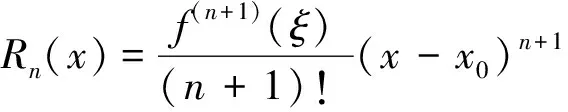
来表示呢？下面就这个问题进行探讨.

2 定理与推论

上面的问题归结为：是否存在ξ0(或θ0)使

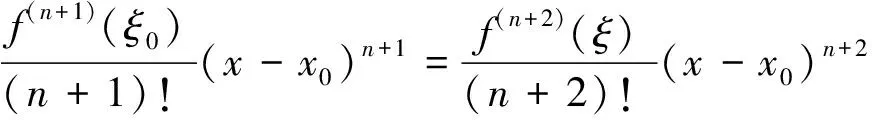
于是给出如下定理.

定理设f(x)在含x0的某区间内有直到(n+2)阶导数，若f(n+1)(x0)=0，则存在ξ0和ξ使f(x)的Taylor公式的余项

成立.

证在以x,x0为端点的区间上将f(n+1)(x)应用Lagrange中值定理便得

f(n+1)(x)-f(n+1)(x0)=f(n+2)(ξ)(x-x0).

而f(n+1)(x0)=0，所以，

f(n+1)(x)=f(n+2)(ξ)(x-x0)，

(1)

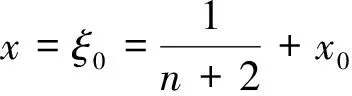
(2)

(3)

由(2)式和(3)式得

于是当x0=0时可得到如下推论：

推论设f(x)在含有x=0的某区间内有直到(n+2)阶导数. 若f(n+1)(0)=0，则一定存在0<θ0<1和0<θ<1使f(x)的Maclaurin公式的余项

成立.

定理和推论就回答了上面提出的问题，所以sinx，cosx亦可分别写成

和

其中

[参 考 文 献]

[1] 同济大学应用数学系.高等数学(上册)[M]. 5版. 北京：高等教育出版社，2002：137-143.

[2] 陈纪修，於崇华，金路. 数学分析(上册)[M]. 北京：高等教育出版社，2000：194-204.

[3] 王绵森，马知思. 工科数学分析基础(上册)[M]. 北京：高等教育出版社，1998：138-142.

[4] 王志平.高等数学大讲堂[M]. 大连：大连理工大学出版社，2004：108-110.