J正交矩阵的一些性质

袁志杰

(合肥工业大学数学学院，合肥230009)

1 引 言

称对角元为+1或-1的n阶对角矩阵为符号矩阵，记为J.

定义若存在n阶符号矩阵J，使得QJQT=J，则称n阶矩阵Q为J正交矩阵，或称为超正规矩阵.

2 主要结论

关于J正交矩阵，下列性质是显然的：

性质1若Q为J正交矩阵，则JQ,QJ,JQJ也是J正交矩阵.

性质2若Q为J正交矩阵，则Q非奇异，且Q-1=JQTJ.

性质4若Q为J正交矩阵，则detQ=1.

性质5若Q为J正交矩阵，则Q-1,Qn也是J正交矩阵.

性质1与性质2只需注意到J2=I即可得，性质3首先证明QT也是J正交矩阵，顺便纠正文献[1]的笔误(P149-P150).在QJQT=J的两边同时右乘JQ得

QJQT(JQ)=J(JQ)， 即QJ(QTJQ)=Q.

在该式两边同时左乘J-1Q-1，可得QTJQ=J-1=J，即QT也是J正交矩阵.至于后面的分块矩阵，根据定义可证也是J正交矩阵(不同的是符号矩阵).对QJQT=J两边同取行列式便得性质4.根据性质2和性质3，Q-1是J正交矩阵；而

QnJ(Qn)T=Qn-1(QJQT)(Qn-1)T=Qn-1J(Qn-1)T=…=QJQT=J，

故Qn也是J正交矩阵.

下面的定理给出了J正交矩阵的F范数的估计，即定理1.

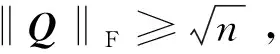
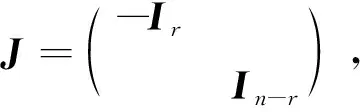
(1)

故

从而

Q是正交矩阵；反之显然.

推论1设Q是对称的J正交矩阵，则有

其中S=iJ的第i个对角元为-1.

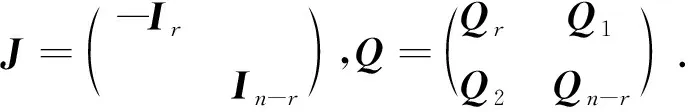
其中S=iJ的第i个对角元为-1.

正交矩阵的特征值的模必为1，但J正交矩阵是否还具有该性质呢？设λ是J正交矩阵Q的一个特征值，x是属于λ的特征向量，即Qx=λx，由于QTJQ=J，在该式两边同时左乘xT和右乘x，得xTQTJQx=xTJx，即λ2xTJx=xTJx，因为xTJx未必非零，故λ2=1未必成立，下面的定理给出了特征值的模为1的充分条件.

定理2若λ是n阶J正交矩阵Q的k重特征根，且k>n-k，则|λ|=1.

证首先由于Q-1=JQTJ，故Q-1与Q有相同的特征值.设Q的特征值为

(2)

其中

λ≠μi(i=1,…,n-k)，

则Q-1的特征值为

(3)

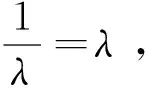
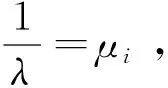
(4)

由于(3)与 (4)为同一组数，可得

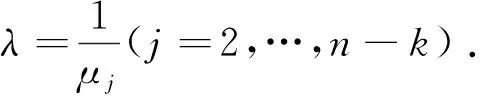
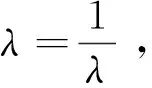
推论2若λ是n阶J正交矩阵Q的n重特征根，则必有λ=1.

证因为重特征根之积的模必为1，而所有特征根之积的模为1，故结论成立.

对于对称的J正交矩阵，关于特征根的结论还有下面的定理3.

定理3设Q为n阶对称J正交矩阵，且J≠I，则JQ必有特征根1与-1.

证当Q=J时，结论显然成立.假设Q≠J，由QJQ=J得(QJ)2=I，故QJ的特征根为1或-1.又存在正交阵R，使得

这里tii是QJ的特征根.若tii=1(i=1,…,n)，则由

可推知tij=0(i

推论3对于n阶对称J正交矩阵Q=(qij)n×n，当J≠I时，有

其中S=iJ的第i个对角元为-1.

由推论3的证明过程，可以得到2阶与3阶对称J正交矩阵Q的对角元之间的等式，即推论4.

推论4设J≠I.若Q为2阶对称J正交矩阵，则q11=q22；若Q为3阶对称J正交矩阵，则q11-q22-q33=1.

[参 考 文 献]

[1] 张贤达.矩阵分析与应用[M].北京：清华大学出版社，2004.

[2] 袁晖坪.准正交矩阵与准对称矩阵[J].工程数学学报,2004，21(4)：641-644.

[3] 佟文延.广义正交矩阵[J].数学学报,1984，27(6)：801.