一种组合数矩阵及其性质
丁 勇
(南京医科大学数学与计算机教研室,南京210029)
特殊的矩阵都有一些有趣的性质,这些矩阵在不同场合被用来作为典型的例子进行分析,说明相关的问题,例如范德蒙矩阵[1],Hilbert矩阵[2]等.
本文发现了一个与组合数有关的对称正定矩阵,该矩阵有一些有趣的性质,下面进行讨论.
1 组合数矩阵
设j-1为非负整数,用aij表示和为j-1的i≥1个非负整数所有取值的组合数,例如a33=6表示和为2的3个非负整数所有取值的组合有6种:
(2,0,0), (1,1,0), (1,0,1), (0,2,0), (0,1,1), (0,0,2).
将aij组成如下方阵
(1)
则上述矩阵有如下的规律性:第1行的元素全为1,其余行的第j个元素恰为上一行前j个元素的和,即
(2)
命题1满足(2)式的矩阵An的元素aij是和为j-1的i个非负整数所有取值的组合数.
证显然,和为定值j-1(j=1,2,…,n)的1个非负整数取值的组合只有一种,即只能取该值,故a1j=1,从而第1行的元素全为1.
和为定值j-1的2个非负整数取值,第一个数可取k(0≤k≤j-1),当第一个数确定后,第二个数也随之确定,即为j-1-k,故有j种组合,从而
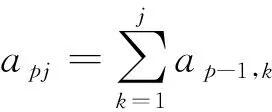

引理[3]设整数m≥1,则
(3)
命题2满足(2)式的矩阵An的元素为
(4)
证已知
归纳假设
由(2),(3)可得
现在aij又可理解为从j+i-2个不同元素中取出i-1个元素的组合数,与前面的和为非负整数j-1的i个非负整数所有取值的组合数之间有何联系?下面以j=4,i=3进行比较,进一步认清两者联系(表1).

表1 aij=a33的两种组合数的联系
表1左边为和为3的3个非负整数所有取值的组合,右边为从5个元素abcde中取3个的组合. 比较表1可发现,左边和右边两者联系可以这样理解:第一个数为从开始连续取元素的个数,第二个数为第一次取后隔一个再连续取剩余元素的个数,第三个数为第二次取后隔一个再连续取剩余元素的个数.
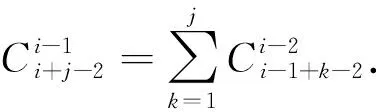
(5)
由以上讨论可知,矩阵(1)的元素与组合数有关,故不妨称其为组合数矩阵.
由公式(2)不难写出
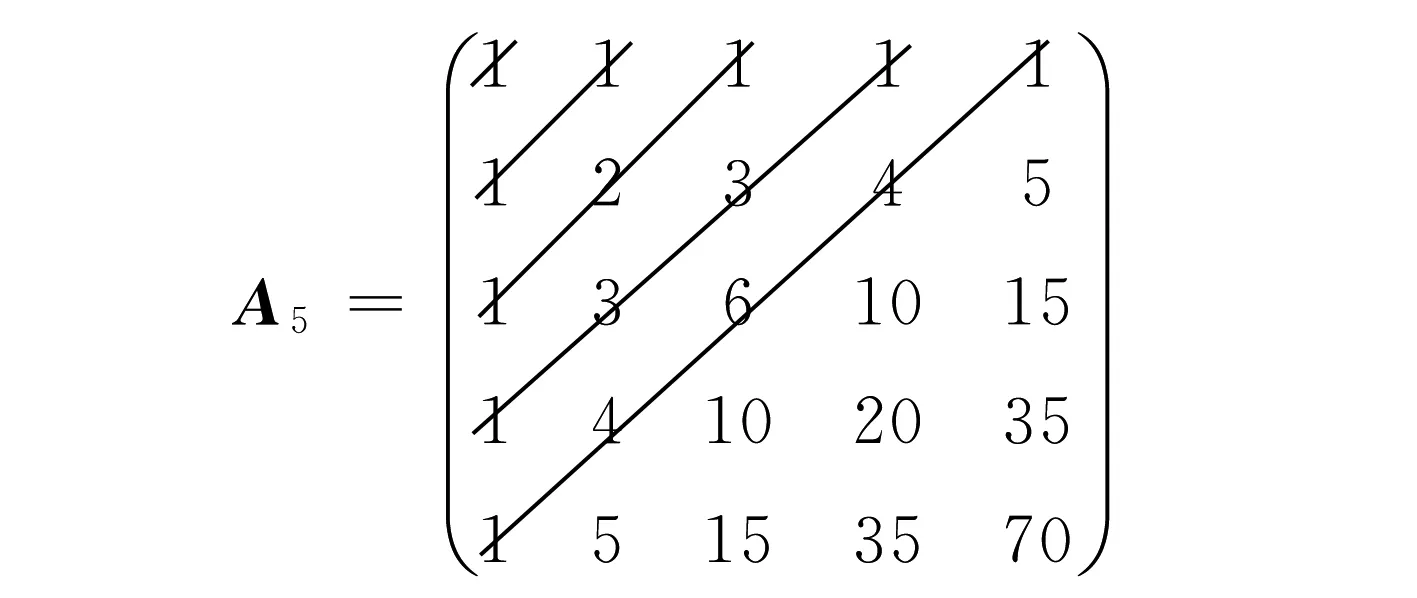
图1 5阶组合数矩阵与斜行元素示意图
2 组合数矩阵的性质
定义从i=1开始,下标之和i+j=k+1的元素aij称为第k斜行的元素.
例如,a11为第1斜行的元素,a12和a21称为第2斜行的元素,a13,a22和a31称为第3斜行的元素,….斜行元素示意图见图1.
关于An的元素有如下性质.
性质1(i)aij=aji(对称性);
(ii)aij=ai,j-1+ai-1,j(i,j≥2),
(6)
即当i,j≥2,An的任一元素为左边元素和上边元素之和;




(ii)由(2)可得
(iii)由(6)及对称性可得ann=an,n-1+an-1,n=2an,n-1为偶数,由(2)及对称性可得
(iv)由(4)可知
(v)由(4)可知



证(i) 记An的顺序主子式为
显然|A1|=|1|=1. 归纳假设|Ak|=1,由(6)可知
ai+1,j-aij=ai+1,j-1,ai,j+1-aij=ai-1,j+1,
从而依次将
第i行(i=k+1,k,…,2)减去第i-1行,可得
再依次将第i列(i=k+1,k,…,2),减去第i-1列,可得
从而

(ii)由性质1的(i)可知对称性,再由性质2的(i)及线性代数知识可知(ii)成立.
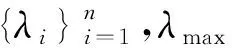
性质3(i)An的特征值都大于0,An的特征值之和为奇数;
(ii) 当n>1时,
证(i)由An的正定性可知其特征值都大于0,因为矩阵的特征值之和为对角线元素之和,由a11=1和性质1的(iii)可得证.
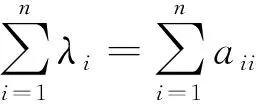
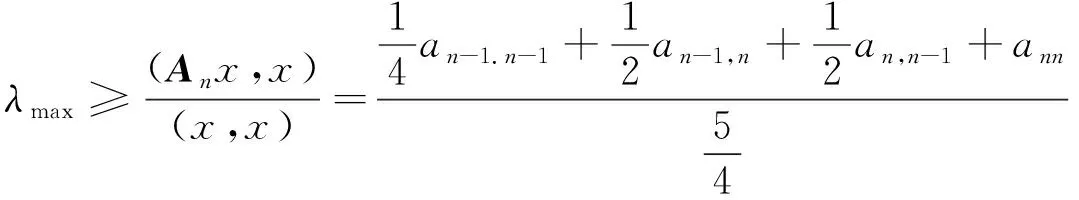
3 猜 想
组合数矩阵An,除了上述的性质外,通过数值计算,还发现其特征值可能还有如下有趣的性质,由于尚未证明,因此是猜想.表2是部分数据的结果.
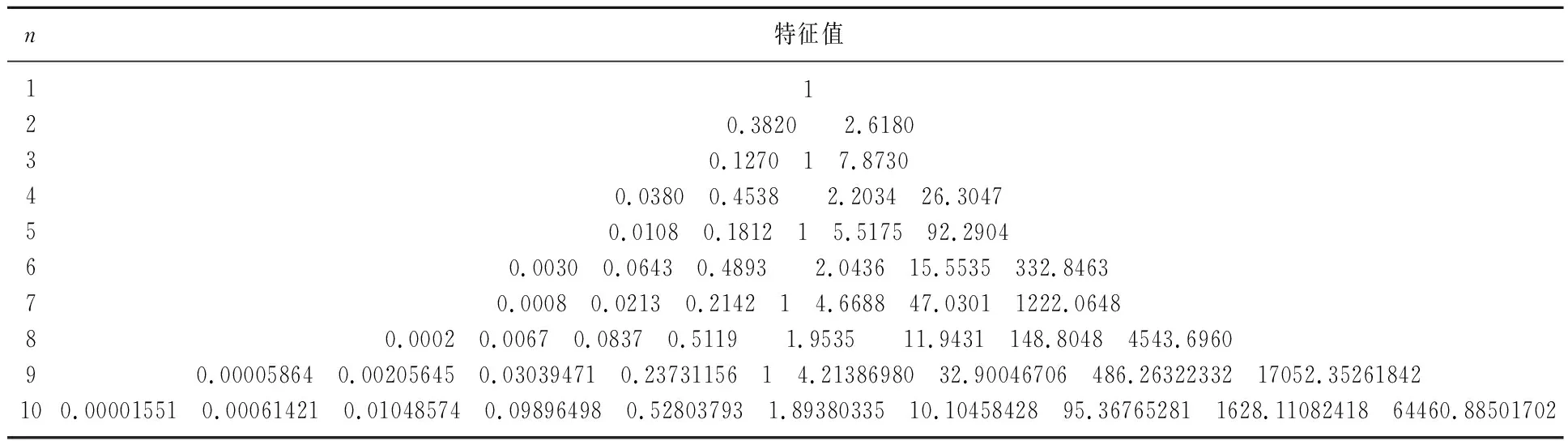
表2 组合数矩阵An (1≤n≤10)的特征值
(i)An有n个不同的特征值.当n为奇数时,An有一个特征值为1,其余特征值两两配对乘积为1;当n为偶数时,特征值两两配对乘积为1;
例如,n=2时,
(ii)An与其逆矩阵有相同的特征值;
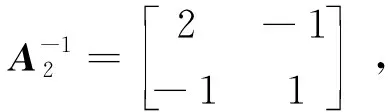
(iii)Ak+1的特征值分散在Ak的特征值两边;

[参 考 文 献]
[1] 叶彩儿. 范德蒙行列式的新证明及其应用[J]. 大学数学, 2011, 27(6) : 135-139.
[2] 李庆扬,王能超,易大义. 数值分析[M]. 5版. 北京:清华大学出版社,2008.
[3] 简明数学手册编写组. 简明数学手册[M]. 上海:上海教育出版社,1977:3-197.
[4] 吴世熙. 排列与组合[M]. 南京:江苏人民出版社, 1979:60.
[5] 浙江大学数学系高等数学教研组. 概率论与数理统计[M]. 北京:人民教育出版社,1979:42-43.
[6] 丘维声. 简明线性代数[M]. 北京:北京大学出版社, 2002.

