基于极值理论的空中加油软管风险定量评估

王良, 董新民, 王海涛, 程建锋

(空军工程大学 航空航天工程学院, 陕西 西安 710038)

0 引言

空中加油机的出现,使现代战争实现了“全球到达”、“全球打击”的能力,大大增强了世界各国的军事力量。空中加油过程由4个阶段组成:编队、对接、加油和脱开[1]。在对接阶段,若对加油机软管控制不当,则会使软管发生抽鞭现象而导致加油机软管断裂事故的发生。因此,对空中加油软管进行风险定量评估迫在眉睫。

目前,国内外针对空中加油软管风险分析研究还在初步阶段。文献[2-3]建立了空中加油软管锥套动力学模型,分析了大气紊流对软管锥套运动的影响;文献[4]根据碰撞接触算法和瞬态冲击理论建立了碰撞力模型,研究了对接时碰撞对加油锥套的影响;文献[5]总结了抽鞭现象的一般特点,指出了空中加油软管因控制不当发生抽鞭现象时,存在软管断裂的风险。但是这些研究都集中于定性分析加油软管存在的风险性,而没有指出定量评估指标和相应的评估方法。

空中加油机软管断裂事故是随机小概率事件,需要相当大的样本数才能确定其风险概率,很难进行风险评估,因此必须建立风险小概率事件的小样本评估模型。而极值理论主要对随机小样本及随机过程中的极值概率进行研究,目前被广泛应用于航空等重大事故以及各低频高危事件的风险定量分析[6-7]。本文针对极值理论中传统模型对样本辨识适应度低、评估误差大的缺陷,利用非线性优化模型对传统模型进行了改进,并采用LS算法和GA算法对文中非线性模型参数进行了对比辨识,以寻求风险概率的最优解;最后结合马尔科夫链综合评估模型,定量分析了空中加油软管断裂的风险概率,其对于保障受油机飞行安全具有重要的参考价值。

1 空中加油软管锥套动力学模型

1.1 软管锥套运动学分析

自主空中加油技术研究日益广泛,但是普遍存在软管锥套运动模型过于简单的问题。本文综合考虑加油机牵连运动、重力、大气扰动、加油机尾流等内外部因素的影响,将软管锥套假设为长度可变且质量集中于一点的N等段理想刚体串联组成[3],从而建立新的软管锥套运动模型,如图1所示。

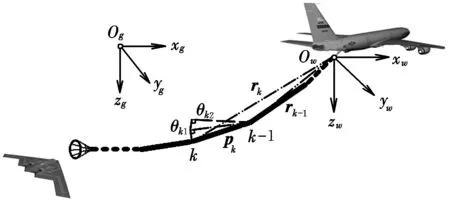
图1 空中加油软管锥套模型坐标系Fig.1 Reference frames of the hose-paradrogue model

图1中,地平系Ogxgygzg为惯性坐标系;拖拽点系Owxwywzw平行于航迹系,作为建模参考系;pk为刚体k-1指向刚体k的空间矢量;θk1和θk2分别为pk与拖拽点系的平面xwyw、平面xwzw的夹角;rk为刚体k在拖拽点系Owxwywzw中的位置矢量。

当加油机姿态发生变化,拖曳点系相对于地平系发生牵连转动,则可得第k阶刚体的运动学方程为:

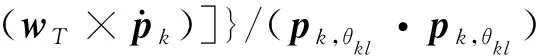
(1)

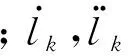
根据牛顿第二定律,对第k阶刚体进行受力分析,可得出关于刚体拉力的代数线性方程组:

-μk-1(nk·nk-1)tk-1+(μk+μk-1)tk-μk(nk·

(2)

式中,μk=1/mk;tk为第k阶刚体拉力矢量;Qk为刚体k所受外力;单位矢量nk=-pk/‖pk‖。

1.2 软管锥套外力分析

在空中加油过程中的对接阶段,若不对软管加以控制或者控制不当,作用于锥套的冲击力在扰流影响下将会导致软管发生抽鞭现象[5],软管上的拉力特别是末端刚体的拉力将急剧变化。当最大拉力达到10 kN左右时,软管将会破裂导致燃油泄漏[2],这不仅影响加油任务的完成,而且还将对受油机的飞行安全造成严重威胁。

由外力分析可知,式(2)中刚体k所受外力Qk包括第k阶刚体的重力和空气阻力Dk两部分:

Qk=mkg+(Dk+Dk-1)/2

(3)

由风洞实验可知,Dk与软管直径、长度、朝向角、大气密度等参数相关[3]。故锥套所受空气阻力大于软管各阶刚体的空气阻力Dk,导致与锥套连接的末端刚体所受外力QN最大。因此,本文以末端刚体的拉力极值作为软管拉力样本对软管进行风险定量评估。

2 风险评估方法

2.1 基于极值理论的概率评估方法

空中加油机软管断裂事故是随机小概率事件,为确定其风险概率,需要相当大的样本数,以致很难对其进行风险评估。而极值理论能够很好地解决风险小概率事件评估模型问题,目前被广泛应用于航空等重大事故以及自然灾害、铁路安全等低频高危事件的定量分析[6-7]。随机量的极值分布常趋向于一种发散的分布,Parprut 和Tarko采用了一种收敛的渐近线分布规律来近似表示,其分布函数可具体描述为[8]:

x=e-b/yc

(4)

式中,x为累积概率;y为软管拉力极值样本;b,c为调整参数。

由于拉力极值样本的精确分布难以获得,因此往往采用经验数据来对极值渐近分布进行拟合研究。拉力极值样本变量yi的经验概率pi可由下式计算得到[7]:

xi=pi=i/(n+1)

(5)

(6)

该线性模型在实际应用中误差较大,而且拉力极值yi在实际中会有特定的界限(不大于10 kN)。本文针对于此,首先对模型式(6)作如下改进:

(7)

式中,L为随机量的界限。

当软管发生抽鞭现象时,软管拉力极值样本的分布具有显著的非线性特性,而模型式(6)、式(7)对此很难进行有效地模型匹配,且存在误差大、适应度低的缺陷。因此本文利用非线性优化模型对极值理论中传统的线性模型进行了改进,建立了能精确反映样本具有非线性特性的多项式逼近模型,具体如下:

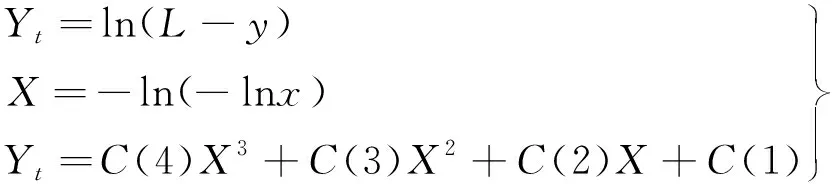
(8)

目标函数为已知拉力极值与逼近函数值f(x(i))之间误差的均方和:

(9)

以式(8)为软管拉力极值样本逼近模型,则样本超过极值发生的概率为:

(10)

求解目标函数式(9)的过程常局限于传统最小二乘法、极大似然法等非智能算法。这些非智能算法的辨识精确度比较依赖于所选取的初值,且初值的选取在许多情况下难以确定,对非线性模型参数的辨识精度较低。而GA算法具备很强的自适应智能搜索能力及全局优化能力,且对非线性问题的求解有很强的适用性。因此,本文选用GA算法进行加油机软管风险定量评估,并将式(9)设为GA算法的适应度函数。

由于统计分析中小样本的选取、极值模型的选择以及评估方法对结果的影响至关重要,所以在求出极值分布参数后,需进行拟合优度检验,本文采用图示法进行检验。

综上,本文所设计的评估方法具体步骤如下:

乾灵真火带着灼热气流朝·天南星妖扑去。那妖物定是知道这真火之厉害，面露惧色，一把扯过墨颜掷向熊熊燃烧的橘色火焰。

(1)确定软管拉力极值样本容量n,获取拉力极值采样值y1,y2,…,yn,将n个样本的观察值按递减顺序排列成y(1)>y(2)>…>y(i)>…>y(n);

(2)求出拉力极值样本y(1),y(2),…,y(n)对应的累积概率xi=pi=i/(n+1),i=1,2,…,n;

(3)确定样本的二维数组:(x(1),y(1)),(x(2),y(2)),…,(x(n),y(n)),确定目标函数,分别利用LS算法、GA算法对模型式(8)的参数进行辨识,确定极值分布模型;

(4)对步骤(3)所求出的拉力极值分布模型用图示法进行拟合优度检验,并对比分析检验结果。

2.2 马尔科夫链综合评估模型

马尔可夫链分析法是一种基于随机过程理论和概率论结合数学模型对客观对象发展过程中的数量关系进行研究的统计学方法[9]。

由马尔科夫链的性质可知,加油机软管断裂风险事故的发生过程可理解为是一种具有无后效性的随机过程,故可采用时间连续、状态离散的马尔科夫过程建立空中加油软管风险评估模型。图2为利用马尔可夫链建立的空中加油机软管因绞盘发生故障的状态转移图。

用x(t)表示t时刻加油机系统所处的状态,则:

系统的状态转移概率矩阵为:

(11)

假设初始时刻加油机安全正常工作,且绞盘故障不能修复,则有:

p0(t)=p{x(t)=0},p1(t)=p{x(t)=1}

p2(t)=p{x(t)=2},p3(t)=p{x(t)=3}

则:

p=[p0(t)p1(t)p2(t)p3(t)]

综上可得:

(12)

由式(12)即可得加油机对接时软管发生抽鞭断裂的风险概率。

3 仿真结果及分析

本文在进行空中加油软管锥套动态建模时,将软管假设为由16段刚体组成,软管的初始长度为14.33 m,外径为0.0673 m,单位长度质量为4 kg/m;锥套的质量为29.5 kg,直径为0.609 m;在对接过程中,加油机的飞行高度为2.3 km,飞行速度为159 m/s,对接加速度为3 m/s2。根据以上初始参数并结合Matlab/Simulink仿真平台来搭建仿真模型。

为获得软管拉力的有效极值,本文假设在加油机对接过程中,因绞盘突发故障,加油机无法对软管进行有效控制,导致在尾流影响下软管发生抽鞭现象,使软管拉力急剧增大。经过多次仿真采样获得100组末端刚体拉力极值,作为软管拉力的极值样本,应用于软管风险定量评估。由于加油机尾流场十分复杂,包括机翼和尾翼的翼尖涡流、机身紊流、大气扰流等。本文将加油机尾流场主要成分简化,采用Hallock-Burnham 模型[10]近似模拟加油机尾流。

根据上文利用极值理论对小样本计算小概率事件的评估方法,现将随机产生的软管拉力代入极值理论模型式(8),仿真计算后,可得极值样本分布如图3和图4所示。

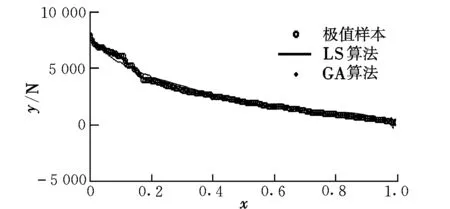
图4 软管拉力极值模型Fig.4 Extreme sample model of the hose’tension

统计结果表明,某型加油机的绞盘故障率为[9]:λ1=4.4×10-41/h。根据极值理论评估模型式(8),结合马尔科夫链综合评价模型式(12),利用GA算法可得空中加油软管发生抽鞭现象时断裂(软管拉力超过10 kN)的概率为:PGA=4.13×10-4;利用LS算法可计算得到加油机软管发生断裂的概率为:PLS=4.36×10-4。利用LS算法对非线性极值理论模型式(8)参数辨识的检验结果误差ELS如图5所示。由图5可知,误差较大;而利用GA算法计算所得误差EGA如图6所示。由图6可知,误差相对较小,计算结果更准确。因此,本文提出的方法能更好地对软管断裂风险进行定量评估。

4 结束语

本文提出了一种基于改进极值理论的空中加油软管风险定量评估方法。建立了空中加油软管锥套仿真模型,结合非线性优化极值模型和马尔科夫链综合评估方法,对比研究了GA算法和LS算法对评估模型辨识的适用性,计算了加油机软管抽鞭时断裂的风险概率。所得结果可为加油机软管的可靠性评估提供理论参考,并且文中采用的评估方法可推广到对类似随机小概率事件进行风险定量评估的研究。

参考文献：

[1] 窦和锋,董新民,薛建平,等.无人作战飞机空中加油建模与近距机动控制律设计[J].飞行力学,2013,31(4):326-330.

[2] Kapseong Ro,James W Kamman.Modeling and simulation of hose-paradrogue aerial refueling systems[J].Journal of Guidance, Control,and Dynamics,2010,33(1):53-63.

[3] 胡孟权,柳平,聂鑫,等.大气紊流对空中加油软管锥套运动的影响[J].飞行力学,2010,28(5):20-23.

[4] 张雷雨,张洪,杨洋,等.空中加油对接过程的动力学建模与仿真[J].航空学报,2012,33(7):1347-1353.

[5] 秦子增,郭鹏,陶午沙,等.抽鞭现象研究[J].国防科技大学学报,2010,32(6):64-70.

[6] Kam F C,Philip G.Using extreme value theory to measure value-at-risk for daily electricity spot prices[J].International Journal of Forecasting,2006,22(3):283-300.

[7] 徐浩军,朱建太.飞机纵向摆动及飞行安全评估[J].航空学报,2003,24(3):32-35.

[8] Parprut Songchitruksa,Tarko Andrew P.The extreme value theory approach to safety estimation[J].Accident Analysis and Prevention,2006,38(4):811-822.

[9] 刘东亮,徐浩军,张久星.多因素耦合复杂飞行情形风险定量评估方法[J].航空学报,2013,34(3):509-516.

[10] 陈博,董新民,徐跃鉴,等.加油机尾流场建模及受油机飞行安全性分析[J].系统仿真学报,2008,20(8):1994-2002.