增稳锥套与软管二级摆建模与仿真

石超，薛建平，董新民，王健，陈勇

(空军工程大学 航空航天工程学院，陕西 西安710038)

0 引言

对于“插头-锥套”自主空中加油方式来说，由于存在大气紊流［1］与受油机前体产生的头波［2］影响，再加上加油软管的柔性，导致加油锥套相对于加油机的空间位置不能固定，在一定范围内存在飘摆现象。由此可知，该加油方式存在两个缺点［3-4］:一是由于锥套存在飘摆现象，导致加油对接环节的时间较长;二是受油机接近加油锥套时，其前体头波可能诱发加油锥套震荡从而导致相关的加油事故。因此，增稳锥套的概念便应运而生。

Ellsworth等［5］早在1976年就着手研究对空中加油锥套进行引导与控制，设计出了一种用气动控制面代替稳定伞的加油锥套，并搭载在加油机CC-137上进行了一系列飞行试验。Williamson等［3］研究了通过操纵稳定伞对锥套进行主动增稳控制的设想，在低速锥套的基础上制造出一个可控锥套进行风洞试验，并通过控制方法的仿真获得了良好的控制效果。胡孟权等［6］通过对加油软管运动规律及平衡拖曳位置的研究，分析了软管的运动规律和锥套姿态的变化规律。王海涛等［7］针对软管锥套式空中加油系统的软管建模问题，提出了一种可变长度的多级串联理想单摆系软管运动模型，分析了加油机尾涡流场、滚转运动对软管锥套的动态影响及软管甩鞭现象的产生原因，并通过MATLAB仿真验证了所建模型的有效性。

对增稳锥套概念设计的研究文献越来越多，但都没有一个较好的仿真验证平台。虽然这些文献对软管锥套系统进行了分段建模研究，但大多把锥套视为一个只有气动阻力的质点。为此，本文提出了适用于仿真与风洞试验研究的增稳锥套与软管二级摆模型。此模型着重研究了增稳锥套的气动特性，而将软管视为等长的刚体杆。通过对此模型的建模与仿真研究，最终，获得了稳定气流中增稳锥套的静力平衡位置，为增稳锥套的进一步主动增稳控制方法研究奠定了仿真验证平台基础。

1 增稳锥套气动系数获取

1.1 增稳锥套三维数字模型的建立

本文所涉及到的增稳锥套模型的实物锥套原型如图1所示。

图1 软管式空中加油锥套Fig.1 Drogue in air refueling hose-drogue systems

本文结合图1中的加油锥套与文献［8］中风洞试验的905550锥套模型，使用三维数字固体几何建模软件UG建立了有8根支柱的简化三维数字锥套模型，并给出了一种加装“十字形”控制舵面增稳控制锥套的概念设计模型，如图2所示。

图2 普通锥套与加装舵面的增稳锥套三维模型Fig.2 3D models of drogue and stability drogue with control surfaces

1.2 CFD数值计算方法获取气动系数

1.2.1 数值计算结果

在Ma=0.4无干扰自由来流条件下，本文采用CFD方法分别计算了增稳锥套在6种迎角下的阻力系数CD、升力系数CL以及俯仰力矩系数Cm，所有计算中舵偏均为零。由于在实际加油条件下，锥套的迎角不超过5°，故选取 α =0°，1°，2°，3°，4°，5°这6 个迎角条件进行数值计算。在锥套体坐标系内，CFD数值计算所得6种迎角下增稳锥套的阻力系数、升力系数及俯仰力矩系数如表1所示。

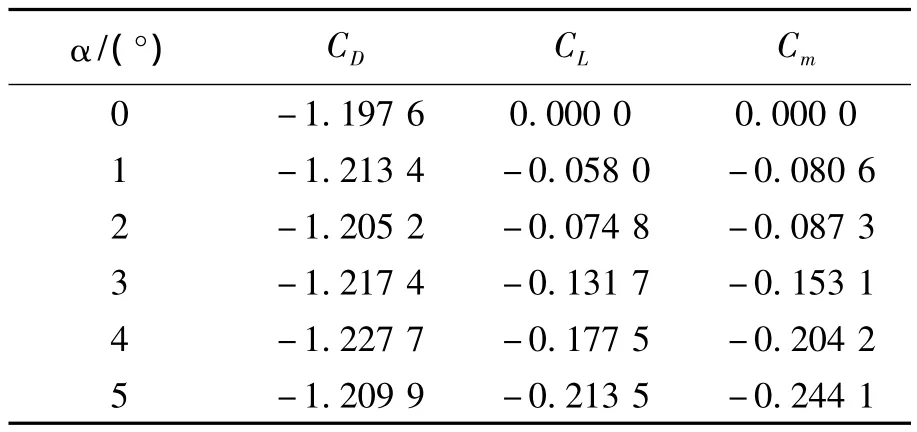
表1 增稳锥套在不同迎角下的气动系数Table 1 Aerodynamic coefficients of stability augmentation drogue at different angle of attack

图3和图4分别为增稳锥套在不同迎角下的阻力系数曲线、升力系数曲线及俯仰力矩系数曲线。

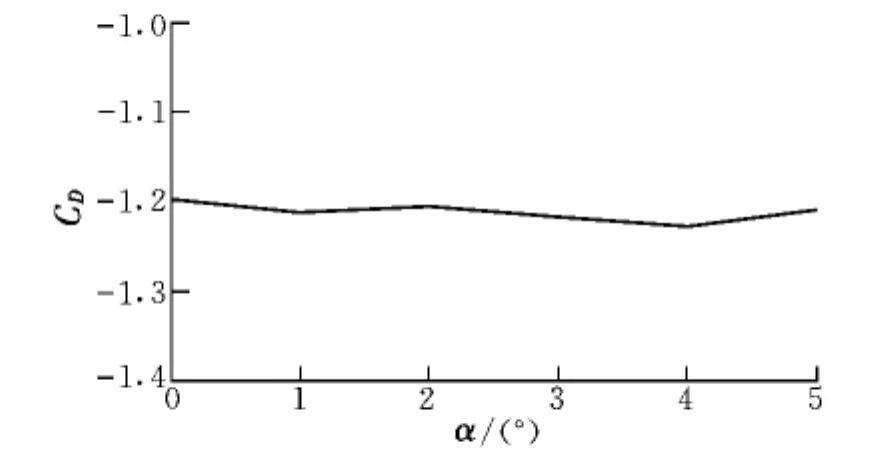
图3 增稳锥套在不同迎角下的阻力系数曲线Fig.3 Drag coefficient curve of stability augmentation drogue at different angle of attack

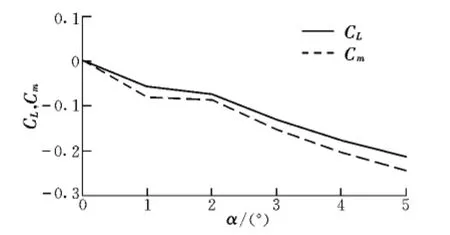
图4 增稳锥套在不同迎角下的升力系数和俯仰力矩系数曲线Fig.4 Curves of lift and pitch moment coefficient of stability augmentation drogue at different angle of attack

1.2.2 CFD方法的有效性验证

本文将锥套稳定伞阻力系数作为验证对象。根据文献［8］给出的经验公式可知，本文锥套稳定伞阻力系数的预测值为:

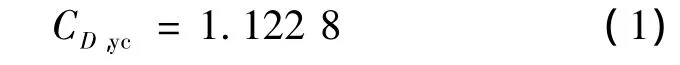
其与计算所得稳定伞阻力系数的平均值1.163 6误差3.63%，足以说明本文所用CFD方法的有效性。

1.3 气动系数线性拟合

由图3和图4可知，迎角在0°～5°内，增稳锥套阻力系数、升力系数及俯仰力矩系数均与迎角呈近似线性关系。故采用一元线性回归方法［9］分别对这三个系数进行线性拟合。拟合结果为:

2 二级摆运动建模

2.1 建模假设与坐标定义

在给出“软管-锥套”二级摆模型前，为了简化所研究问题的复杂性，进行如下假设:加油机定直平飞;将软管视为等长刚体管，并忽略其气动特性;认为地面坐标系为惯性坐标系;刚体管与加油吊舱间用假设的球形接头连接。增稳锥套与软管二级摆模型如图5所示。

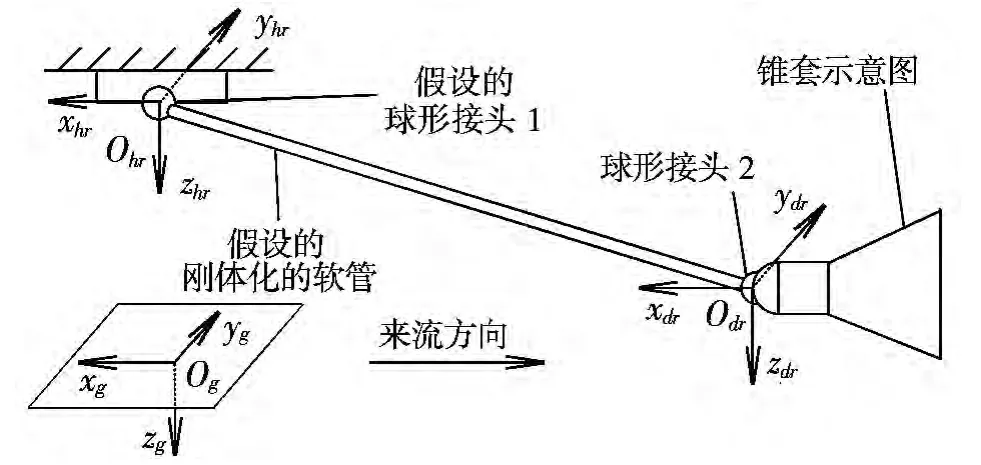
图5 二级摆模型及坐标关系示意图Fig.5 Schematic diagram of the double pendulum model and coordinate system

如图5所示，令地轴系Ogxgygzg为惯性系，管参系Ohrxhryhrzhr与锥参系Odrxdrydrzdr的原点分别为球形接头1与2的球心，且都与惯性系平行。本文研究还涉及到锥体系Odxdydzd与管体系Ohxhyhzh。锥体系原点与锥参系相同，xd轴与锥套中轴线重合，指向刚体管为正，yd轴与惯性系yg平行，zd由右手定则确定。管体系与锥体系定义方法相同，其原点在球形接头1球心处。

2.2 动力学方程

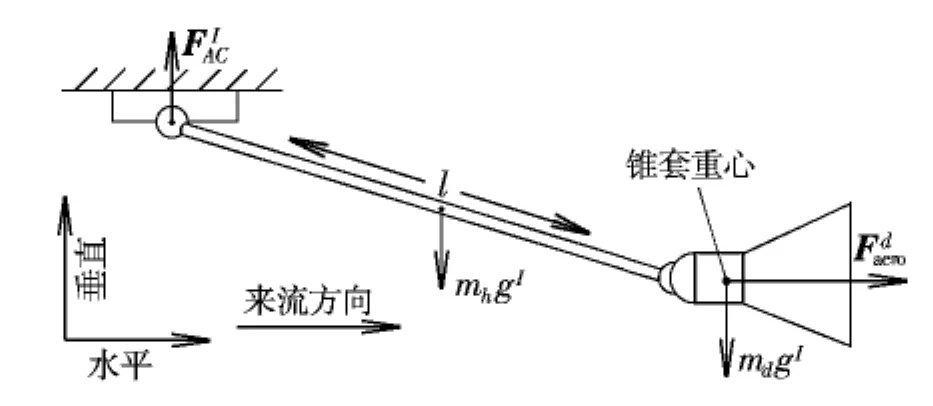
图6 二级摆动力学模型平面示意图Fig.6 Schematic diagram of vertical plane of the double pendulum dynamics model

作用在球形接头1球心处的合力与合力矩方程分别为:

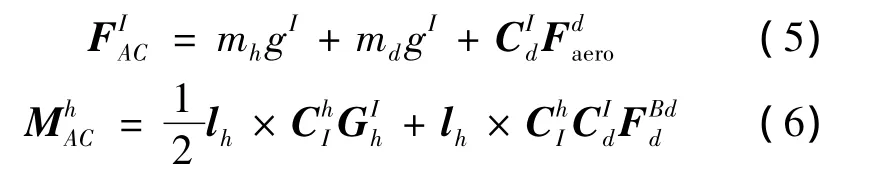
作用在球形接头2球心处的合力与合力矩方程为:

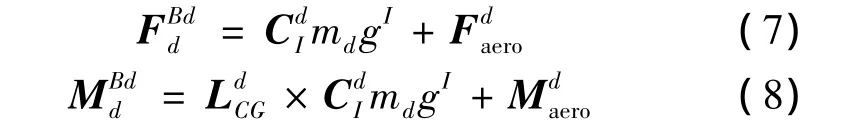
增稳锥套绕球形接头2球心转动的动力学微分方程为:

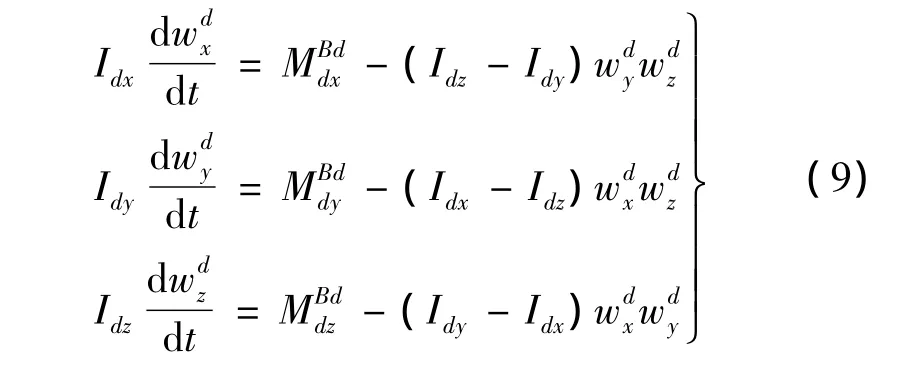
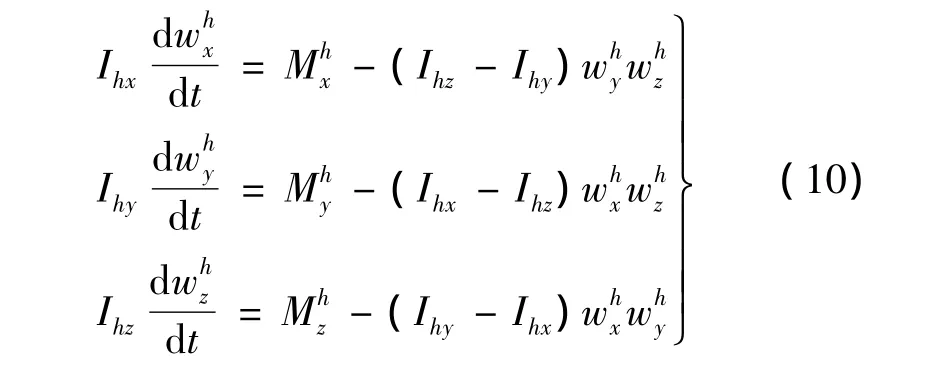
刚体管绕球形接头1球心转动的动力学微分方程为:式中:Ihx，Ihy，Ihz为刚体管绕其三个惯性主轴(在管体系内)的转动惯量为刚体管绕接头1球心的合力矩在管体系三个主轴上的分量;为刚体管绕其三个主轴的转动角速度分量。

2.3 运动学方程

本文采用四元数［10］解算刚体管与增稳锥套姿态。管参系中，刚体管绕球形接头1球心转动的四元数微分方程为:

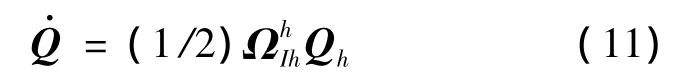
式中:Qh为刚体管单位四元数姿态为刚体管角速度矢量四元数矩阵形式，其表达式为:

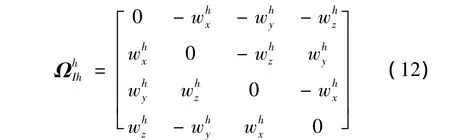
锥参系中，增稳锥套绕球形接头2球心转动的四元数微分方程为:

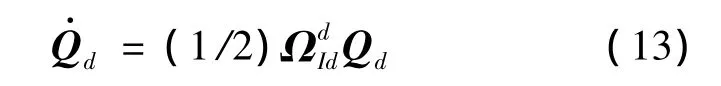
式中:Qd为刚体管单位四元数姿态;为增稳锥套角速度矢量的四元数矩阵形式，其表达式为:

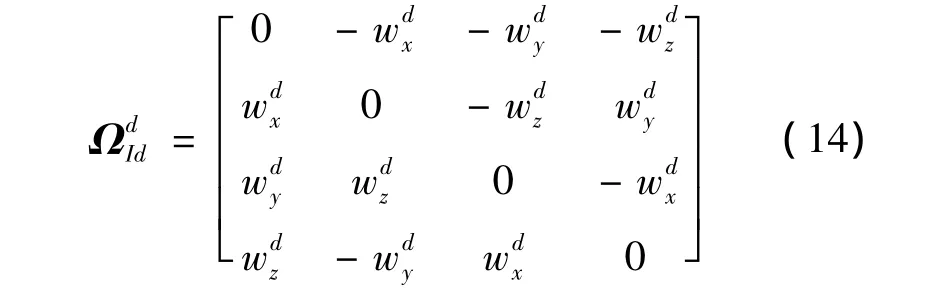
给定增稳锥套和刚体管的初始位姿，联立求解式(9)～式(11)及式(13)，即可计算出二级摆模型实时位姿。

3 仿真结果及分析

根据以上二级摆运动模型搭建Simunlink仿真模型。本文通过管参系Ohrxhrzhr平面内二级摆运动仿真，旨在获得稳定来流中增稳锥套相对于加油机吊舱的稳定平衡位置。

增稳锥套与刚体管的特性参数如下:刚体管长度30.48 m;刚体管直径0.08 m;刚体管满油密度6.64 kg˙m－1;增稳锥套质量32.09 kg;增稳锥套xd轴重心位置0.44 m。

仿真初始条件如下:稳定来流马赫数Ma=0.4;刚体管初始俯仰角20°;增稳锥套初始俯仰角0°;刚体管初始俯仰角速度0 rad˙s－1;增稳锥套初始俯仰角速度 0 rad˙s－1。

在初始条件下，使用拟合所得气动系数和二级摆特性参数进行仿真，得到管参系Ohrxhrzhr平面内锥套重心运动轨迹，如图7所示。

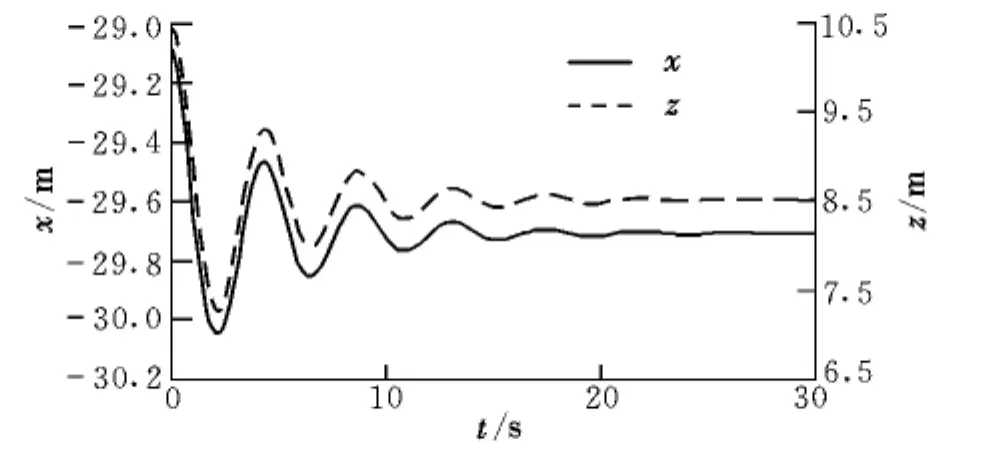
图7 增稳锥套重心运动轨迹Fig.7 Trajectory of the center of stability drogue gravity

由图7可知，仿真进行了30 s后，增稳锥套处于稳定平衡状态。表2给出了管参系内二级摆稳定参数。

表2 二级摆稳定参数Table 2 Stability parameters of double pendulum

为了验证稳定参数的可靠性，将稳定俯仰角与俯仰角速度作为初始条件，再次进行仿真，得到管参系Ohrxhrzhr平面内增稳锥套重心运动轨迹如图8所示。

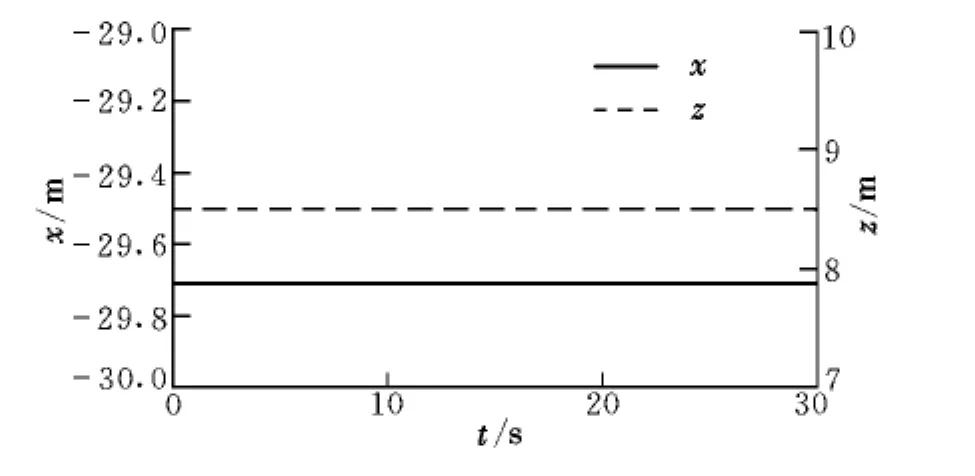
图8 增稳锥套重心运动轨迹Fig.8 Trajectory of the center of stability drogue gravity

从图8可以看出，仿真获得的稳定参数可靠，同时也说明了所搭建的增稳锥套二级摆仿真验证平台的有效性。

4 结束语

本文提出了一种简化的软管与增稳锥套二级摆模型，建立了其运动模型，并进行了仿真研究，最终获得了稳定气流中增稳锥套的稳定平衡位置，为增稳锥套的进一步主动增稳控制方法研究奠定了仿真验证平台基础。下一步的工作可在如下两方面开展:研究在不同迎角与不同舵偏角下，增稳锥套的气动特性，为其增稳控制提供气动参数;在其气动特性充分研究的基础上，研究增稳锥套的控制算法，达到稳定锥套的目的。

［1］ 张雷雨，张洪，杨洋，等.空中加油对接过程的动力学建模与仿真［J］.航空学报，2012，33(7):1347-1354.

［2］ Dogan A，Blake W.Modeling of bow wave effect in aerial refueling［C］//AIAA Atmospheric Flight Mechanics Conference.Toronto，Ontario Canada，2010.

［3］ Williamson W R，Reed E，Glenn G J，et al.Controllable drogue for automated aerial refueling［J］.Journal of Aircraft，2010，47(2):515-527.

［4］ 刘曌，周春华，袁锁中.软管式自主空中加油飞行控制系统与仿真研究［J］.系统仿真学报，2012，24(10):2054-2059.

［5］ Ellsworth J A，Fox W R，Lovendahl D E，et al.Guided drogue flight test report［R］.NAVY TRE-23027，1978.

［6］ 胡孟权，聂鑫，王丽明.插头-锥管式空中加油软管平衡拖曳位置的计算［J］.空军工程大学学报，2009，10(5):22-26.

［7］ 王海涛，董新民，窦和锋，等.软管锥套式空中加油系统建模与特性分析［J］.北京航空航天大学学报，2014，40(1):92-98.

［8］ Kapseong Ro，Basaran E，Kamman J W.Aerodynamic characteristics of paradrogue assembly in an aerial refueling system［J］.Journal of Aircraft，2007，44(3):963-970.

［9］ 汪荣鑫.数理统计［M］.西安:西安交通大学出版社，1986:174-185.

［10］范奎武.用四元数描述飞行器姿态时的几个基本问题［J］.航天控制，2012，30(4):49-53.