空中加油锥套支柱数对稳定伞阻力系数影响研究
石超, 薛建平, 董新民, 刘娇龙
(空军工程大学 航空航天工程学院, 陕西 西安 710038)
0 引言
在未来的无人机军事行动中,进行空中加油是必须考虑的重要问题。自2000年开始,无人机空中加油已经引起NASA,USAF和USNAVY等主要研究机构的关注,并进行了一系列的探索[1]。目前,“软管-锥套-探头”系统是普遍采用的一种空中加油系统。空中加油过程包括编队、对接、加油及脱离四个阶段,其中对接过程是实现空中加油的关键。
对锥套气动阻力特性的充分掌握,是成功实现自主空中加油的重要要求,能够提高自主空中加油模型在控制律综合设计和仿真中的精确性。近年来,越来越多的研究者开始关注自主空中加油技术。张雷雨等[2]针对对接碰撞过程中锥套的受力情况进行建模分析,提出了一种计算碰撞力的方法。胡孟权等[3]通过对加油软管运动规律及平衡拖曳位置的研究,分析了软管的运动规律和锥套姿态的变化规律。NASA德莱顿飞行研究中心通过一系列的飞行测试,分别研究了两种空中加油锥套在不同飞行条件下的气动阻力与阻力系数[4]。Kapseong等[5]在风洞试验数据的基础上,通过数理统计的方法提出了一种锥套气动阻力系数计算的经验公式,为锥套的设计提供了参考。
对锥套运动规律及其阻力系数研究的文献越来越多,但关注影响锥套阻力系数的因素的文献却很少,为此,本文针对锥套支柱根数对锥套稳定伞阻力系数的影响进行研究。
1 锥套三维数字模型的建立
所研究的锥套模型的原型如图1所示。其中,锥套前端的稳定伞是锥套产生阻力的主要部件。当受油探头与加油锥套对接时,稳定伞起到稳定软管和锥套的作用。当锥套的气动阻力较小时,受油探头需要以较大的速度才能撞开锥套底部的加油开关锁,因此,受油探头所产生的“头波”会更加剧烈[6],其气流对锥套产生的影响会增大,导致锥套不稳定,增加了加受油的难度。当锥套的气动阻力较大时,软管和锥套的稳定性会增强,有利于对接的顺利完成,降低了加受油难度。

图1 软管式空中加油锥套Fig.1 Hose-type aerial refueling drogue
本文选取文献[5]中风洞试验的903050锥套模型作为研究对象,采用三维数字固体几何建模软件UG建立了8根、12根、18根支柱的903050锥套模型。其中,903050锥套型号的命名方法为:90代表支柱的安装角(即90°),30代表稳定伞的特征长度(即3.0 in),50代表稳定伞之间相隔的圆周角度(即5.0°),如图2所示。为了方便表示,本文将8根、12根和18根支柱的903050锥套模型分别编号为:90305008,90305012和90305018,最后两位数字代表支柱根数。
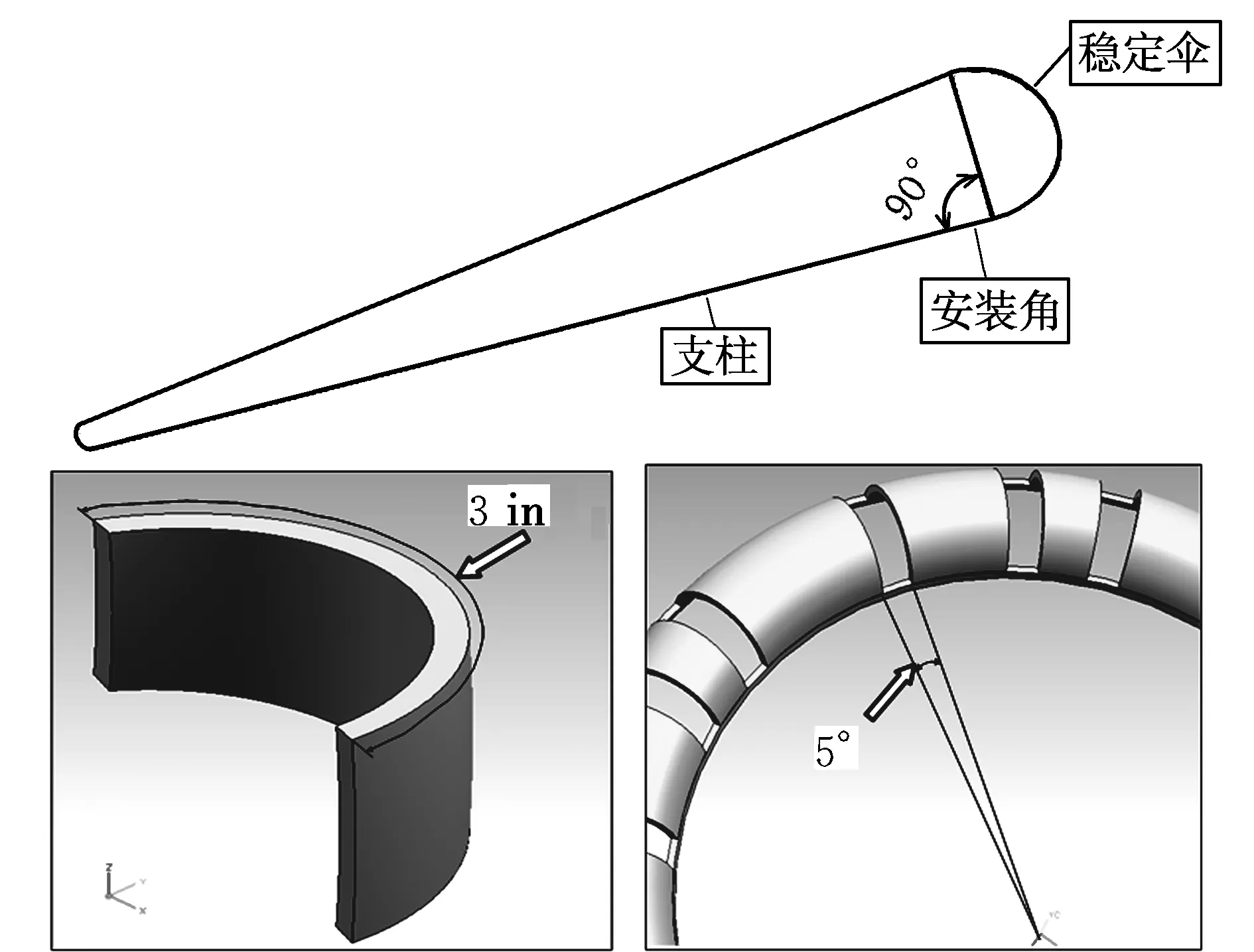
图2 903050模型编号示意图Fig.2 Sketch map of 903050 model number
2 CFD数值计算及方法验证
在研究锥套支柱数对锥套前端稳定伞阻力系数的影响前,有必要对所建三维数字模型的精确性和CFD计算方法的正确性进行合理验证。因此,选用与风洞试验中的锥套模型具有相同支柱根数的锥套三维数字模型90305008进行CFD数值计算,把计算所得稳定伞阻力系数与风洞试验中所得的阻力系数进行比较,以比较误差作为验证的依据。
2.1 网格生成
采用CFD的前处理器ICEM生成锥套三维数字模型的计算域呈圆柱体形状,直径为9.6 m,长15.24 m,如图3所示,上椭圆网格区域代表速度入口,下椭圆网格区域代表压力出口,其余网格区域代表远场区域,所有锥套模型的网格生成都使用与此相同的计算域。
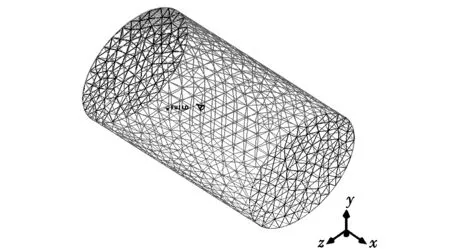
图3 锥套模型的计算域Fig.3 Computational domain of drogue model
锥套的几何构造比较复杂,为此,在计算域中选用八叉树方法生成非结构的四面体网格。生成网格的数目越多对计算机性能要求越高,并且计算时间会更长。对此,根据所使用的计算机,在保证合理计算精度的前提下,不断调整网格的大小和密度,使网格数保持在3.0×106~3.5×106之间。由于锥套前端的稳定伞呈不对称分布,因此,不能使用周期性条件来减小计算域并缩减网格数目。锥套周围的网格分布如图4所示。
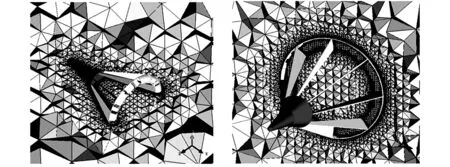
图4 锥套周围的网格分布Fig.4 Grid distribution around drogue model
2.2 计算方法
根据文献[5]的风洞试验条件,进行如下假设:Fluent里的流体是不可压缩的、稳定的三维粘性流,并忽略重力的影响。计算方法设置如下:
(1)湍流模型使用可实现的k-epsilon湍流模型。(2)设置流体材料属性:材料设为空气,密度选项为默认密度1.225 kg/m3,粘性选项为默认粘性1.789 4×10-5kg/m·s-1。(3)计算域入口边界条件设为速度入口,出口边界条件设为压力出口。(4)壁面条件选为无滑移条件,壁面粗糙度设为默认值0.5,其他标量采用不可渗透的壁面条件。(5)差分格式的选择:压力插值采用默认的标准方法,压力-速度耦合采用PISO方法,动量、湍流耗损率以及湍流动能均采用二阶迎风格式。(6)松弛因子设为默认值,因为默认值是Fluent软件根据前面的设置自动调制的最优松弛因子。(7)迭代计算2 500次后的收敛准则设置为残差小于10-4。
2.3 计算结果与方法验证
由于风洞试验中所使用的风速范围为25~43 m/s,为了模拟风洞试验中的空速条件,在Fluent中进行了5种速度下的数值计算。
通过CFD分析,可使流场特性的数值解图形可视化,有助于直观观察锥套阻力的分布,进一步理解稳定伞是锥套产生阻力的主要部件以及锥套支柱数是影响稳定伞阻力系数的原因。90305008锥套模型周围流场的等压线以及锥套表面的压力分布如图5所示,其周围气流速度向量和稳定伞内外的速度向量分别如图6所示。图7为90305008锥套数值计算所得阻力系数曲线图。
风洞试验与CFD数值计算所得的锥套前端稳定伞阻力系数的平均值分别为0.949 7和0.878 7,其误差为7.476 0%。经分析,风洞试验中的锥套稳定伞是尼龙布制成的,而其三维数字模型是根据文献[7]风洞试验中稳定伞轮廓外形建立的,由此可知,此误差主要来源于三维数字模型中锥套稳定伞的建模误差。这个较小的误差,表明了CFD数值计算方法的正确性,可以满足数值计算对精度的要求。
在支柱数对稳定伞阻力系数影响的研究中,不同支柱数的锥套模型使用相同的稳定伞模型,以此来减小稳定伞建模误差对后续研究的影响。
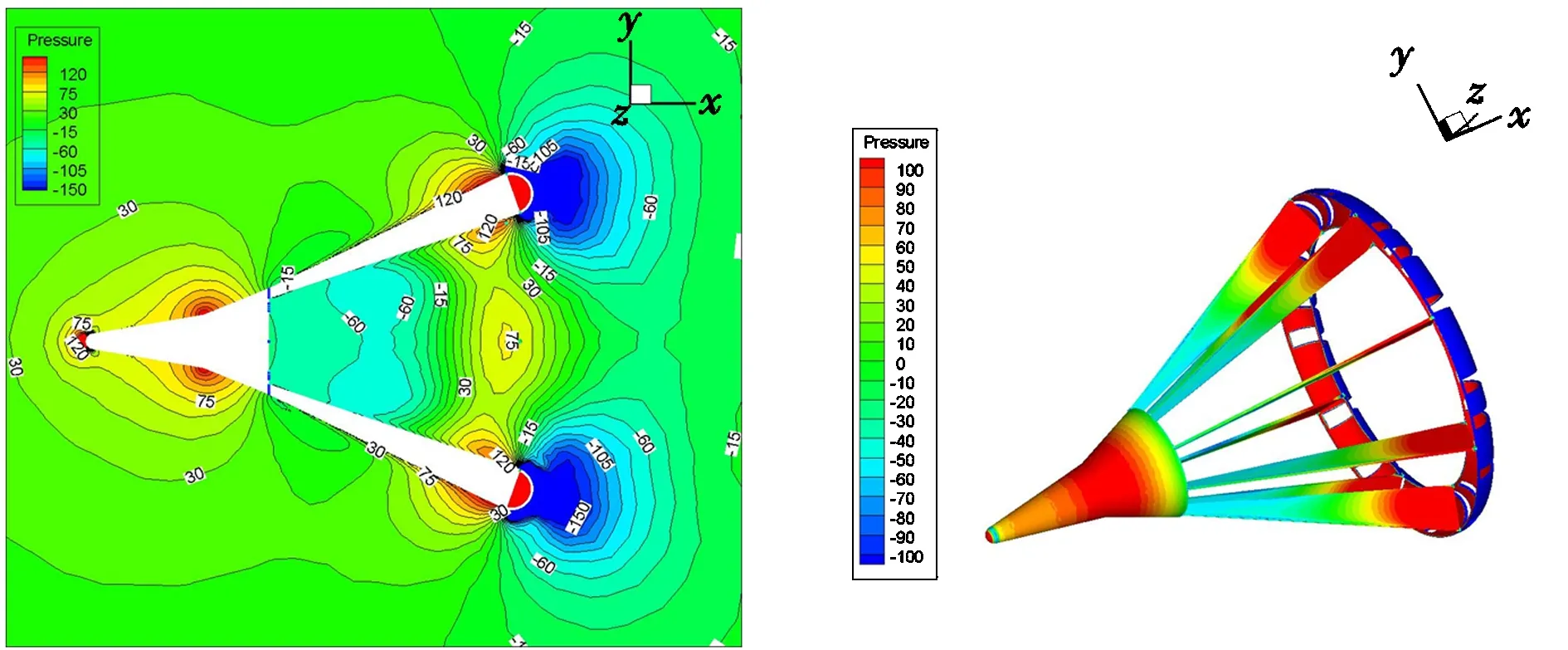
图5 锥套周围流场及表面的压力分布Fig.5 Flow field around the drogue and pressure distribution on the surface
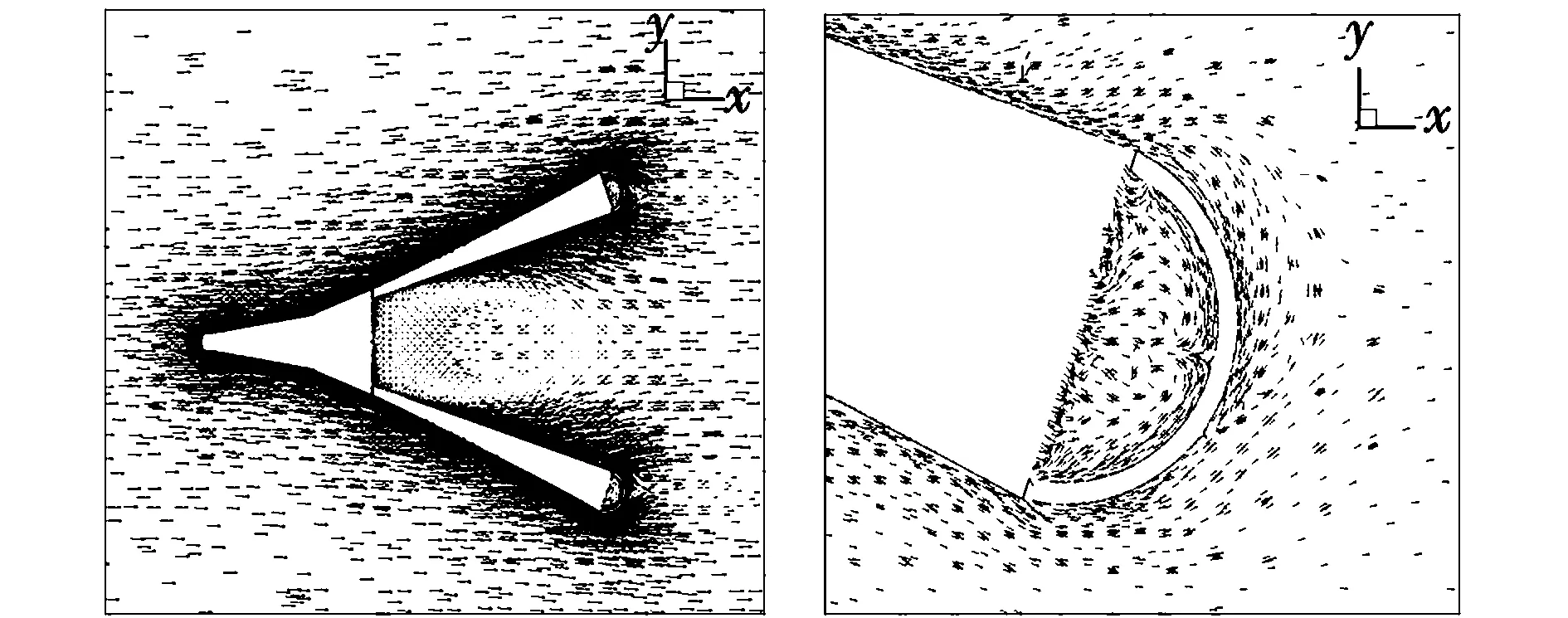
图6 锥套周围流场的速度分布Fig.6 Velocity vector distribution around drogue model
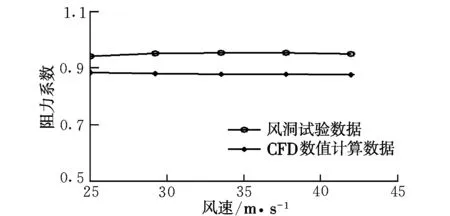
图7 90305008锥套稳定伞阻力系数曲线Fig.7 Drag coefficient curves of 90305008 drogue canopy
3 数值计算及二元方差分析
3.1 数值计算
研究锥套支柱数对前端稳定伞的阻力系数是否有影响以及影响规律,采用所建立的三个不同支柱数锥套模型,CFD数值计算过程中,网格的生成方法保持不变。图8为不同支柱数模型稳定伞阻力系数曲线图。表1为90305008模型、90305012模型和90305018模型在5种空速下数值计算所得锥套稳定伞的阻力系数值。
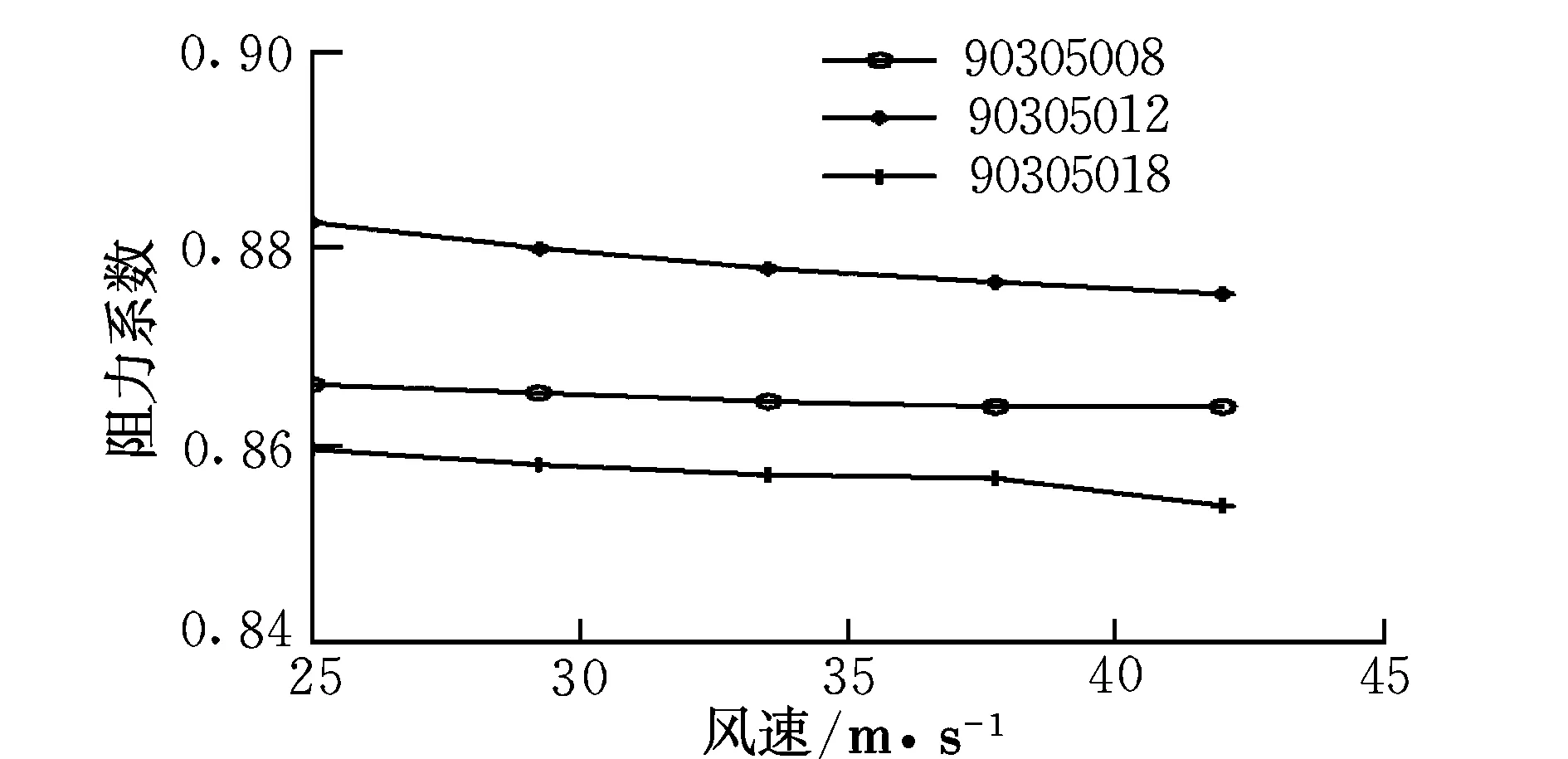
图8 不同支柱数模型稳定伞的阻力系数曲线Fig.8 Canopy drag coefficient curves of drogues with various strut number
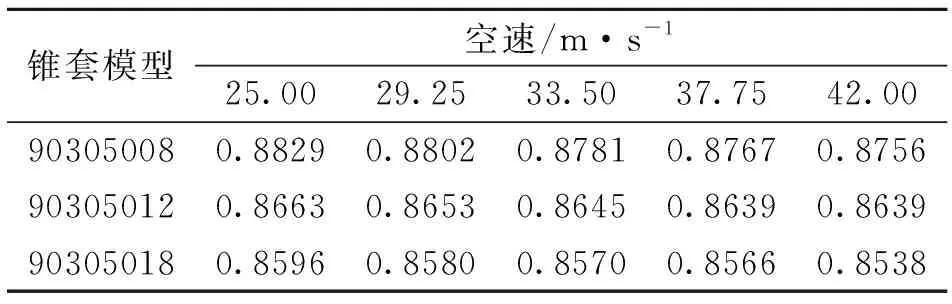
锥套模型 空速/m·s-125.0029.2533.5037.7542.00903050080.88290.88020.87810.87670.8756 903050120.86630.86530.86450.86390.8639 903050180.85960.85800.85700.85660.8538
3.2 二元方差分析
本文只针对锥套支柱数对稳定伞阻力系数的影响进行研究。由于研究中还涉及到空速,因此采用二元方差分析方法,从计算结果中分离出支柱数这个变量的影响。
3.2.1 非重复二元方差分析
二元方差分析可判断两个因素对实验结果的影响是否显著[8]。本文采用的非重复二元方差分析方法,在每一种水平上进行一次稳定伞阻力系数的数值计算,其方差分析见表2。
因子A的拒绝域为:
WA:FA≥Fα(r-1,(r-1)(s-1))
(1)
因子B的拒绝域为:
WB:FB≥Fα(s-1,(r-1)(s-1))
(2)
式中,F表示F检验方法;α表示显著性水平,即置信概率为(1-α)。一般情况下,α取0.05和0.01。当α=0.05时,置信概率为95%,表示影响显著;当α=0.01时,置信概率为99%,表示影响十分显著。

表2 非重复二元方差分析Table 2 Dualistic variance analysis without repetition
注:r为因子A的水平数;s为因子B的水平数。
3.2.2 数值计算结果的二元方差分析
对锥套支柱数与空速这两个变量因素进行非重复数值计算的二元方差分析。因子A为锥套支柱数,取3种水平,即r=3;因子B为空速,取5种水平,即s=5。根据表2的原理建立方差分析如表3所示。
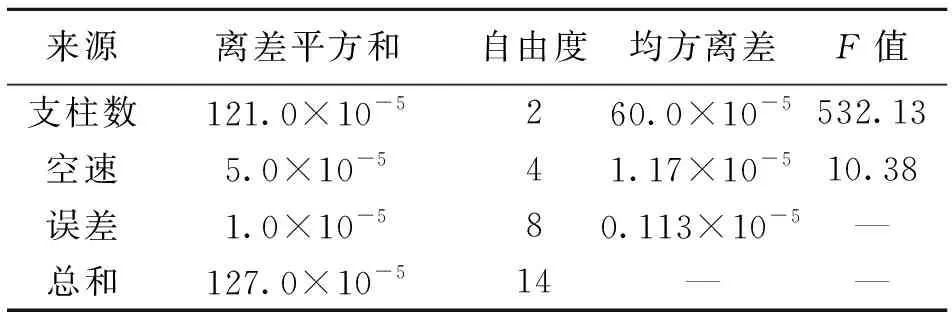
表3 对稳定伞阻力系数影响的方差分析Table 3 Variance analysis for impact on canopy drag coefficient
(1)给定α=0.05
WA:FA≥Fα(r-1,(r-1)(s-1))
=F0.05(2,8)=4.46
由表3可知:FA=532.13>4.46,表明锥套支柱数的不同对稳定伞阻力系数有显著的影响。
(2)给定α=0.01
WA:FA≥Fα(r-1,(r-1)(s-1))
=F0.01(2,8)=8.65
由表3可知:FA=532.13>8.65,表明锥套支柱数的不同对稳定伞阻力系数有十分显著的影响。
综上所述,锥套支柱数对稳定伞阻力系数有十分显著的影响,支柱数越多,稳定伞的阻力系数越小。
4 结束语
本文在对903050锥套模型进行CFD数值计算的基础上,采用非重复的二元方差分析方法,针对锥套支柱数对锥套稳定伞阻力系数的影响进行了研究。研究结果表明,空中加油锥套的支柱数对锥套稳定伞的阻力系数有十分显著的影响,支柱数越多,稳定伞的阻力系数越小。这对提高自主空中加油模型在控制律综合设计和仿真中的精确性具有十分重要的意义。进一步的工作可从以下两方面深入:对于锥套稳定伞三维数字模型的精确度有必要进行风洞试验研究,以此来减小建模误差;增加不同支柱数锥套模型对比的组数,进一步研究锥套支柱数对稳定伞阻力系数影响的详细规律。
参考文献:
[1] Hansen J L,Murray J E,Campos N V.The NASA Dryden AAR project: a flight test approach to an aerial refueling system[R].AIAA-2004-4939,2004.
[2] 张雷雨,张洪,杨洋,等.空中加油对接过程的动力学建模与仿真[J].航空学报,2012,33(7):1347-1354.
[3] 胡孟权,聂鑫,王丽明.插头-锥管式空中加油软管平衡拖曳位置的计算[J].空军工程大学学报,2009,10(5):22-26.
[4] Vachon M J,Ray R J.Calculated drag of an aerial refueling assembly through airplane performance analysis[R].AIAA-2004-0381,2004.
[5] Kapseong R,Basaran E,James W K.Aerodynamic characteristics of paradrogue assembly in an aerial refueling system [J].Journal of Aircraft,2007,44(3):963-970.
[6] Vassberg J C,Yeh D T,Blair A J.Numerical simulations of KC-10 in flight refueling hose-drogue dynamics with an approaching F/A-18D receiver aircraft[R].AIAA-2005-4605,2005.
[7] Shigeo Hayashibara,James Austin.Simulation-based design (SBD) application for a mid-air aerial refueling paradrogue system[R].AIAA-2006-7770,2006.
[8] 尹凤敏.两栖作战编队防空火力协同的交互性分析[J].舰船电子工程,2010,30(9):45-47.

