永久性最低提取利益保证变额年金的公平保证费用定价

李秀芳,孙 芳,焦永刚

（南开大学，天津 300000)

一、研究背景

2011年5月，《关于发展变额年金保险试点的通知》和《变额年金保险管理暂行办法》颁布，同年6月-7月，两家首批变额年金试点公司工银安盛人寿（原金盛人寿）和中美联泰大都会人寿分别推出“保得赢”和“步步稳赢”的变额年金产品。2012年3月，华泰人寿推出“吉年保利”变额年金产品。2013年5月，中美联泰大都会人寿公布的变额年金单位价格显示，稳赢利益投资账户卖出价较去年同期增长1.5-2个百分点（数据来源：21财经聚合搜索）。工银安盛人寿的和谐投资账户卖出价较去年同期增长约0.5个百分点。但是，变额年金同时是一款风险较大的产品，在金融危机中易受到较大冲击，其风险成为首要考虑的问题。

关于具有最低收益保证变额年金的定价问题吸引了很多国内外学者。早在1977年，Boyle和Schwartz等人将金融中的布莱克-斯科尔顿模型利用到了年金的定价问题。 Milevsky、Posner（2001）用风险中性理论对最低身故利益保证（Guaranteed Minimum Death Benefit，GMDB）进行了定价。Mudavanhu、Zhou（2002）在 GMDB 定价模型中考虑了死亡率、失效率以及退保因素。国内变额年金保险市场发展还处于初级阶段，关于变额年金领域的研究和文献较少。李冰清、廖朴（2012）研究了变额年金业务的风险问题。刘迪（2011）研究了具有最低提取利益保证变额年金的定价，但是没有考虑保单持有人在保险期限内的生存和死亡概率，不符合实际。李方方（2012）在常利率和波动率下考虑了最低提取利益保证的重置条款、奖励条款、惩罚条款加入了定价模型。

2003年，在美国市场上出现的一种新型的GMWB产品，即永久性有最低提取保证的变额年金（Guaranteed Lifelong Withdrawal Benefits，GLWB）。该产品保证保单持有人每年可以领取最低给付保证额度的年金直至死亡，每年取款额有限制，而总取款额无限制。提供GLWB的变额年金保险产品除了风险较高之外，可以有效地降低投保人的长寿风险，一定程度上非常符合当前消费者需求，如今已经逐渐占领了美国变额年金保险市场，但是相关的定价研究较少。Gabriella Piscopo（2009）研究了在固定利率和固定波动率下GLWB的定价。本文在已有的研究基础上，对永久性最低领取利益保证变额年金产品进行定价研究，改进Gabriella Piscopo（2009）定价模型中常利率和常数波动率的弊端，运用Regime-Switching模型进行数值模拟，考虑经济状态转变对保证费用的影响，得出更公平、更符合实际的定价，为国内保险公司设计开发此类产品提供一些建议和理论指导。

二、变额年金的定价

假设年龄为的人初始时刻以趸缴一笔保费购买变额年金产品，保单持有人每年可以领取最低提取保证额度的年金。

1、资产模型与假设

假设市场是无套利市场，持续交易，忽略交易费用,允许卖空，无税收。在风险中性概率空间中（W，Ft｛｝，Q），Q为风险中性测度。记St表示t时刻保单持有人变额年金账户中未提取任何费用前的资产价值，在风险中性测度Q下满足如下随机微分方程：

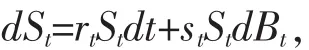
变额年金账户提供两种支出：保险公司最低给付保证的费用（为账户余额的一定比例，记为a）和保单持有人在时刻的提取款gt。因此考虑上述两种支出后，投保人变额年金账户可描述为：

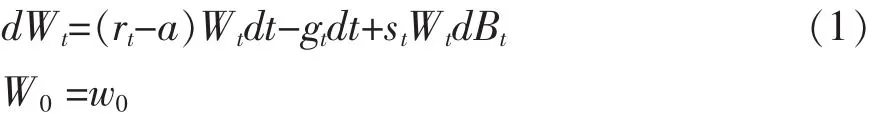
Wt表示t时刻变额年金账户余额。（1）式在t＜t0时成立，其中t0表示Wt第一次达到0时的时刻。若t＜t0，则Wt=0。在有最低给付保证的变额年金产品中，若t＞t0，即Wt=0时，投保人每年可以获得最低给付保证 G。提取款 gt在 t＜t0时，原则上可以取［0，Wt］的任意值，但是若时gt＞G，保险公司收取额外的保险费用，目的是不鼓励投保人过早提取完年金。

我们进一步假设死亡事件与金融事件为不相关事件。Tx令表示年龄为x岁的人的剩余寿命，tPx表示x岁的人在t年后仍然生存的概率，即tPx=P（Tx＞t），t=0,1,L,n-x。 进一步，我们用tPx表示x岁的人在接下来t年内死亡的概率，特别地对t=1，我们简单地用qx表示x岁的人在一年内死亡的概率，即qx=P（Tx＜t）。因此，对于x岁的人在t年后的一年内死亡的概率表示为tpxqx+t，即tpxqx+t=P（t＜Tx＜t+1）。

2、GLWB公平保证费用定价

上述的投资动态模型与Chen和Forsyth（2008）、Gerber和 Shiu （2003）等人的定价模型一致。追随前面的保险文献，我们假设存在一风险中性测度，在此风险测度下支付流可以用风险中性计算公式定价为期望贴现值，而这种风险中性测度的存在意味着市场为无套利的。我们讨论在静态决策下GLWB的公平保证费用定价问题。假设投保人以最低保证额度领取年金，即gt=G。在静态决策下（1）式表示为：

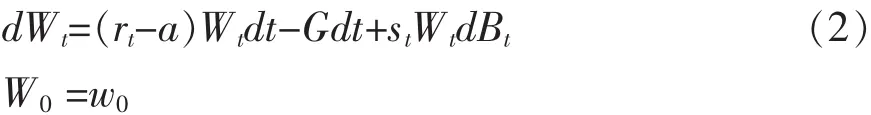
其中对于 t3t0，Wt=0

GLWB允许投保人在生存时每年领取最低给付保证的年金，死亡时将账户余额全部返还。因此保单持有人既享有生存利益又享有死亡价值。V0令表示GLWB在t=0时的贴现价值，则V0应为保单持有人生存时的领取的总年金期望贴现值与其死亡时年金账户余额期望贴现值之和，即V0=LB0+DB0（其中LB0表示保单持有人生存时的领取的总年金贴现值，DB0表示保单持有人死亡时能够遗留下的遗产贴现值）。

其中n为保单持有人可能活的最大年龄。下面计算DB0。因为永久性最低给付保证变额年金承诺在保单持有人死亡时若账户余额不为空，则账户余额全部返还。假设保单持有人在时间t=T时死亡，则保险公司返还给保单持有人指定的遗产继承人的金额应为 Max（WT，0），即：

DBT=Max（WT，0）

通过 Karatzas和 Shreve（1992），可推导出：

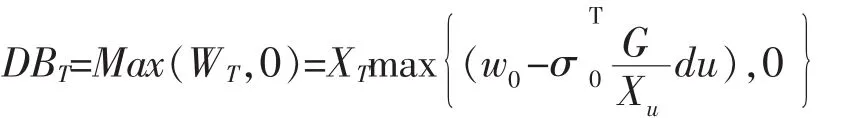
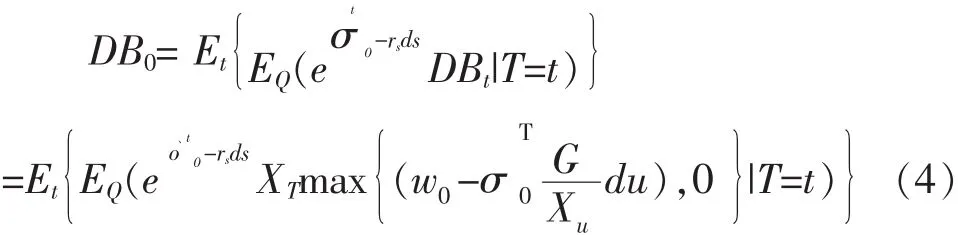
为了化简上式，引入测度Qs，利用测度变换从Q 到 Qs，

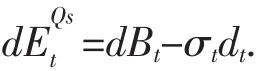
Xt在新测度下的表达式为：

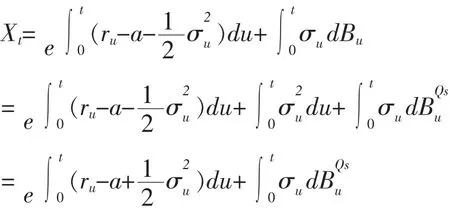
因此，我们考虑（4）和（5）中的关于死亡时间和WT两种期望得到：

由（3）和（6），我们得到：

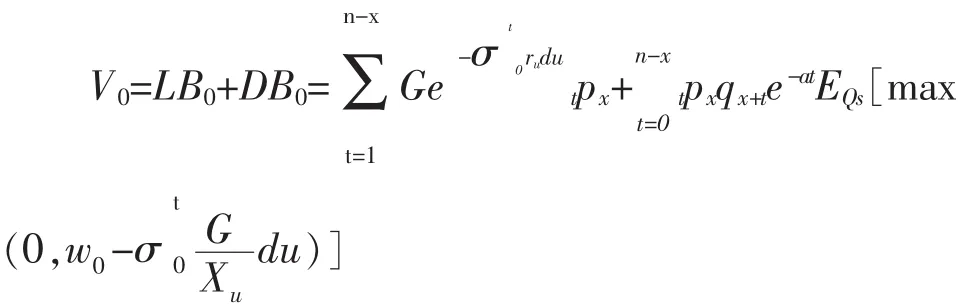
由公平原则，得：

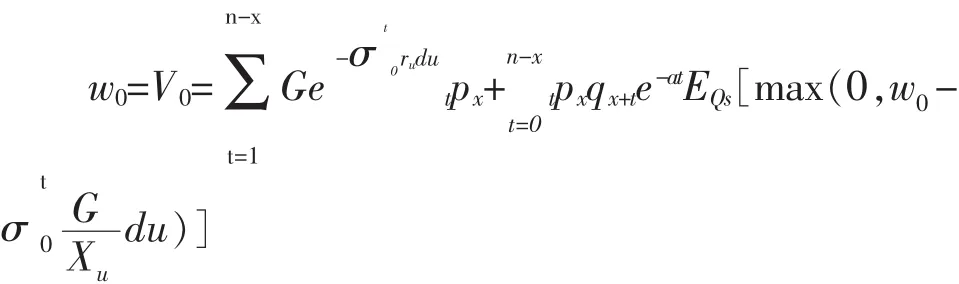
由上述方程可得到公平保证费用a。

显然，若保单持有人考虑动态策略，即不再以最低保证额度领取年金，则保险公司收取的费用应大于上述的费用a。

三、运用Regime-Switching模型对GLWB定价的模拟分析

下面我们利用Regime-Switching模型模拟变额年金的定价，并进行相关敏感分析。

假设表示时刻的金融市场的虚拟状态变量，且随机过程是Markov过程，且是一个半鞅。和分别表示市场状态为时的市场利率与波动率，且假设Xt表示t时刻的金融市场的虚拟状态变量，且随机过程｛X（t）:t≥ ｝0 是Markov过程，且是一个半鞅。rXt和σXt分别表示市场状态为Xt时的市场利率与波动率，且

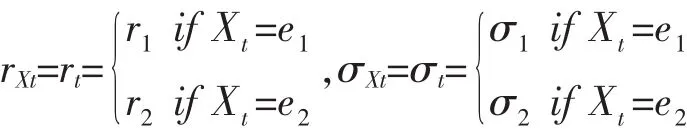
其中r1、r2和 σ1、σ2均为常数， 而且我们知道，在经济状态较好时市场利率大波动率小，经济状态差时正好相反，因此又有内在关系：r1≥r2、σ1≤σ2。根据刘迪（2011），假设经济状态转变时间间隔Δ＝1/12，马氏链的转移矩阵为：表示投保人的保证收益率。 根据 Gabriella、Piscopo（2012），保证收益率取g=0.05（美国变额年金市场投保人的保证收益率）。假设初始经济状态为X0=e1，则公平保证费用对利率和波动率的敏感性分析，如下表所示：

四、模拟分析

首先，假设保险公司设计的GLWB产品的销售对象是60岁的男性，令g=G w0

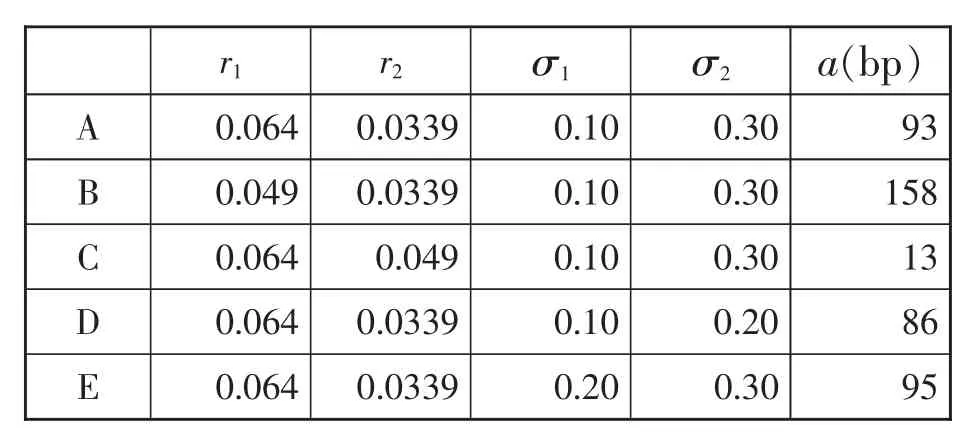
表1 公平保证费用对利率和波动率的敏感性分析

其中0.064为2009年的保险公司行业收益率，0.0339为2012年的保险公司行业收益率,0.049为两者的平均值。

由表1可以看出，当不变，增加50%时，公平保证费用减少86%。当不变，增加50%时，公平保证费用减少41%。因此，保证费随着利率的增加而减少，其中对公平保证费用的影响幅度更大。因此，为了获得充足保证费用、降低风险，保险公司对未来经济状态的变化需正确评估，采取合理的利率水平。同时，公平保证费用随着波动率的增加而增加，其中的影响更为显著。当保单持有人选择高风险资产投资时，变额年金账户余额不足，风险会增加，保险公司必须通过增加保费来保证最低利益的给付。

公平保证费用对Regime-switching模型的敏感性分析如表2所示：

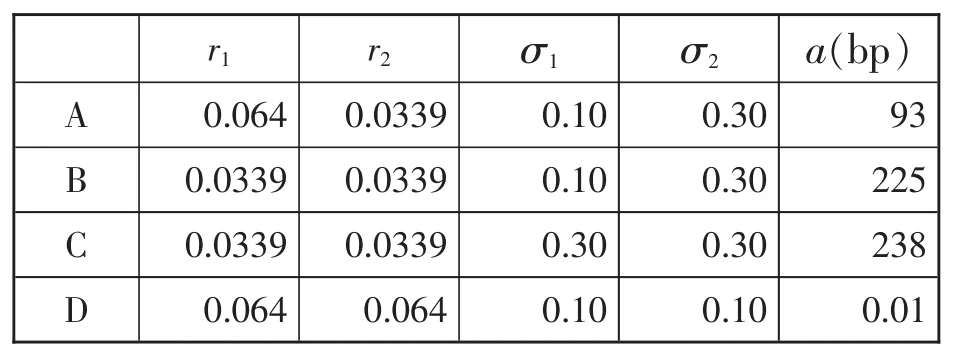
表2 Regime-switching模型的敏感性分析

从组合B与组合A的对比中可以发现：若采用Regime-switching考虑经济状态对利率的影响，考虑经济状态有向好的状态发展的可能，则公平保证费用由225降为93。采用Regime-switching考虑经济状态对利率和波动率的影响，则组合A与组合C的比较发现，不考虑经济状态向发展的可能，公平保证费用提高1.52倍。因此，考虑经济状态的转变对公平保证费用的影响，则保单持有人可享受经济状态好转带来的收益，缴纳的保证费用更加公平。由上表，可以看出经济状态转变对公平保证费用有较大影响。因此，保险公司在对GLWB产品进行定价时，要考虑经济变化带来的风险，正确评估所处的经济状态以及未来经济发展的趋势，得到更为公平的保证费用。

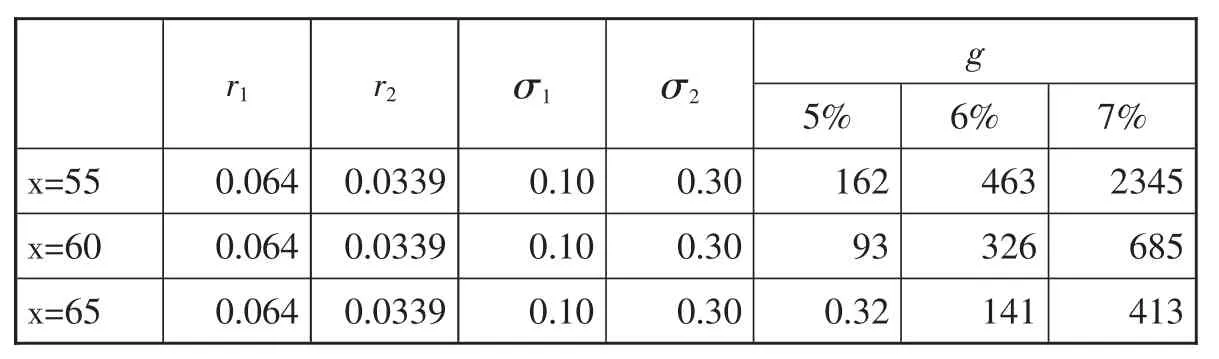
表3 不同取款率下对投保人初始年龄的敏感性分析

上表显示，若投保人初始领取年金年龄较低，则为了避免缴纳过高的保证费用，最低保证取款率不应过高。死亡率随着年龄的变化有着显著的变化，由于GLWB产品的领取时期较长，GLWB产品的公平保证费用对投保人初始领取年金年龄很敏感。表3显示，在取款率相等的情况下，保证费用随着投保人初始领取年金年龄的增加而减少。因此，为了降低费用，建议投保人推迟初始领取年金的年龄。若65岁以后开始领取年金，由于费用低廉，可以适当选择提高取款率，从而获得好的生活品质。因此，可建议保单持有人在6岁以后开始领取年金。

综上，年龄和死亡率对GLWB产品的公平保证费用影响严重。长寿风险对GLWB产品产生较大影响，保险公司在设计产品时避免死亡率预测失误，及时更新生命表，严格限制投保人初始领取年金的年龄，必要时需寻找合适的再保险来转移风险。

五、结论

随着人均寿命的增加和通货膨胀的加剧，长寿风险带来的影响越来越受到人们的关注，对于消费者来说，购买永久性年金可以有效地降低长寿风险。GLWB产品既可以转移长寿风险，还可以享受投资带来的收益，满足消费者的需求。本文对该类产品进行定价研究，改进了Gabriella Piscopo（2009）的定价模型，在模型中考虑经济状态的转变对公平保证费用的影响。对结果分析发现，利率和波动率等市场相关量的变动对GLWB产品的保证费用影响很大，因此，为了获得充足保证费用，保险公司要谨慎的对利率和波动率进行假设，采取合理的利率和波动率。对Regime-switching模型的敏感性分析得出，经济状态的变化给GLWB产品的保证费用有影响。保险公司为了降低经济状态转变带来的风险，在定价时需考虑经济状态变化，从而获得更为充足，公平的费用。同时，取款率和投保人领取年金的初始年龄对公平保证费用也有重大影响，尤其是年龄和死亡率对GLWB产品的公平保证费用影响严重。

综上，保险公司在设计GLWB产品时，尤其要考虑市场风险、长寿风险对保证费用的影响，采取合理的风险对冲方法，有效降低风险。

［1］Boyle P.P.,Schwartz E., （1977）.Equilibrium prices of guarantees under equity-linked contracts.The Journal of Risk and Insurance 44（2）,639-680.

［2］Bacinello,A.R.,Millossovich,P.,Olivieri,A.,Pitacco,E.,2011.Variable annuities:a unifying valuation approach［J］.Insurance:Mathematics and Economics,2011,49:285-297.

［3］Barbarin,Devolder.Risk measure and fair valuation of an investment guarantee in life insurance［J］.Insurance:Mathematics and Economics,2005,37:297–323.

［4］Bauer,Daniel,Kling,Alexander,RUSS,Jochen.A Universal Pricing Framework for Guaranteed Minimum Benefits in Variable［J］.ASTIN Bulletin,2008,38:621-651.

［5］Bélanger,A.C.,Forsyth,P.A.and Labahn,G,Valuing the Guaranteed Minimum Death Benefit Clause with Partial Withdrawals［J］.Applied Mathematical Finance,2009,16:451-496.

［6］Cheuk-Yin Nga,Johnny Siu-Hang Li,Valuing variable annuity guarantees with the multivariate Esscher transform ［J］.Insurance:Mathematics and Economics,2011,49:393-400.

［7］Chen Z.,Forsyth P.,（2008）.A numerical scheme for the im-pulse control formulation for pricing variable annuities with a Guaranteed Minimum Withdrawal Benefit.Numerische Mathematik109（4）,535-569.

［8］Chen Z.,Vetzal K.,Forsyth P.A.,（2008）.The effect of modeling parameters on the value of GMWB guaranteed.Insurance:Mathematics and Economics 43,165-173.

［9］Dai M.,Kwok Y.K.,Zong J.,（2008）.Guaranteed minimum withdrawal benefit in variable annuities.Mathematical Finance.

［10］Milevsky M.,Posner S.E.,（2001）.The Titanic Option:Valuation of the Guaranteed Minimum Death Benefit in Variable Annuities and Mutual Funds.The Journal of Risk and Insurance 68,1,91-126.

［11］Milevsky,M.A.,Salisbury,T.S.,Financial valuation of guaranteed minimum withdrawal benefits［J］.Insurance:Mathematics and Economics,2006,38:21-38.

［12］Gabriella Piscopo.The fair price of Guaranteed Lifelong Withdrawal Benefit option in Variable Annuity.Problems and Perspective in Management.Volume7,Issue4.

［13］刘迪.变额年金及最低利益保证的定价［D］.2011届研究生硕士学位论文.

［14］曾庆五.变额年金与变额寿险给付额的计算［J］.经济数学,1994,（1）.

［15］李冰清,廖朴.变额年金业务的风险度量与分析［J］.保险研究,2012,（4）.