原本不尽然,岂能想当然——对一道物理竞赛问题的深入研究

(南京师范大学附属中学江宁分校，江苏 南京 211102)

很多竞赛教程中都有这样的问题:

如图1所示,在铅直面内二平行导轨相距l=1cm,且与一纯电感线圈L,直流电源(E,r),水平金属棒AB联成一闭合回路.开始时,金属棒静止,之后无摩擦地自由下滑(不脱离轨道),设轨道足够长,其电阻可忽略,空间磁感应强度B的大小为0.4T.其方向垂直于轨道平面.已知电源电动势E=9V,内阻r=0.5Ω,金属棒质量m=1kg,其电阻R=1.1Ω,线圈自感系数L=12mH,试求金属棒最大下落速度.

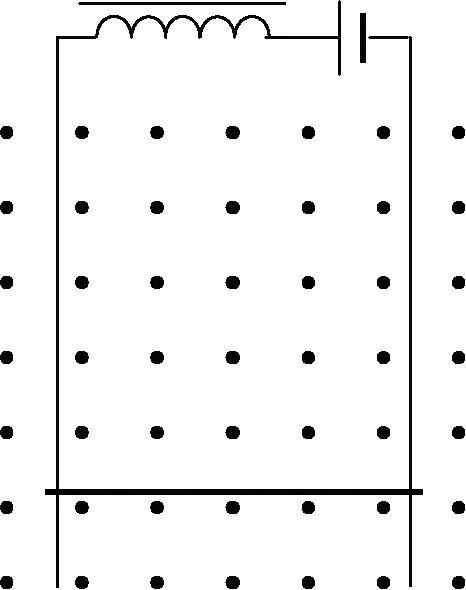
图1

原解法如下:

金属棒以任一速度v下落时,回路中感应电动势为εi,方向与E相反,回路中顺时针方向的电流为:

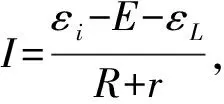
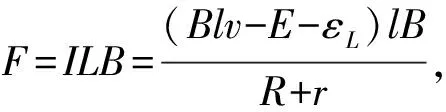
以上解法是一种想当然的解法.解题者显然认为，金属棒运动的速度是在不断地增大的，最后达到一个稳定状态,这时速度最大.但是,仔细推敲会发现,物体的运动情况不一定如此.

让我们先作定性研究,我们不妨假设电感的自感系数很大,棒在开始运动后的一段相当长的时间内，由于电感的作用,电流可以认为是零,棒作自由落体运动,当速度非常大后回路中才出现很小的电流,再假设回路的电阻很小,这时电流会慢慢变得非常大,从而又使棒作减速运动.可见，最终的速度不是最大速度.所以,出题者认为的运动模型是有问题的.

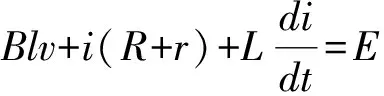
(1)

(2)

(3)

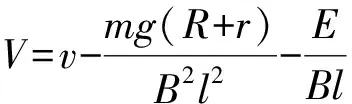
(4)

再由(3)式显然可得：

这是一个二阶常系数线性微分方程，其特征方程为：

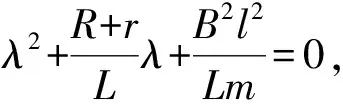
(5)

下面分几种情况加以研究：

代入(4)式可得：

(6)

其中C1,C2由下列初始条件决定：t=0时，v=0，v′=g，即由以下两式决定：

当m,R,r,B,l,L,E取适当值时，可以得到棒的v-t如图2所示.

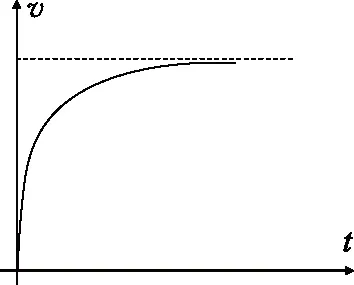
图2

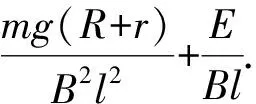
(7)

其中C1,C2由下列初始条件决定：t=0时，v=0，v′=g，即由下列两式决定:

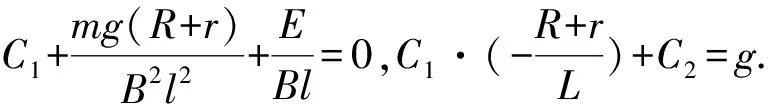
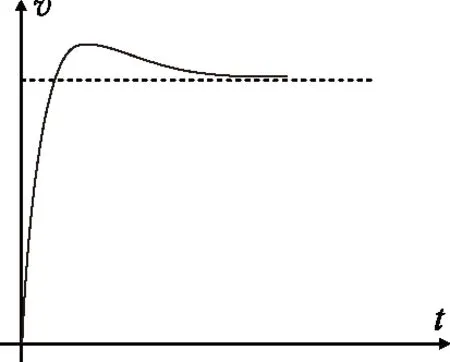
图2

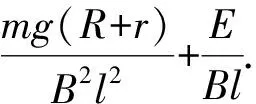
(8)

其中A,φ由下列初始条件决定：t=0时，v=0，v′=g，即由下列两式决定:

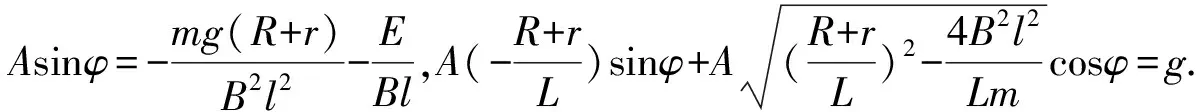
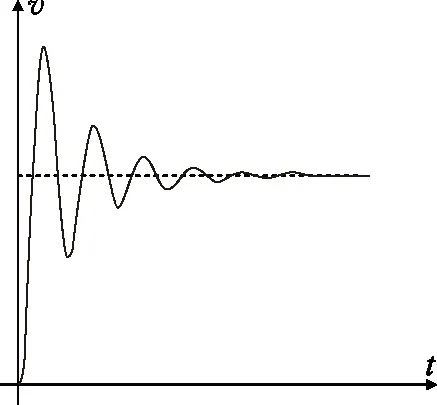
图2

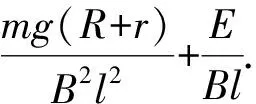
综上所述,原题所牵涉的运动模型是非常复杂的.具体的运动情况由m,R,r,B,l,E的具体值来决定.即使m,R,r,B,l,L,E数值给定,也应当进行定量分析并作分类讨论.由原题所提供的数据,代入(5)式计算可得Δ>0.也就是说,原题中小棒的运动情况正好就是上述图2所示的第一种情形.但是,目前的中学生是不可能作出这样的定量分析的.即使作为一道竞赛题,显然也是不妥的.