动生电磁感应中的典型问题探讨
(苏州市吴中区苏苑高级中学,江苏 苏州 215128)

图1
导体在磁场中垂直切割磁感线时,导体棒中的自由电荷与磁场发生了相对运动(如图1),从而自由电子在洛伦兹力的作用下向D点聚集,经过短时间的积累,D点聚集一定的负电荷,C点留下等量的正电荷,这样就在导体棒中形成了C高D低的电势差,即动生电动势ε.此时导体棒在垂直切割磁感线时可视为一个电源,此电源中的非静电力是由洛伦兹力充当的.当静电力与非静电力平衡时,自由电荷不再定向移动,即形成稳定的电动势.由qvB=qE=qε/L,即得ε=BLV.
切割类感应电动势产生的机理与化学电池产生电动势不同,这里的洛伦兹力的一个分力充当非静电场力,它的大小与是否有外电路无关.以下立足教科书,运用物理图景对电磁感应中切割类(即动生电动势)问题进行归纳与研讨.
1 匀强磁场中的动生电磁感应类问题
(1)导体棒平动切割磁感线
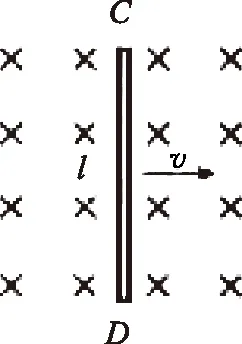
图2
如图2所示,此模型是动生电磁感应核心模型,其他问题是在此基础上衍生出来的,这也是历届高考对电磁感应知识模块考查的热点.若只是简单的记住公式,而不能理解动生电磁感应的产生机理是远远达不到高考要求的.
例题1(2011江苏卷) 如图3所示,水平面内有一平行金属导轨,导轨光滑且电阻不计.匀强磁场与导轨垂直.阻值为R的导体棒垂直于导轨静止放置,且与导轨接触.t=0时,将电键S由1掷到2,Q、i、v和a分别表示电容器所带的电荷量、棒中的电流、棒的速度和加速度.下列图像正确的是( ).
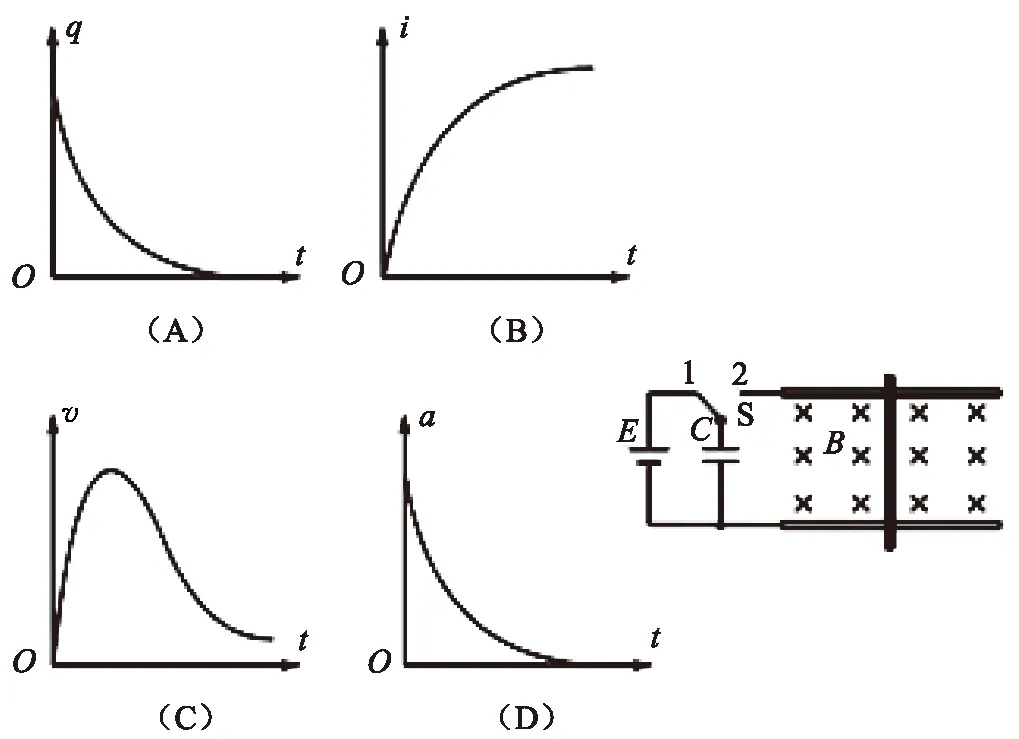
图3
本题涉及动生电磁感应、安培力、牛顿运动定律、动态电路以及电容器等知识点.考查学生综合能力,难度确实比较大,可以运用物理图景进行分析.

从动生电动势产生机制出发,不难看出导体棒中自由电荷随速度变化而变化只是充当“动态电源”的角色,最终整个系统趋于稳定,所以选D.
(2)导体棒(圆盘)转动切割磁感线

图4
图4中导体棒匀速转动切割磁感线,因为棒的每一点的线速度不同,所以产生的动生电动势并非BLV,由V=ωr并利用微元分析或利用平均速度易推得:


图5
图6

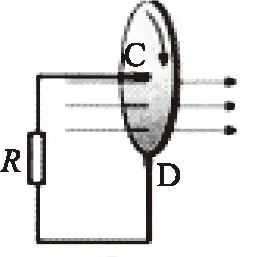
图7
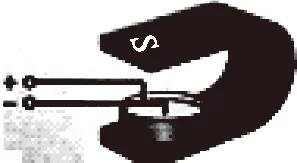
图9
(3)线圈平动切割磁感线
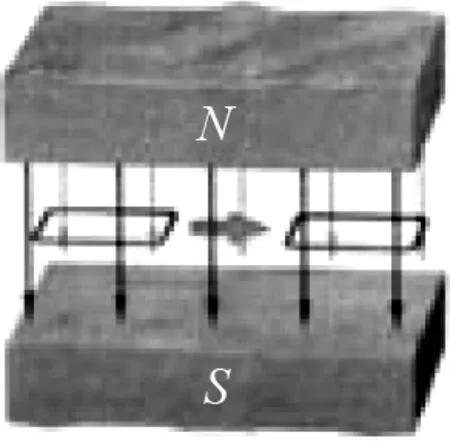
图10
如图10所示,由感应电流条件易推得:由于Δφ=0,所以闭合线圈内E(I)=0.但是如果仅仅从磁通量来理解线圈平动切割问题,在实际解题中可能会束手无措.
例题2 如图11所示,闭合铜环与闭合金属框相接触放在匀强磁场中,当铜环向右移动时(金属框不动)时,学生容易错误理解为:由于闭合铜环磁通量不变,从而铜环中没有感应电流.所以要抓住线圈平动切割的本质其实也是导体棒平动切割磁感线.图11中弧egf和弧ehf平动切割产生电动势相当于一个电源,其等效电路如图12所示,两电源并联对外电路供电.线圈abfgea感应电流是逆时针,而线圈dcfhed的感应电流是顺时针,且电流大小相等.
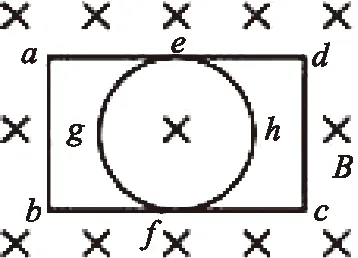
图11
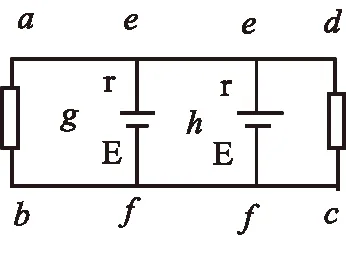
图12
学生往往会根据线圈中磁通量变化与否来判断感应电动势的有无,这的确很方便,但这仅是一个表面的结论.这里线圈多局限于一个独立的线圈,而对于本题所涉及到多个回路,我们仍需抓住产生感应电动势的源头:(部分)导体棒切割磁感线.
(4)线圈转动切割磁感线
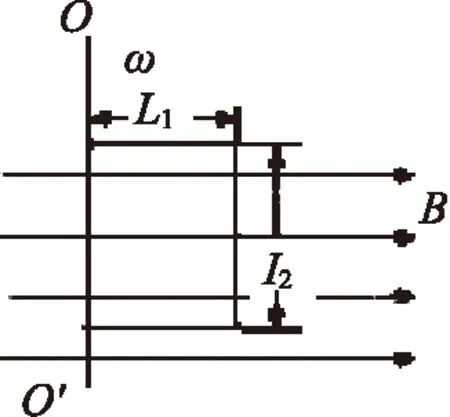
图13
线圈转动切割在教材中所占比重较大,交流电一章都是围绕此模型进行讲解的,这也是由导体棒切割模型所衍生的.图13中仅仅是导体棒L2充当电源,只是由于导体棒运动而产生的电动势按正弦规律变化而已,即e=NBSωsinωt.对于线圈转动切割磁感线,如果只是肤浅的记住感应电动势的公式,显然是不够的.
例题3 如图14所示,导体棒PQ在外力作用下沿竖直光滑的圆弧轨道以角速度ω匀速转动,线圈每边长a匝数为n,线圈总电阻为r.整个装置处在磁感应强度B的匀强磁场中,求电阻R上的电流.
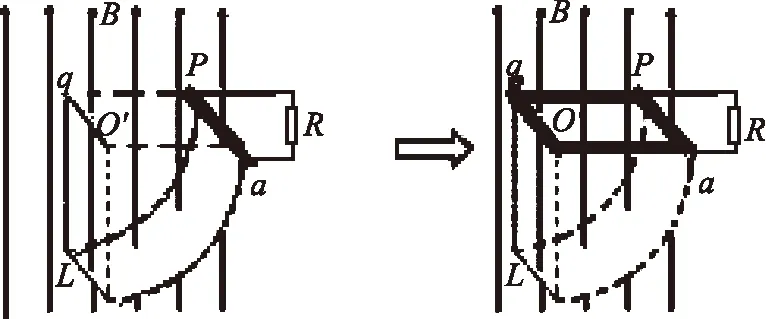
图14 图15
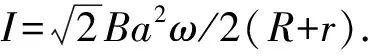

图16
(5)线圈变形切割磁感线
可以从磁通量变化角度容易理解线圈变形切割磁感线产生电动势,其实质也是每一部分导体棒切割磁感线(如图16).教科书中也涉及到此模型的应用,例如动圈式扬声器(图17)工作原理:声音使纸盒震动,线圈将随纸盒震动,线圈切割磁感线,产生感应电流.
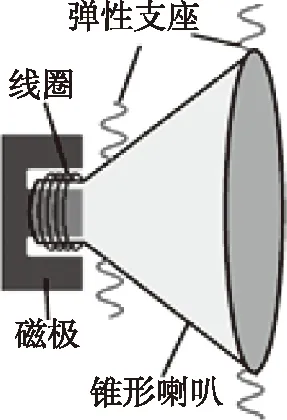
图17
2 非匀强磁场中的动生电磁感应类问题
(1)在辐向磁场中切割磁感线
教科书中在介绍磁电式电流计时,出现了辐向磁场(如图18).线圈转动时与在匀强磁场中情况不同,并非产生正弦或余弦的电动势.这里其实也是导体棒切割磁感线,且处处垂直切割.由于每个位置磁感应强度大小相同,所以产生的是恒定的电动势.
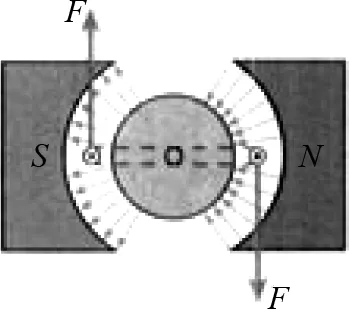
图18
例题4(2012江苏卷) 某兴趣小组设计了一种发电装置,如图19所示.在磁极和圆柱状铁芯之间形成的两磁场区域的圆心角均为α,磁场均沿半径方向,匝数为N的矩形线圈abcd,其边长ab=cd=l、bc=ad=2l,线圈以角速度ω绕中心轴匀速转动,在磁场中,两条边所经过处的磁感应强度大小均为B、方向始终与两边的运动方向垂直.求线圈切割磁感线时感应电动势的大小Em.
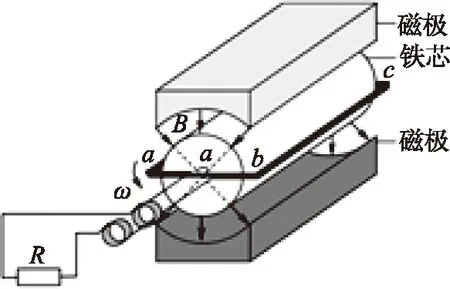
图19
抓住“电源”其实是由bc、ad两边垂直切割产生的,且为恒定电源,两电源串联,易得Em=2NBl2ω.
(2)在条形磁铁产生的磁场中切割磁感线
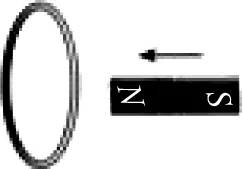
图20
如图20所示,由于条形磁铁周围磁场分布不均,线圈中磁通量发生变化,从而在闭合线圈中产生电动势,其大小可通过法拉第电磁感应定律Em=nΔφ/Δt来求.
例题5 若在圆环上下两点连入一电阻(如图21),环中有电流吗?

图21
如果仍从磁通量变化角度来处理,会得到与上述一致的答案.但是如果从产生电动势的实质来看,显然这样的理解是错误的.因为当条形磁铁靠近圆环时,这里的线圈的每一部分与磁场发生了相对运动,导线环中的自由电子在洛伦兹力的作用下定向移动形成电势差.如果将圆环中两点接入一电阻,相当于将圆环分成两部分,每一部分均切割磁场,产生两个并联的“电源”.
综上所述,切割类问题虽然类型很多,但实质上均为导体棒切割磁感线产生动生电动势,其中切割部分相当于一个电源.解决此类问题关键是找出电源部分,然后画出等效电路图,把抽象的电磁感应问题转化为学生熟悉的电路问题.
参考文献:
[1]人民教育出版社,课程教材研究所,物理课程教材研究开发中心.普通高中课程标准实验教科书 物理选修3-1、3-2[M].北京:人民教育出版社,2004.
[2]江苏省教育考试院.2014年江苏省普通高中学业水平测试(选修学科目)说明[M].南京:江苏教育出版社,2014.

