两个实对称矩阵可同时合同对角化的条件

罗高骏,周 良

(湖北师范学院 数学与统计学院， 湖北 黄石 435002)

两个实对称矩阵可同时合同对角化的条件

罗高骏,周 良

(湖北师范学院 数学与统计学院， 湖北 黄石 435002)

矩阵对角化是高等代数研究的重要课题之一。对于一个矩阵对角化的问题, 许多文章已得到了很好的结果。给出了一系列两个实对称矩阵可同时合同对角化的充分和充要条件。

实对称矩阵；同时合同对角化；对角矩阵

1 引言与引理

如果矩阵A和它的转置矩阵A′相等，那么就称A为对称矩阵。

对于数域P上的两个n级方阵A，B，如果存在数域P上的n级可逆方阵C，使得B=C′AC，那么称A合同于B.

可对角化矩阵是线性代数和矩阵论中重要的一类矩阵，可对角化矩阵在线性代数中有重要的应用，因为对角矩阵特别容易处理: 它们的特征值和特征向量是已知的，并通过简单的提升对角元素到同样的幂来把一个矩阵提升为它的幂。

数域P上的任意一个对称矩阵都合同于一对角矩阵(参看[1]第五章的定理2)。

对于数域P上的两个n级方阵A，B，如果存在数域P上的n级可逆方阵C，使得C′AC和C′BC都是对角矩阵，那么称A与B可同时合同对角化。

许以超先生在[3]的第十五章的定理4指出：两个n级实对称方阵A，B构成的λ- 矩阵A+λB合同于一个分块对角矩阵，其中的对角块由 以及五种标准块构成(参见[3])。

由于对角矩阵是最简单的分块对角矩阵，因此本文研究两个n级实对称方阵在什么条件下可同时合同对角化？

关于实数域上的两个n级对称方阵A，B，能够同时合同对角化的充分条件，众所周知的有两个:

引理1[2]设A，B都是n级实对称方阵,如果AB=BA，那么存在一个n级正交矩阵T，使得T′AT和T′BT都是对角矩阵。

引理2[2]设A是n级正定方阵，B是n级实对称方阵，那么存在一个的n级实可逆方阵C，使得C′AC和C′BC都是对角矩阵。

文献[6]中的推论5指出：设A，B都为n级半正定实对称阵，则存在实可逆方阵C，使得C′AC和C′BC都是对角矩阵。

本文更深入地研究了实数域上两个n级实对称方阵可同时合同对角化的充分和充分必要条件。

2 主要结果

定理1[4]设A，B为n级实对称方阵, 则A，B可同时合同对角化的充要条件是存在n级正定的实对称方阵H, 使得AHB=BHA.

证明 “⟹ ” 设A，B可同时合同对角化，则存在n级实可逆方阵P，使得P′AP，P′BP为对角矩阵，故P′APP′BP=P′BPP′AP，所以APP′B=BPP′A，即存在n级正定的实对称方阵H=PP′, 使得AHB=BHA.

“⟸ ” 设H为正定矩阵，则有可逆方阵P，使得H=PP′ .由APP′B=BPP′A，可得，

P′APP′BP=P′BPP′AP

而P′AP,P′BP为对称矩阵且相乘可交换，故由引理1，可得P′AP，P′BP可同时合同对角化，所以，A,B可同时合同对角化。

定理2 设A，B为n级实对称方阵,且A可逆，则A，B可同时合同对角化的充要条件是A-1B可相似对角化。

证明 “⟹ ”设A，B可同时合同对角化，则存在n级实可逆方阵P，使得P′AP=Λ，P′BP=∑，Λ,Σ为n级对角矩阵。所以P-1A-1BP=Λ-1∑ ，即A-1B可相似对角化。

“⟸ ” 设A-1B可相似对角化，即存在n级实可逆方阵C=(r1,r2,…rn),ri∈n以及对角矩阵∑=diag(λ1,λ2,…λn)，λi∈,使得C-1A-1BC=∑，即BC=AC∑且C′BC=C′AC∑ .

又假定相同的λi是排放在一起的，因而可设∑ 有如下形式

∑=diag(∑1,∑2,…∑k) ∑i=λiI,i=1,2,…,k且λ1,λ2,…,λk互不相同

如果你说中国不好，你就是西奴；如果你说美国好，你就是美狗；如果你要中国向美国学习你就是五美分；如果你说不想做中国人，就是十恶不赦的汉奸。但如果你什么都不说，悄悄把中国籍变成美国籍，你就是成功人士；如果你拿绿卡在美国街头高喊“我爱你中国”，你就是令人敬佩的爱国主义者。——橘少Colin

选取适合1≤i,j≤k的任意i,j使λi≠λj，并考察恒等式C′BC=C′AC∑两边的i,j元。这就是

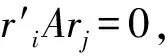
C′BC=diag(B1,B2…Bk)=C′AC∑=diag(λ1A1,λ2A2…λkAk)

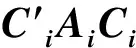
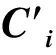
令D=diag(C1,C2…Ck) ,Λ=diag(Λ1,Λ2,…Λk)则D是n级可逆方阵，Λ是对角矩阵，且D′C′BCD=∑Λ，D′C′ACD=Λ.即A，B可同时合同对角化。

推论1 设A，B为 级实对称方阵,且B可逆，B-1A有n个互异的特征根，那么A，B可同时合同对角化。

证明 由B-1A有n个互异的特征根可知B-1A可相似对角化，所以由定理2可得A，B可同时合同对角化。

推论2 设A，B为n级不可逆的实对称方阵，且存在λ0∈使得A+λ0B可逆，则A，B可同时合同对角化的充要条件是 (A+λ0B)-1B可相似对角化。

定理3[6]设A，B都为n级半正定实对称阵，则存在n级实可逆矩阵C，使得C′AC和C′BC都是对角矩阵。

推论3 设A，B都为n级实对称阵，且 0≤rank(A)，rank(B)≤1,那么A，B可同时合同对角化。

证明 由于0≤rank(A),rank(B)≤ 1，所以A，B为半正定矩阵，或者-A，B为半正定矩阵，或者A，-B为半正定矩阵，或者-A，-B为半正定矩阵，由定理5可知A,B可同时合同对角化。

推论4 设A，B都为n级实对称阵，且对任何μ,v>0,μI+A,vI+B正定，那么A，B可同时合同对角化。

证明 由μI+A正定可得，μI+A的特征值μ+λi≥0 (λi为A的任意特征值)。由于μ为任意正数，故λi一定大于等于0,所以A是半正定的。同理B也是半正定的。由定理3可知 ，A,B可同时合同对角化。

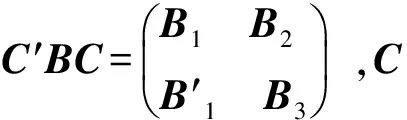
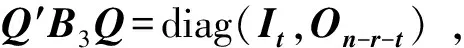
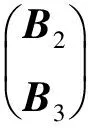
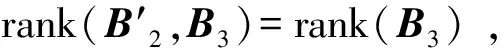
通过引理3，我们可以考虑，如果将定理3中的条件减弱，那么A，B是否仍然可同时合同对角化？

定理4 设A为n级实半正定对称方阵，B为n级实对称方阵，记

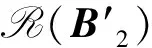
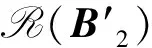
因为B1-XB3X′ ，B3都是对称矩阵，故分别存在r级实正交矩阵E和n-r级可逆实方阵F，使得

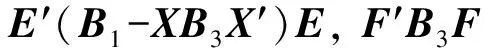
所以D′C′ACD,D′C′BCD为对角矩阵，即A，B可同时合同对角化。

定理5 设A，B都为n级实对称阵，则A，B可同时合同对角化的充要条件是存在n的一组基{μ1,μ2,…μn} 使得μiA,μiB在上线性相关(i=1,2,…n) .

证明 “⟹ ”因为A，B可同时合同对角化，故存在n的一组基{μ1,μ2,…,μn} 使得.当时，则存在可逆阵使得μiAC′=0，从而μiA=0，同理当时，有μiB=0，这样μiA,μiB在上线性相关。当不全为0 时，因为故

即μiA,μiB在上线性相关(i=1,2,…,n) .

αiμiA+βiμiB=0(i=1,2,…,n)

在集合X={μ1,μ2,…μn} 中，定义关系“～”， 如果αiβj-αjβi=0 ，则μi～μj.

下证该关系为等价关系:

显然该关系满足自反和对称，设μi～μj，μj～μk，则

αiβj-αjβi=0,αjβi-αkβj=0

(1)

由上式可得αiβkαjβj=αkβiαjβj，当αjβj≠0 时，μi～μk，当αj,βj有一个为0 时，假设αj=0，则βj≠0，由(1)可得αi=αk=0，即αiβk-αkβi=0，所以μi～μk，同理αj≠0，则βj=0，μi～μk.所以该关系满足传递性，综上所述关系“ ～”是一个等价关系。那么可设X=X1∪X2∪…∪Xm是集合X的一个划分。

因为Xk(k=1,2,…,m)中μi其对应的αi,βi和μk(i≠j) 其对应的αj,βj有αiβj=αjβi，所以(αi,βi)=

l(αj,βj),l∈.故每一个μi∈Xk其对应的αi,βi，均可用αk,βk表示(k=1,2,…,m) .

所以存在αk,βk∈且αk,βk不全为0，使得

αkμA+βkμB=0,∀μ∈Xk

(2)

同理也有αlvA+βlvB=0,∀v∈Xl.

由αkβl-αlβk≠0，k,l=1,2,…,m和 (μAv′)′=vAμ′，可得

μ′Av′=μBv′=0,μ∈Xk,v∈Xl

(3)

不失一般性，设μ1,μ2,…,μn1∈X1,μn1+1,μ2,…,μn1+n2∈X2,……,μn1+n2+…+nm-1+1…,μn∈Xm， 设矩阵C且矩阵C的第i行为μi，矩阵C是可逆矩阵，由(3)可得

CAC′=diag(A1,A2,…,Am)

CBC′=diag(B1,B2,…,Bm)

其中Ak,Bk都是nk级实对称矩阵(k=1,2,…,m)，由(2)可得，

αkμAη′+βkμBη′=0,μ,η∈Xk.

所以αkAk+βkBk=0，k=1,2,…,m,而αk,βk不全为 0，故Ak,Bk可同时合同对角化，所以，A,B可同时合同对角化。

[1]北京大学数学系几何与代数教研室代数小组. 高等代数(第二版) [M]. 北京:高等教育出版社,1988.

[2]夏 璇.二个矩阵同时对角化[J].南昌航空工业学院学报(自然科学版)，2003,17(3)：26～32.

[3]许以超. 代数学引论[M].上海：上海科技出版社,1965.

[4]叶年武.实数方阵的同时对角化[J].北京工业大学学报，1991,17(4):92～95.

[5]Horn.Matrix Analysis[M].Cambridge:Cambridge University Press,1985.

[6]周立仁.矩阵同时对角化的条件讨论[J].湖南理工学院学报(自然科学版)，2007,20(1)：8～10.

Theconditionsforsimultaneouslycongruentdiagonalizationoftworealsymmetricmatrices

LUO Gao-jun, ZHOU Liang

(College of Mathematics and Statistics, Hubei Normal University,Huangshi 435002,China)

The diagonalization of matrices is one of the important topic in the field of advanced algebra. For the diagonalization of a matrix, many articles have got good results.This paper gives a series of sufficient and necessary conditions and sufficient conditions for simultaneously congruent diagonalization of two real symmetric matrices.

real symmetric matrix; simultaneously congruent diagonalization; diagonalizable matrix

2013—11—26

罗高骏(1990— )，男，湖北黄石人，硕士研究生，主要研究方向为矩阵分析.

O151.21

A

1009-2714(2014)02- 0061- 04

10.3969/j.issn.1009-2714.2014.02.014