一类食饵依赖型捕食-食饵系统的稳定性分析与最优捕获
陈 静,李必文,刘唯一,刘细宪,柯于胜
(湖北师范学院 数学与统计学院, 湖北 黄石 435002)
一类食饵依赖型捕食-食饵系统的稳定性分析与最优捕获
陈 静,李必文,刘唯一,刘细宪,柯于胜
(湖北师范学院 数学与统计学院, 湖北 黄石 435002)
首先建立了一类食饵依赖型捕食-食饵生态经济模型,并对该模型的生物经济学涵义作了简要说明;接下来运用Routhchurwitz判据对系统平衡点的局部稳定性进行了详细分析,得到了该系统正平衡点的局部稳定性判据;最后通过动力学分析得到了食饵种群持久生存前提下的最大持续收获量,同时探究了该前提下价格随供求变化的经济效益的最大值.
捕食-食饵模型;食饵依赖;生态经济;价格随供求变化;局部稳定性;最优捕获
0 引言
在人类有限度的捕获下,可再生资源一般具有一定的自我恢复能力.然而,由于一味地追求高产出高效益,人类在发展社会经济的过程中对可再生资源进行过度地开发利用,导致可再生资源日趋枯竭,破坏了赖以生存的生态环境,制约着社会、经济的发展.人类应该在持续稳产的大前提下适度开发再生资源,以维持生物种群的长久持续生存为基础追求最高产量或最优的经济效益.
本文着手研究了一类食饵具有Logistic增长率的价格随供求变化的捕食-食饵系统稳定性与最优捕获. 我们的模型建立于文献[2]的捕食-食饵系统,如下:

(1)
其中x,y分别表示食饵和捕食者的密度,a,r,k都是正常数,E为捕捞努力量.
为了更贴近实际,捕食者与食饵之间的相互作用可以用一个与食饵数量相关的功能函数来描述:
(2)
1 模型解释
对于系统(2),令
则F1(μ,X) 、F2(μ,X) 分别表示食饵种群、捕食者种群的增长率,从而我们可以得到以下结论:
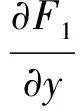

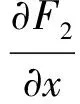

2 平衡点的局部稳定性
易计算得系统(2)存在唯一的平衡点:
(3)
从生物经济学角度出发,为使得食饵、捕食者、捕获强度都有意义,我们只考虑该系统的正平衡点,故而此处a-bβ>0,r-E-kx0>0.
系统(2)在正平衡点处的雅可比矩阵为
特征方程:
λ2+a1(μ)λ+a2(μ)=0
(4)
其中



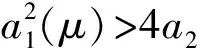







从而可得出如下定理.
定理 (平衡点的局部稳定性)
i) 当捕捞强度E 满足:



ii)当捕捞强度E 满足:



3 最优捕获问题
3.1持续产量
首先我们来关注上述定理的生物经济学解释:



3.2最大持续收获量的捕捞策略


3.3价格随供求变化的经济效益最大化
1954年,Gordon在文献[6]中提出了这样的经济理论:
净利润 (NER) =总收入 (TR) - 总成本 (TC)
记利润为v,捕获努力量为E,单位捕获量的价格为p,单位捕获量所投入的实际成本为c,总产量记为Y(E),则总收入为TR=pY(E),总成本是TC=cE,从而有
v=pY(E)-cE
(5)
我们都知道,在市场经济中商品的价格与市场供求量息息相关. 对此,在商品需求量固定不变的假设下,范猛等学者提出了更加符合实际的价格函数([文献5]):



(6)
结合(5)式与(6)式,我们可以这样定义利润:

(7)



此时的最大可持续净收益:

[1]王 静,王 克.具有年龄结构的单种群模型单一捕获的优化问题[J]. 东北师大学报(自然科学版),2013,35(2):1~6.
[2]陈伯山,廖晓昕.微分代数系统的标准型和分支 [J].应用数学学报,2000,23(3):429~443.
[3]Anderson L G. Optimun economic yield of a fishery given a variable price of output [J]. Journal of the Fisheries Research Board of Canada ,1973,30:509~518.
[4]Dong L Z,Chen L S,Sun L H. Optimal harvesting Policies for Periodic GomPertz systems [J]. Nonlinear Analysis: Real World Applications,2007,8(2): 572~578.
[5]范 猛,王 克.价格随供求变化的捕获问题[J]. 生物数学学报,2001,16(4):411~415.
[6]Lu Z,Chi X,Chen L. Impulsive control strategies in biological control of pedticide [J]. Theoretical Population Biology,2003,64(1):39~47.
[7]Wang L,Liu Z. Impulsive diffusion in single species model [J]. Chaos,Solitions& Fractals,2007,33(4):1213~121.
[8]Wang J,Wang K. Optimal control of harvesting for single population[J]. Applied Mathematics and Computation,2004,156(1):235~247.
[9]Gaines E,Mawhin J L.Coineidence Degree and Nonlinear Differential Equations[J]. Berlin:Springer,1997.
[10]Zhang X Y,Shuai Z S,Wang K. Optimal impulsive harvesting policy for single population[J]. Nonlinear Analysis: Real World Applications,2003,4(4):639~651.
[11]王 克. 捕食者-食饵系统持久的充要条件及其分枝[J]. 生物数学学报,1995,102:49~53.
[12]马知恩. 种群生态学的数学建模与研究[M]. 合肥:安徽教育出版社,1996.
[13]廖晓昕. 稳定性的数学理论及应用[M].武汉:华中师范大学出版社,2006.
[14]陈兰荪. 数学生态学模型与研究方法[M]. 北京:科学出版社,1988.
[15]王朝珠,秦化淑,最优控制理论[M]. 北京:科学出版社,2003.
StabilityanalysisandoptimalharvestofAprey-dependentpredator-preybiologicaleconomicsystem
CHEN Jing,LI Bi-wen,LIU Wei-yi,LIU Xi-xian,KE Yu-sheng
(College of Mathematical and Statistics,Hubei Normal University,Huangshi 435002,China)
In this paper,an economic harvesting model of prey-dependent is established. After a bio-economic explanation of the model,we analyze the local stability of positive equilibrium point in detail by routhchurwitz criterion,and naturally get the criteria for local stability. Maximum sustainable yield is given through dynamics analysis when the permanence of prey is guaranteed. Similarly,the revenue with price changed with demand and supply is studied and the maximum revenue is presented.
predator-prey model; prey-dependent; biological economic; price changed with demand and supply; local stability; optimal harvesting
2013—12—15
陈静(1987— ),女,湖北黄冈人,硕士研究生,主要研究方向为微分方程与控制论.
O175.14
A
1009-2714(2014)02- 0035-05
10.3969/j.issn.1009-2714.2014.02.009

