基于调用环境树的软件度量研究

王凤琴

(湖北师范学院 物理与电子科学学院， 湖北 黄石 435002)

基于调用环境树的软件度量研究

王凤琴

(湖北师范学院 物理与电子科学学院， 湖北 黄石 435002)

通过对调用环境树的扩展，并针对方法的类内和类间度量，在提出新的度量公式的基础上，证明了相关的度量可行性需满足的性质。

调用环境树;方法度量;软件度量

0 前言

软件度量是一个研究非常活跃的领域。Stevens提出了面向过程开发领域中的聚合，指出聚合为一个模块的元素属于另外一个模块的度量值。Eder[1]提供了一个以高聚合为目标的框架，并提出了可理解的面向对象系统的聚合标准。他们采用已有的基于过程的和基于对象的度量框架，区分了面向对象的三种类型聚合：方法，类和继承聚合。Chidamber和Kemerer[2，3]定义相似为共同的属性集合，并以此来定义类的聚合为它的方法的相似度。方法集合M的相似度是所有属性中的共同被使用的属性的数量。

1 基于扩展调用环境树的方法聚合度量

Atanas Rountev[4]认为调用环境树是方法体中方法互相调用的上下文。本文在此基础上进行了扩展：1)增加“方法的所属类”关系进而对类进行相关度量；2)扩展注释信息以加强程序理解；3)增加方法调用线性链以进行更精确的度量。扩展调用环境树考虑系统中类的方法之间的消息传递关系，是一种可以加强程序理解的可视化图形。它既显现出同一个类中方法之间的调用关系，也显现出不同类的方法之间的调用。扩展调用环境树的形式定义：

定义1 扩展调用环境树是一个带根星型总线图G=(root,V，E，Order).其中：root是系统的入口方法。V表示结点集合。V=(header，comment)，结点包括头信息header和注释comment.头信息中定义了消息传递格式style.E表示边的集合，可以看作调用方和被调用方的偏序关系，E=，callout表示调用结点，callin表示被调用结点。Order是一个简单的整数，表示一个非叶子结点中的调用顺序。

定义2 header=style1∨style2∨style3∨style4。 “∨ ”表示析取关系。style1=方法名M(参数列表) in 类对象名C，表示类C中的结点所表示的方法/模块M.style2=方法名M(参数列表) in style1.Style3=方法名M(参数列表) in 类对象名C：对象名V；表示赋值语句。sytle4=style3 of[返回类型]，返回类型是style3中的对象名V的返回类型。

定义3 总线结构，有两种情况采用总线结构，第一种情况是共享数据依赖，两个方法中引用相同的参数或者全局变量。第二种情况是方法调用依赖。记为:DirectlylineStructure(V)表示直接相连方法链，结点在整个系统中引出的线性结构记为lineStructure(V).显然DirectlylineStructure(V) ⊆lineStructure(V).

定义4 星型结构：星型和总线是图的拓扑结构，是方法的无相关调用关系。记为：starStructure(V).

定义5 类内链出度数:∀vi∈V,vi∈linStructure.V记number(ei|vi→vi+1)(inClass)表示在结点vi所引出的链中直接关联并在同一个类中的结点连接的边的个数。

定义6 类内出度数:∀vi∈V，记number( ei|vi→vi+1)(DirectlyinClass)表示结点vi所引出的边中两个在同一个类中的结点直接连接的边的个数。

定义7 类外出度数:∀vi∈V，记number(ei|vi→vi+1)(DirectlyoutClass)表示结点vi所引出的边中两个不在同一个类中的结点直接连接的边的个数。

定义8 结点链层数:

|lineStructure|(layer)=number(ei|vi→vi+1)(inClass)+number(ei|vi→vi+1)(outClass)

定义9 相关节点个数:链上所有节点之和|M|，在图中显示为从特定节点所能到达的所有节点之和。为|M|=number(ei：callout):(vi)+|lineStructure|(layer)

定义10 度量公式:

类内直接连接方法的相对数(类内紧密类内聚度):

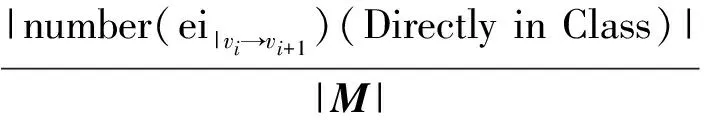
类内直接或者间接连接方法的相对数(类内松散类内聚度):

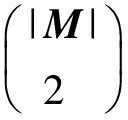
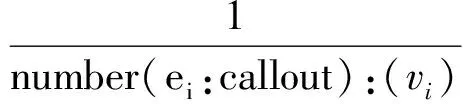
类间直接连接方法的相对数(类间紧密类内聚度):

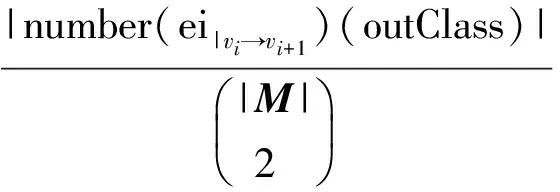
类间直接或者间接连接方法的相对数(类间松散类内聚度):

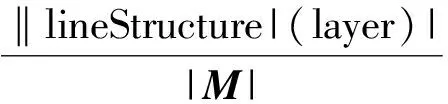
2 相关性质证明

本节中给出在文献[5]中所描述的聚合度量应该满足的性质(非负和正规性，空值和最大值，单调性，无关结点联合)的证明。

性质1 非负和正规性:度量值都在[0.0..1.0]区间范围之内。

证明 从度量公式中可以看出，公式的分子小于分母，因此，此结论成立。

性质2 空值和最大值:如果关联为空，聚合值为0，最大关联时聚合值为最大。

证明 没有关联，度量值为0(根据聚合公式)。当所有的关联都表示要度量的聚合时，聚合值为最大，值为1.

下面的x表示对应公式分子，y表示对应公式的分母，z表示引出的线性个数。

性质3 单调性:从一个类中，移除关联应该比没有移去之前更少类内聚合。

性质4 单调性:增加关联后比没有增加关联之前更多的聚合。

性质5 无关结点联合:合并无关结点后，得到的聚合度量值不会增加。

证明 采用数学归纳法，只需证明合并两个结点的情况。再使用穷举法，分为下列几种情况：第一是当合并的结点都为叶子结点时，由于合并前后的度量值都为0，也就是说合并后的聚合度量值没有增加；第二种情况时合并的结点都为孤立结点，合并前后的度量值也为0；第三种情况是合并的结点之一为叶子结点或者为孤立结点，由于叶子结点和孤立结点没有分支，度量的结果为非叶子结点的度量值；第四种情况是合并的结点都是非叶子结点，此时也就证明如下不等式：

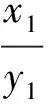
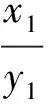
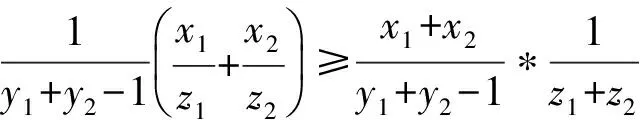
注意：上面的不等式同时取等号的情况是：y1≥1∧y2≥1 ∧(z1=0∨z2=0)这是由于分母不为0，因此就不能取等号。取等号的情况是上面讨论的三种情况。

性质6 两个类或者方法除非完全相同，采用相同的度量产生的度量值可能相同。

证明 有两种情况：第一种情况是：由于本文的度量是基于方法间的消息传递而产生的调用环境图，如果由两个结点产生的图形是同态的，也就是说，这两个结点的消息传递关系在数值上会产生相同的值。从而会产生相同的值，但是这也可以说：它们之间有相同的聚合/耦合度量。第二种情况是：考察的两个结点的度量公式的分子分母的比值相同，此时应该借助经验系统来判断。

性质7 对于关联的重新排列，紧密类聚合不变。

证明 边的计数是决定什么测量，边的数值没有变化，由度量公式可以看出，此结论是正确的。

性质8LCC对应的关系是相应于TCC对应的关系的传递闭包(LCCic和LCCoc相应，TCCoc和TCCic相应)。

证明 设(mi,mj) 和(mj,mk) 是类内直接调用关系，由图的出度和入度可以看出(mi,mk) 也存在于类内间接调用关系的集合中。因此，由传递闭包的定义，LCCic是相应于TCCic的传递闭包；同理可以证明：LCCoc是相应于TCCoc的传递闭包。

3 实例

图1是一个简单的程序产生的调用环境图和相应的度量值，限于篇幅关系，本节略去了相应的程序。从表1中可以看出：h1()的TCCic>TCCoc，且LCCic>LCCoc,h1()中很好的满足面向对象的高聚合特性，因为h1()中调用的方法基本上和h1()同属相同的类里。但是对于g2()方法，其TCCicTCCoc,它存在某些坏味道，需要进行重构，因为g2基本上只是调用了其它类的方法，它更适合放到其它类里面。

4 总结与展望

本文分析了当前在逆向工程领域和聚合度量领域的研究现状，对方法度量提出了新的度量公式，但是存在如下问题未解决1)没有进行方法交互的分类；2)方法交互的潜在线性相关关系，这将作为本文的后期工作。

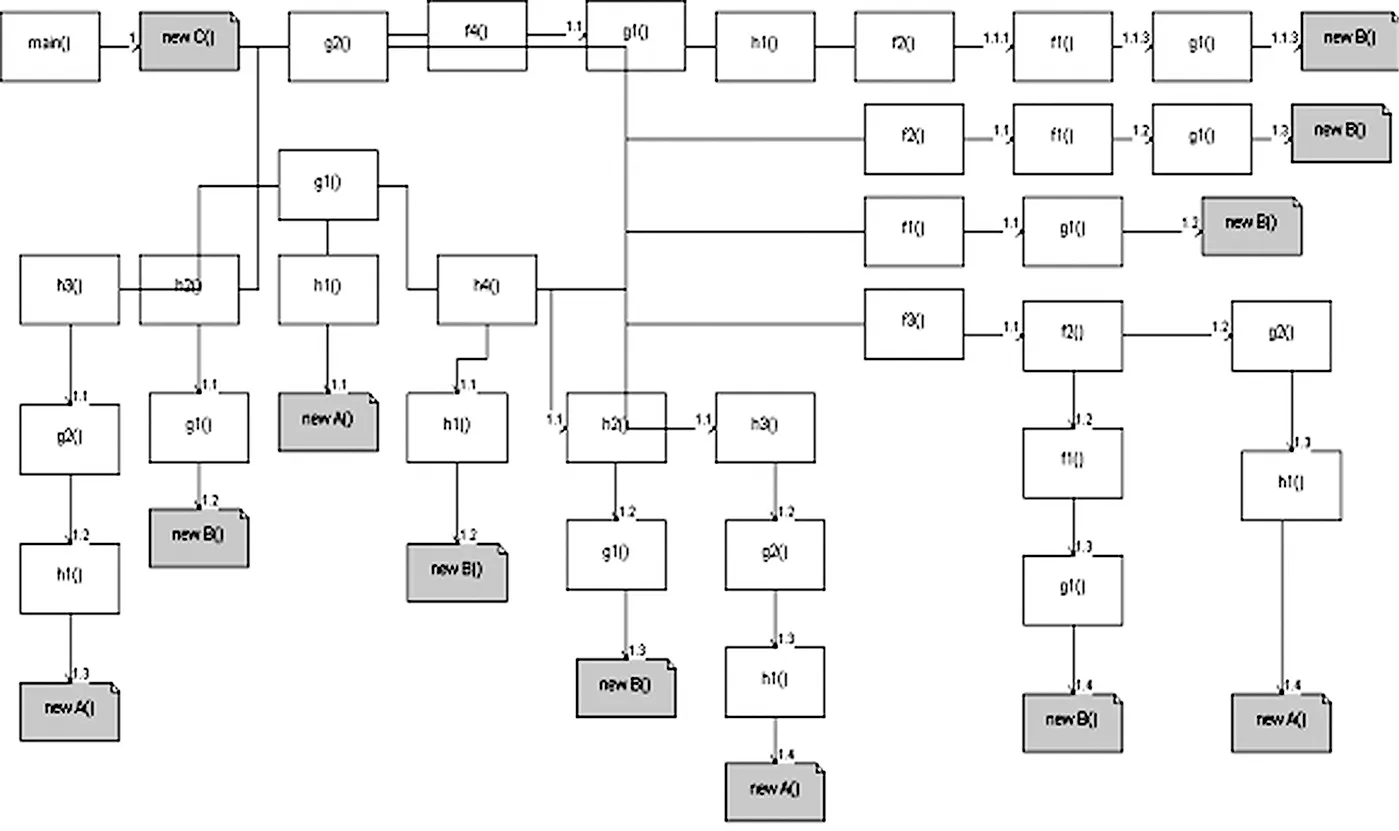
图1 产生的调用环境图

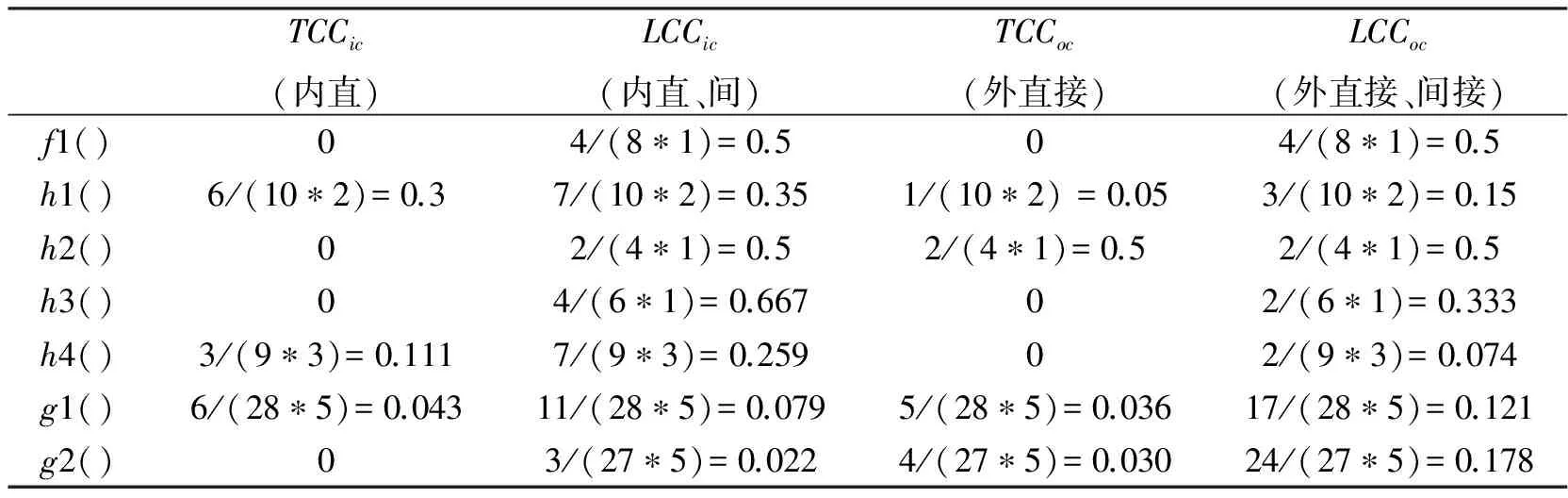
表1 方法的类间和类内度量值

[1]Eder J,Kappel G,Schrefl M.Coupleing and Cohesion in Object-Oriented Systems[R]. Technical Report,University of Klagenfurt,1994.

[2]Chidamber S R,Kemerer C F. Towards a Metrics Suit for Object Oriented design[C]. In Proc.Conference on Object Oriented Programming:System,Languages and Applications(OOPSLA'91), SIGPLAN Notices,1991, 26(11),197～211.

[3]Chidamber S R,Kemerer C F.A Metric Suit for Object-Oriented design[J]. IEEE Transactions on Software Engineering,1994, 20(6):476～493.

[4]Atanas Rountev， Scott Kagan， Michael Gibas．Static and Dynamic Analysis of Call Chains in Java[C]．ISSTA'04, July 11～14, 2004, Boston, Massachusetts, USA ACM．

[5]Lieberherr K J,Xiao C.Formal Foundation for Object-Oriented Data Modeling[J].in IEEE Transactions on knowledge and Data Engineering,1993,5:462～478.

Softwaremetricsbasedoncall-contexttree

WANG Feng-qin

(College of Physics and Electronic Science,Hubei Normal University,Huangshi 435002,China)

To extend the Call Context Tree, and to measure the coherency between the in classes and outer classes, based on the new measure formulas, this paper prove the properties which need to satisfy the feasibility of software measure.

call context tree; method measure; software measure

2013—12—10

湖北师范学院青年项目

王凤琴(1979— )，女，甘肃渭源人，硕士，讲师，研究方向为数字图像处理、软件度量、分布式程序设计、大数据算法分析.

TP311.5

A

1009-2714(2014)02- 0001- 04

10.3969/j.issn.1009-2714.2014.02.001