正整数方幂方阵的循序逐增规律与费马定理——兼证费马定理不成立的必要条件
张尔光
(韶关市人大机关,广东 韶关512000)
笔者研究结果表明,任何一个正整数方幂(n>1)均可表为数学方阵。正整数方幂方阵的各种数的循序逐增现象,反映了正整数方幂方阵的循序逐增规律性,而费马定理与此规律有着密切联系。
1 正整数2次幂方阵的循序逐增规律
笔者认为,要想弄清楚正整数方幂方阵的循序逐增规律性,应从对正整数2次幂方阵的研究入手,弄清楚正整数方幂方阵与正整数方幂的三角矩阵之间的关系,注重对正整数方幂方阵的各种数的循序逐增现象的研究,进而发现矩阵的各种数的循序逐增规律。
1.1 任何一个正整数平方均可表为由“1”组成的方阵或三角矩阵
笔者在《地图与数学的组合、排列及三角矩阵》一文(见《数学学习与研究》2011年第19期)中,经证明得出结论:任何一个正整数(n>1)的2次幂均可表为一个由“1”组成的方阵,而且这个方阵既可表为一个由“1”组成的三角矩阵,也可表为两个由“1”组成的三角矩阵。
根据正整数2次幂的方阵和三角矩阵的规律,遵循组合数“循序逐增”的基本原理,正整数的2次幂的方阵和三角矩阵可以图1来表示。其定理为
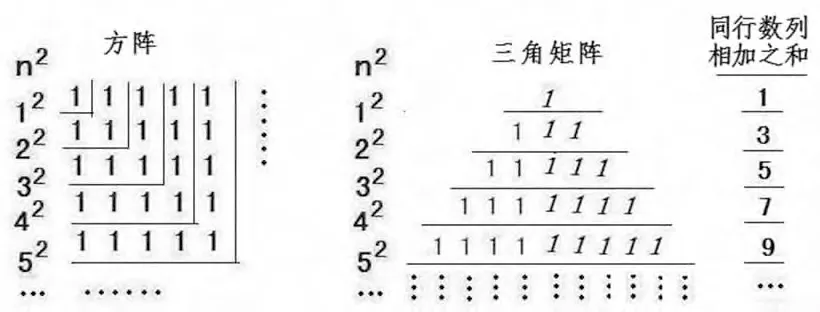
图1 n2的方阵和三角矩阵图
从“n2的方阵和三角矩阵图”看出,正整数2次幂的方阵,其方阵元素“1”是曲尺形排列,虽与三角矩阵的表达方式不同,但两者表达的意思(或叫内容)相同。可见,正整数方幂方阵与正整数方幂三角矩阵是等同关系。据此,为着论证的方便,笔者在下文论证正整数方幂方阵时,则以三角矩阵的表达方式来替代,并用之于证明方阵的各种数的循序逐增的规律。
1.2 方阵(三角矩阵)的各种数的概念
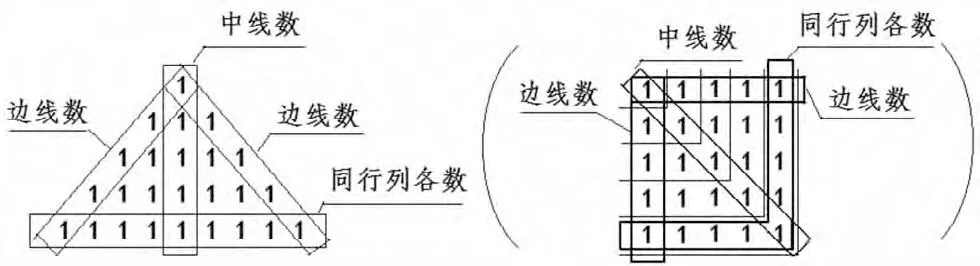
图2 三角矩阵(方阵)的各种数的概念解释图
本文所说的方阵(三角矩阵)的各种数,是指矩阵的边线数、中线数、同行数列相加之和(见图2图解)。所说的各种数的循序逐增现象,是指这些数及数列差反映出来的规律有序的东西。
从图2看出,边线数,是指三角矩阵的左斜边线数和右斜边线数,左斜边线数即是方阵的第一列数,右斜边线数即是方阵的第一行数;中线数,是指位于三角矩阵中间的数,即是方阵的左上角至右下角的斜线数;同行数列相加之和,是指三角矩阵同一行的数列各数相加后的得数,即是方阵的曲尺形行列数各数相加后的得数。
规律1 正整数2次幂方阵的同行数列相加之和是循序逐增的两个正整数平方差的依次排列。
从图1看出,正整数2次幂方阵(三角矩阵),其同行数列相加之和是循着奇数“1,3,5,7,9,…”的次序排列。这“1,3,5,7,9,…”,既是奇数,又是与正整数的2次幂有着密切联系的数:1是12-02之差,3是22-12之差,5是32-22之差,7是42-32之差,9是52-42之差,此后依次类推。可见,正整数2次幂方阵,其同行数列相加之和为循序逐增的两个正整数的平方差(即“n2-(n-1)2”之差)的依次排列,亦是循序逐增的两个正整数的同次方差(即“nk-(n-1)k”之差)的依次排列。这表明正整数方幂方阵是一个循序逐增的扩展过程。此规律是正整数方幂方阵的核心规律。
规律2 正整数2次幂方阵的同行数列相加之和的数列差是循序逐增的两组“两个正整数平方差”之差。
从“n2的方阵和三角矩阵图”的同行数列相加之和可知,正整数2次幂方阵的同行数列相加之和的数列差依次为“2,2,2,…”。此数列差“2”,是不同的前后两组“两个正整数平方差”之间的差。正整数方幂方阵的“同行数列相加之和的数列差”的公式为:
同行数列相加之和的数列差=[(n+1)k-nk]-[nk-(n-1)k]
如:1与3之差为2,已知1是“12-02”之差,3是“22-12”之差。据此,n为1,k为2,那么,得:[(1+1)2-12]-[12-(1-1)2]=(22-12)-(12-02)=3-1=2
再如:3与5之差为2,已知3是“22-12”之差,5是“32-22”之差。据此,n为2,k为2,那么,得:[(2+1)2-22]-[22-(2-1)2]=(32-22)-(22-12)=5-3=2
又如:5与7之差为2,已知5是“32-22”之差,7是“42-32”之差。据此,n为3,k为2,那么,得:[(3+1)2-32]-[32-(3-1)2]=(42-32)-(32-22)=7-5=2
2 正整数方幂方阵的各种数的循序逐增规律
笔者研究结果表明,遵循正整数方幂方阵的循序逐增规律,任何一个正整数方幂均可表为其同行数列相加之和为循序逐增的两个正整数的同次方差的方阵。
现以正整数的3次幂、4次幂、5次幂的方阵为例予以证明。例证1 正整数3次幂的方阵(三角矩阵),见图3。
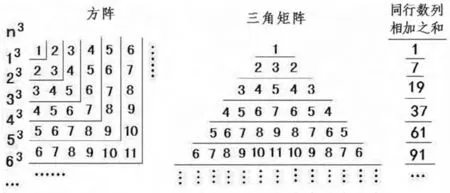
图3 正整数3次幂的方阵和三角矩阵
例证2 正整数4次幂的方阵(以三角矩阵表达),见图4。

图4 正整数4次幂方阵(以三角矩阵表达)
例证3 正整数的5次幂的方阵(以三角矩阵表达),见图5。
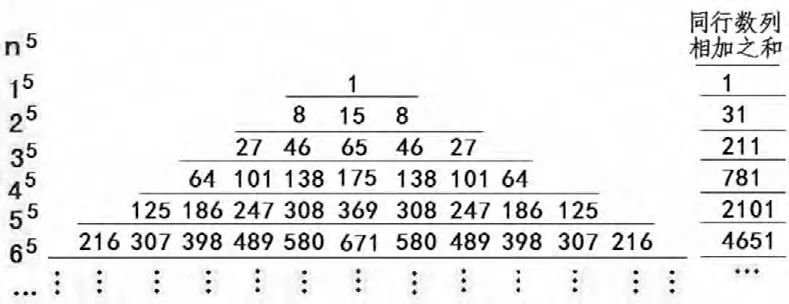
图5 正整数5次幂方阵(以三角矩阵表达)
2.1 正整数方幂方阵的同行数列相加之和及数列差的循序逐增规律
现依照正整数方幂方阵的循序逐增原理,对正整数的3次幂、4次幂、5次幂的方阵(三角矩阵)的各种数及数列进行分析。
从图3看出,正整数3次幂方阵,k=3,其同行数列相加之和依次为“1,7,19,37,61,…”,是前后两个正整数的同次方差(即“n3-(n-1)3”之差)的依次排列。“n3-(n-1)3”可表为“nk-(n-1)k”。
从图4看出,正整数4次幂方阵,k=4,其同行数列相加之和依次为“1,15,65,175,369,…”,是前后两个正整数的同次方差(即“n4-(n-1)4”之差)的依次排列。“n4-(n-1)4”可表为“nk-(n-1)k”。
从图5看出,正整数5次幂方阵,k=5,其同行数列相加之和依次为“1,31,211,781,2101,…”,是前后两个正整数的同次方差(即“n5-(n-1)5”之差)的依次排列。“n5-(n-1)5”可表为“nk-(n-1)k”。
依照归纳法,得出结论,正整数方幂方阵的同行数列相加之和为前后两个正整数的同次方差的依次排列。前后两个正整数的同次方差可表为“nk-(n-1)k”。
根据正整数方幂方阵的同行数列相加之和的循序逐增规律,可求得正整数方幂方阵的各行同行数列相加之和累加得数的循序逐增规律,也即是正整数方幂方阵的循序逐增规律。见图6。
根据图6反映出来的方阵的同行数列相加之和循序累加的规律,求得正整数方幂(方阵)的定理,即:

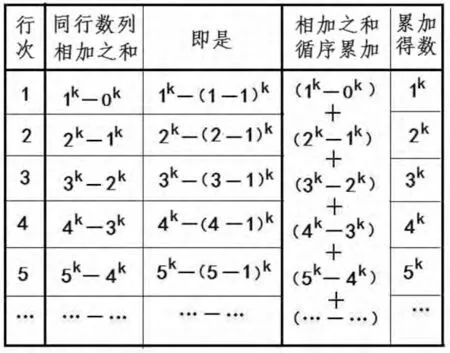
图6
根据方阵的同行数列相加之和循序累加的规律,可知:

根据正整数方幂方阵的同行数列相加之和数列,可求得正整数方幂方阵的同行数列相加之和数列差之定理为:
同行数列相加之和数列差=[(n+1)k-nk]-[nk-(n-1)k]
2.2 正整数方幂方阵的中线数及数列差的循序逐增规律
从图3看出,正整数3次幂方阵,k=3,其中线数数列依次为“1,3,5,7,9,…”,是前后两个正整数的“n3-1-(n-1)3-1”之差的依次排列。“n3-1-(n-1)3-1”可表为“nk-1-(n-1)k-1”。
从图4看出,正整数4次幂方阵,k=4,其中线数数列依次为“1,7,19,37,61,…”,是前后两个正整数的“n4-1-(n-1)4-1”之差的依次排列。“n4-1-(n-1)4-1”可表为“nk-1-(n-1)k-1”。
从图5看出,正整数5次幂方阵,k=5,其中线数数列为“1,15,65,175,369,…”前后两个正整数的“n5-1-(n-1)5-1”之差的依次排列.“n5-1-(n-1)5-1”可表为“nk-1-(n-1)k-1”。
依照归纳法,得出结论,正整数方幂方阵的中线数的循序逐增规律是前后两个正整数的“nk-1-(n-1)k-1”之差的依次排列。
根据正整数方幂方阵的中线数的循序逐增规律,可求得正整数方幂方阵的中线数数列差之定理为:[(n+1)k-1-nk-1]-[nk-1-(n-1)k-1]
2.3 正整数方幂方阵的边线数及数列差的循序逐增规律
从图3看出,正整数3次幂数方阵的边线数数列是“1,2,3,4,5,…”(即“13-2,23-2,33-2,43-2,53-2…”)的依次排列。 “13-2,23-2,33-2,43-2,53-2…”可表为“1k-2,2k-2,3k-2,4k-2,5k-2…”。
从图4看出,正整数4次幂数方阵的边线数数列是“12,22,32,42,52,…”(即“14-2,24-2,34-2,44-2,54-2…”)的依次排列。“14-2,24-2,34-2,44-2,54-2…”可表为“1k-2,2k-2,3k-2,4k-2,5k-2…”。
从图5看出,正整数5次幂数方阵的边线数数列是“13,23,33,43,53,…”(即“15-2,25-2,35-2,45-2,55-2…”)的依次排列。 “15-2,25-2,35-2,45-2,55-2…”可表为“1k-2,2k-2,3k-2,4k-2,5k-2…”。
依照归纳法,得出结论,正整数方幂方阵的边线数的循序逐增规律为“1k-2,2k-2,3k-2,4k-2,5k-2…”的依次排列。
已知正整数方幂方阵的边线数数列为“1k-2,2k-2,3k-2,4k-2,5k-2…”的依次排列,那么,可知边线数数列差的循序逐增规律,即:
第一行边线数与第二行边线数之差为“2k-2-1k-2”之差;
第二行边线数与第三行边线数之差为“3k-2-2k-2”之差;
第三行边线数与第四行边线数之差为“4k-2-3k-2”之差;
第四行边线数与第五行边线数之差为“5k-2-4k-2”之差;
第五行边线数与第六行边线数之差为“6k-2-5k-2”之差,此后依次类推。
2.4 正整数方幂方阵的同行边线数至中线数的数列差的循序逐增规律
根据正整数方幂方阵的中线数的循序逐增规律和边线数的循序逐增规律,可知:
第一行边线数与第二行边线数之差是为第二行边线数至中线数的数列差,即“2k-2-1k-2”之差;
第二行边线数与第三行边线数之差是为第三行边线数至中线数的数列差,即“3k-2-2k-2”;
第三行边线数与第四行边线数之差是为第四行边线数至中线数的数列差,即“4k-2-3k-2”;
第四行边线数与第五行边线数之差是为第五行边线数至中线数的数列差,即“5k-2-4k-2”。此后依次类推。2.5 正整数方幂方阵的规律模式
根据上文求得的正整数方幂方阵的各种数的循序逐增规律之定理,可构建组成正整数方幂方阵的规律模式,见图7、图8。
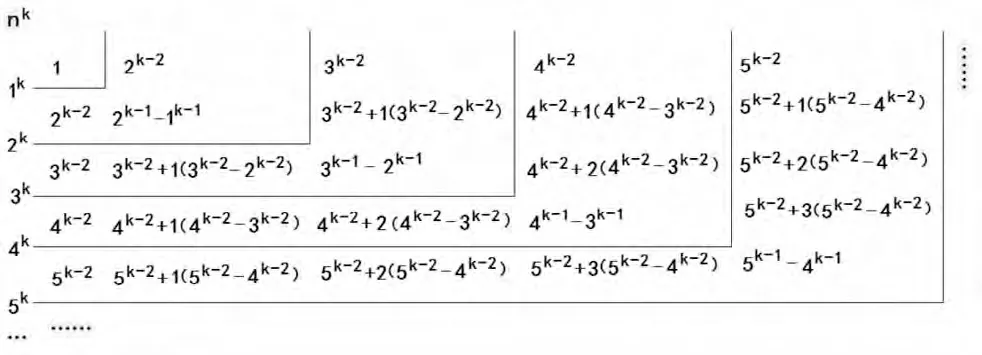
图7 (正整数方幂方阵的规律模式之一)

图8 (正整数方幂方阵的规律模式之二)
那么,依照正整数方幂方阵的规律模式可构建出正整数任何次幂(正整数n>1,次幂k>1)的方阵。对此,笔者无需举例赘证。
3 正整数的“xn+yn=zn”方程式与正整数方幂矩阵
正整数的“xn+yn=zn”方程式中的一种数学现象:
在正整数的“xn+yn=zn”方程式中,如将xn、yn、zn三者的次数由1至2、至3的等式做分析,不难发现其存在的一种数学现象。
事实告诉我们,当xn、yn、zn三者的次数为1(即n=1)时,即在“x+y=z(z≥2)”方程式中,任何一个z(即大于1的正整数)均可表为两个正整数相加之和,反之,任何两个正整数相加之和均可表为另一个正整数。因此,“x+y=z(z≥2)”成立。
事实还告诉我们,xn、yn、zn三者的次数为2时,即在“x2+y2=z2(z≥2)”方程式中,不可能做到任何一个大于1的正整数平方(即z2)均可表为两个正整数平方相加之和,比如62、72、82不可能表为一个正整数平方加另一个正整数平方;反之,也不可能做到任何一个正整数平方加一个正整数平方等于另一个正整数平方(即z2),比如“22+32”、“32+52”、“45+52”,其和不可能等于另一个正整数平方。因此,在“x2+y2=z2(z≥2)”方程式中,只是存在部分一个正整数平方(即z2)可表为两个正整数平方相加之和,部分一个正整数平方加一个正整数平方等于另一个正整数平方(即z2)。所以,正整数的“x2+y2=z2(z≥2)”方程式有成立与不成立之分。
事实和费马定理告诉我们,xn、yn、zn三者的次数为3时,即在“x3+y3=z3(z≥2)”方程式中,任何一个正整数三次方(即z3)均不可能表为两个正整数三次方相加之和,反之,任何两个正整数三次方相加不可能等于另一个正整数三次方(即z3)。因此,正整数的“x3+y3=z3(z≥2)”不成立
可见,在正整数的“xn+yn=zn”方程式中,幂的次数仅是从1至2、至3的增升,其结果就发生了“完全成立→部分成立→完全不成立”如此截然不同的质的变化。正整数的“xn+yn=zn”方程式中反映出来的幂的次数循序逐增现象,有它的不可理解性。显然,如从正整数的“x2+y2=z2”的成立等式和不成立等式的异同之处入手,运用方阵等式的方法来研究它,这对于另辟蹊径破解费马定理是有积极意义的。
4 正整数的“x2+y2=z2”中成立等式与不成立等式的异同
笔者研究结果表明,在成立的正整数的“x2+y2=z2”的方阵等式中又分为两类,一类是z2方阵的“末行数列相加之和”等于x2的方阵等式;另一类是x2、y2、z23个方阵是为方阵群的方阵等式,其3个方阵群是前一类方阵等式的3个方阵分别乘上“n2”而组成。
4.1 z2方阵的“末行数列相加之和”等于x2的方阵等式的证明
根据正整数的“x2+y2=z2”的方程式可知,z2方阵>x2方阵、y2方阵。笔者依照从小到大的次序,设定x2方阵<y2方阵<z2方阵。那么,在z2方阵的“末行数列相加之和”等于x2的方阵等式中,x2、y2、z23个方阵之间存在什么内在联系呢?为此,请看图9。
为着证明的表述不发生混淆,方阵的“同行数列相加之和”的行次以“z”表示。
从图9看出,当方阵的z行的“同行数列相加之和”为奇数平方时,必定会产生一个成立的“x2+y2=z2”的方阵等式。
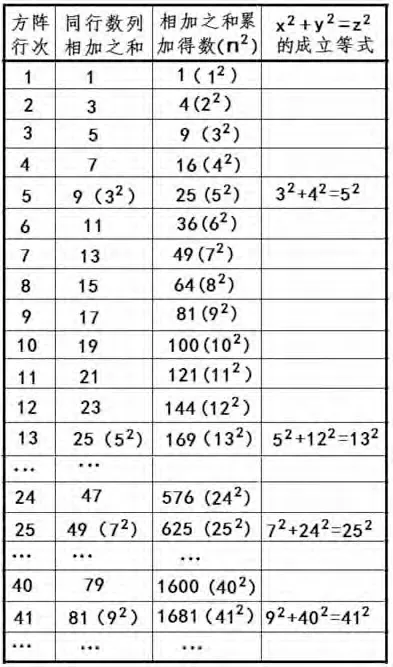
图9
如,方阵第5行“同行数列相加之和”9为32,就产生了“32+42=52”的成立等式,即z2为52,y2为42,x2为32;
再如,方阵第13行“同行数列相加之和”25为52,就产生了“52+122=132”的成立等式,即z2为132,y2为122,x2为52;
又如,方阵第25行“同行数列相加之和”49为72,就产生了“72+242=252”的成立等式,即z2为252,y2为242,x2为72。
从图9中成立的“x2+y2=z2”的方阵等式看出,y2方阵就是z2方阵减去末行数列而形成的方阵,x2方阵的x2等于z2方阵的“末行数列相加之和”。据此,可以说,y2方阵和x2方阵是z2方阵分解出来的两个完整的方阵。为此,现对z2方阵做分解证明。
为便于区别,将z2方阵的末行元素以“①”来表示。
例证1 “52=42+32”方阵等式的z2方阵的分解证明
已知 z2方阵为52方阵,z2=52。
第一步 将52方阵的末行数列分解出去,则为y2方阵,即方阵等式中的42方阵。可见,(5-1)2=42,表为(z-1)2=y2。
第二步 将52方阵分解出来的末行数列组成x2方阵,即方阵等式中的32方阵。可见,52-(5-1)2=32,表为z2-(z-1)2=x2。z2方阵的“末行数列相加之和”等于x2。
第三步 将z2方阵及分解形成的y2方阵和x2方阵表为方阵等式:

从上方阵等式看出,52方阵=42方阵+32方阵。可见,“52=42+32”的方阵等式成立。此证。
例证2 “132=122+52”方阵等式的z2方阵的分解证明
已知 z2方阵为132方阵,z2=132。
第一步 将132方阵的末行数列分解出去,则为y2方阵,即方阵等式中的122方阵。可见,(13-1)2=122,表为(z-1)2=y2。
第二步 将132方阵分解出来的末行数列组成x2方阵,即方阵等式中的52方阵。可见,132-(13-1)2=52,表为z2-(z-1)2=x2。z2方阵的“末行数列相加之和”等于x2。
第三步 将z2方阵及分解形成的y2方阵和x2方阵表为方阵等式:

从上方阵等式看出,132方阵=122方阵+52方阵。可见,“132=122+52”的方阵等式成立。此证。
例证3 “252=242+72”方阵等式的z2方阵的分解证明
已知 z2方阵为252方阵(方阵元素以点表示1),z2=252。
第一步 将252方阵的末行数列分解出去,则为y2方阵,即方阵等式中的242方阵。可见,(25-1)2=242,表为y2=(z-1)2。
第二步 将z2方阵分解出来的末行数列组成x2方阵,即方阵等式中的72方阵,可见,252-(25-1)2=72,表为z2-(z-1)2=x2。z2方阵的“末行数列相加之和”等于x2。
第三步 将z2方阵及分解形成的y2方阵和x2方阵表为方阵等式:

从上方阵等式看出,252方阵=242方阵+72方阵。可见,“252=242+72”的方阵等式成立。此证。
综上例证1、例证2、例证3的证明,依照归纳法,可知z2方阵的“末行数列相加之和”等于x2的方阵等式中的x2、y2、z23个方阵之间的关系:
结论1 y2方阵是z2方阵减去末行数列后形成的方阵,可表为(z-1)2=y2。
结论2 x2方阵是由z2方阵的末行数列组成的方阵,z2方阵的“末行数列相加之和”等于x2,可表为z2-(z-1)2=x2。
结论3 z2方阵可分解为2个小于其的完整的方阵,即为y2方阵和x2方阵,可表为z2=y2+x2=(z-1)2+[z2-(z-1)2]。4.2 x2、y2、z23个方阵是为方阵群的方阵等式
例证1 “62+82=102”的方阵等式
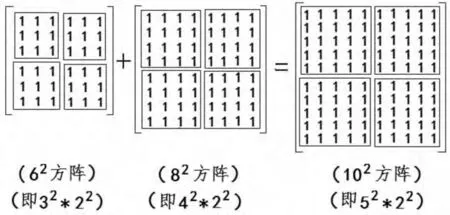
从“62+82=102”的方阵等式可知,x2方阵为62方阵,而62=(32*22),表明62方阵是由“22”个32方阵组成的方阵群;y2方阵为82方阵,而82=(42*22),表明y2方阵是由“22”个42方阵组成的方阵群;z2方阵102方阵,而102=(52*22),表明z2方阵是由“22”个52方阵组成的方阵群。由此可知,“62+82=102”的方阵等式的3个方阵,是“32+42=52”的方阵等式的3个方阵分别乘上“22”而组成的方阵群,即“62+82=102”等于“(32*22)+(42*22)=(52*22)”。又从102方阵可知,其末两行的“同行数列相加之和”相加(即17+19)之和为36,而36=62,正是“102-82”(即“z2-y2”)之差。可见,z2-y2=x2。“62+82=102”的方阵等式成立。
例证2 “92+122=152”的方阵等式
从“92+122=152”的方阵等式可知,x2方阵为92方阵,而92=(32*32),表明92方阵是由“32”个32方阵组成的方阵群;y2方阵为122方阵。而122=(42*32),表明y2方阵是由“32”个42方阵组成的方阵群;z2方阵为152方阵,而152=(52*32),表明z2方阵是由“32”个52方阵组成的方阵群。由此可知,“92+122=152”的方阵等式的3个方阵,是“32+42=52”的方阵等式的3个方阵分别乘上“32”而组成的方阵群,即“92+122=152”等于“(32*32)+(42*32)=(52*32)”。又从152方阵可知,其末三行的“同行数列相加之和”相加(即25+27+29)之和为“81”,而“81”=92,正是“152-122”(即“z2-y2”)之差,可见,z2-y2=x2。“92+122=152”的方阵等式成立。
综上例证1、例证2的证明,x2、y2、z23个方阵为方阵群的方阵等式的特征可归纳为:
特征1 z2、y2、x2此3个方阵群是z2方阵的“末行数列相加之和”等于x2的方阵等式的3个方阵分别乘上“n2”而组成。
特征2 z2方阵减去y2方阵(即“z2-y2”)之差,是正整数平方,等于x2方阵的x2,可表为x2=z2-y2。
4.3 两类正整数的“x2+y2=z2”中成立等式的关系及共同特征
从上证明可知,z2方阵的“末行数列相加之和”等同于x2的方阵等式,与x2、y2、z23个方阵为方阵群的方阵等式具有源与流的关系。后者的z2、y2、x23个方阵为前者的z2、y2、x23个方阵分别乘上“n2”而组成的方阵群。据此,在已知前者的3个方阵的条件下,同时乘上“n2”,可知后者的z2、y2、x23个方阵群,求得后者的“x2+y2=z2”的成立等式。见图10。
从图10看出,z2方阵的“末行数列相加之和”等于x2的方阵等式存在,那么,x2、y2、z2为方阵群的方阵等式必定存在。可见,前者衍生后者,后者延伸前者,两者是源与流的关系,是一脉相承的同一本质的方阵等式。正因为如此,所以,在两者的“x2+y2=z2”的方阵等式中,不论是x2=z2-y2,还是y2=z2-x2都是成立的。而这,正是两类正整数的“x2+y2=z2”的成立等式的共同特征。
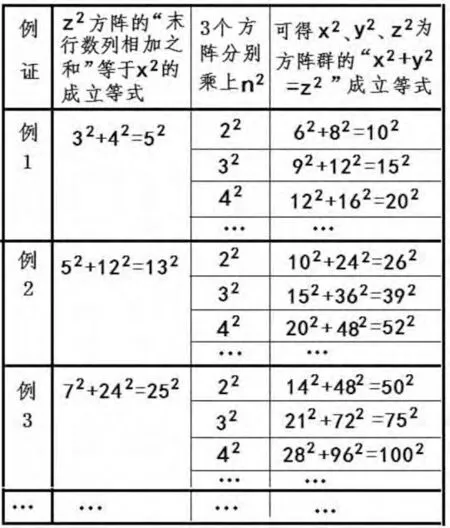
图10
遵循正整数方幂方阵的循序逐增规律,根据“x2+y2=z2”方阵等式中x2、y2、z23个方阵之间的关系,可设定,z2方阵是存在的已知方阵,y2方阵也是存在的已知方阵(即为“(z-1)2方阵”),而未知的则是x2方阵,即z2方阵的“末行数列相加之和”(即“z2-(z-1)2”之差)是否等于x2。基于这一解读,在求证正整数的“x2+y2=z2”的等式时,只需求证z2方阵的“末行数列相加之和”是否等于x2这个关键点便见分晓,而无需作更多的证明。
4.4 正整数的“x2+y2=z2”不成立等式的根本原因
例证1 62=52+x2等式的z2方阵的分解证明
已知 z2方阵为62方阵(见图11),62方阵减去末行数列而形成的y2方阵为52方阵(即(6-1)2=52);需求证的是62方阵的“末行数列相加之和”(即“62-(6-1)2”)是否等于x2。

图11
从62方阵可知,其“末行数列相加之和”为62-(6-1)2=11≈3.1662,不是正整数平方。而由62方阵的末行数列(元素)组成的x2方阵(见图12),处于32余2、42缺5之状态,是不完整的正整数2次幂方阵。可见,62方阵分解的两个方阵,y2方阵为52方阵成立,而x2方阵是不完整的方阵。所以,62=52+x2等式作为正整数的“x2+y2=z2”等式是不成立的等式。此证。
图12
例证2 72=62+x2等式的z2方阵的分解证明
已知 z2方阵为72方阵(见图13),72方阵减去末行数列而形成的y2方阵为62方阵(即“(7-1)2=62”),需求证的是72方阵的“末行数列相加之和”(即“72-(7-1)2”之差)是否等于x2。
图13
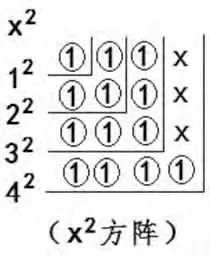
图14
从72方阵可知,其“末行数列相加之和”为72-(7-1)2=13≈3.60562,不是正整数平方。而由62方阵的末行数列(元素)组成的x2方阵(见图14),处于32余4、42缺3之状态,是不完整的正整数2次幂方阵。可见,72方阵分解的两个方阵,y2方阵为62方阵成立,而x2方阵是不完整的方阵。所以,72=62+x2等式作为正整数的“x2+y2=z2”等式是不成立的等式。此证。
综合例证1、例证2的证明,得出结论:正整数的“x2+y2=z2”不成立等式的根本原因,在于z2方阵的“末行数列相加之和”(即“z2-(z-1)2”之差)不可表为正整数的平方,z2方阵只能分解为一个完整的y2方阵和一个不完整的x2方阵。
4.5 正整数的“x2+y2=z2”的成立等式与不成立等式的区别
从以上的方阵等式证明可知,正整数的“x2+y2=z2”的成立等式与不成立等式的区别主要在于z2方阵的“末行数列相加之和”(即“z2-(z-1)2”之差)是否等于x2,成立的等式,z2-(z-1)2=x2(包括x2、y2、z2分别乘上“n2”后的“x2=z2-y2”),x2的x是正整数;不成立的等式,则z2-(z-1)2≠x2(包括x2、y2、z2分别乘上“n2”后的“x2≠z2-y2”),x2的x不是正整数。这种区别,还反映在方阵的“同行数列相加之和”与“相加之和累加得数”的两种数字之关系的不同。成立的等式,因z2方阵的“同行数列相加之和”的平方根是正整数,所以,在“相加之和累加得数”中存在其等同数;不成立的等式,因z2方阵的“同行数列相加之和”的平方根不是正整数,所以,在“相加之和累加得数”中不存在其等同数。
4.6 结论
综上正整数的“x2+y2=z2”的方阵等式的证明,得出结论:
结论1 在正整数的“x2+y2=z2”的方阵等式中,z2方阵是方阵等式的核心方阵,是设定的已知方阵。可通过已知的z2方阵,推知y2方阵的y2=(z-1)2,x2方阵的x2=z2-(z-1)2。
结论2 z2方阵的“末行数列相加之和”(即z2-(z-1)2)是组成x2方阵的元素,是方阵等式的关键要素。
结论3 “x2=z2-(z-1)2”的x为正整数是方阵等式成立的必要条件,是求证方阵等式是否成立的关键点。
5 对费马定理的证明
1995年英国数学家安德鲁·怀尔斯与其学生理查·泰勒应用椭圆曲线的原理对费马定理做出了证明。笔者认为,费马定理是一个关于正整数方幂之间关系的方程式命题,应用正整数方幂方阵的原理对其做出证明,这似乎更合乎该命题的题意。基于这个观点,笔者尝试运用方阵等式的证明方法,从费马定理不成立的必要条件的角度,对费马定理进行论证。
5.1 费马定理的另一种表述
四川科学技术出版社于1985年出版的《古今数学趣话》一书的《能下金蛋的母鸡——“费马猜测”古今谈》对费马定理的原本内容是这样表述的:“不可能把一个整数的立方表为两个整数的立方和,也不可能把一个整数的四次幂表为两个整数的四次幂和。一般来说,不可能把任意一个次数大于2的整数的方幂,表为两个整数的同次方幂之和。”用现代的专业用语来说,就是当n>2时,不定方程:
xn+yn=zn不存在正整数解。
笔者认为,上段文字关于费马定理的内容,用正整数方幂方阵的原理的语言来表述,则为:
不可能把一个整数的立方的方阵表为两个整数的立方的方阵,也不可能把一个整数的四次幂的方阵表为两个整数的四次幂的方阵。一般来说,不可能把任意一个次数大于2的整数的方幂的方阵,表为两个整数的同次方幂之方阵。其不定方阵等式为
xn方阵+yn方阵=zn方阵 n>2时不存在正整数解。

图15
5.2 对“xn+yn≠zn”(n≥3)的证明
根据对正整数的“x2+y2=z2”的方阵等式的证明结论,遵循正整数方幂方阵的循序逐增原理,在正整数次幂n>2的“xn+yn=zn”的方阵等式中,同样zn方阵是设定的已知方阵,yn方阵为zn方阵减去末行数列而形成的方阵﹝即yn=(z-1)n﹞,是可推知的方阵,而xn方阵的“xn=zn-(z-1)n”x为正整数是方阵等式成立的必要条件,zn方阵的“末行数列相加之和”是否等于xn,是求证方阵等式是否成立的关键点。对此,既可从方阵的“同行数列相加之和”的数字中有无与“相加之和累加得数”等同的数予以验证,也可直接对“xn=zn-(z-1)n”做出证明。
5.2.1 方阵的“同行数列相加之和”中无与“相加之和累加得数”等同的数
事实证明,在正整数次幂n>2后,方阵的“同行数列相加之和”中(“1”除外,下同)不存在有与“相加之和累加得数”等同的数。请看图15。
图15是正整数1至11、次幂为3至7的方阵的“同行数列相加之和”和“相加之和累加得数”的统计表。从该表看出,在正整数的3次幂、4次幂、5次幂、6次幂、7次幂的方阵的两种数字中,2至11行的“同行数列相加之和”中均不存在有与“累加得数”等同的数。据此,得出结论:在正整数次幂n>2后,方阵的“同行数列相加之和”的数字中(1除外)不存在有与“相加之和累加得数”等同的数。
5.2.2 对“xn=zn-(z-1)n”的“x”是不是正整数的证明
笔者研究结果表明,在正整数次幂n>2后,之所以方阵的“同行数列相加之和”中不存在有与“相加之和累加得数”等同的数,这是因为,“xn=zn-(z-1)n”等式中的“x”不是正整数。
例证1 以正整数的3次幂方阵的“同行数列相加之和”为例

综上实例证明,得出结论,在“x3=z3-(z-1)3”等式中,在z为正整数的条件下,“x”不是正整数,即“z3=y3+x3”不存在正整数解。此证。
例证2 以正整数4次幂方阵的“同行数列相加之和”为例


综上实例证明,得出结论,在“x4=z4-(z-1)4”等式中,在z为正整数的条件下,“x”不是正整数,即“z4=y4+x4”不存在正整数解。此证。
例证3 以正整数5次幂方阵的“同行数列相加之和”为例


综上实例证明,得出结论,在“x5=z5-(z-1)5”等式中,在z为正整数的条件下,“x”不是正整数,即“z5=y5+x5”不存在正整数解,此证。
依照归纳法,得出结论:在“xn=zn-(z-1)n”等式中,在z为正整数的条件下,“x”不是正整数。因此,“zn=yn+xn”不存在正整数解。所以,费马定理成立。此证。
5.2.3 对“xn=zn-(z-1)n”等式是否成立的证明
在z、x均为正整数的条件下,“xn=zn-(z-1)n”等式是否成立呢?现予以证明。
设定“z2=y2+x2”是成立的正整数2次幂的方阵等式。据此,次幂n>2时,依照正整数方幂方阵的原理,“zn=yn+xn”可表为:
z2*zn-2=(y2*yn-2)+(x2*xn-2)
正整数方幂方阵的循序逐增原理告诉我们,在正整数次幂n>2时,不论正整数z及方幂如何升增,“z2*zn-2=zn”都是成立的。而作为zn方阵减去末行数列而形成的yn方阵,不论zn方阵的z及n如何升增,其“yn=(z-1)2*(z-1)n-2”(即“(z-1)n=(z-1)2*(z-1)n-2)”)都是成立的。(如,设zn=53,已知z=5,n=3,那么,yn=(z-1)2*(z-1)n-2=(5-1)2*(5-1)3-2=42*4=43;又如,设zn=67,已 知z=6,n=7,那 么,yn=(z-1)2*(z-1)n-2=(6-1)2*(6-1)7-2=52*55=57。)
那么,当zn方阵的n>2时,其“zn-(z-1)n=xn”是否成立呢。对此,将该等式分为“zn-(z-1)n”(zn方阵的“末行数列相加之和”)和“xn”(即xn方阵的xn)两部分来解读,q并做出证明。
依照zn方阵的zn=z2*zn-2的表达方式,zn方阵的末行数列相加之和“zn-(z-1)n”则可表为:(z2*zn-2)-[(z-1)2*(z-1)n-2]

例证1 设z2=y2+x2为52=42+32,现求证zn方阵为53方阵时,“zn-(z-1)n=xn”是否成立。
已知 z=5,n=3。那么,将“z=5,n=3”套入“(z2*zn-2)-[(z-1)2*(z-1)n-2]”得:

可见,53-43≠33,zn-(z-1)n≠xn。所以,“zn-(z-1)n=xn”不成立。此证。
例证2 设z2=y2+x2为132=122+52,现求证zn方阵为135方阵时,“zn-(z-1)n=xn”是否成立。
已知z=13,n=5。那么,将“z=13,n=5”套入“(z2*zn-2)-[(z-1)2*(z-1)n-2]”得:(132*135-2)-[(13-1)2*(13-1)5-2]=135-125=371293-248832=122461可见,135-125≠55,zn-(z-1)n≠xn。所以,“zn-(z-1)n=xn”不成立。此证。例证3 设z2=y2+x2为252=242+72,现求证zn方阵为254方阵时,“zn-(z-1)n=xn”是否成立。
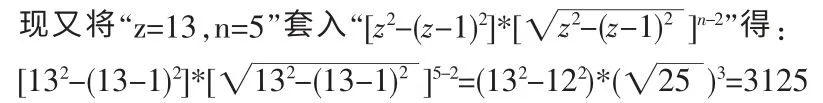
已知z=25,n=4。那么,将“z=25,n=4”套入“(z2*zn-2)-[(z-1)2*(z-1)n-2]”得:
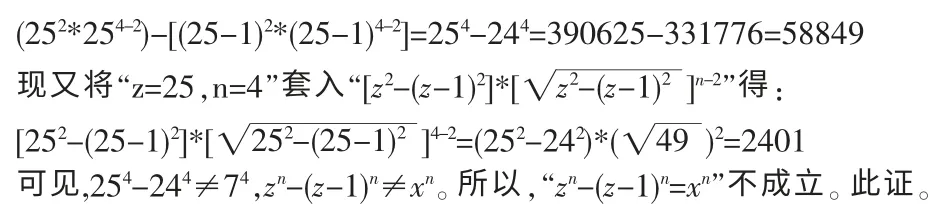
综例证1、例证2、例证3的证明,依照归纳法,得出结论:当正整数次幂n>2时,因为zn-(z-1)n≠xn,所以,“zn-(z-1)n=xn”不成立。当正整数次幂n>2时,因为“zn-(z-1)n=xn”不成立,所以,“zn=yn+xn”也不成立。此证。
5.3 总的证明结论
事实上,根据“xn方阵+yn方阵=zn方阵”成立等式的必要条件和费马定理给出的“同次方幂”的原则,用逆向思维方式去思考,不难明白,对费马定理的证明,其实就是对“(x2*xn-2)+(y2*yn-2)≠z2*zn-2”做出证明。现证明如下:

同 理,∵zn-2>yn-2,∴(y2*yn-2)÷zn-2<y2,亦 即(y2*yn-2)<(y2*zn-2),或 是(y2*yn-2)≠(y2*zn-2)。
由此得出结论:(x2*xn-2)+(y2*yn-2)≠z2*zn-2。所以,费马定理成立。此证。
[1]张尔光.正整数的方幂的方阵与费马定理——费马定理不成立的必要条件[J].数学学习与研究,2012,23:115-119.

