基于PBL的离散数学课程教学创新实践

李 俊 诸葛霞 廖远江

（宁波工程学院电子与信息工程学院，浙江 宁波315016）

0 引言

“离散数学”课程是研究离散量的结构和相互间关系的一门学科，它充分描述了计算机科学离散性的特点，是计算机科学技术及相关专业的核心课程，可以为计算机科学技术及相关专业的学生提供重要的理论基础，例如程序设计语言、数据结构、数据库技术、算法分析、可计算性与计算复杂性理论、逻辑设计、系统结构、容错诊断、人工智能与机器定理证明等课程[1-2]。

为了能激发学生学习的积极性，达到最佳的教学目的,本文通过调研和结合近年来的教学实际情况，从教学方法和手段等方面进行探索,提出了基于PBL教学模式的“离散数学”课程教学创新实践。

1 “离散数学”教学现状分析

“离散数学”是计算机科学技术及相关专业的骨干课程[3]，与其他计算机课程相比有相似的方面，但也有其独特的地方，分析“离散数学”课程的特点，以及在教学实践中常存在的问题主要体现在以下几个方面：

（1）离散数学定义多、定理多，内容抽象，逻辑性强,大多数教师只重视理论知识的教授，忽略了实践环节，使学生误认为离散数学是一门理论课，对本专业的实际应用作用不大,因此不重视学习，甚至出现厌学心理。

（2）离散数学课程中的定义和定理难理解难记忆，公式和证明也特别多，有些学生掌握了基础知识，也背会了定义、定理和公式，但不会做题，所以很多学生认为离散数学是一门难学的课程，甚至有些学生认为离散数学是计算机专业中最难学的课程。

（3）离散数学内容丰富，包含数理逻辑、集合论、代数系统、图论、组合数学等多个知识点。大多数教师能认真深入地讲好每个知识点,但是很少老师会把这些知识点之间的联系介绍出来，所以使大部分学生误认为离散数学课程是由几个相互独立的知识点组成，各知识点之间联系少，缺少体系完整性，导致学生对课程内容理解的不深入和透彻，达不到学习目的。

（4）离散数学内容多，课时少，一般高校在教学培养计划中将该课程设置为64学时，甚至有的学校设置成54学时[4]，在这些学时中教师只能主要以追求讲授理论知识为主，缺少理论联系实际的实践教学环节，导致学生不知道到如何使用这门学科为计算机科学的应用和发展提供有效地服务。

针对“离散数学”课程的特点，以及在教学实践中存在的这些问题，本文提出一种基于PBL的教学模式用于“离散数学”课程的教学研究，通过以问题为导向，倡导以学生主动学习为主的教育方式使学生认识到学习离散数学对计算机专业的重要性，以及激发学生学习的积极和主动性。

2 基于PBL离散数学教学方法

离散数学是计算机专业的一门核心课程，为了提高教学质量，达到教学目的，以及理论知识与实践技能协同发展和互相促进，本文提出了一种基于PBL教学模式的“离散数学”教学研究。其教学模式是：

（1）上课前，为了使学生对教学新内容产生浓厚的兴趣和强烈的求知欲，提高学习效率和课堂的教学质量，教师针对学生的专业知识特点及授课任务，设计可行有效的教学方案，并结合授课内容提出和专业知识相关的一道或若干道问题,以问题为导向要求学生围绕所提问题充分预习教材、查找相关资料、课下分组探讨解决方案。例如在讲图论中的最短路径知识时可以向学生提出下面的从一个城市到另一个城市的最短路径问题，使学生围绕该问题预习和探讨授课新内容。

所提问题：图1为7个城市A，B，C，D，E，F，G之间的一个公路图，该图用G表示，结点（用V表示）代表城市，边（用E表示）代表城市之间的公路，边上的权值（用W表示）表示该段公路的长度。考虑编写一个程序的算法，该算法能够自动算出从一个城市到另一个城市的最短路径及距离。

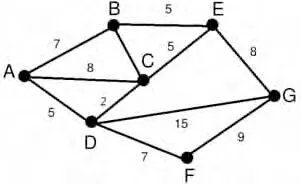
图1 城市公路图

（2）课堂内，教师首先鼓励学生积极发言，让学生以解决问题为支架陈述其自学方法、自学过程、自学内容，以及解决问题的方；然后教师讲授教学内容，讲解应用教学新内容对所提出问题的解决方案；最后教师对学生所提出问题的解决方案给予评价，对其有解决方法较好和具有创新想法的同学给予赞赏，对解决方法不足之处给予补充，以有效地培养和训练学生自主学习，分析问题，解决问题和创造思维能力。例如上面求最短路径问题，我们首先讲解最短路径知识，然后利用该知识给出下面的从一个城市到另一个城市的最短路径及距离的解决方案，再对学生所提出问题的解决方案给予评价。

从一个城市到另一个城市的最短路径及距离的解决方案：给出一个城市到其余城市的最短路径及距离算法，其它城市之间的最短路径及距离可以类似解出[5]。下面以图1中的A城市为例，介绍一个城市到其余城市的最短路径及距离算法求解的主要步骤：

（1)把图1中城市集合V分成两组：第一组为已求出最短路径的城市集合(用S表示)，第二组为其余未确定最短路径的城市集合(用U表示)。初始时,S只包含城市A，即S={A}，A到A的距离为0。U包含除A外的其他城市，即U={B,C,D,E,F,G}，U中各城市到城市A的距离为边上的权值(若两城市之间有公路)或∞(若两顶点之间无公路)。

（2)把k加入S中(该选定的距离就是城市A到城市k的最短路径长度)。

（3)以k为新考虑的中间点,修改U中各城市的距离：若从城市A到城市u(u∈U)的距离(经过城市k)比原来距离(不经过城市k)短,则修改城市u的距离值,修改后的距离值的城市k的距离加上边fflt;k,u＞上的权。

（4)重复步骤（b)和(c)直到所有城市都包含在S中。

(3)课堂后，让学生上机实验，把问题程序化，以帮助学生加深对所学知识的理解与消化，同时也锻炼学生编程能力和应用离散数学的理论知识解决计算机专业实际问题的能力。

3 结束语

针对“离散数学”课程特点，本文通过调研和结合近年来的教学实际情况，从教学方法和手段等方面进行探索，提出了一种基于PBL教学模式的“离散数学”课程教学创新实践，即教师课前提出问题——学生查找资料、分组讨论——教师教授新内容和给出问题的解决方案——学生上机实践。该模式即能给学生提供有针对性的思维支架，激发学生学习的积极性，又有助于教师从多方面考虑PBL理念的方法在教学中的应用，提升教学设计的有效性，达到教与学的目标。

［1］屈婉玲.离散数学[M].高等教育出版社,2008.

［2］文海英,廖瑞华,魏大宽.离散数学课程教学改革探索与实践[J].计算机教育,2010,(6)：100-103.

［3］张蕾,黄文芝.“离散结构”课程的教学探索[J].中国电力教育,2011(17)：96-101.

［4］谭作文.离散数学课程中实验教学探讨[J].计算机教育,2010(6)：106-109.

［5］李春葆,尹为民,等.数据结构教程[M].清华大学出版社,2009.