基于禽流感的一类模型建立与稳定性分析

车淑琴 薛亚奎

（中北大学理学院，山西 太原030051）

0 引言

禽流感（Avian Influenza），全名鸟禽类流行性感冒，它是一类复杂的病毒，不仅能感染家禽（鸡鸭），也能感染一些哺乳类动物（猪、狗、马），随着禽流感病毒的不断突变，它甚至可以感染人类，并造成较高的死亡率，禽流感突变和蔓延及其严重使得人类对它的研究预防和控制变的非常困难。数学建模可以直观有效的帮助我们研究禽流感的发展规律，最早人们研究的是鸟类迁徙的禽流感传播模型[1]，后来人们主要研究的对象是人类，预防控制也集中在人类如文献[2-5]，这样确实可以有效的减少禽流感对人类的伤害；也有一些文章开始着重于解决禽流感对家禽的感染情况，如文献[6]分析了H5N1在种群内的传播。

本文中把禽类分为三个仓室：易感者(X)，染病者(Y)，接种免疫者(V)，人类分为易感者(S)，染病者(I)，隔离治疗者(T)。μA为禽类的出生率，μ和d分别为禽类和人类的自然死亡率，α和δ分别为染病的禽类和人类的因病死亡率，q2(0fflt;q2fflt;1)是新生禽类具有免疫力的比例，q1=1-q2是新生禽类不具有免疫力的比例，p为禽类预防接种比例；ε是免疫失效比例，β和σβ(0fflt;σfflt;1)分别为染病的禽类感染易感禽类和具有免疫力禽类的感染率，Λ为人口的出生率，ω为染病的禽类感染易感人类的传染率，θ是隔离者的康复率，γ是患者的隔离率，这些参数均为正参数。模型如下：

文章组织如下：在第二部分中，证明了无病平衡点和正平衡点的存在性；在第三部分中，证明了该系统无病平衡点和正平衡点的全局稳定性；最后，分析结果。

1 平衡点的存在性

系统的正平衡点E+(X*,V*,Y*,S*,I*,T*)可以由方程组（2）计算得出

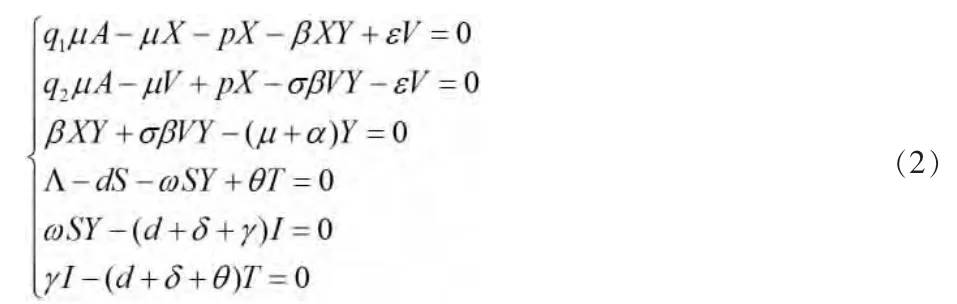
由方程组（2）可以得到：

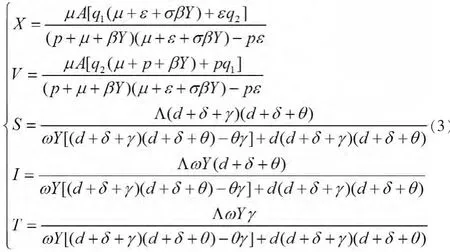
并且有

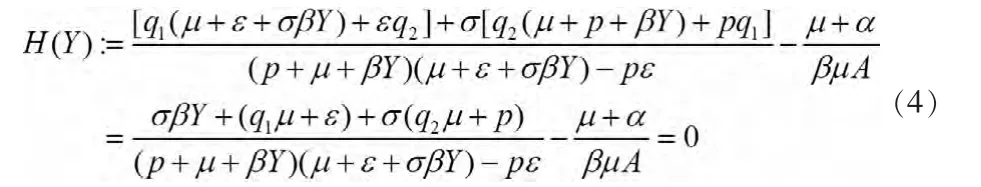
其中σ0=(p+μ)(q2μ+p)σ2+σ[p(q1μ+ε)+ε(q2μ+p)]+(μ+ε)(q1μ+ε)，

所以函数当Y＞0时，H(Y)是单调递减的。

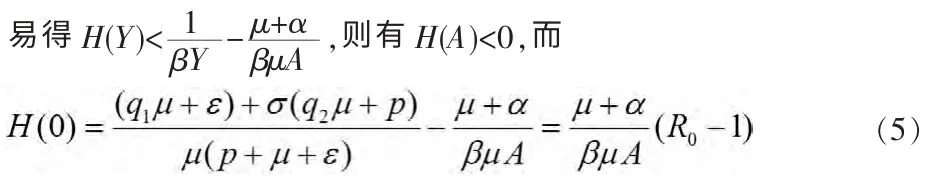
因此，由H(Y)的单调性得，当R0＞1时，H(Y)=0在区间(0,A)上存在唯一的正根；当R0≤1时在区间(0,A)上不存在正根。

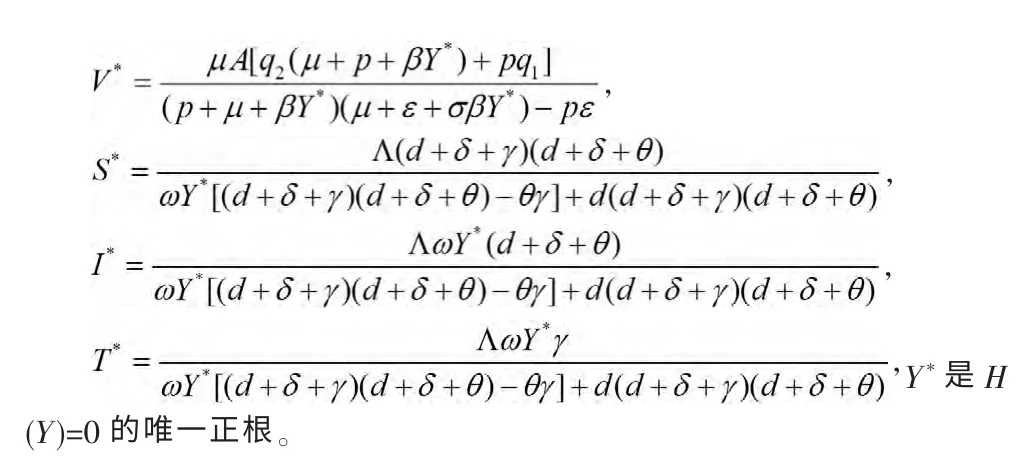
2 平衡点的稳定性

2.1 无病平衡点的稳定性

系统（1）在E0处的Jacobian矩阵为

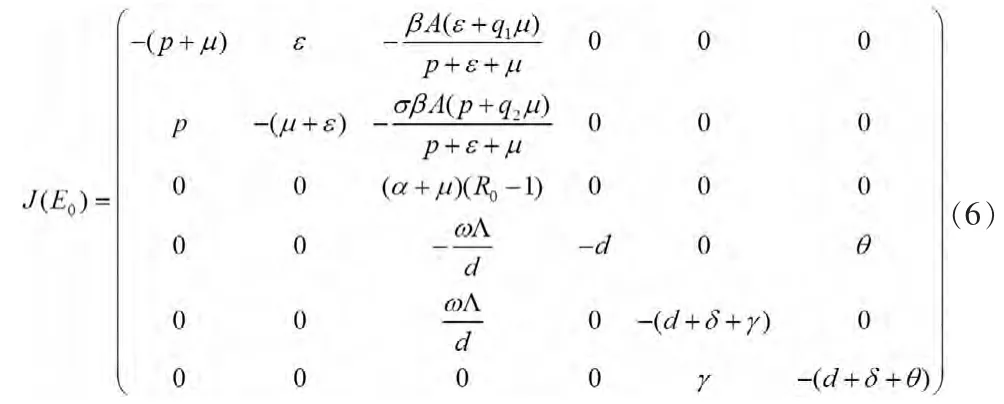
特征方程为

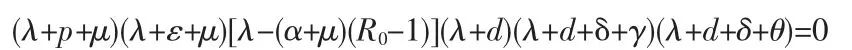
显然，该方程的根均有负实部的充要条件是R0≤1，于是得到：

定理2 当R0≤1时,则E0是局部渐近稳定的。

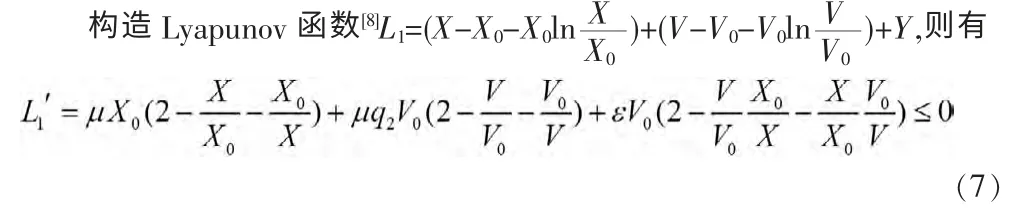
当且仅当X=X0,V=V0时，L1′=0。由Lasalle不变集原理[9]，可以得到下面的定理：

定理3 当R0≤1时,则E0是全局渐近稳定的。

2.2 正平衡点的稳定性

系统（1）在E+处的Jacobian矩阵为

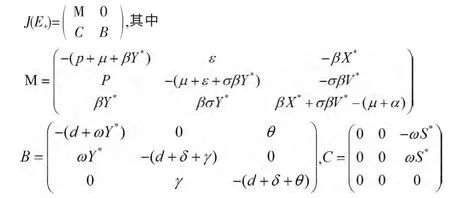
显然，J在正平衡点E+的特征值由M和B的特征值决定。很明显，矩阵B的特征根均具有负实部，而矩阵M的特征方程是

其中，

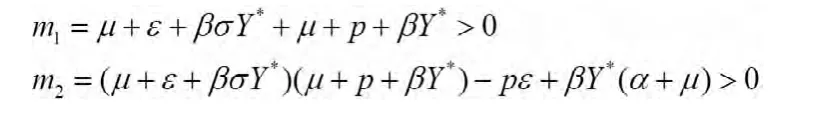
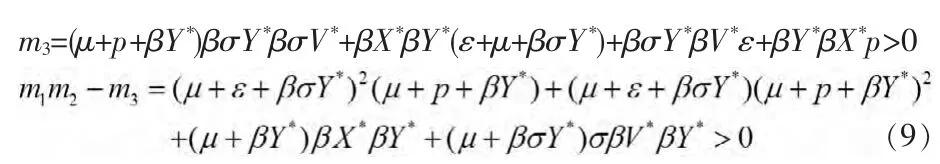
由Routh-Hurwitz判据[10]可知，矩阵M的的特征根均有负实部。于是有下面的定理：

定理4 当R0＞1时,则E+是局部渐近稳定的。

定理5 当R0＞1时,则E+是全局渐近稳定的。

3 结论

本文构造了一个具有接种免疫，并且考虑了新生个体免疫性能的SIV-SIT动力学模型，通过下一代矩阵原理得出了系统的基本再生数R0，并且运用Lyapunov函数证明了系统的全局稳定性。当R0≤1时，系统仅有一个无病平衡点E0且是全局渐进稳定的，疾病消亡；当R0＞1时，系统存在唯一的正平衡点E+且是全局渐进稳定的，疾病将持续成一种地方病。为了防止该疾病的进一步流行，需减少患病禽类与其他禽类或者人类的接触，并且增强免疫接种率，这样就可以有效的减少禽类对其他易感个体的传染，从而对禽流感的控制起到积极作用。

［1］S.C.Inyama.mathematical model for bird flu disease transmission with no bird migration[J].global journal of mathematical sciences.2009,8(2)：75-81.

［2］Mills C E,Robins J M,Bergetrom C T,Lipsitch M,Pandemic influenza：risk of multiple introductions and the need to prepare for them[J].PloSMedicine,2006,3(6)：1-5.

［3］Ferguson N M,Cummings D A T,Cauchemez S,et.al.,Strategies for containing an emerging influenza pandemic in Southeast Asia[J].Nature,2005,437：209-214.

［4］Germann T C,Kadau K,Longini Jr I M,Macken C A,Mitigation strategier for pandemic influenza in the United States[J].Eur JEpidem,2003,18：1065-1072.

［5］Shuqin Che,Yakui Xue.The stability of highly pathogenic Avian inuenza epidemic model with saturated contact rate[J].Applied Mathematics,2014,5(21)：3365-3371.

［6］Menach A Le,et al.Key strategies for reducing spread of avian influenza among commerical poultry holdings：lessons for transmission to humans[J].Proc R Soc B,2006,273：2467-2475.

［7］P.van den Driessche,J.Watmough,Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission[J].Math.Biosci,2002,180：29-48.

［8］A Korobeinikov,Lyapunov function and global stability for SIR and SIRS epidemiological models with non-linear transmission[J].Bull.Math.Biol.,2006,68：615-626.

［9］Lasalle J P.The Stability of Dynamical System[J].Regional confererce series in applied mathematics philadelphia.SIAM 1976.

［10］Horst R T.Persistence under relaxed point dissipativity(with application to an endemic model)[J].SIAM Journal on Mathermatical Analysis,1993,24(2)：407-435.