基于遗传算法的高速飞行器单回路模糊控制律

王 健 李 雪 卢光远

1.宇航智能控制技术国家重点实验室，北京100854 2. 北京航天自动控制研究所，北京100854 3. 中国航天科技集团公司，北京100048



基于遗传算法的高速飞行器单回路模糊控制律

王 健1,2李 雪3卢光远1,2

1.宇航智能控制技术国家重点实验室，北京100854 2. 北京航天自动控制研究所，北京100854 3. 中国航天科技集团公司，北京100048

针对通用高超声速飞行器的非线性模型，提出了一种单回路控制器的设计方法。控制系统由3个模糊控制器组成控制回路。基于遗传算法实现了模糊规则的自动优化，无需先验知识和训练样本。在控制飞行器轨迹、姿态和推力时，考虑了非线性动态特性、不确定性和约束。仿真表明，该方法能提供满意的鲁棒性和快速收敛的模糊规则。

高超声速；单回路；模糊控制；遗传算法

高超声速飞行器具有高度非线性动态特性，以及模型和环境不确定性，这些因素对飞行控制系统的负作用很强，因此提高鲁棒性是高超声速飞行控制的主要研究方向之一。

文献[1]结合动态逆与μ综合设计了纵向鲁棒控制器，研究了采用冲压发动机的验证飞行器。文献[2]采用基于变结构原理的动态逆方法来设计高超声速飞行器的纵向飞行控制系统。文献[3]在已知被控模型结构的条件下，探讨了神经网络动态逆方法。文献[4]基于模糊逻辑和遗传算法设计了吸气式高超声速飞行器的飞行控制系统。文献[5]针对线性多变量模型不确定系统，提出了一种终端滑模分解控制方法，可以简化高阶系统的控制器设计。文献[6]在变结构方法的基础上，提出了适用于一类时变非线性系统的模型偏差补偿控制方案，用于实现轨迹跟踪控制。文献[7]结合反馈线性化与线性二次调节器研究了高超声速飞行控制问题。

本文在现有方法的基础上，研究了由3个模糊控制器组成的单回路控制律，并基于遗传算法自动优化模糊规则。该方法可以为非线性控制对象设计控制回路，无需线性化，而且在构建模糊逻辑时，无需先验知识和训练样本。在仿真中，用大范围均匀分布的不确定性验证了性能，鲁棒性较好。

1 通用高超声速飞行器模型

本文采用NASA公开的高超声速飞行器六自由度非线性模型，它是基于风洞数据和计算流体力学建立的，适合飞行控制方法的数学仿真。该模型的纵向运动方程为[7]：

(1)

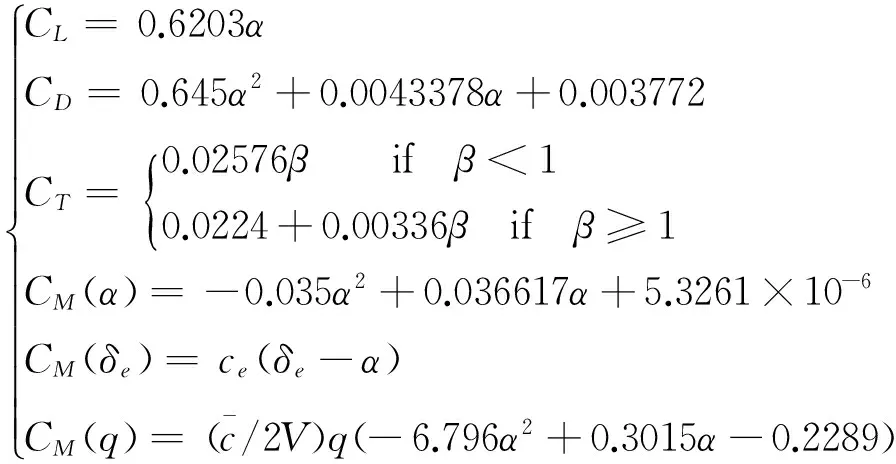
(2)

发动机二阶模型：

(3)

输入是发动机节流设置βc和升降舵偏角δe，输出是速度V和高度h。

参数不确定性用Δ表示：

(4)

2 单回路飞行控制结构

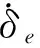
设计模糊控制器的关键是模糊规则的优化。在保证性能的前提下，减少待优化参数是加速收敛的有效措施，因此采用串联模糊控制器的方法。这是一种通过减少单个控制器的输入变量，从而减少模糊规则的方法。本文3个模糊控制器都被设计成双输入，并组成2层。第1层包括2个控制器，第2层有1个控制器。对于第1层，一个控制器输入herr及其变化率，输出一个介于-1和1之间的当量；另一个控制器输入实时攻角α及其变化率，也输出一个介于-1和1之间的当量。对于第2层的控制器，输入第1层输出的2个当量，输出发动机节流设置βc和升降舵偏角δe。

3 模糊控制器的内部结构设计

模糊控制器结构分为模糊化、数据库、规则库、模糊推理和清晰化5部分。本质上是一系列模糊数学运算，运算法则是由扎德在60年代提出的。

为了把输入的清晰量变换为模糊量，采用三角形模糊集合进行模糊化运算，隶属度函数为：

(5)

其中，a和b为待定系数，对于不同变量有所区别，依据论域范围和模糊空间分割确定。

数据库包括论域范围、模糊空间分割和隶属度函数的待定系数。

1) 论域范围

输入量：herr论域为±50m，α论域为±3°，其变化率的论域采用相同数值范围。

输出量：升降舵偏角δe论域为±10°，节流剖面设置βc论域为±0.05。

超出论域的情况按照边值处理。

2) 模糊空间分割

综合考虑控制性能和复杂程度，输入量、输出量都采用均匀分割，模糊分割级数都是11。

3) 待定系数

确定了变量论域和模糊分割以后，隶属度函数的待定系数随之确定。

将模糊控制规则库设计为标准型。规则采用状态评估形式，前、后件分别为控制器输入、输出，并基于遗传算法进行优化。

目前，模糊推理方法已经十分完备，只需指定模糊运算法则即可：与运算用求交方法，即取小；合成运算用最大-最小方法；蕴含运算用求交方法。

通过模糊推理得到模糊量后，必须将其转换成清晰量。清晰化已有多种成熟算法，本文采用加权平均法(面积重心法)：

(6)

其中，a和b是论域边界，μc(·)是语言名称c对应的隶属度函数。

4 模糊规则优化

对于模糊逻辑规则，综合考虑计算量和全局最优性，本文基于遗传算法进行参数选择。

遗传算法设定为：

1) 编码方案

采用真值编码，优点是便于全局搜索，防止陷入局部最优，改善计算复杂性，提高运算效率。

2) 适应度函数

针对跟踪问题，应用误差积分和阈值惩罚适应度函数：

(7)

(8)

3) 选择策略

应用无回放余数随机选择，该方法使得适应度优于均值的个体遗传到下一代，选择误差较小，具体操作过程是：

首先，计算群体中每个个体在下一代群体中的生存期望数目Ni：

(9)

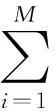
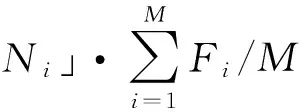
4) 遗传算子

交叉算子采用非均匀算术交叉，便于和真值编码方法结合使用。变异算子采用非均匀变异，使遗传算法在前期均匀随机搜索，在后期着重局部搜索。

5) 流程参数

综合考虑种群多样性和累积计算量，种群规模为50，算法执行最大代数为100，交叉概率取0.6，变异概率取0.1。

5 仿真

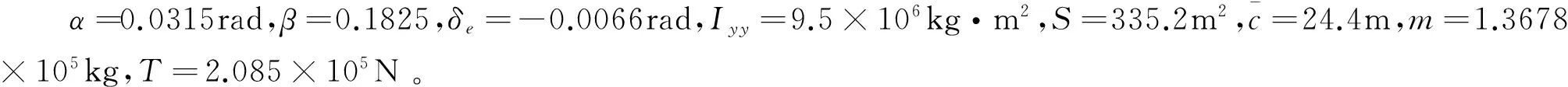
仿真验证了系统对不同高度阶跃指令的响应，加入了参数不确定性，6个随机量都服从±20%以内随机均匀分布，验证了系统的稳定性和鲁棒性。无干扰的高度阶跃响应如图1所示，有干扰的响应如图2所示。在控制规律作用下，飞行器可以准确跟踪高度指令，改变定常平飞状态，而且响应较快，没有超调。

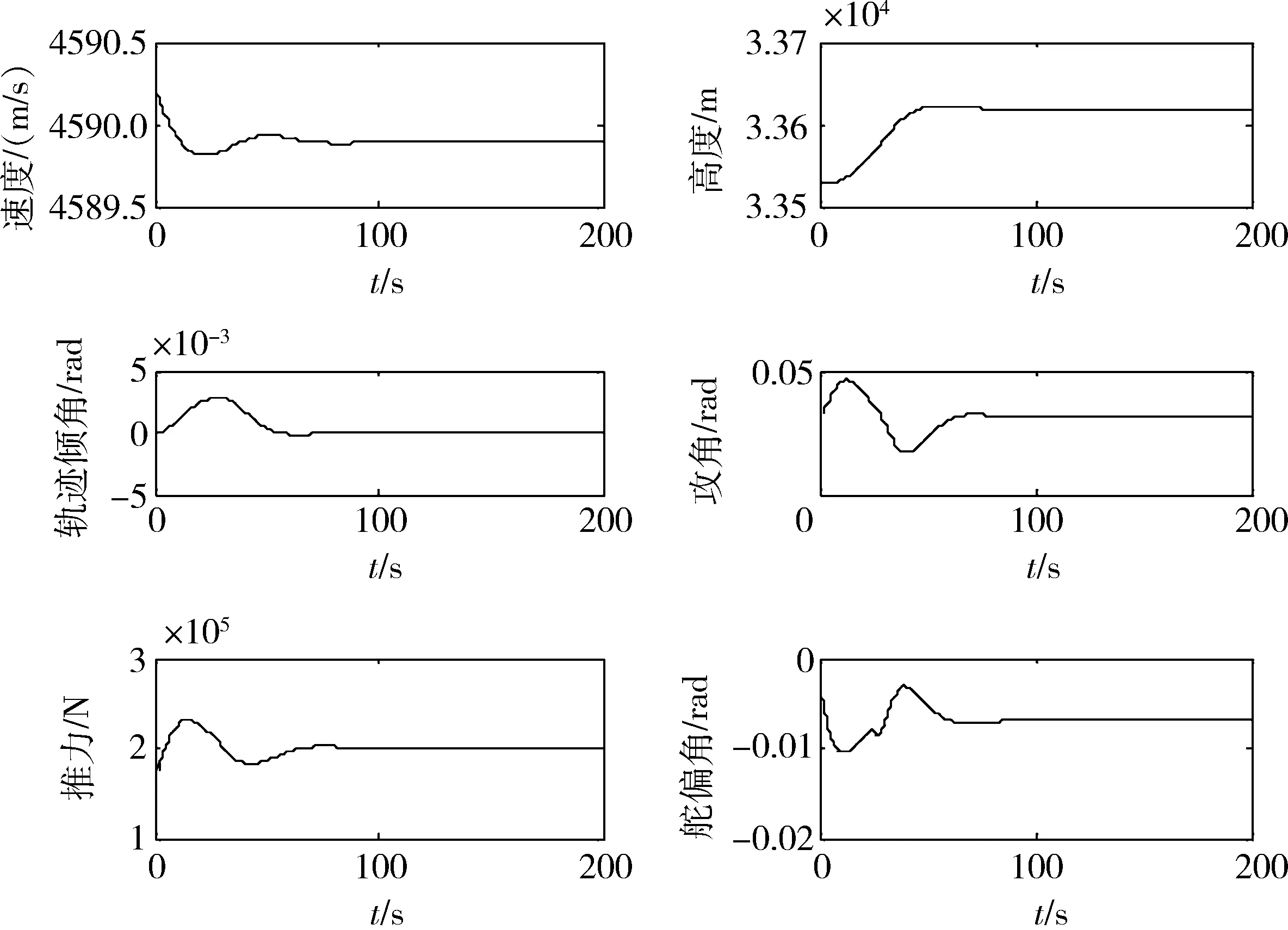
图1 系统在无干扰时对100m阶跃的响应

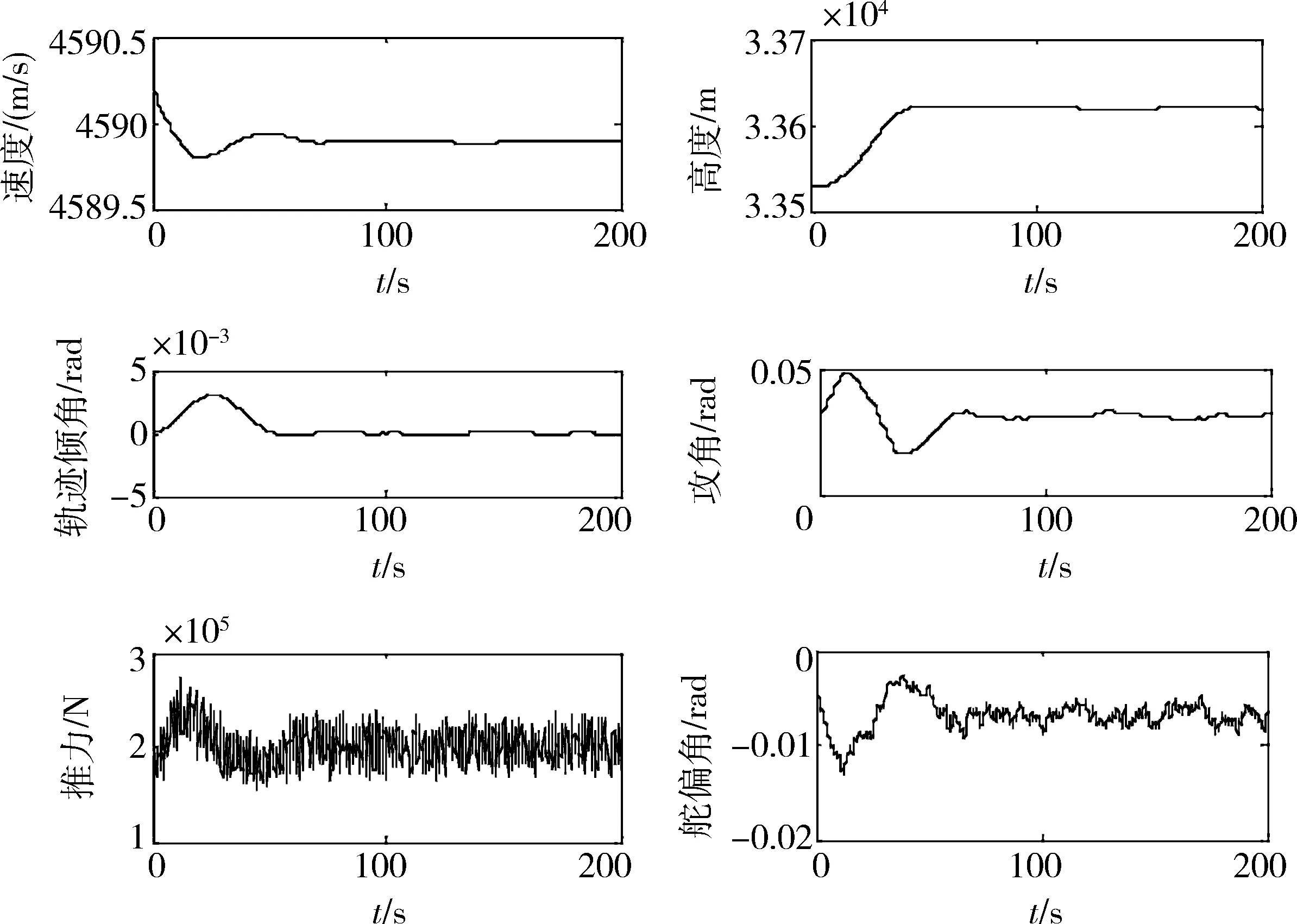
图2 系统在干扰下对100m阶跃的响应

6 结论

本文以通用高超声速飞行器为控制对象，应用模糊逻辑方法，开展了鲁棒性研究。基于串联方法组成了单回路，并通过遗传算法进行模糊逻辑控制参数优化。仿真表明，该方法能提供满意的鲁棒性、平滑的指令和快速收敛的模糊规则。

[1] Heller M, Sachs G. Flight Dynamics and Robust Control of a Hypersonic Test Vehicle with Ramjet Propulsion[R]. AIAA-98-1521, 1998.

[2] 刘燕斌，陆宇平.基于变结构理论的高超音速飞机纵向逆飞行控制[J].信息与控制，2006，35(3)：388-392.(Liu Yanbin, Lu Yuping. Longitudinal InversionFlight Control Based on Variable Structure Theory for Hypersonic Vehicle[J]. Information and Control,2006,35(3):388-392.)

[3] 李爱军，沈毅，章卫国.基于神经网络的动态逆方法研究[J].工业仪表与自动化装置，2002，(6)：7-10.(Li Aijun, Shen Yi, Zhang Weiguo. A Study on Neural Network-based Dynamic Inversion Methods[J].Industrial Instrumentation and Automation, 2002, (6): 7-10.)

[4] Kevin J Austin, B E Mechanical. Evolutionary Design of Robust Flight Control for A Hypersonic Aircraft[D].Brisbane,Australia: Department of Mechanical Engineering in University of Queensland, 2002.

[5] 冯勇，郑雪梅，鲍晟.多变量线性模型不确定系统终端滑模分解控制方法[J].控制理论与应用，2004，21(1)：11-16.(Feng Yong, Zheng Xuemei, Bao Sheng. Terminal Sliding Mode Decomposed Control of Multivariable Linear Uncertain Systems[J]. Control Theory and Applications, 2004, 21(1): 11-16.)

[6] 尤洪涛.非线性系统模型偏差补偿控制方案的研究[D].南京：东南大学自动控制系，1998.(You Hongtao. Study on Control Scheme for Model Deviation Compensation of Nonlinear System[D]. Nanjing: School of Automatic Control in Southeast University, 1998.)

[7] Wang Qian, Stengel Robert. Robust Nonlinear Control of a Hypersonic Aircraft[R]. AIAA-99-4000, 1999.

A Single-Loop Fuzzy Control Law for Hypersonic Vehicles Based on Genetic Algorithm

WANG Jian1,2LI Xue3LU Guangyuan1,2

1.National Key Laboratory of Science and Technology on Aerospace Intelligence Control, Beijing 100854, China 2.Beijing Aerospace Automatic Control Institute, Beijing 100854, China 3.China Aerospace Science and Technology Corporation, Beijing 100048, China

Accordingtothenonlinearmodelofpitchingchannelofgenerichypersonicvehicle,asingle-loopflightcontrollerisdesigned.Thesystemiscomposedofthreefuzzycontrollers.Basedonthegeneticalgorithm,theoptimizationprocessoffuzzycontrolrulesisimplementedautomaticallywithoutexpertsknowledgeandtrainingdatainadvance.Thenonlineardynamics,uncertaintiesandrestrictionsareinvolvedinresearchonthecontroloftrajectory,attitudeandthrust.Thesimulationsshowthatthemethodisabletosatisfyboththerobustnessofflightcontrolsystemandtheconvergenceofoptimizationprocessonrequest.

Hypersonic;Single-loop;Fuzzylogic;Geneticalgorithm

2013-03-12

王 健(1983-),男，山西人，工程师，主要研究方向为高速飞行器制导与控制技术；李 雪(1979-),男，北京人，工程师，主要研究方向为导航与控制；卢光远(1981-),男，黑龙江人，工程师，主要研究方向为计算机应用。

TP273+.4

A

1006-3242(2014)03-0062-04