基于全概率公式的运载火箭控制系统可靠性模型研究

胡海峰 翟邵蕾 孙海峰

北京航天自动控制研究所，北京 100854



基于全概率公式的运载火箭控制系统可靠性模型研究

胡海峰 翟邵蕾 孙海峰

北京航天自动控制研究所，北京 100854

以运载火箭典型复杂容错控制系统为研究对象，基于全概率公式和系统功能框图将复杂系统分解，推导建立了控制系统可靠性模型，给出了系统可靠性定量分析的方法和公式，并进行了计算分析。结果表明本文建模方法简单可行，对于复杂容错系统可靠性建模及定量分析具有很好的参考价值，可以在运载火箭可靠性建模分析、方案优化中推广应用。

全概率公式；运载火箭；复杂容错；飞行控制系统；可靠性模型

可靠性模型是一种概率模型，通常以概率表达式或概率分布函数的形式表示。可靠性模型包括可靠性框图和数学表达式，用以表示系统完成任务与系统组成结构的关系。建立可靠性模型是可靠性研究的基础，根据系统特点，可以有多种可靠性建模方法，如可靠性框图、网络可靠性模型、故障树模型、事件树模型、马尔可夫模型、Pe-tri网模型、GO图模型等[1]。为预计或估算产品的可靠性所建立的可靠性方框图和数学模型称为可靠性框图模型，它是对系统进行方案分析、系统优化、可靠性评估最直观和通用的方法，得到了广泛的应用[2-3]。

运载火箭控制系统可靠性定量分析和计算都是在模型上进行的，一旦系统的使用要求和功能、结构初步确定，就可以利用系统功能框图所表示的各单元之间的物理关系和信息流程，建立系统的可靠性框图，以进一步揭示系统与各单元之间的逻辑关系，并推导出系统可靠性数学模型。当控制系统采用系统级冗余并具备容错功能时，建立可靠性模型将变得异常复杂。本文基于全概率公式和系统功能框图，以典型复杂容错控制系统为研究对象进行了可靠性建模，研究推导给出了系统可靠性定量分析的公式，并进行了算例分析。

1 全概率公式简介

全概率公式是概率论中最基本和最重要的公式之一，利用全概率公式可以把复杂事件发生的概率计算问题转化为计算若干互斥的简单事件情形下该事件的条件概率以及这些情形事件发生的概率。实际问题中为了求复杂事件的概率，往往把它分解成两个或若干个互不相容的简单事件，求出这些简单事件的概率，利用加法公式求出复杂事件的概率[4]。为此引入样本空间的划分概念和全概率公式。

定义1[5]：设(Ω,F,P)为概率空间，若

Ai∈F(i=1，2，…，n)

满足

AiAj=φ(i≠j，i，j=1，2，…，n)

则称A1,A2,…,An为Ω的一个完备事件组或称为Ω的一个划分。

定理1[5]：设(Ω,F,P)为概率空间，A1,A2,…,An为Ω的一个划分，且

P(Ai)>0 (i=1，2，…，n)

则对于任一事件B∈F，有

(1)

上式称为全概率公式。显然,全概率公式给出了计算某一复杂事件B的概率的公式，只要知道使B发生的各种原因Ai发生的概率p(Ai)以及在各种原因发生的条件下B发生的条件概率P(B|Ai)，那么事件B发生的概率就可以利用全概率公式来计算。

2 复杂容错控制系统可靠性建模

2.1 复杂容错控制系统

运载火箭控制系统运行的环境条件是恶劣的，失败的损失是巨大的，对控制系统提出高可靠性要求[6]。冗余容错技术成为提高运载火箭飞行控制系统可靠性的重要手段。某型运载火箭控制系统采用图1的系统级冗余方案，为便于分析，系统模型中仅考虑箭机、惯组和综合控制器三类典型设备，全箭通过1553B总线网络连接3套完整的电气系统，形成相对独立的系统级三冗余系统。设备均为三冗余，每一套由1条双通道1553B总线连接，其中箭机和综合控制器均为3台单机冗余在1个设备中，3台单机之间通过机内总线通信。

图1 运载火箭复杂容错控制系统框图

对于惯组和BC，若3个模块均正常，则系统以三模冗余3取2表决方式工作；若其中1个模块失效，则系统通过故障检测定位将其切除，系统降级为双冗余系统；若又有1个模块失效并被定位切除，则系统以单机模式运行。对于综合控制器，其输出通过硬件实现3取2表决，可通过表决屏蔽1个故障模块；若有2个及以上模块失效，系统即失效。因此控制系统成为箭载计算机计算冗余表决、控制器指令解析冗余表决、输出级功率放大冗余表决同步、总线网络冗余的复杂冗余容错系统结构。

2.2 基于全概率公式的系统可靠性建模

在分析图1系统可靠性时，虽然每套1553B总线均有A，B双通道，当A总线出故障时可以切换为B通道，但是考虑到A，B均故障、总线协议芯片故障以及切换失败的情况，应考虑总线本身的可靠性，这相当于在系统中串联1个单元，系统功能框图如图2。

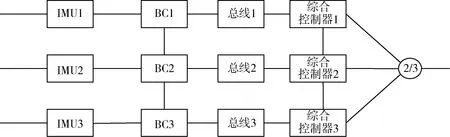
图2 控制系统功能框图

系统既非串并联又非并串联系统，而是介于2者之间的相互交叉的复杂系统，很难将其简化为简单的并联、串联等典型结构的组合。如果用状态枚举法，需要列出212种组合，计算量庞大，本文将基于全概率分解法进行控制系统可靠性建模分析，借助于全概率公式把复杂网络系统分解，直到简化为一般的串、并联系统。在具体运用全概率公式的时候，如何选择样本空间Ω的划分A1,A2,…,An尤其重要。首先以BC1，BC2和BC3的状态为条件，应用全概率公式对系统进行分解。设系统中每个单元只取正常或失效2种状态，取“1”代表单元正常，取“0”代表单元失效，则BC1，BC2和BC3的状态共有23种组合：000，001，010，011，100，101，110，111，令A表示BC1，BC2和BC3的状态组合集合，R(Ai)为BC1，BC2和BC3在Ai状态下的概率，R(S|Ai)为控制系统在Ai状态下的系统可靠性，则：

A={A1，A2，A3，A4，A5，A6，A7，A8}=

{000，001，010，011，100，101，110，111}

(2)

根据定义1，A1,A2,…,An为Ω的一个划分。根据全概率公式，控制系统可靠性计算公式如下：

(3)

其中，R(001)是BC1，BC2和BC3的状态分别为失效、失效和正常的概率；R(S|001)是BC1，BC2和BC3的状态分别为失效、失效和正常时系统正常的概率；……。

为方便计算，假设系统中各单元可靠度均为R，根据概率知识可得：

R(001)=R(010)=R(100)=R(1-R)2
R(011)=R(101)=R(110)=R2(1-R)
R(111)=R3

(4)

下面计算条件概率R(S|Ai)，其中i=1，2，…，8。

1)R(S|001)，即BC1，BC2和BC3的状态分别为失效、失效、正常时系统正常的概率。此时的功能框图如图3。

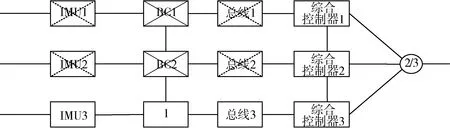
图3 BC为001状态控制系统功能框图

由于BC是系统的核心，BC失效相当于整条总线失效，因此BC1，BC2所对应的IMU1，IMU2均失效；但由于综合控制器3台单机可以通过内部双口RAM进行通讯，因此只要综合控制器3和另外1台单机正常工作(由系统冗余容错功能诊断)，输出部分即能正常。系统可靠性框图可简化如图4。

由以上分析可知：

R(S|001)=R3(2R-R2)

(5)

当BC1，BC2和BC3的状态为010，100时，情况同001类似，可得：

R(S|010)=R(S|100)=
R(S|001)=R3(2R-R2)

(6)

2)R(S|011)，即BC1，BC2和BC3的状态分别为失效、正常、正常时系统正常的概率。此时的功能框图如图5。

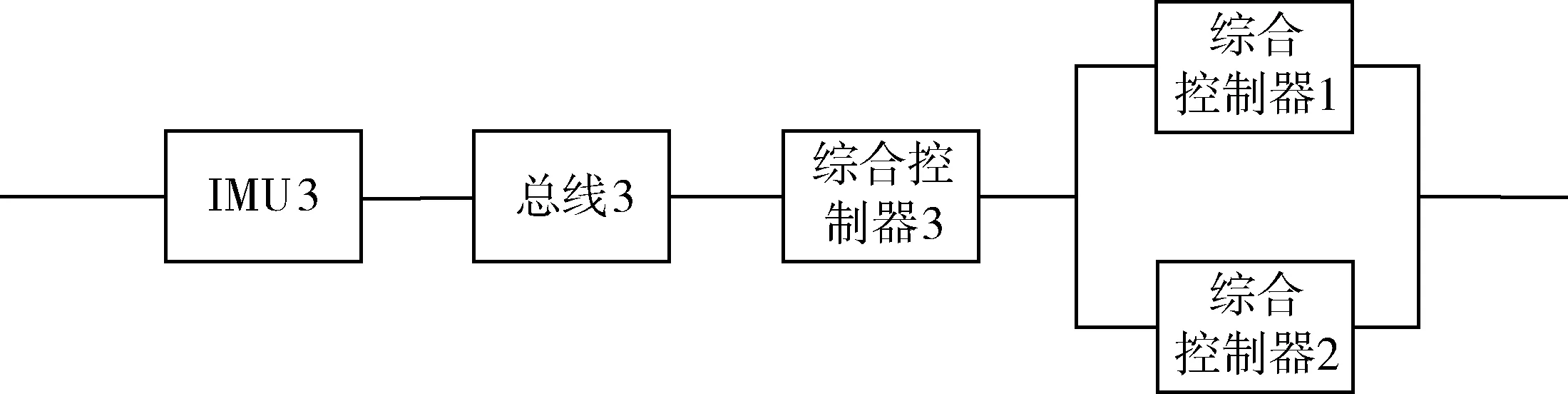
图4 BC为001状态控制系统可靠性框图

图5 BC为011状态控制系统功能框图

由框图可以看出，此时第1条总线失效，余下的系统情况仍然比较复杂，因此选择以总线2和总线3的状态为条件，基于全概率公式继续向下分解。总线2和总线3的状态共有22=4种组合，分别是：00，01，10，11，根据全概率公式可得：

R(S|011)=R(00)R(S|011,00)+R(01)
R(S|011,01)+R(10)R(S|011,10)+
R(11)R(S|011,11)

(7)

其中，R(01)表示总线2和总线3的状态分别为失效、正常的概率；R(S|011,01)表示当BC1，BC2，BC3的状态分别为失效、正常、正常，且总线2和总线3的状态分别为失效、正常时系统正常的概率；……。

则：

R(01)=R(10)=R(1-R)，R(11)=R2

(8)

求R(S|011,01)时，框图如图6。

可得：

R(S|011,01)=R2(2R-R2)

(9)

同理，可得：

R(S|011,10)=R2(2R-R2)

(10)

R(S|011,11)=(2R-R2)(3R2-2R3)

(11)

综合以上分析，可得出：R(S|011)=R(01)R(S|011,01)+R(10)R(S|011,10)+R(11)R(S|011,11)=R(1-R)R2(2R-R2)+R(1-R)R2(2R-R2)+R2(2R-R2)(3R2-2R3)=R2(2R-R2)(2R+R2-2R3)

(12)

当BC1，BC2和BC3的状态为101，110时，情况同011类似，可得：

R(S|101)=R(S|110)=R(S|011)=
R2(2R-R2)(2R+R2-2R3)

(13)

3)R(S|111)，即BC1，BC2和BC3的状态分别为正常、正常、正常时系统正常的概率。功能框图如图7。

图7 BC为111状态控制系统功能框图

仍然选择以总线1，总线2和总线3的状态为条件继续向下分解，总线1，总线2和总线3的状态共有23=8种组合：000，001，010，011，100，101，110，111，根据全概率公式可得：

R(S|111)=R(000)R(S|111,000)+R(001)R(S|111,001)+…+R(111)R(S|111,111)=
R(001)R(S|111,001)+…+R(111)
R(S|111,111)

(14)

同上面的方法，可求得R(S|111,001)，…，R(S|111,111)分别为：

R(S|111,001)=R2(2R-R2)，R(S|111,010)=R(S|111,100)=R(S|111,001)=
R2(2R-R2)，R(S|111,011)=R(S|111,101)=
R(S|111,110)=(2R-R2)(3R2-2R3)，
R(S|111,111)=(3R-3R2+R3)(3R2-2R3)。

(15)

综合以上分析，可以得出：

R(S|111)=R(001)R(S|111,001)+…+
R(111)R(S|111,111)=3R4(1-R)2(2-R)+
3R5(1-R)(2-R)(3-2R)+
R6(3-3R+R2)(3-2R)

(16)

至此，得到了全部条件概率，计算过程结果见表1。

根据全概率公式，将计算过程综合，可得系统可靠性计算模型：

表1 系统可靠性模型计算过程结果

(17)

3 可靠性计算与分析

3.1 可靠性计算

运载火箭控制系统单元模块或单机可靠度R一般不低于0.990，令R在0.990～0.9999变化，将R代入式(17)，按控制系统可靠性模型进行计算，主要计算结果见表2。

BC1，BC2和BC3共8个状态，状态为000时系统失效，其余状态可分为3类：第1类为两度故障，包括001，010，100三个状态；第2类为一度故障，包括011，101，110三个状态；第3类为无故障，即111状态。当R在0.990～0.9999变化，按BC状态分类分别统计对系统可靠性的影响，统计结果见表3。

表3 BC状态对系统可靠性的影响

根据表2和3的计算结果，系统可靠性随单元模块可靠度R(0.990～0.9999)变化的趋势图见图8，BC状态对系统可靠性的影响见图9～ 11。将BC在两度故障、一度故障状态下系统正常工作的概率与控制系统可靠性的比值进行计算，并转换为百分比，得到BC故障状态对系统可靠性的影响率，其随单元模块变化的趋势图见图12。

图8 系统随模块可靠性变化趋势图

图9 BC两度故障对系统可靠性的影响

图10 BC一度故障对系统可靠性的影响

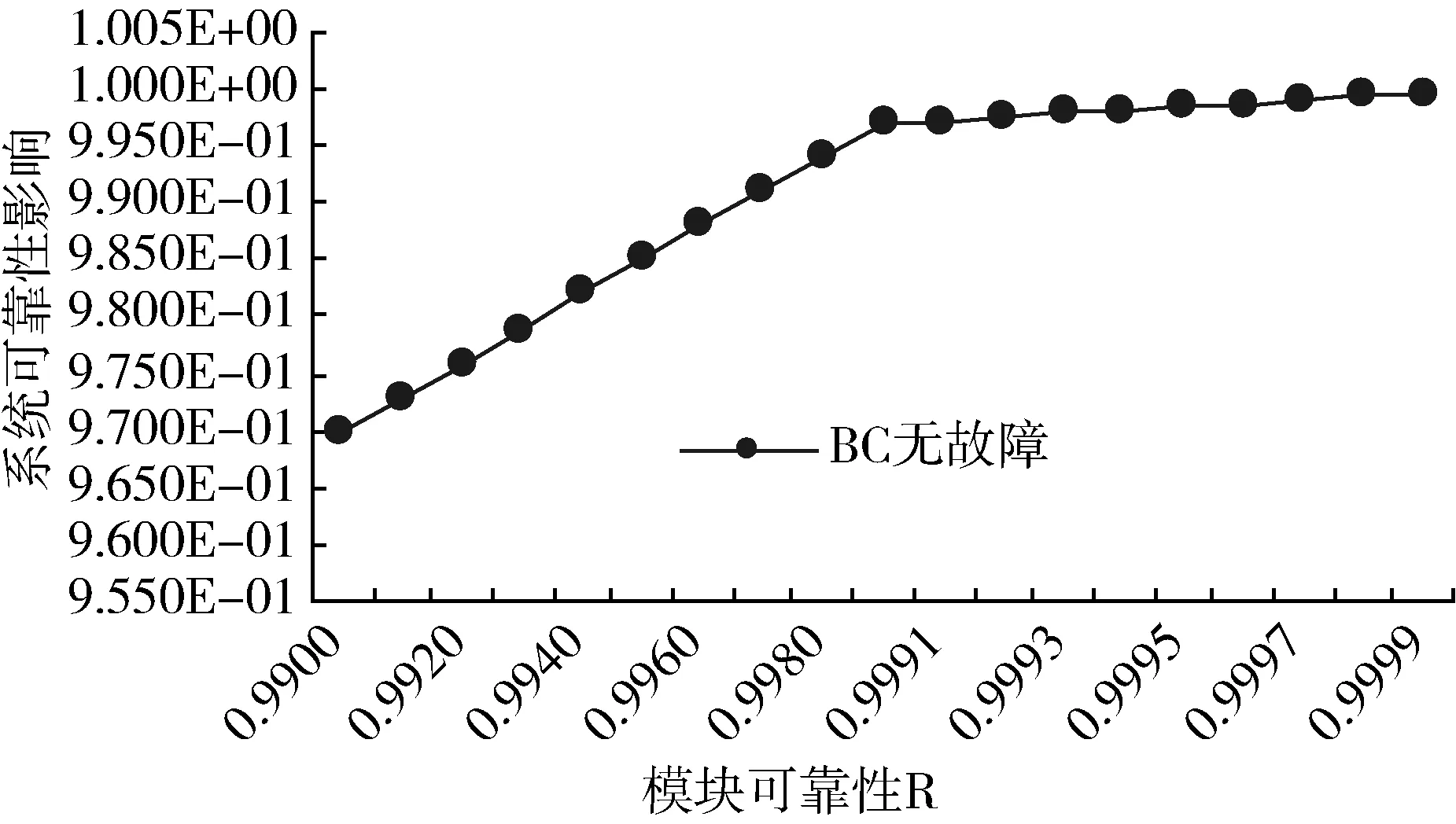
图11 BC无故障对系统可靠性的影响

3.2 分析与讨论

全概率公式本质是一种平均概率，是条件概率的加权平均，其中每个条件概率上的权重就是作为条件的事件发生的概率。在应用全概率公式进行系

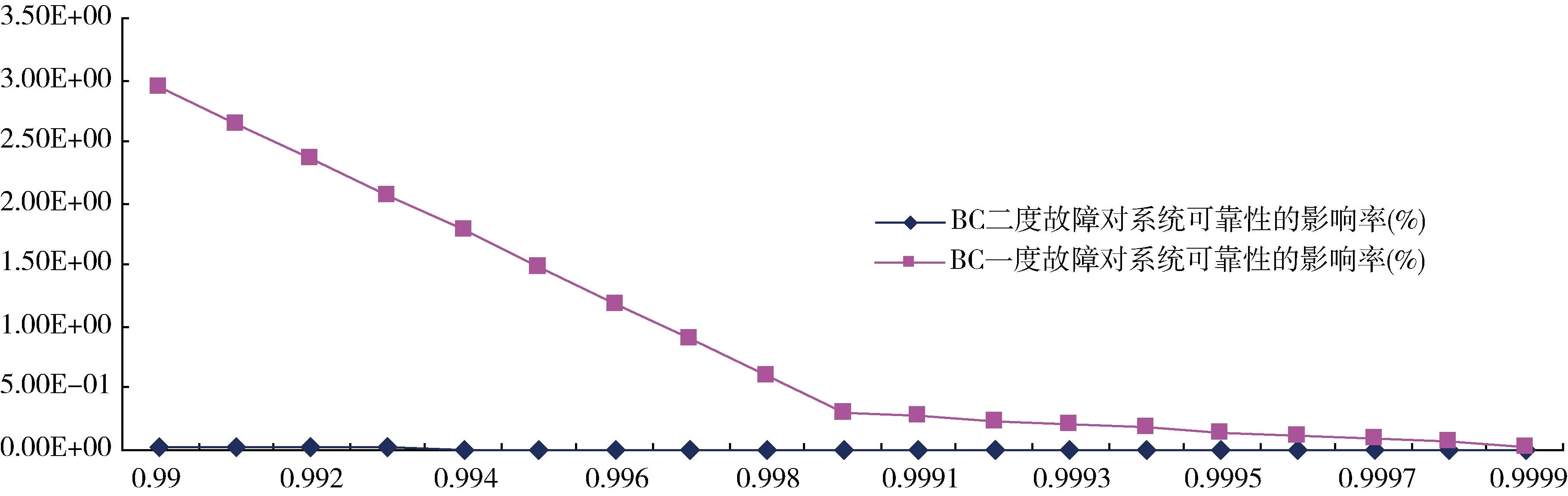
图12 BC故障状态对系统可靠性的影响率

统可靠性建模分析的时候，如何选择样本空间S的划分A1，A2,…,An显得尤其重要。在选择划分的时候，一定要把产生结果的原因全找出来，缺一不可，并且保证A1，A2,…,An为两两互不相容事件。本文选择BC的状态进行了8个划分，选择恰当的划分将会使计算大为简化。本文仅以惯组、箭机(含BC)、综合控制器、总线组成的冗余容错控制系统为研究对象进行了可靠性建模分析，并且为计算方便，将这些单元模块(或单机)的可靠性指标统一设为R，实际控制系统组成还包括伺服机构、伺服控制器、电池、配电器等设备，并且由于任务需求的差异，不同型号的控制系统组成也会有所差别，但均可以本文提供的方法为基础进行可靠性建模分析。将该方法应用到具体型号时，需在模型及框图中增加相应的设备，同时由于设计方案的复杂程度、工艺成熟性等不同，各类设备的可靠性也不同，各个设备的可靠性可分别用R1，R2，…等代替，代入到系统功能框图和可靠性模型中，最终得到全系统的可靠性模型，并基于模型进行系统可靠性分析、评估和设计。

4 结束语

全概率公式提供了计算复杂函数概率的有效途径，本文以简化的运载火箭冗余容错控制系统为研究对象，基于全概率公式进行了样本空间划分，推导建立了复杂容错系统可靠性计算模型，给出了可靠性定量分析的公式，并对可靠性模型进行了计算分析。为便于建模和计算，对研究对象进行了简化，提供的是一种复杂容错控制系统可靠性建模通用的方法，在型号中应用时，可以基于该方法根据具体组成和设备可靠性水平建立系统可靠性模型，并进行可靠性分析、评估和设计。该法对于运载火箭复杂冗余容错控制系统可靠性建模及定量分析具有很好的参考价值，可以推广应用。

[1] 曾声奎，赵廷弟，等.系统可靠性设计分析教程[M].北京：北京航空航天大学出版社，2001.(Zeng Shengkui, Zhao Tingdi, et al. The System Reliability Design and Analysis Tutorial [M]. Beijing: Beihang University press, 2001).[2] 朱士友.架控制动系统可靠性模型研究[J].铁道机车车辆,2012,32(3):80-83.(Zhu Shiyou. Research on Reliability Model of Shelves Control Braking System[J]. Railway Locomotive&Car, 2012,32 (3): 80-83).

[3] 李军,刘君华.多传感器融合系统的可靠性模型研究[J].西安交通大学学报，2004,38(8):775-778.(Li Jun, Liu Junhua.Study of Reliability Model for the Multi-Sensor Fusion System[J]. Jouranl of Xi’an Jiaotong Uuiversity, 2004,38(8):775-778).

[4] 马晓丽, 张亮.全概率公式的推广及其在保险中的应用[J].高等数学研究,2010,13(1):70-71.

[5] 杨振明.概率论[M].2版.北京:科学出版社,2004:34。

[6] 孙凝生.冗余设计技术在运载火箭飞行控制系统中的应用(一) [J].航天控制，2003,(1)：65-81.(Sun Ningsheng. The Redundancy Designs for Guidance and Control System of Launch Vehicle[J]. Aerospace Control, 2003, (1)：65-81).

[7] 孙凝生.冗余设计技术在运载火箭飞行控制系统中的应用(二) [J].航天控制，2003,(2)：68-80.(Sun Ningsheng. The Redundancy Designs for Guidance and Control System of Launch Vehicle[J]. Aerospace Control, 2003, (2)：68-80).

Study on Reliability Model of Launch Vehicle GNC System Based on Total Probability Formula

HU Haifeng ZHAI Shaolei SUN Haifeng

Beijing Aerospace Automatic Control Institute, Beijing 100854，China

Thetypicallaunchvehicleguidancenavigationandcontrol(GNC)systemwhichisredundantandfaulttolerantisstudied.Thiscomplexsystemisdecomposed，whichisbasedontotalprobabilityformulaandsystemfunctiondiagram.Andthen,itsreliabilitymodelisdeduced,andthequantitativeanalysismethodandformulasofthissystemareproposed，whichareusedtocalculateandanalyzesystemreliability.Theconclusionsaredrawnthatthemethodissimpleandfeasibleandithasgreatreferencedvalueonbuildingreliabilitymodelandreliabilityquantitativeanalysisofcontrolsystemwhichiscomplexandfaulttolerant.Thestudyresultscanbeextensivelyappliedtobuildingreliabilitymodelandoptimizingsysteminlaunchvehicledesign.

Totalprobabilityformula;Launchvehicle;Complexandfaulttolerant;Guidancenavigationandcontrolsystem;Reliabilitymodel

2013-08-21

胡海峰(1978-)，男，河北保定人，硕士，高级工程师，主要研究方向为运载火箭控制系统设计；翟邵蕾(1982-)，女，河北深泽人，硕士，工程师，主要研究方向为运载火箭控制系统设计；孙海峰(1976-)，男，河北吴桥人，硕士，工程师，主要研究方向为运载火箭控制系统设计。

TP274.4

A

1006-3242(2014)03-0087-08