一种利用小波分析进行航迹相关性判断的方法研究

范云锋 惠 轶 邱令存

上海机电工程研究所，上海201109



一种利用小波分析进行航迹相关性判断的方法研究

范云锋 惠 轶 邱令存

上海机电工程研究所，上海201109

对多传感器多目标的航迹相关性判断问题进行了讨论，利用小波分析的方法对航迹数据进行了多层次的分析，并充分利用了小波变换良好的去噪性质。建立了一种新型的航迹相关性判断方法，该方法能够从航迹的整体走势和局部细节2个方面综合判断航迹的相关性。仿真试验表明了该方法的可行性和有效性。

航迹相关；小波分析；整体走势；局部细节

对某一空域进行观察监视，往往是使用多部雷达或多种传感器对该空域进行扫描。由于不同传感器的精度、观测噪声等因素的不同，造成它们对同一目标的测量航迹往往不能完全重合，因此航迹相关性判断是多传感器多目标跟踪领域的一项关键技术，是数据融合的基础。只有识别出哪些观测数据序列来自同一目标，才能进行后续的融合处理。

而在以往的处理方法中，加权法和修正法仅在目标比较稀疏时效果较好，双门限法不能直接推广到多局部节点的情况，序贯法[1-4]的计算相对比较复杂，基于模糊数学[5-6]的相关方法在隶属函数的选取和规则的制定方面也没有严格的理论指导。

近年来，小波理论以其多尺度多分辨特性在诸多领域备受关注，并得到了广泛应用。本文结合小波分析的多分辨特性和良好的去噪能力，由粗到精，从航迹的整体走势和局部细节建立了航迹相关性判断的方法。

1 小波分析理论

与傅里叶变换相比，应用小波变换进行时频分析能够同时反映信号在时间域和频率域上的局部性质。小波分析方法在低频部分具有较高的频率分辨率和较低的时间分辨率，在高频部分具有较高的时间分辨率和较低的频率分辨率[7]，因此小波变换对信号具有自适应性。目标的航迹数据序列实际上是一个非平稳随机过程，在航迹的特征向量中，低频部分反映了航迹的整体走势，高频部分反映了局部细节和噪声干扰。所以可以利用小波分析的上述性质完成目标航迹在整体走势和局部细节上的相关性判断。

设信号f(t)∈L2(R)，可以将它分解为细节部分W1和大尺度逼近部分V1，接着可以将大尺度逼近部分进一步分解为W2和V2，如此重复就能得到任意尺度(分辨率)上的逼近部分和细节部分。而且，上述过程是可逆的，即只要知道Vj和Wj,Wj-1,…,W1便可以重构得到f(t)，即如式(1)所示：

(1)

在实际应用中，通常将尺度函数和小波函数进行离散化处理，以减少小波变换后的信息冗余。以二进离散小波变换为例，其尺度函数和小波函数的定义分别为：

(2)

2 航迹的低频信息相关性准则

所谓的航迹低频信息，即为对航迹数据进行小波分解后最终得到的逼近部分，可通过尺度函数系数得以反映，它能反映航迹的整体走势。

假设X1(t)和X2(t)为2个不同的传感器对同一个目标的观测曲线，且已在空间和时间上进行了对准，则可以使用Mallat快速算法[8-9]分别对X1(t)和X2(t)进行多尺度小波变换，得到尺度函数系数CX1和CX2，尺度函数系数就能表征信号的概貌。因此，判断两条航迹的整体走势是否相同，就是对2条航迹序列的尺度函数系数进行比较。因此，可采用如式(3)所示的判断准则：

(3)

在此，应用小波变换进行航迹低频信息的相关性判断时，还有一些问题需要考虑。首先是对航迹序列长度的确定，它既要满足小波分析的需要，又要使算法的数据处理量不至于太大。为了保证在每一层分解的过程中，数据的长度大于或等于所用滤波器的支撑长度，数据长度应该满足：

L≥2N-1×M

(4)

其中，L为序列的长度；M为所选择小波的滤波器的支撑长度。在处理的开始阶段数据点数不足的情况下，可采用传统的判断方法，当送来的航迹点数达到要求的长度时，转而采用小波变换的方法，并以滑窗的形式进行后续处理。

另外，式(4)中M的大小与所选择的小波函数密切相关，而且同一个工程问题，选择不同的小波函数进行分析时，结果有时相差甚远。通过文献和仿真试验发现，选择db3小波函数进行3层分解的效果较好。

3 航迹的高频信息相关性准则

所谓航迹高频信息，即为对航迹数据进行小波分解后得到的各个尺度上的逼近部分，可通过小波函数系数得以反映，它包含了航迹的细节信息和噪声。

3.1 去噪处理

如果对X1(t)和X2(t)进行多尺度小波变换后，得到的各尺度上的小波系数向量可以表示为：

(5)

为了使上述向量能够充分体现航迹的细节信息，就需要对其进行滤波处理，去除噪声带来的干扰。为此，本文引入相邻尺度系数积作为显著性函数[10]，利用有用信号在相邻尺度间的相关性，使有用信号能够积累，便于与噪声分离。相邻尺度系数积的定义如式(6)所示：

(6)

其中，l表示参与乘积运算的尺度数；j为起始尺度。由于信号突变部分的宽度会随尺度的增大而增大，以至于相邻突变点在粗尺度上会相互影响，因此一般可以取l=2，则：

Pj,2f(n)=WTjf(n)·WTj+1f(n)

(7)

用ω(t)表示高斯噪声，则其小波变换系数WTjω(t)仍然服从高斯分布，可用“3σ准则”确定作用于小波系数WTjω(t)的阈值，而作用于噪声的相邻尺度积系数的阈值还需要进一步分析。

记噪声的相邻尺度积系数为

Yj=WTjω·WTj+1ω

(8)

令

(9)

定义以下2个随机变量

(10)

可知，Yj,+和Yj,-均服从高斯分布，分别记为：

因此，可以将非高斯分布的Yj转化为Yj,+与Yj,-的函数

Yj=(Yj,+)2-(Yj,-)2

(11)

假设j尺度上的相邻尺度积系数的阈值为ts(j)，那么这时有

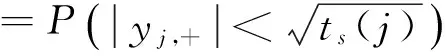
(12)

由于Yj,+服从高斯分布，可根据“3σ准则”取ts(j)≥(3σj,+)2，则

(13)

从上式可以看出，阈值的选择仅与随机变量Yj,+的统计特性有关，即只要确定了σj,+的大小，就能够确定阈值的大小。

根据式(10)可知

(14)

假设h(n)和g(n)分别表示正交离散小波的低通分解滤波器和高通分解滤波器，hj表示在h(n)的2个相邻系数间插入了2j-1个0后的结果。同理，gj表示在g(n)的2个相邻系数间插入2j-1个0后的结果。定义一个变量qj

qj=h0*h1*…*hj-2*gj-1

(15)

如果σ2为原始噪声的方差，那么由文献[11]可知，每个尺度上的噪声方差和相邻尺度上的相关系数分别为

(16)

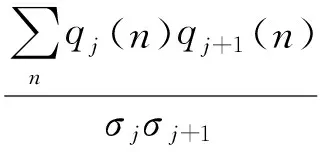
(17)

由此，计算出阈值ts(j)的大小后，便可以在每个尺度上应用硬阈值滤波方法来去除噪声，得到阈值处理后的小波系数向量为：

(18)

3.2 判断准则

给定小波函数ψ∈L2(R)，a>1和b>0是常数。定义

ψj,k:=aj/2ψ(aj·-bk)j,k∈Z

(19)

如果{ψj,k:j,k∈Z}构成L2(R)的框架，即存在2个正常数A和B使得

(20)

则称之为一个小波框架[10,12]。A和B分别为框架下界和上界。此时，任何f∈L2(R)可以由它的离散小波系数{〈f,ψj,k〉:j,k∈Z}完全重构。

利用上述小波框架条件，令f(t)=X1(t)-X2(t)，代入式(20)可得

(21)

因此，建立航迹高频信息相关性准则为：

(22)

(23)

那么

(24)

(25)

因此，只要给定检验水平α，就可以获得高斯分布的某一门限δ，并且由式(24)可以得到

(26)

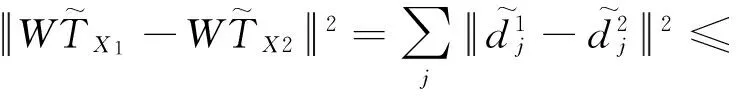
(27)

4 仿真分析

表1 目标初始状态

表1为想定的5批目标的初始位置和速度，表2为相应的运动方式，这些目标的机动航迹将多次出现相交的情形。图1给出了最终的计算结果。

由图1所示的仿真结果可以看出，与传统的加权法相比，小波分析方法的引入，确实能够提高航迹相关性判断的正确判断概率。这主要是由以下2方面因素引起的：

表2 目标运动方式

图1 机动目标的正确相关性判断概率曲线

1) 小波分析的方法能够有效地去除高频噪声的对判断结果的干扰；

2) 小波分析的方法能够分别从整体走势和局部细节来判断航迹的相关性，其中对局部细节的判断，能够根据目标的机动方式来确定航迹间的相关性，这在航迹间出现较多交叉情况时会显得尤为重要。

5 结束语

航迹的相关性判断是进行航迹融合的基础，本文以小波分析方法为工具，建立了一种新的航迹相关性判断方法。该方法首先判断航迹的整体走势，然后判断航迹的局部细节，并且在此过程中还充分利用了小波变换良好的滤波特性。从仿真结果可以看出，该方法对机动航迹具有较好的适应性。

对于非机动航迹而言，本文所提出的高频信息相关性判断实际上是可以省略的，因为此时的高频信息几乎完全是由噪声引起的。故只需要判断航迹的低频信息，即航迹的整体走势相同，那么它们就是相关的，这样将有效地降低算法的复杂程度。因此，如何识别出目标的机动，将成为后续的研究重点。

[1] 何友，王国宏，陆大琻，等.多传感器信息融合及应用[M].第二版.北京：电子工业出版社，2007：129-136.(He You, Wang Guohong, Lu Dajin, et al. Multisensor Information Fusion With Applica-tions[M]. Second Edition. Beijing: Publishing House of Electronics Industry,2007:129-136.)

[2] 秦卫华，胡飞，蔡小斌.基于递推加权最小二乘法的多目标跟踪算法[J].计算机测量与控制，2005，13(8)：840-842.(Qin Weihua, Hu Fei, Cai Xiaobin. Multitarget Tracking Algorithm on the Recursively Weighted Least Square Rule[J]. Computer Measurement & Control,2005,13(8):840-842.)

[3] 刘熹，尹浩，刘海燕，等.基于离散小波变换的航迹——航迹关联算法[J].军事运筹与系统工程，2010，24(4)：46-51.(Liu Xi, Yin Hao, Liu Haiyan, et al. A Track Correlation Algorithm Based on Discrete Wavelet Transform[J]. Military Operations Research and System’s Engineering,2010,24(4):46-51.)

[4] 李相平，章力强，应涛，等.多传感器航迹关联算法研究[J].制导与引信，2010，31(4)：12-15.(Li Xiangpin, Zhang Liqiang, Ying Tao, et al. Research on the Track Correlation Algorithm Based on the Multisensor[J]. Guidance & Fuze,2010,31(4):12-15.)

[5] 杨力，刘金梅，王茂安.基于目标预测值模糊化的模糊数据关联算法[J].探测与控制学报，2008，30(3)：72-76.(Yang Li, Liu Jinmei, Wang Maoan. Fuzzy Data Association Algorithm Based on Fuzzed Target Forecasted Value[J]. Journal of Detection & Control,2008,30(3):72-76.)

[6] 刘德浩，王国宏，陈中华.系统误差下的模糊航迹关联方法[J].现代防御技术，2012，40(3)：128-131.(Liu Dehao, Wang Guohong, Chen Zhonghua. Fuzzy Track Alignment-Correlation Algorithm with Systematic Error[J]. Modern Defence Technology,2012,40(3):128-131.)

[7] 刘诗华，徐毓，金宏斌.基于小波变换的双门限航迹关联算法[J].计算机测量与控制，2004，12(6)：563-565.(Liu Shihua, Xu Yu, Jin Hongbin. Algorithm for Double Threshold Track Correlation Based on Wavelet Transform[J]. Computer Measurement & Control,2004,12(6):563-565.)

[8] Mallat S.A Theory for Multiresolution Signal Decomposition: The Wavelet Respre-sentation[J].IEEE Trans on PAMI，1989，11(7)：674-693.

[9] 芮国胜，康健.小波与傅里叶分析基础[M].第二版.北京：电子工业出版社，2011.(Rui Guosheng, Kang Jian. A First Course in Wavelets with Fourier Analysis[M]. Second Edition. Beijing: Publishing House of Electronics Industry,2011.)

[10] 孟晋丽.基于领域相关性的小波域滤波算法研究[D].西安：西北工业大学博士学位论文，2006.(Meng Jinli. Wavelet Denoising Based on Adjacent Dependencies[D].Xi’an: A Dissertation for the Degree of Philosophy Doctor.)

[11] Pan Quan, Zhang Lei, Dai G Zh,et al. Two Denoising Methods by Wavelet Transform[J]. IEEE Transactions on Signal Processing,1999,47(12):3401-3406.

[12] 徐毓，金以慧.基于多尺度小波变换和短时分形理论的航迹关联方法[J].控制与决策，2003，18(4)：432-435.(Xu Yu, Jin Yihui. Target Tracks Association Based on Multi-resolution Wavelet Transform and Short-time Fractal[J]. Control and Decision,2003,18(4):432-435.)

A Method for Track Correlation Estimation Based on Wavelet Analysis

FAN Yunfeng HUI Yi QIU Lingcun

Shanghai Electro-Mechanical Engineering Institute, Shanghai 201109, China

Theproblemoftrackcorrelationformulti-sensorandmulti-targetisdiscussed.Thewaveletanalysis,whichhashighdenoisingquality,isusedtoanalyzetrackdata.Anewtrackcorrelationalgorithmispresented.Thetrackcorrelationcanbedeterminedwithoveralltrendandlocaldetailoftracksbyusingthismethod.Thesimulationresultsshowthatthisalgorithmiseffective.

Trackcorrelation;Waveletanalysis;Overalltrend;Localdetail

2013-03-12

范云锋(1988-),男，湖北宜昌人，硕士研究生，主要研究方向为指挥控制通信系统设计；惠 轶(1974-),男，黑龙江黑河人，研究员，主要研究方向为武器系统总体设计；邱令存(1976-)，男，山东泰安人，高级工程师，主要研究方向为指挥控制通信系统设计。

TP391.41

A

1006-3242(2014)03-0003-04