一种基于自适应控制分配的飞行控制方法
张之瑶 黄万伟 柳嘉润
北京航天自动控制研究所,北京100854
一种基于自适应控制分配的飞行控制方法
张之瑶 黄万伟 柳嘉润
北京航天自动控制研究所,北京100854

为保障多操纵面飞行器的安全性,提升飞行性能,提出了一种基于自适应控制分配的新型飞行控制方法。首先,阐述了用非线性动态逆设计多层飞行控制律的思想;然后,将与操纵效率相关的模糊罚函数引入到二次规划动态控制分配方法中,使控制分配的优化方向对于操纵效率的变化具有自适应能力,形成了自适应动态控制分配算法;最后,通过无故障三轴姿态控制仿真和故障存在情况对比仿真,验证了该方法的有效性和优越性。
自适应控制;控制分配;多操纵面;动态逆;二次规划
经典的大气层内面对称有翼飞行器的飞行控制系统是基于传统的三通道设计,单独的操纵面控制单一方向的力矩。为了获得更高的机动性、操纵性和可靠性及其它控制目标,现代先进飞行器结构设计大多采用多个独立的操纵面,使其具有较高的控制冗余度,即使某操纵面发生故障,仍然能通过其它正常操纵面的重新组合进行协同控制, 提高飞行器对故障及损伤的鲁棒性[1]。
由于控制面耦合程度的增强,如何有效地将控制指令分配到冗余的、受位置和速率约束的操纵面上,就成为控制系统设计首先要考虑的控制分配问题。早期的控制分配技术是从上世纪80年代中期美国的自修复研究计划中发展起来的,这一时期主要是对伪逆法的研究,因为这种方法具有结构和计算简单、重构速度快的特点,逐渐成为 90年代自修复技术的工程应用方法。由于现代高性能有翼飞行器的多操纵面特性,使得控制分配问题不再局限于自修复领域,而成为飞行控制系统设计的一个必不可少的环节。作为飞控系统设计的重要部分,将控制分配技术单独进行研究,可以将标准的飞控系统设计转化为模块化飞控系统进行设计,它与飞行控制律结合在一起共同解决复杂的多操纵面飞行控制系统解耦控制问题。
对于控制分配技术,国内外的科研工作者取得了很多研究成果,具体可归纳为2大类:基于优化的分配法和非优化的分配法。基于优化的方法主要包括广义逆法和基于线性规划的直接几何方法,以及基于二次规划的动态分配法;非优化控制方法主要包括直接几何法和串接链控制分配法。该技术是解决冗余控制量最优分配的有效方法,已被广泛应用于先进战斗机、导弹、 航天器等航空航天领域。然而,飞行器各操纵面的控制作用和控制程序是不同的,且不同操纵面偏转引起气动布局的变化对飞行器的控制效能都会产生影响。如何以最有效的组合实现最快、最大限度的控制目标,使飞行器的性能得到最大的发挥,是控制算法必须解决的问题。
现代飞行控制技术对上述问题的解决方式是将控制器分解为独立的控制律模块和控制分配器,如图1所示。

图1 带独立控制分配器的模块化控制结构
由控制律模块产生三轴期望力矩或角加速度,经控制分配器解算处理,形成控制操纵面的位置指令,然后各执行机构跟踪这些位置指令获得所要求的控制力矩或角加速度。该做法使分配器与控制律的设计相互独立:①简化了控制器设计过程,可采用多种成熟的飞行控制设计方法;②在某操纵面出现故障失效时, 可仅通过调整分配器实现重构,无须对控制律进行调整,还可直接处理控制量的约束问题, 包括位置和速率约束。
目前国内外控制分配算法主要可分为4类:广义逆算法、链式递增算法、直接分配算法和数学规划算法[2-6]。如何将这些算法进行改进以提高控制分配算法应对伺服特性变化(包含故障)的能力,已成为近年来的主要研究方向[7-9]。
本文提出了一种基于自适应控制分配方法的新型飞行控制方法,采用非线性动态逆方法设计了分层飞行控制律,并且将反映操纵面操纵效率的自适应因子引入到二次规划动态分配算法,从而形成对操纵面故障具有容错能力的新型控制方法。仿真验证了该方法的有效性和优越性。
1 动态逆飞行控制
非线性动态逆方法是直接基于非线性对象进行设计的一种方法。该方法的实质就是通过全状态反馈和Falb-Wolovich矩阵求逆将原仿射非线性系统补偿成为具有线性传递关系的系统,即伪线性系统;然后再用线性系统的理论完成这种系统的综合。这就可以实现在线性系统中诸如解耦、极点配置、二次型指标最优、鲁棒伺服跟踪等目标。动态逆方法要求系统的输入和输出变量数目相同,在应用于飞行控制时,需要利用奇异摄动理论降阶进行分层降阶控制。
由于多操纵面飞行器飞行状态量具有明显的时间尺度差异,使飞行控制系统能够满足分层控制的条件。因此,可将状态变量分为以下几个层次:
1) 快变量,如角速率p,q,r;
2) 慢变量,如攻角α、侧滑角β及速矢倾侧角μ;
3) 很慢变量,如速度V、航向角χ和轨迹倾角γ;
4) 极慢变量,如高度h等。
这样,按照时间尺度的划分,一个完整的动态逆飞行控制回路结构就由4层回路嵌套而成,如图2所示。

图2 动态逆飞行控制回路结构
2 适应控制分配方法
2.1 控制分配问题描述
图2所示的4层动态逆飞行控制回路将向控制面管理器输出飞行控制所需的期望三轴控制力矩,控制面管理器负责最内层的控制工作,即根据飞行器冗余操纵面的总体和气动特性、实时工作状态来实时进行控制分配,以达到减小总操纵面偏转量、推迟操纵面饱和、提高伺服系统可靠性和降低能耗的作用。
若只考虑所产生的瞬时力矩,并假设各操纵面作用相对独立且可以线性化,则可将操纵面控制分配问题描述如下:
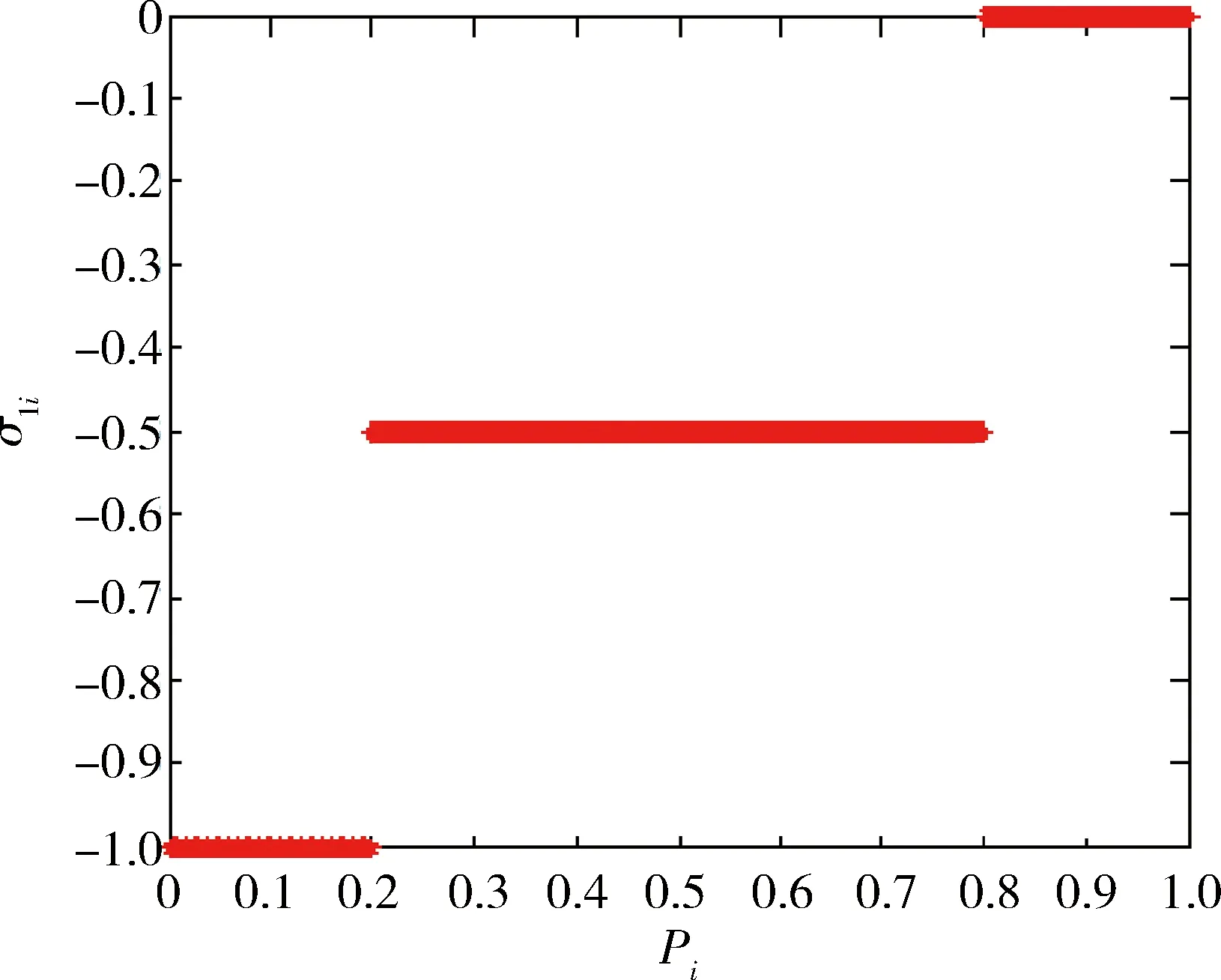
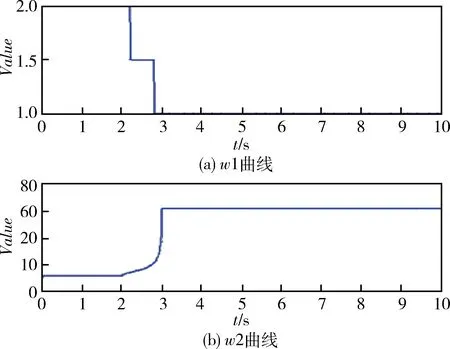
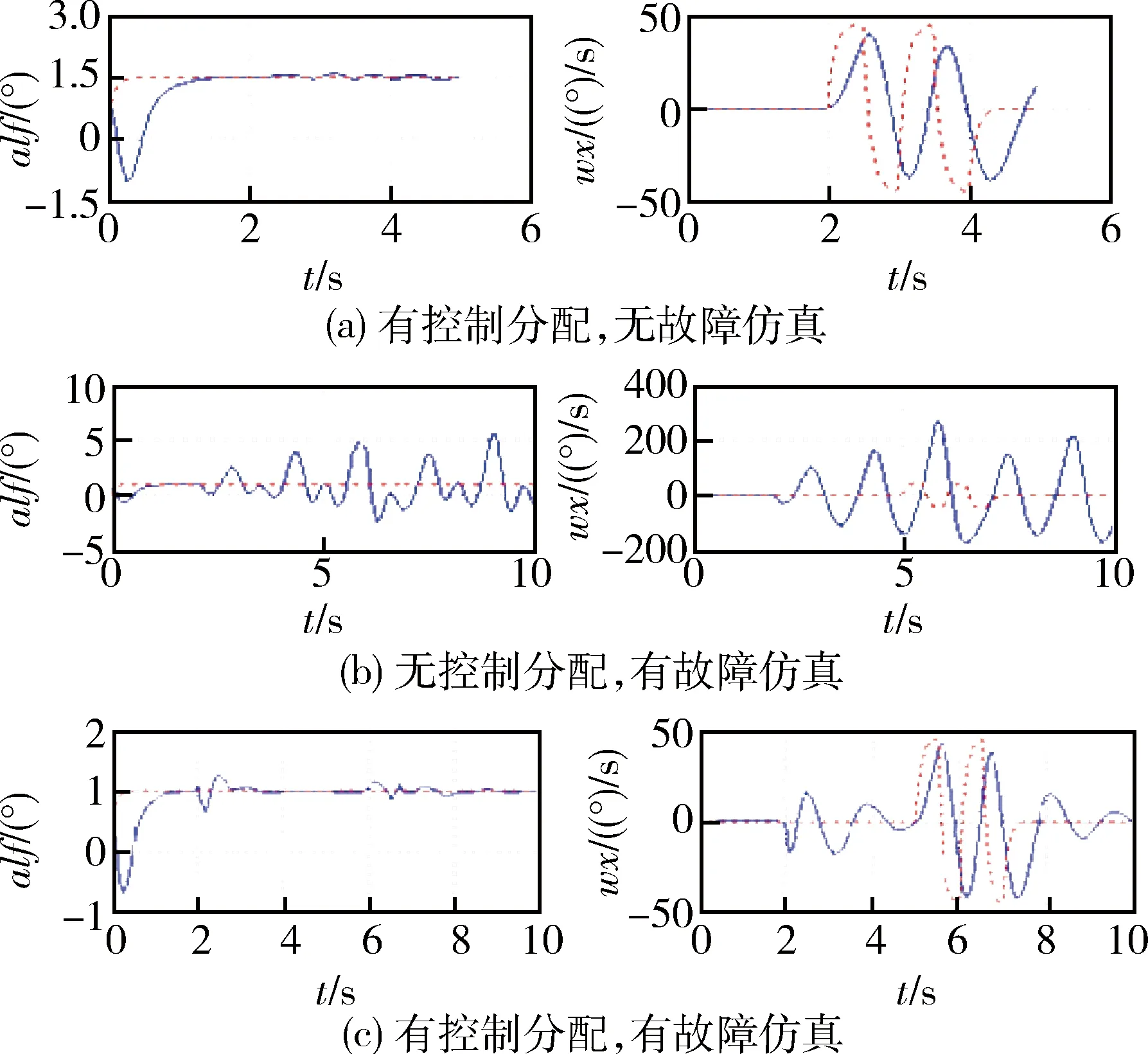
设控制变量u∈Ω⊂Rm,其中,控制空间Ω={u∈Rm|uiMin≤ui≤uiMax,i=1,2,…,m},其边界为∂Ω,位于边界上的控制量记为u*∈∂Ω。通过线性映射B:Rm→Rr,可以由u得到r维力矩矢量v,r 已知B,Ω和某一期望的vD,确定uD,使得BuD=vD的问题就是控制分配问题。若矩阵B行满秩,uD存在但不唯一,控制分配问题是可解的。 2.2 基于二次规划的动态最优控制分配法[10] 对于第i(i=1,2,…,m)个操纵面,考虑其偏转位置和速率限制,设 (1) 该系统为数字控制系统,存在合理的近似时间微分 (2) 式中T为采样时间。因此单采样周期内控制量满足 (3) 定义考虑控制力矩实现精度和速率限制惩罚项的二次型目标函数,将控制分配问题转化为受限条件下的二次规划问题: (4) 其中:W1,W2为用来控制力矩实现精度及控制舵面速率限幅的加权系数,us(t)期望的控制分配输入,一般通过对Bu(t)=v(t)求伪逆或加权伪逆得到。 该二次规划问题的最优解为: u(t)=Eus(t)+Fu(t-T)+Gu(t) (5) 其中: (6) 2.3 自适应加权阵算法 通常情况下,加权阵W1,W2都是依据操纵性能分析离线选取的。W1权值阵影响稳态控制量,权值的选择直接影响稳态下控制分配比例,应根据操纵面的操纵效率进行选择;W2则影响动态的分配过程,可根据操纵面的最大偏转速率进行合理选择。但是,飞行中如果出现操纵面故障(卡死或者悬浮),离线选择的权值阵就无法反映操纵面故障所引起的操纵效率的变化,从而会使控制优化分配的方向出现偏差。 为了提高二次规划动态控制分配方法对操纵面故障的鲁棒性,本文提出在线自适应加权阵计算方法,将最优控制理论中的“罚函数法”引入加权阵计算过程,根据操纵面的操纵效率变化,通过调节与之对应的罚值,在线调控各操纵面控制分配的寻优方向。 定义w1i,w2i为第i(i=1,2,…,m)个操纵面操纵效率相关的罚函数,计算方法如下: w1i=w1i,0+σ1i (7) 其中:w1i,0,w2i,0为权值初始值,σ1i,σ2i为罚值,则加权系数由各操纵面的罚函数构成 (8) 另外,定义参数pi(i=1,2,…,m)来表示第i个操纵面的舵机实际响应量与其控制指令的比值,作为反映该操纵面的实时操纵效率的指标参数。操纵面罚值的大小可根据参数pi来确定。当pi接近0时,表示舵面不能很好地响应控制指令,甚至有可能已经卡死,此时对该操纵面的惩罚应较大,体现在罚值上应取σ1i较小,σ2i较大,即控制量尽可能不分配给此舵面;反之,当pi接近1时,舵面能够很好地响应控制指令,对操纵面的惩罚应较小,取σ1i较大,σ2i较小。 由于惩罚程度、罚值与操纵面实时效率的关系较为复杂,引入模糊控制理论中的模糊集合以及隶属度函数概念,依据工程实践经验,制定由参数pi来实时调整罚值的模糊推理规则,用公式表示如下: (9) 图3~4给出了σ1i,σ2i随pi变化的曲线示意图。 图3 σ1i随pi的变化曲线 图4 σ2i随pi的变化曲线 以某面对称飞行器为对象,对本文所提出的自适应飞行控制律进行仿真验证。 表1 操纵面名称、符号及参数 在欧美系下建立飞行器模型,采用Matlab进行仿真验证;舵系统及故障的设置用Simulink搭建,包含速率限幅,延时等非线性环节。图5为动态逆+自适应控制分配原理框图。 图5 动态逆+自适应控制分配原理框图 选取三轴姿态指令分别为5°倾侧角、10°攻角和-3°侧滑角;操纵效能矩阵B和初始权值取值[13]分别为 (10) w1i,0=2,i=1,2,…,7 (11) w2k,0=10,k=3,…,7 三轴姿态控制仿真结果由图6~7给出。图6是姿态角和姿态角速度仿真曲线,图7是各操纵面偏转角曲线。三轴姿态角阶跃响应达到稳态的时间均小于1s,且无超调和稳态误差,各操纵面的偏转量和偏转速度均较小,能够满足要求。 图6 三轴姿态控制结果 图7 操纵面偏转曲线 为检验自适应控制律在操纵面故障情况下的效果,进行了控制分配器和故障情况组合条件下的对比仿真。故障情况为右外侧副翼卡死,自适应控制分配的权值曲线如图8所示,仿真条件和结果如图9所示。由仿真结果可知,在无控制分配器的情况下,一旦有故障,则飞行器不能很好地跟踪控制指令,最终导致发散。在控制分配器作用下飞行器依然能够跟踪控制指令,稳定飞行。 图8 故障操纵面控制分配权值曲线 图9 故障情况对比仿真结果(——响应曲线,┅ ┅指令曲线) 提出了一种基于自适应控制分配的飞行控制方法,飞行控制律采用动态逆方法设计,而自适应控制分配方法是在常规的二次规划动态控制分配方法中引入与操纵面作用效率相关的罚函数,提升了动态控制分配算法对操纵面故障的容错能力。 从仿真结果中可以得到以下几点结论: 1) 由于使用了动态逆控制律,在模型较为精确的情况下,能够提供较为理想的响应结果; 2) 自适应动态分配方法能使各操纵面的偏转较为均衡,没有出现较大的偏转量、偏转速度; 3) 故障情况的对比仿真显示,该控制方法能够提升控制器对伺服故障的鲁棒能力,在伺服故障下也能够实现期望的控制性能。 [1] 马建军,李文强,李鹏,郑志强.飞行器控制分配技术研究现状与展望[J].飞行力学, 2009,27(3): 1-5,10.(MA Jianjun, LI Wenqiang, LI Peng, et al. Status and Future of ControlAllocation for Aerospace Vehicle[J]. Flight Dynamics, 2009, 27(3): 1-5,10.) [2] Oppenheimer M , Doman D , Bolender M. ControlAllocation for Over-actuated Systems[C].Mediterranean Conference on Control and Automation, 2006: 1-6. [3] Buffington J M. Tailless Aircraft Control Allocation[R]. AIAA-97-4281, 1999. [4] ReigelspergerW C, Banda S S. Nonlinear Simulation of Amodi-fied F-16 with Full-envelope Control Laws[J]. Control Engineer Practice, 1998, (6): 309-320. [5] Durham W C.Constrained Controlallocation[J]. Journal of Guidance, Control and Dynamics, 1993, 16(4): 717-725. [6] Kevin R S, Durham W C. A Comparison of Control Allocationmethods for the F-15 Active Research Aircraftutilizing Real Timepiloted Simulations[R].AIAA-99-4281, 1999. [7] Yu Liu, Luis G Crespo.Adaptive Control Allocation in the Presence of Actuator Failures[J]. AIAA Paper 2010-7772. [8] Oppenheimer Michael, Doman David, Bolender Michael,Michael W.Application of Piecewise Linear Control Allocation to Reusable Launch Vehicle Guidance and Control[R].ADA454301, 2006. [9] 臧希恒,唐硕. 基于线性矩阵不等式的动态控制分配方法研究[J]. 航天控制,2013,31(2):16-22.(ZANG Xiheng, TANG Shuo. Dynamic Control Allocation Based on Linear Matrix Inequality[J].Aerospace Control, 2013, 31(2): 16-22.) [10] 占正勇,刘林.多操纵面先进布局飞机控制分配技术研究[J].飞行力学,2006,24(1):13-16,21.(ZHAN Zhengyong, LIU Lin. Control Allocation for High Performance Aircraftwith Multi-Control Effectors[J]. Flightdynamics, 2006,24(1):13-16,21.) [11] James M Buffington,Andrew G Sparks. Comparison of Dynamic Inversion and LPV Tailless Flight Control Law Designs[C].Proceedings of the American Control Conference Philadelphia, Pennsylvania June 1998. [12] Ola Härkegård. Dynamic Control Allocation Using Constrained Quadratic Programming[C].AIAA Guidance Navigation, and Control Conference and Exhibit, Monterey, CA, Aug. 2002. [13] 柳扬,安锦文.多操纵面战斗机动态控制分配策略研究[J].计算机仿真,2008,25(5):33-36. [LIU Yang,AN Jinwen. Dynamic Control Allocation of Fighter with Multi-effectors[J]. Computer Simulation,2008,25(5):33-36.) A Fault-Tolerant Flight Control Method Based on Adaptive Control Allocation Algorithm ZHANG Zhiyao HUANG Wanwei LIU Jiarun Beijing Aerospace Automatic Control Institute, Beijing 100854, China Aimingatensuringsafetyandimprovingflightperformanceofflightvehiclewithmultiplecontrolsurfaces,anewflightcontrolmethodbasedonadaptivecontrolallocationalgorithmisproposed.Firstly,thenon-lineardynamicinverseflightcontrolmethodisintroduced.Secondly,theadaptivedynamiccontrolallocationisobtainedbyintroducingfuzzypenaltyfunctionrelatedtocontrolsurfacesefficiencyintonormalconstrainedquadraticprogramming.Finally,thesimulationresultswithservofailuresandwithoutservofailuresshowthevalidityandsuperiorityoftheproposedmethod. Adaptivecontrol;Controlallocation;Multiplecontrolsurfaces;Dynamicinverse;Quadraticprogramming 2013-11-13 张之瑶(1989-),女,西安人,硕士研究生,主要研究方向为导航、制导与控制;黄万伟(1970-),男,湖南醴陵人,博士,研究员,主要研究方向为飞行器姿态控制、变结构控制、智能控制理论与应用等;柳嘉润(1979-),男,长沙人,高级工程师,主要研究方向为导航、制导与控制。 V249.1 A 1006-3242(2014)03-0023-06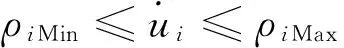
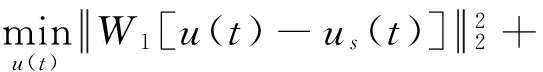

w2i=w2i,0+σ2i
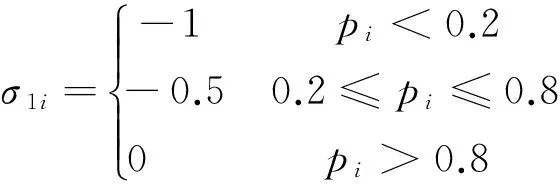
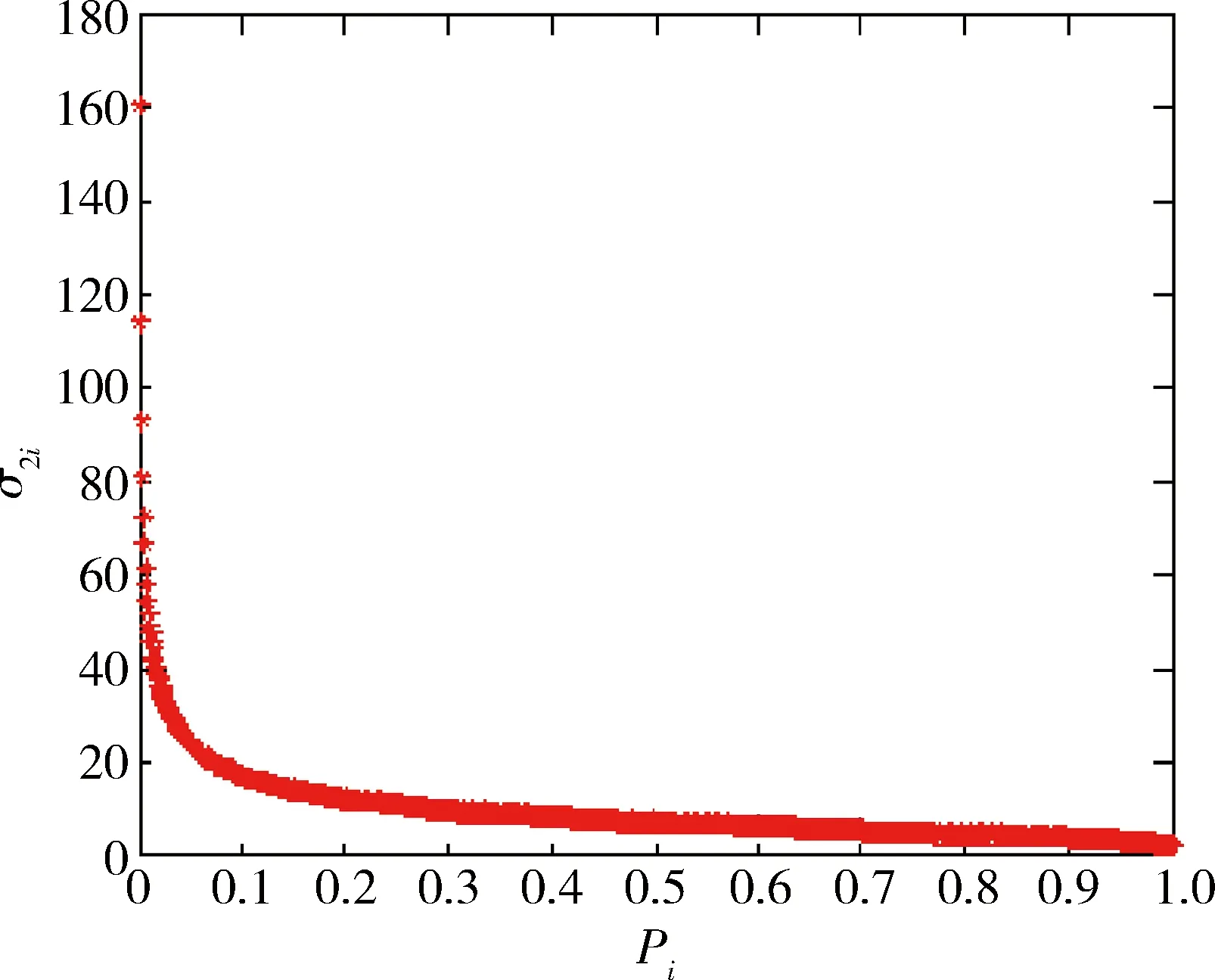
3 仿真验证



w2j,0=5,j=1,2

4 结论

