卫星混合执行机构的可重构性研究*

胡宇桑 王大轶 刘成瑞

1. 北京控制工程研究所, 北京 100190 2. 空间智能控制技术重点实验室, 北京 100190



卫星混合执行机构的可重构性研究*

胡宇桑1,2王大轶1,2刘成瑞1,2

1. 北京控制工程研究所, 北京 100190 2. 空间智能控制技术重点实验室, 北京 100190

针对含混合执行机构的姿态控制系统中常见构型配置问题进行研究，选择金字塔(PC)、五棱锥安装(FPC)的单框架控制力矩陀螺群(SGCMG)与三正一斜装、四斜装的动量轮(MW)分别进行执行机构组合构型比较。根据提出的构型评价指标，考虑各组合构型因故障进行重构情形，从角动量包络、执行机构功耗、系统控制性能、构型安装位置等方面研究卫星混合执行机构的可重构性。通过对各混合构型及其重构构型完成姿态大角度机动进行仿真，得到相关可重构性研究结论，结果表明混合执行机构的可重构性与构型安装数目及位置有着密切的关系，执行机构功耗也影响其可重构能力等，可以为卫星混合执行机构可重构性评价和设计提供相关参考。

混合执行机构；构型配置；可重构性；姿态机动

随着卫星任务需求呈现多样化趋势，使用混合执行机构成为研究热点。星上常用执行机构有：动量轮、推力器和控制力矩陀螺。与推力器相比，动量轮和控制力矩陀螺能产生精确且连续的力矩，且具有无污染、节省燃料、显著延长卫星在轨寿命等优点；动量轮提供力矩小不适于快速机动，常用于高精度三轴对地稳定控制；控制力矩陀螺在同等重量下能提供较动量轮更大的控制力矩，但有结构复杂，易发生奇异等问题。采用SGCMG和MW组成混合执行机构，可发挥各自优势，实现航天器的高性能姿态控制。文献[1]提出采用金字塔构型和3个MWs共同进行太空望远镜姿态稳定控制方案；文献[2]提出在卫星姿态机动控制中用SGCMGs进行姿态粗控，MWs进行姿态精确调整的方案；文献[3]在航天器能量姿态一体化控制中，也提出利用SGCMGs与MWs来完成。目前混合执行机构控制分配方面的研究较多，关于混合执行机构构型选取及失效后重构性能研究较少。

文中将对几种常用混合执行机构组合进行分析，SGCMG群选用金字塔、五棱锥构型，MW选用三正一斜装(3+1t)、四斜装(4t)构型，通过对各组合构型的角动量包络、功耗、控制性能、安装位置等比较，得出关于混合执行机构可重构性相关结论，为卫星姿态控制系统可重构性评估及设计提供参考依据。

1 混合执行机构建模及常用构型

图1为本文采用的混合执行机构姿态控制系统框图。建模得到卫星本体系下的姿态动力学方程为：

图1 卫星混合执行机构姿态控制系统方框图

(1)

(2)

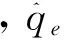
(3)

(4)

图2 混合执行机构安装构型示意图

因构型具有对称性，金字塔构型任意失效均为同一种失效形式。五棱锥在失效1个时为2种形式(加轴陀螺S1失效和S2-6中任意一个失效)，FPC失效2个含有3种形式：S1234(234陀螺相邻)，S1235(235陀螺相间)，S2345(加轴S1陀螺失效)，FPC失效3个为4种形式：S123，S124，S234，S235。动量轮采用3+1t及4t构型，3+1t失效1个后为2种形式：2+1t和3正交；4t任意轮失效后均为3t形式。

2 混合执行机构可重构性研究

2.1 基于角动量包络的可重构性研究

采用常见的SGCMG群角动量包络评价指标：构型效益和失效效益[7]，绘制各构型及其重构构型的奇异角动量包络[8]来进行指标对比。

1) 构型效益：某构型的构型效益为SGCMG系统的动量包络上的最小角动量与陀螺群角动量的代数和之比。

(5)

式中，ξ为由动量体中心指向包络的方向，n为SGCMG的个数，h为单个陀螺的标称角动量。构型效益越大，说明单个SGCMG发挥的效益越大。

2) 失效效益：某构型的失效效益为SGCMG系统失效一个单框架控制力矩陀螺后的动量包络上的最小角动量与失效前陀螺群角动量的代数和之比。

(6)

表1中不考虑失效，五棱锥各项指标全面占优，具有较大的角动量包络，且凹陷浅、冗余度高。FPC和PC构型重构后的构型效益、失效效益均明显下降， FPC失效2个比失效1个各指标下降更多，说明多次重构构型的角动量包络变形严重。对比4-SGCMG构型，金字塔各指标较高。因此，SGCMG群重构应尽量选择角动量包络对称性好、体积大的构型。

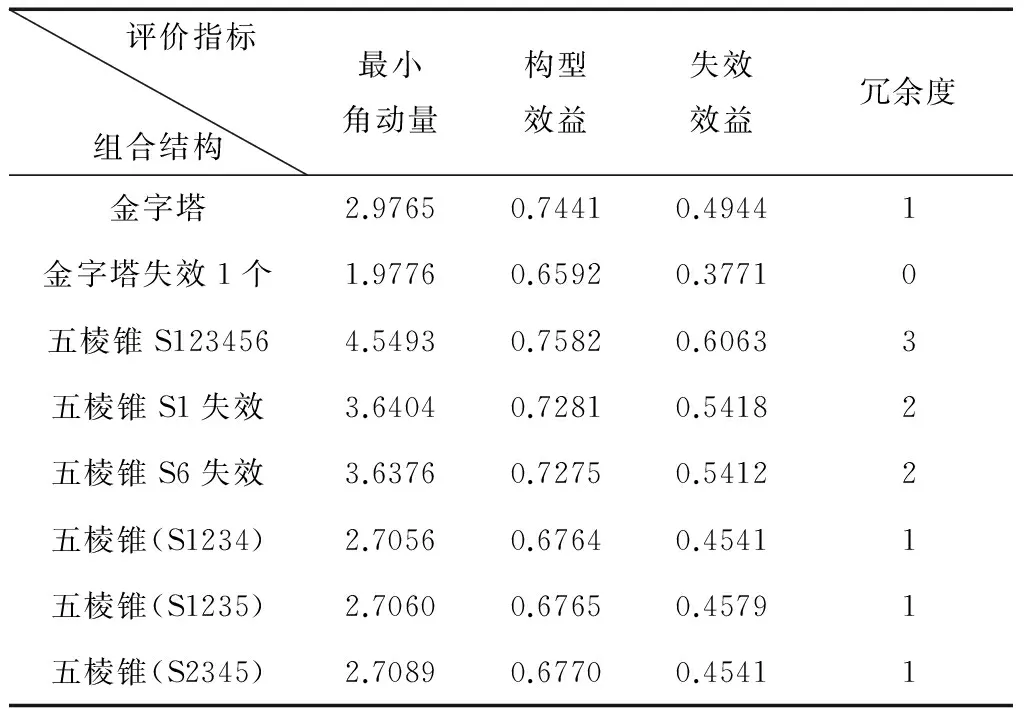
表1 SGCMG典型构型评价指标对比

动量轮角动量包络的体积与储存角动量能力有关。为更好地比较动量轮装置对卫星三轴具有的控制作用，选用动量指标γm来衡量动量轮角动量包络[9]：

γm=(Hx+Hy+Hz)/nHw

(7)

式中，Hx，Hy，Hz分别为滚动、俯仰、偏航轴产生的最大角动量，n为动量轮个数，Hw为每轮最大角动量。

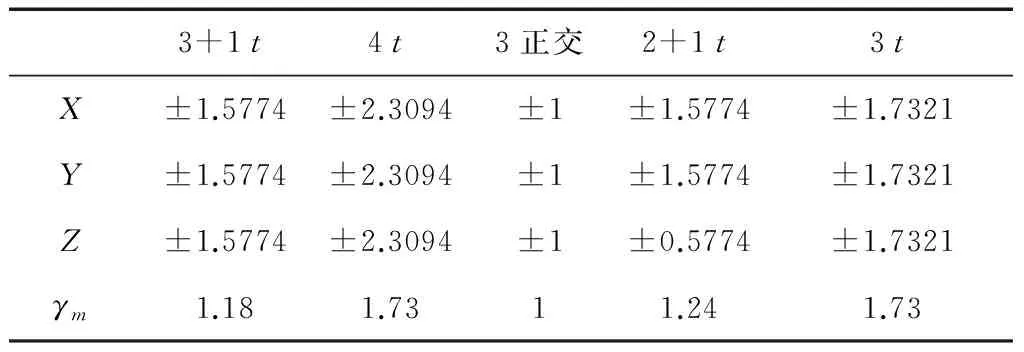
表2 动量轮三轴最大角动量及构型动量指标比较

表2中 4t和3t的三轴最大角动量值最高，三正交和2+1t的最大角动量值较低，且2+1t的三轴最大角动量值不均衡。四斜装和三斜装的动量指标值最高，构型的三轴角动量存储能力更强，需要同等大小的角动量时，动量轮卸载次数减少。四斜装的角动量包更大，在存储外扰角动量能力将显示出更大的优势[10]，且在重构时的动量指标高于三正交一斜装。

综上，FPC与四斜装动量轮组合的角动量包络最优，金字塔与三正一斜动量轮组合角动量包络构型较差；考虑重构构型中，FPC失效2个时与动量轮失效1个时的2+1t组合构型的角动量包络各项指标较低，应避免选取该组合类型。

2.2 混合执行机构功耗与可重构性能研究

(8)

表3 SGCMG功耗指标

仿真各构型分别与四斜装动量轮组合进行姿态机动的功耗指标，设置初始框架角组合接近奇异状态。表3中数目多的SGCMG群功耗指标较低，数目少的功耗指标较高；当陀螺群拥有相同数目时，功耗指标相差小。

(9)

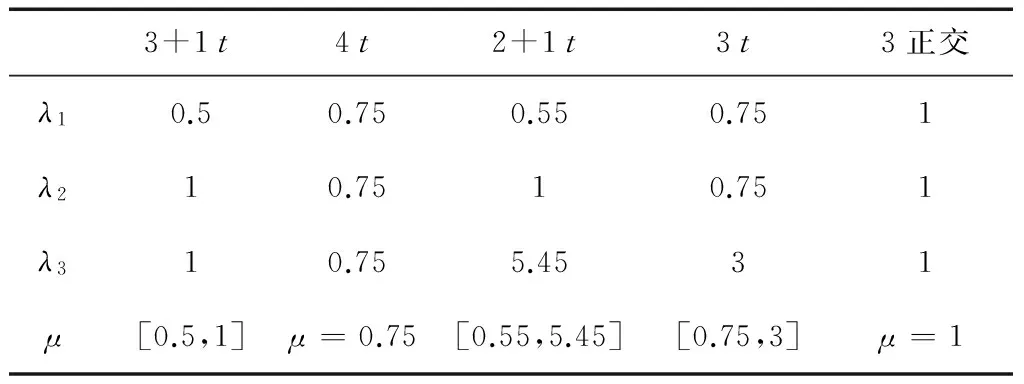
表4 动量轮功耗指标

从表4可以看出，四轮构型各主轴通道功耗指标均小于1，且四斜装构型三轴功耗均是三正交轮的3/4。考虑失效重构时，二正一斜装、三斜装的功耗指标最大值增为5.45和3，说明2+1t和3t较三正装功耗分配不均衡，当所需力矩方向分布均匀时，重构构型的总功耗均比三正交构型消耗增多。

由功耗分析发现，该混合执行机构在故障重构时，SGCMG群和动量轮的功耗均增加，且重构构型变化将引起功耗消耗有差异；当重构所需功耗过大不能满足真实系统能量约束条件，实际上也无法实现重构。因此，根据姿态控制任务需求来选择合适的构型，减小功耗消耗，增强可重构能力。

2.3 混合执行机构控制效果与可重构性研究

采用SGCMG与MW混合执行机构能有效利用动量轮使SGCMG远离奇异状态，但传统度量奇异指标D的最大值与构型数目有关，故定义远离奇异率来更好地度量远离奇异状态程度。

远离奇异率：逃离奇异后，SGCMG群的奇异度量达到的稳态值与该构型奇异度量最大值之比。

τ=Dfinal/Dmax=Dfinal/(n3/27)

(10)

表5 各构型远离奇异率比较

仿真各组合构型姿态机动得到τ如表5所示。各SGCMG构型与四斜装动量轮组合后均比与三正一斜组合的远离奇异率高；五棱锥含陀螺越多的构型τ更高，说明数目多的陀螺群陷入奇异机率降低；分析4-SGCMG+4-MW组合构型情况，金字塔构型的远离奇异率最高，五棱锥不含加轴陀螺时远离奇异率最低。远离奇异率与SGCMG群重构的数目和动量轮采用构型有着密切的关系。

混合执行机构还需考虑动量轮转速易饱和问题，发现输出相同期望力矩时， 4t,3+1t构型比3t,2+1t、3正交构型的轮子转速饱和速度慢，因而达到转速饱和状态少，在含3个轮子的动量轮构型中，三正交构型轮子转速增量均衡，与奇异点分布均匀的陀螺群混合仍有较好奇异逃离能力。仿真组合构型显示4-SGCMG +4-MW姿态控制性能较好，3-SGCMG+ 3-MW的控制力矩陀螺群逃离奇异时间较长、构型奇异点增多，框架转轴的角速度更大，需要提供的能耗增量最多，说明在多次失效进行多重重构时，系统性能上会受到一定的影响，需要对控制律进行重构或者其它重构方式来达到相关系统性能要求。

2.4 构型位置与可重构能力

考虑混合执行机构角动量包络、功耗、奇异情况、及动量轮转子转速增幅等，汇总得到结论如下表。

表6 各混合执行机构组合方案比较

表6表明，SGCMG群加轴位置有陀螺，如五棱锥构型，加轴位置陀螺对陀螺群的控制性能有很大的影响。数目较多、冗余性强的控制力矩陀螺构型在2个或2个以上失效时，剩余陀螺含有相间位置(如S125)均比相邻位置(S123)的构型角动量包络对称性好，构型的可重构能力更优。

2.5 可重构性评价及设计参考准则

通过对常用混合执行机构构型比较，为其可重构性评价及设计提供思路：

1) 构型选取：尽量选角动量包络大且对称性强的构型，如FPC构型、动量轮4t构型。从SGCMG群规避奇异能力来看，需4个MW时应选择四斜装构型，需3个MW时三正交构型更好。

2) 数目选取：数目多的构型可重构性较高，满足可靠性后，适当选择数目较少构型。混合执行机构中，选用奇异点较少的SGCMG构型，则动量轮可用较少数目。完成单次机动时，数目多的SGCMG群消耗功耗低，适宜频繁机动。

3) 重构位置选取：FPC各位置失效影响略有差别，5-SGCMG构型的加轴位置失效后重构性能没有非加轴位置失效后重构性能好；4-SGCMG构型的含有加轴位置陀螺构型较优；3-SGCMG构型的重构性能较差，尽量选择陀螺相间构型。

4) 综合可重构能力：FPC构型有多次可重构能力，适于长期在轨使用；PC构型重量占优，与四斜装动量轮混合可重构能力强，适于机动性强的中小型卫星。

3 仿真分析

仿真根据lyapunov方法设计姿态控制律，用奇异值分解的方法对指令力矩进行显示分配，选用文献[4]中的方法设计控制力矩分配操纵律，取η=0.3,k(D,0.3)=100(D-0.3)2。卫星主轴转动惯量Ix,Iy,Iz分别为,723.6 Kg·m2,1259 Kg·m2,1136.7 Kg·m2,卫星三轴初始姿态角0°，期望姿态角30°；SGCMG提供最大输出力矩10Nm，框架角最大转速0.5rad/s，动量轮输出最大力矩0.4Nm，外界干扰为10-4Nm量级的周期性力矩。仿真五棱锥、金字塔、五棱锥(S1234)、五棱锥(S2345)与四斜装动量轮组合，得到的曲线如下所示。

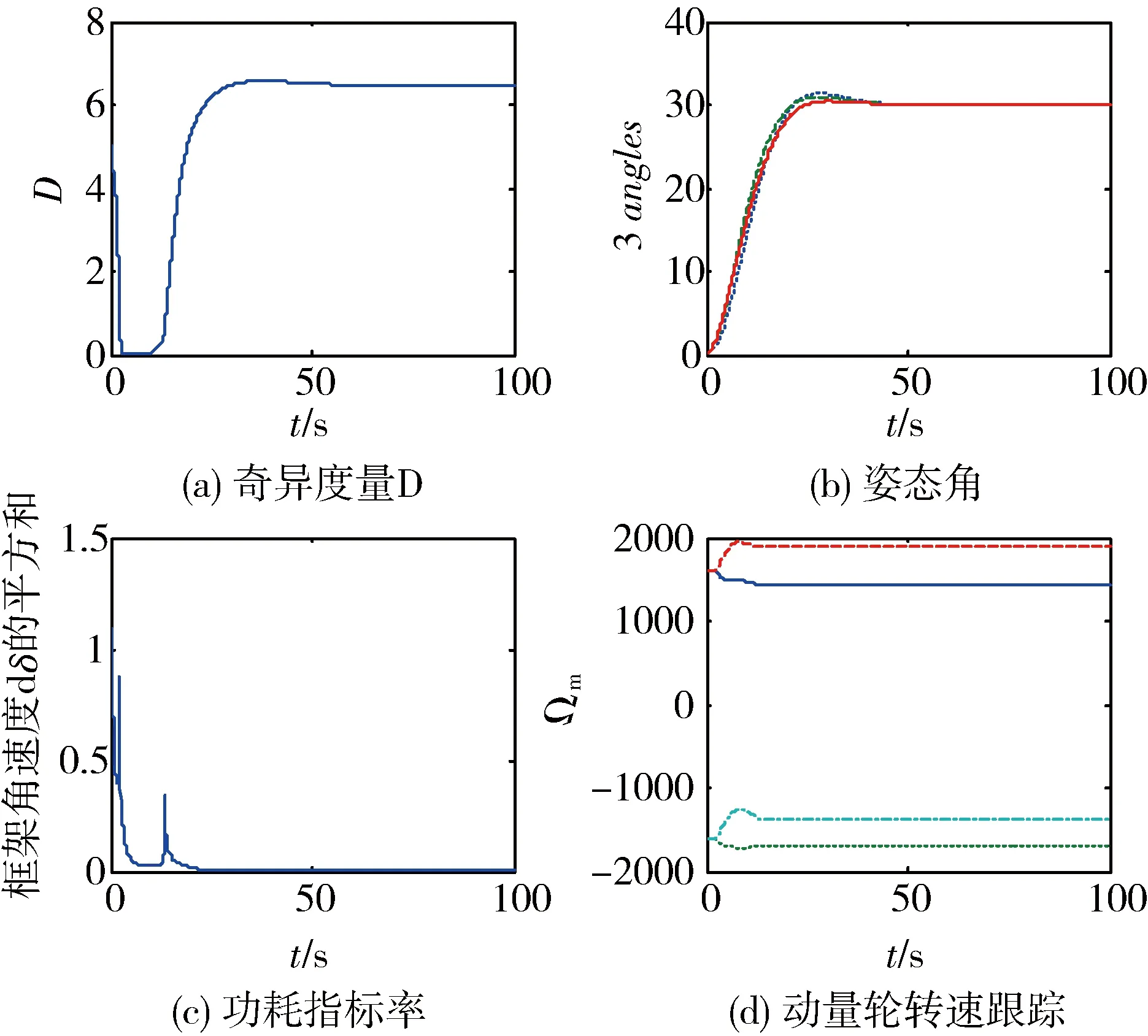
图3 五棱锥SGCMG群+动量轮四斜装仿真图

图4 金字塔SGCMG群+动量轮四斜装仿真图

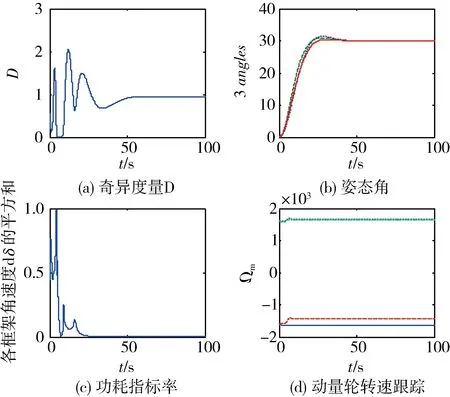
图5 五棱锥SGCMG群(S1234)+动量轮四斜装

图6 五棱锥SGCMG群(S2345)+动量轮四斜装

图7 动量轮各重构构型仿真对比

图7为金字塔SGCMG构型与动量轮失效1个后的重构构型组合的仿真曲线比较，发现奇异度量值均比动量轮未失效时明显下降，陀螺群规避一次奇异后的远离奇异率低。比较3种动量轮失效构型的动量轮转速跟踪曲线，发现动量轮转速增量从低到高排列为：三正交、三斜装和二正一斜装，与前文动量轮重构构型功耗分析相符。

4 总结

本文研究含SGCMG群和动量轮的混合执行机构姿控系统的可重构性，从角动量包络、功耗、控制能力、构型位置等方面分析常用构型，得到结论如下：

1) 所研究的混合执行机构在2类机构各含有大于3个数目时均具有可重构能力，且冗余度越高，重构构型可选方案越多；

2) 混合执行机构各类数目均相同的构型中，角动量包络对称性强、分布均匀、包络大的构型具有较好的重构能力；

3) 失效破坏构型的对称性，无论是控制力矩陀螺还是动量轮，由不同位置失效后的重构构型在奇异规避、能量消耗、控制性能方面均存在差异；

4) FPC构型具有多重重构能力，适合长期在轨运行卫星；金字塔构型与四斜装动量轮为机动性要求强的卫星的最佳混合构型。

[1] RYBAK, S C; LIEBERMAN, S I.Achieving Ultrahigh Accuracy with a Body Pointing CMG/RW Control System[C]. Guidance and Control Conference, United States, AIAA,20-22 Aug. 1973, 12.

[2] Skelton C E , Christopher D H. Mixed Control Moment Gyro and Momentum Wheel Attitude Control [C] . AAS03-558 ,2003.

[3] Christopher D K. Robust Reorientation and Power Controller Using Flywheels and Control Moment Gyroscopes[J ] . Journal of Guidance Control and Dynamics ,2006 ,29 (1): 217-220.

[4] 金磊,徐世杰.采用单框架控制力矩陀螺和动量轮的航天器姿态跟踪控制研究[J].宇航学报,2008,29(3): 916-921.(Jin lei,Xu Shijie.Attitude Tracking Control of a Spacecraft Using Single Gimbal Moment Gyros and Momentum Wheels[J].Journal of Astronautics,2008,29(3): 916-921.)

[5] 周黎妮,李海阳,唐国金.空间站基于动量管理的集成能量与姿态控制系统[J].宇航学报,2009,30(6):2151-2158.(Zhou Lini, Li Haiyang, Tang Guojin. Momentum-Management-Based Integrated Power and Attitude Control System for Space Station[J] .Journal of Astronautics, 2009,30(6): 2151-2158.)

[6] 耿云海,侯志立.使用混合执行机构的快速机动卫星力矩分配算法[J].宇航学报,2013,34(5): 611-616.(Geng Yunhai,Hou Zhili.Hybride Actuator Control Torque Allocation Algorithm for Rapid Maneuver Satellite[J].Journal of Astronautics, 2013,34(5)： 611-616.)

[7] 张锦江.单框架控制力矩陀螺系统的构型分析和对比研究[J].中国空间科学技术, 2003，(6): 52-56.(ZHANG J J. Research on Configuration Analysis of Singlegimbal Comparison of SGCMG System[J].Chinese Space Science and Technology, 2003，(6):52-56.)

[8] 汤亮.使用控制力矩陀螺的航天器姿态动力学与控制问题研究[D].北京：北京航空航天大学，2005.(TANG L.A Research on Attitude Dynamics and Control of Spacecraft with Control Moment Gyros[D].Beijing:Beijing University of Aeronautics and Astronautics,2005.)

[9] 林来兴,白拜尔.卫星姿态控制反作用轮的最佳安装结构[J].自动化学报, 1984,10(3):228-238.(Lin Laixing, Bai Baier. Optimal Mounting Configuration of Reaction Wheels for Satellite Attitude Control[J]. Acta Automatical Sinica, 1984,10 (3):228-238.)

[10] 章仁为.卫星轨道姿态动力学与控制[M].北京：北京航空航天大学出版社，1998.(ZHANG Renwei. Orbital Attitude Dynamics and Control of Satellite [M]. Beijing: Beijing University of Aeronautics and Astronautics,1998.)

Reconfigurability Research on Satellite Control System with Mixed Actuators

HU Yusang1,2WANG Dayi1LIU Chengrui1,2

1. Beijing Institute of Control Engineering, Beijing 100190, China 2. Science and Technology on Space Intelligent Control Laboratory, Beijing 100190, China

Theconfigurationselectionofthemixedactuatorsinsatelliteattitudecontrolsystemdesignwasinvestigatedinthispaper.Choosepyramidconfiguration(PC),fivepyramidconfiguration(FPC)ofsinglegimbalcontrolmomentgyroscopes(SGCMGs)andthreeorthogonalwithoneskewedmomentumwheels,fourskewedmomentumwheelstocombineandanalysis.Accordingtosomeproposedconfigurationindices,theangularmomentumenvelope,energyconsumption,theperformanceofcontrolsystemandtheinstallationpositionweretakenintoaccountinthereconfigurabilityresearch.Differentmixedconfigurationsandtheirreconstructedconfigurationswerecomparedbysimulation,theresultsrevealedthatthenumberofSGCMGsandRWsandtheinstallationpositionhadacloserelationwithreconfigurability,powerconsumptionofactuatorsalsoaffectedtheirreconfigurability.Theresultscanprovideseveralsuggestionsforthereconfigurabilityevaluationanddesignofthemixedactuatorssystem.

Mixedactuators;Configuration;Reconfigurability;Attitudemaneuver

*国家自然科学基金资助项目(61203093,61004073)

2013-03-12

胡宇桑(1989-)，女，湖南人，硕士研究生，主要研究方向为航天器导航、制导与控制；王大轶(1973-)，男，黑龙江人，研究员，主要研究方向为航天器导航、制导与控制；刘成瑞(1978-)，男，河北人，高级工程师，主要研究方向为航天器故障诊断与可靠性研究。

V448.2

A

1006-3242(2014)03-0044-07