基于连续小波变换的Hilbert包络线松动部件定位方法

季田田，方力先，曾 复，张 卫，谢永诚，王赤虎，张可丰

(1.杭州电子科技大学，浙江 杭州 310018； 2.上海核工程研究设计院，上海 200233)

在核电站运行过程中，松脱部件的出现即意味着核电站安全性能的减弱，甚至会给核电站造成重大安全事故。松动部件监测系统(LPMS)作为核电站一回路重要的检测系统之一，为核电站的安全、稳定运行提供了重要保障。松动部件定位作为LPMS的关键技术之一，准确地实现松动部件定位有利于为核电站运行人员判断是否停堆检修提供依据，有利于在停堆检修时快速找到松动部件，尽量减少维修人员暴露在核辐射下的时间。核电站松动部件定位的方法可分为：到达时差(TDOA)定位法、圆相交定位法和扫描定位法。其中圆相交定位法应用成熟度不高，扫描定位法耗时太长，相比之下，到达时差定位法应用最为广泛，计算速度也较快。到达时差定位法主要是根据碰撞信号的波速和信号到达各传感器的时间差这两个参数实现松动部件定位。在到达时差估算方法中，时域累积法、时域均方根法、信号相关法[1-2]的抗噪声干扰能力较差，基于小波去噪的时差估计方法[3-4]虽提高了抗噪能力，但该方法是以信号的过零点作为信号到达时刻，未考虑弯曲波的复杂传播模式，所以在实际定位中，当传播距离较远时仍存在较大的定位误差。基于Hilbert变换的到达时差估算方法[5]以Hilbert包络线的第1个峰值作为信号到达点，并通过计算信号的主频率来计算弯曲波的群速度，该方法虽具有较好的抗噪能力，但由于未考虑弯曲波复杂的频率成分及波的频散效应，仅以信号主频率来计算弯曲波群速度，所以当传播距离较远时仍存在较大定位误差，且在实际情况下，计算弯曲波速度的一些相关参数也较难获得。

本文结合时-频域信号处理方法，提出基于连续小波变换(CWT)的Hilbert包络线松动部件定位方法(CWT-Hilbert包络线法)，该方法综合小波时-频域局部化分析和Hilbert包络线主频能量突显的特点，通过提取冲击信号主频带内信号Hilbert包络线的峰值来确定信号的到达时刻。

1 连续小波变换

CWT的表达式[6]为：

(1)

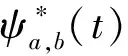
由式(1)可知，CWT是时-频域局部化分析，它通过伸缩、平移运算对信号逐步进行多尺度细化，最终达到在高频处对时间进行细化，在低频处对频率进行细化，能自动适应时-频域信号分析的要求，从而可聚焦到信号的任意细节。

数字角频率与模拟角频率的关系为：

(2)

式中：Ts为采样周期；ω为数字角频率，以2π为周期；Ω为模拟角频率；f为模拟频率；fs为信号的采样频率。

设ψ(t)的频域中心为ω0，则ψa,b(t)的中心数字角频率ωa,b=ω0/a，根据式(2)，可得到数字中心频率ωa,b=Ωa,bTs，则小波变换时尺度因子和频率之间的关系[7]为：

Fa=FcTs/a

(3)

式中：Fc为给定小波的中心频率，为归一化后的数值；Fa为伪频率。

Fc与具体的小波有关，如对于dB2小波，Fc=0.666 7。由式(3)可看出，a与Fa的关系依赖于小波基函数和Ts。所以，可根据冲击信号主频率fm来确定尺度因子，而fm可根据冲击信号幅频特性确定。这样即可对经尺度因子连续小波变换后的信号实现特定时-频域内信号的突显，使信号所包含的能量主频带变窄，且CWT是等能量变换，从而减小了波的频散效应对波速的影响。图1为100 g钢球冲击信号在尺度因子为2时经CWT前、后的幅频图，图2为1.4 kg钢球冲击信号在尺度因子为20时经CWT前、后的幅频图。可看出，冲击信号经CWT前、后信号的主频带是一致的，且经变换后实现了主频带内信号的细化突显，使能量更集中。

2 Hilbert包络线

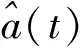
(4)

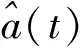
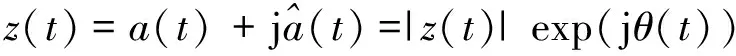
(5)

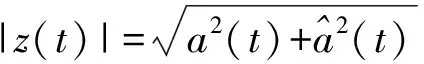
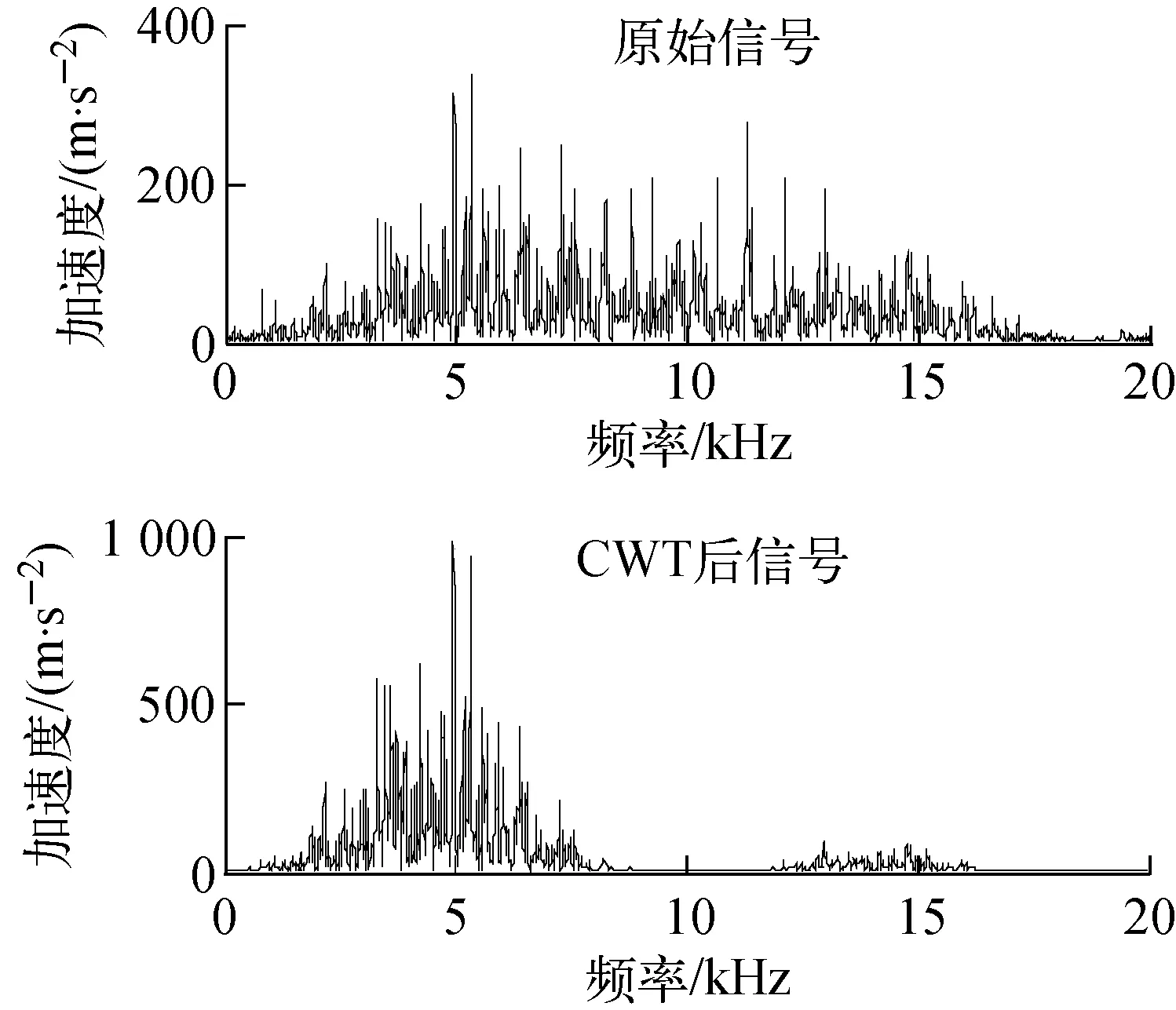
图1 100 g钢球冲击信号幅频图

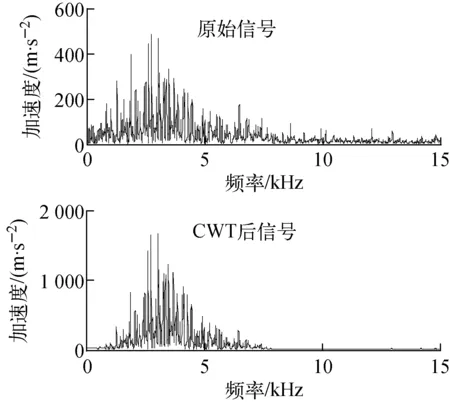
图2 1.4 kg钢球冲击信号幅频图

|z(t)|即为信号a(t)的包络线函数，反映了信号能量和时间的关系。鉴于传统方法较难有效识别信号的过零点，从而无法准确获得信号的到达时间，该方法通过提取信号的Hilbert包络线，认为Hilbert包络线的首个峰值所对应的时间即为冲击信号到达测量点的时刻。当松动部件和反应堆的压力容器发生碰撞时，碰撞能量主要以弯曲波的形式进行传播，其传播速度取决于弯曲波的群速度[9]。假设一弯曲波由n个频率很接近的简谐波组成，且其角频率分别为ω1、ω2、…、ωn，主频率为ωm(即各频率分量均接近于ωm)，则合成波a(t,x)可表示为：

(6)

式中：x为碰撞点与传感器之间的距离；ki为波数；bi为振幅。

根据合成波可构建新函数：

(7)

则信号的包络线函数可表示为：

(8)

根据波传播理论，弯曲波群速度cg与信号的波数和角频率的关系式为：

(9)

由于各角频率很接近，所以可得：

(10)

因此包络线上取得最大值时的时间点t可表示为：

(11)

由式(11)可知，冲击信号包络线的极值点所对应的时间点即为碰撞产生的弯曲波以速度cg传播距离x到达传感器的时刻。

由波传播理论可知，在被碰撞物材料和厚度已知的前提下，波的传播速度仅与频率有关，频率成分越单一，波速计算越精确，冲击信号经CWT后细化了主频带内的信号，在保证冲击信号能量不变的前提下使波的频率成分变得集中，从而减小了波速的估算误差对定位的影响。且Hilbert包络线法采用的是能量最大的弯曲波成分的速度，而经CWT后的信号恰好满足该条件，所以该方法对冲击信号起振点的确定较准确。、

3 实验与数据分析

3.1 实验平台与定位实现

因为核电站内松动件的冲击信号主要是以弯曲波的形式沿容器壁传播，核电站中传感器安装在容器壁上用来采集信号，所以对松动部件定位理论的研究性实验均通过平板冲击实验来实现，即用钢板来模拟容器壁，钢球来模拟松动件。平板冲击实验的实验平台由测试对象、传感器、电荷放大器、数据采集卡和计算机等构成，测试对象为钢板和卧式锅炉。钢板尺寸为200 cm×150 cm×2 cm，在钢板的4个边沿均加有缓冲隔离。冲击对象为钢球和力锤，钢球质量为20 g～11.2 kg，共16个，冲击高度分别为15、20、25 cm。背景噪声采集于大型卧式锅炉运行过程中的信号，其信号的频率结构与实际反应堆运行过程中信号的频率结构相近。

图3 网格划分

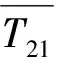
(12)

式中：i为网格编号；n为网格划分总数。

由式(12)计算得到的d(i)(1≤i≤n)可组成一n×1的数组dn×1，数组dn×1中的最小值所对应的i即为定位网格。

3.2 无噪声冲击实验分析

实验分析中矢量误差ve定义为：

ve=(x,y)

(13)

式中，x、y分别为松动件跌落位置所在网格与定位位置所在网格之间的水平间隔网格数和垂直间隔网格数。

相对误差Er定义为：

(14)

式中：|ve|为矢量误差的模；mh为网格的面积；s为以3个传感器为顶点构成的三角型的面积。

根据本文提出的定位方法，对不同质量冲击信号进行定位分析，其定位结果列于表1、2。从表1、2可看出，小质量冲击信号的定位平均相对误差较大，且随冲击质量的增大，定位平均相对误差逐渐减小，这与实际情况相符，即冲击质量越大越易实现定位。从定位结果看，所有钢球跌落位置的定位平均相对误差最小为2.60%，最大为13.12%。根据矢量误差可看出，定位网格与松动部件实际跌落网格的间隔约为1个网格，说明该方法对不同质量松动件均有较好的定位效果，其中大质量的松动件定位效果最好，且在实际应用中可通过减小网格划分尺寸来进一步提高定位精度。

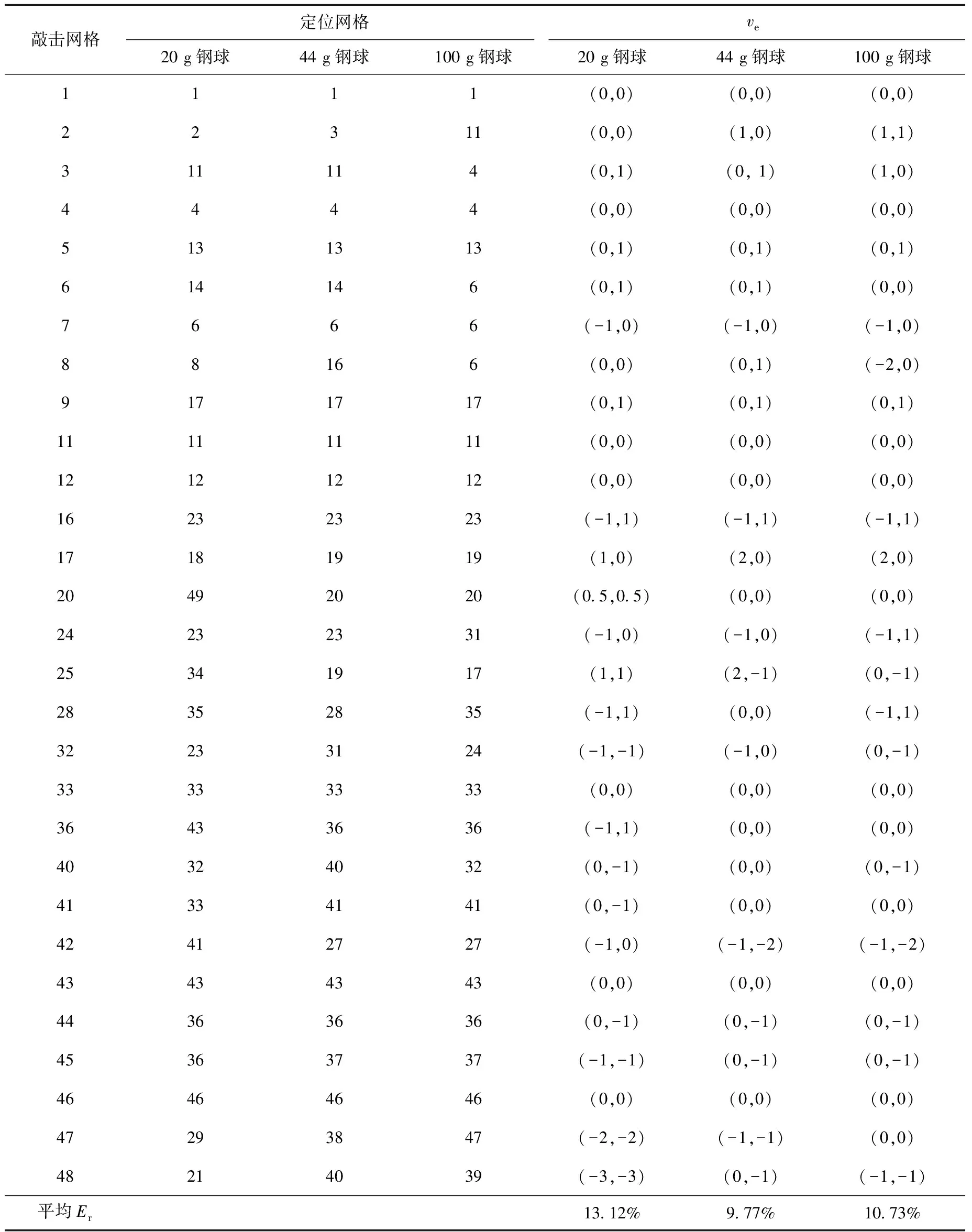
表1 小波尺度2下的定位结果

表3为CWT-Hilbert包络线法与Hilbert包络线法对175 g钢球冲击信号的定位分析结果。从表3可看出，CWT-Hilbert包络线法与Hilbert包络线法相比，在定位精度上有了很大提高，其定位平均相对误差为3.48%，而Hilbert包络线法的定位平均相对误差为15.16%。因此，本文提出的新方法在定位精度上具有明显的优势。

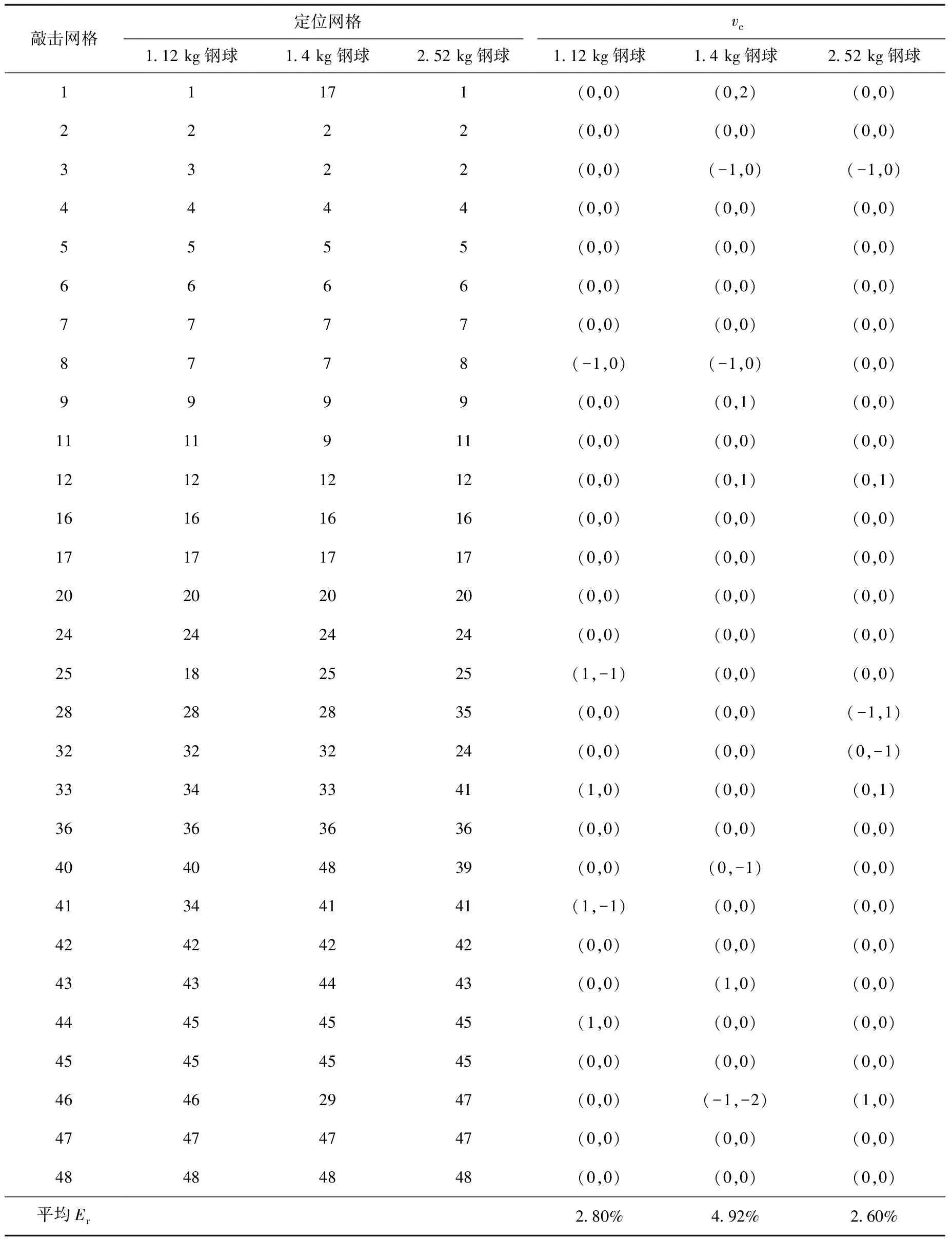
表2 小波尺度20下的定位结果

3.3 噪声冲击实验分析

图4为锅炉背景噪声的时域和频域图。可看出，噪声信号的频域范围较宽，主峰能量集中在6～8 kHz频率范围内，其频谱结构与反应堆压力容器和蒸汽发生器内背景噪声的频谱结构基本类似，但主频较高(一般反应堆主频约为5～6 kHz)。

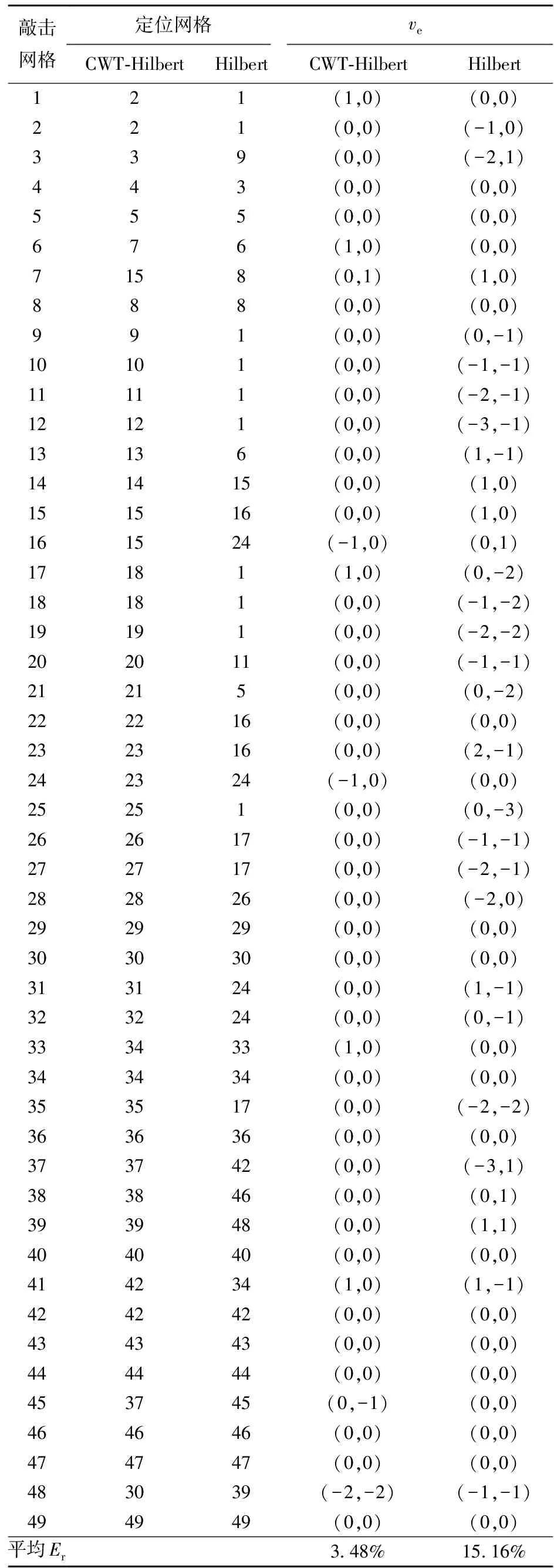
表3 不同到达时差估计方法定位结果

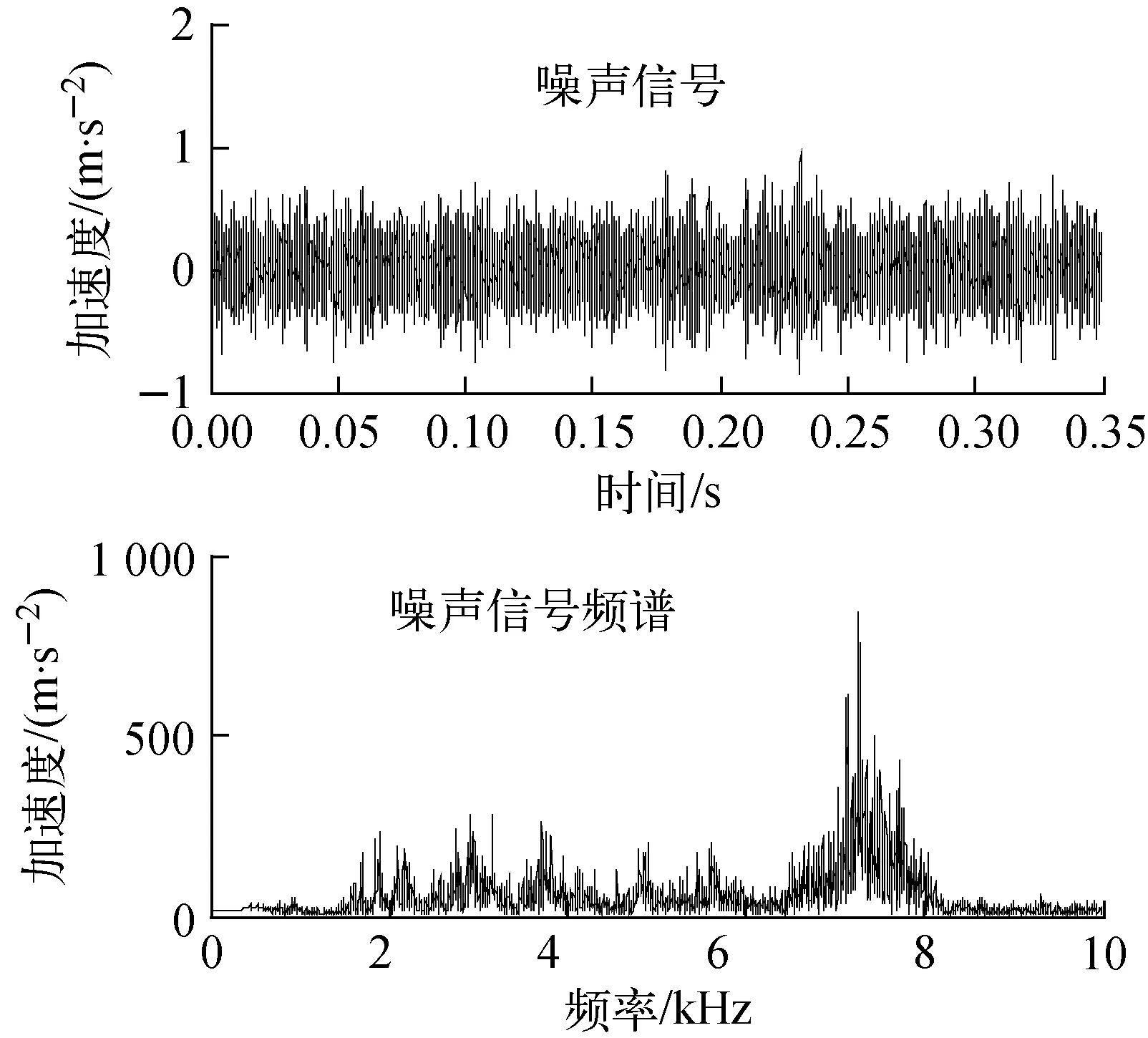
图4 锅炉背景噪声

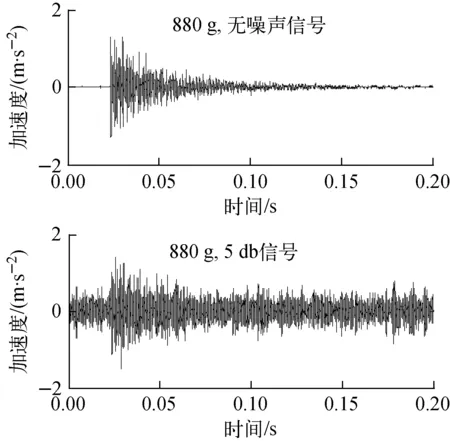
图5 880 g钢球冲击信号时域

图5为880 g钢球冲击信号不加噪声和信噪比为5 dB时的时域对比。表4为CWT-Hilbert和Hilbert包络线法对信噪比为5 dB的880 g钢球冲击信号的定位结果。从表4可看出，CWT-Hilbert包络线法的抗噪声干扰能力较Hilbert包络线法的强，这是由于CWT根据冲击信号主频带对信号实现细化，从而降低了非主频带内信号的干扰。表5为基于CWT的3种不同时差估算方法对信噪比为5 dB的880 g钢球冲击信号的定位结果。从表5可看出，CWT-Hilbert包络线法的定位误差小于其他两种方法，该方法具有较好的抗噪声干扰能力。原因是CWT-Hilbert包络线法是取Hilbert包络线的首个峰值所对应的时间为冲击信号的到达时刻，而其他两种方法则是取信号的过零点，且Hilbert包络线法采用的是能量最大的弯曲波成分的速度，而经CWT后的信号能很好地满足该条件。

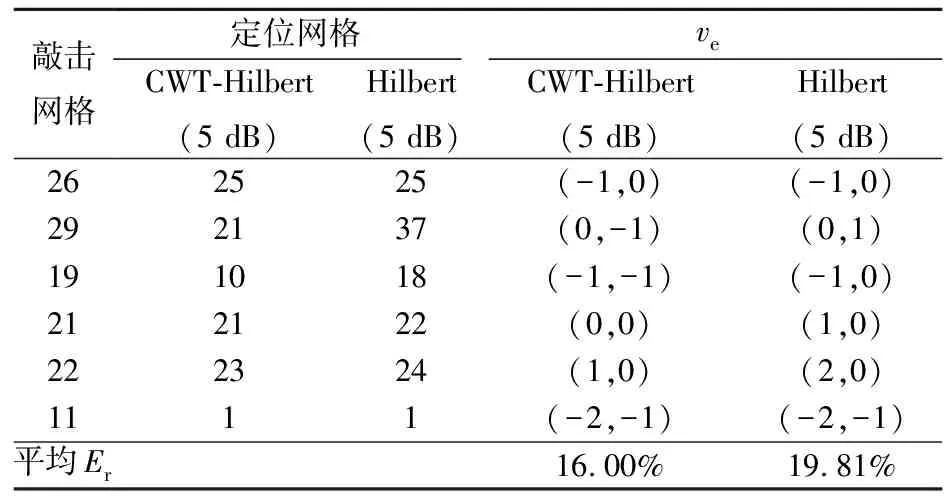
表4 基于CWT-Hilbert和Hilbert包络线法的880 g钢球尺度8下的定位结果

在信噪比为0 dB时，CWT-累加和法和CWT-均方根法均无法确定信号的到达时刻，CWT-Hilbert包络线法均在大质量冲击信号下才能有效。因为小质量信号的能量集中在高频段，大质量冲击信号的能量集中在低频段，而锅炉背景噪声的能量集中在高频段。当小质量冲击信号叠加上噪声时，噪声的能量将会淹没冲击信号的能量，即随信噪比的减小，信号的能量特征越来越不明显，从而更不易辨识。当大质量冲击信号叠加上噪声时，由于其能量集中频段间隔大，再加上小波高尺度变换的作用，其对冲击信号的能量特征影响相对较小。Hilbert包络线法是取能量轮廓线的峰值，所以在低信噪比的情况下仍能确定大质量冲击信号到达测量点的时刻。表6为9 kg钢球的冲击信号在信噪比为0 dB时的定位结果。从表6中可看出，CWT-Hilbert包络线法在信噪比为0 dB时仍能较准确实现定位。

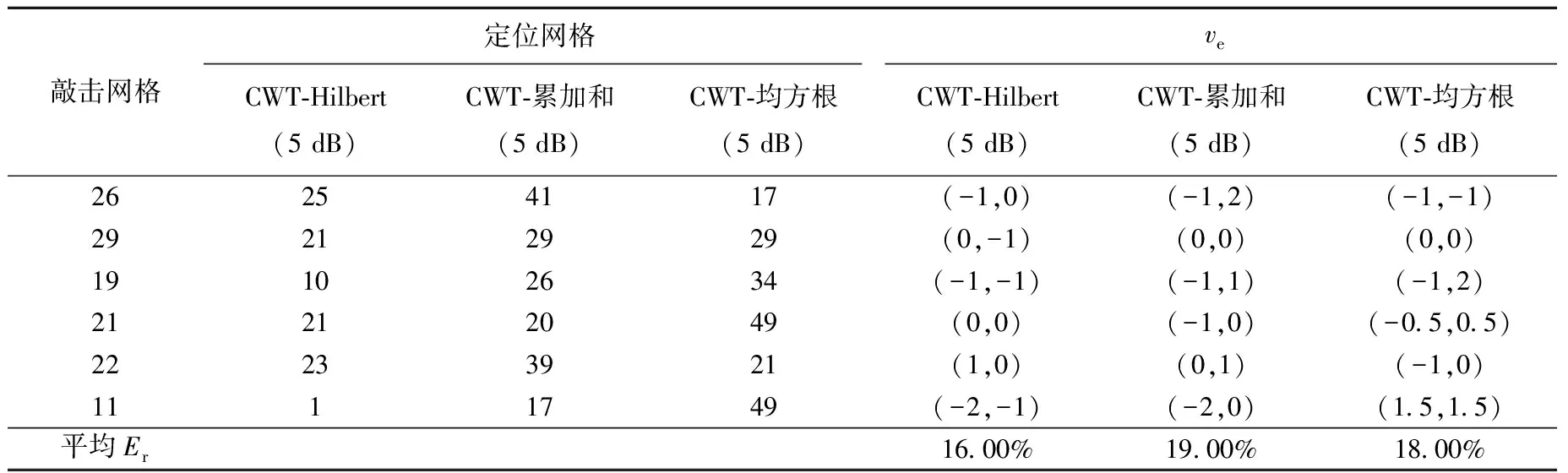
表5 基于CWT的880 g钢球尺度8下的定位结果

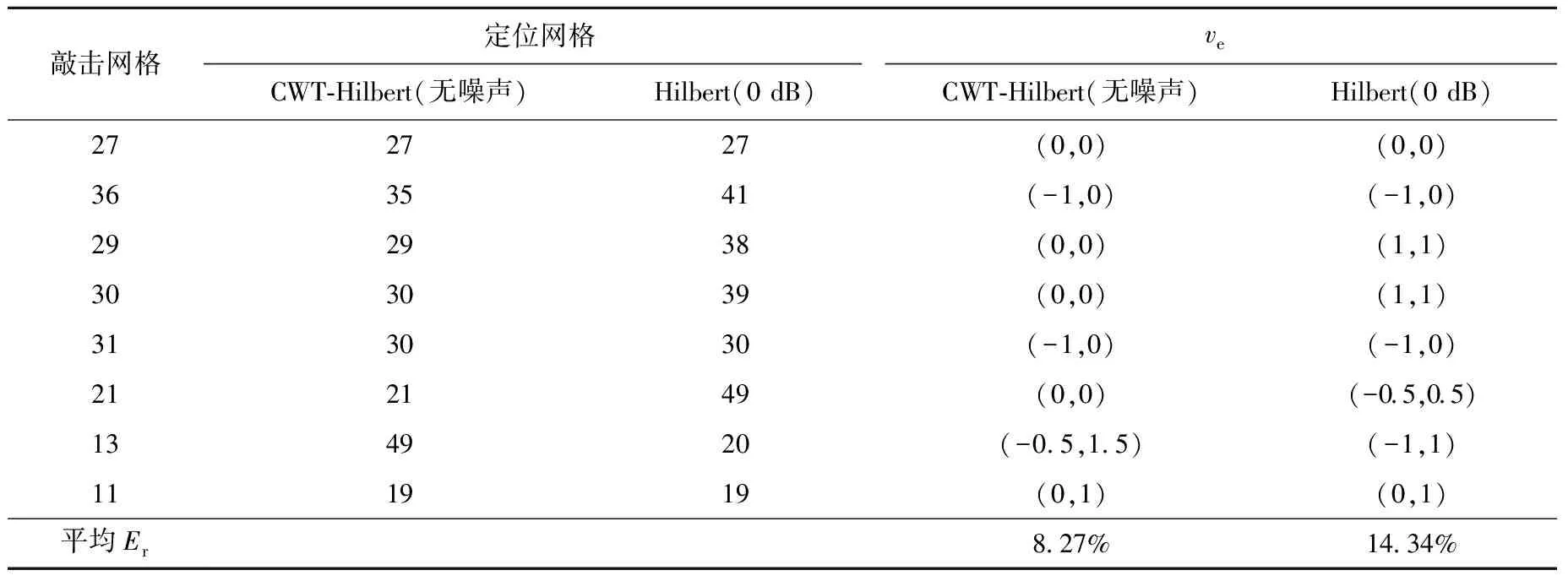
表6 9 kg钢球尺度20下的定位结果

4 结论

由实验结果可知，采用CWT-Hilbert包络线法来实现松动部件定位的效果较好、定位精度高、抗噪声干扰能力强，具有较好的工程应用价值。该方法主要有以下优点：

1) 定位精度高。CWT在不改变信号能量的前提下，能实现信号时-频域的局部化。CWT细化了冲击信号主频带内的信号，使弯曲波的频率成分变得集中，提高了波速的估算精度。且Hilbert包络线法采用的是能量最大的弯曲波成分的速度，而经连续小波变换后的信号能满足该条件，从而提高了定位精度。

2) 抗干扰能力强。在信噪比为5 dB的情况下，能较准确地实现松动件的定位，在信噪比为0 dB时，对于大质量的冲击信号仍能较准确地实现定位。

3) 对到达时刻的判断更简单易行。Hilbert包络线法取Hilbert包络线的首个峰值为冲击信号的到达时刻，由于峰值易于识别，所以对于阈值的设定和调节较简单易行。而累加和法和均方根法则是取信号过零点为冲击信号的到达时刻，在加入噪声的情况下，对阈值的设定和调节均较难。

参考文献：

[1] ZIOLA S M. Source location in thin plates using cross-correlation[J]. Journal of the Acoustical Society of America, 1991, 90(5): 2 551-2 556.

[2] PARK G Y, CHEON S W, LEE C K. An estimation method for impact location of loose parts[J]. Progress in Nuclear Energy, 2006, 48(4): 360-370.

[3] FIGEDY S, OKSA G. Modern methods of signal processing in the loose part monitoring system[J]. Progress in Nuclear Energy, 2005, 46(3-4): 253-267.

[4] 方力先，陈仲仪. 小波变换在核电站一回路松动部件定位的应用研究[J]. 核科学与工程，2000，21(1):50-53.

FANG Lixian, CHEN Zhongyi. The study on the application of wavelet transformation in reactor’s loose parts locate[J]. Chinese Journal of Nuclear Science and Engineering, 2000, 21(1): 50-53(in Chinese).

[5] 杨将新，郑华文，曹衍龙，等. 基于希尔伯特变换的核电站松动件定位方法[J]. 机械工程学报，2009，45(12):232-236.

YANG Jiangxin, ZHENG Huawen, CAO Yanlong, et al. Estimation method for impact location of loose parts based on Hilbert transform[J]. Journal of Mechanical Engineering, 2009, 45(12): 232-236(in Chinese).

[6] 程正兴. 小波分析算法与应用[M]. 西安：西安交通大学出版社，1998：33-35.

[7] 李楠，周波. 信号处理中各种频率以及小波尺度的关系[J]. 电气电子教学学报，2008，30(6)：15-17.

LI Nan, ZHOU Bo. Relations among the different frequencies and wavelet scale in signal processing[J]. Journal of EEE, 2008, 30(6): 15-17(in Chinese).

[8] BO Lin, LIU Xiaofeng, QIN Shuren. Improved method for Hilbert instantaneous frequency estimation[J]. Chinese Journal of Mechanical Engineering, 2007, 20(6): 98-102.

[9] DUGUNDJI J. Envelopes and pre-envelopes of real waveforms[J]. IRE Transactions on Information Theory, 1958, 4(1): 53-57.