城市无控制交叉口通行能力计算方法

李爱增, 宋向红

(1.河南城建学院 交通运输工程学院, 河南 平顶山 467036;2.平顶山教育学院 计算机系, 河南 平顶山 467000)

城市无控制交叉口通行能力计算方法

李爱增*1, 宋向红2

(1.河南城建学院 交通运输工程学院, 河南 平顶山 467036;2.平顶山教育学院 计算机系, 河南 平顶山 467000)

分析城市无控制交叉口的交通流运行特征,给出了考虑当量人群流影响时直行组合车流和左转组合车流的冲突交通流简化模式.考虑机动车流和当量人群流的到达模式,利用车队分析法得到了直行组合车流和左转组合车流的通行能力计算公式.采用最小跟车时距理论,得到右转车流不受当量人群流影响时的通行能力计算公式和受当量人群流影响时通行能力修正系数的计算公式.在上述分析的基础上得到了城市无控制交叉口的通行能力计算模型.实例分析表明,本文所提出的计算方法符合我国城市道路交通流的运行特点,计算过程较迭代方法简单.

交通工程;城市无控制交叉口;通行能力;车对分析法;跟车时距;组合车流

1 引 言

城市无控制交叉口是指两相交的城市道路等级基本相同、各入口车辆进入交叉口时均需停车等待寻找对方车流间隙通过的交叉口,类似于国外的四 路 停 车 交 叉 口 (All-way stop-controlled intersections).对于无控制交叉口的通行能力计算,国内学者较多以车队分析法进行研究.文献[1]采用车队分析理论,假设交叉口各进口车流的到达模式服从移位负指数分布,推导了公路交叉口两单向直行车流的通行能力计算模型.文献[2]在文献[1]的基础上,考虑有对向车流和转弯车流的情况,推导了两双向道路相交时的通行能力计算模型.还有其他学者[3]利用车队分析理论进行研究.除了车队分析法外,也有个别学者利用冲突技术对无控制交叉口的通行能力进行分析[4].上述研究以机动车流为研究对象,分析了无控制交叉口的通行能力计算过程.

国外对于无控制交叉口的通行能力计算,从计算方法上可分为有迭代和无迭代两种.迭代算法以美国 HCM2000[5]为代表,将交叉口的车辆运行状态分为两种模式,通行能力计算以表格的形式按四种逐渐复杂的状态进行,过程较为复杂,且没有考虑非机动车、行人对机动车通行的影响.除了迭代算法外,还有学者[6,7]考虑转向车流的影响,基于附加冲突交通流分析,提出了基于流向的通行能力计算模型,计算过程不需要迭代.文献[8]研究高流率条件下车辆的驶离车头时距等因素,提出了通行能力调整系数,该方法将摩托车和自行车视为轻型车,没有考虑行人的影响.

经观察,城市无控制交叉口一般由两支路相交而成,交叉口处有较多的非机动车和行人,由于机动车车速较低,非机动车、行人和机动车在通过交叉口时均须找对方的可穿越间隙通过.另外,如果无控制交叉口距上游信号交叉口较近,上游信号灯会影响无控制交叉口的机动车流到达模式.因此,在城市道路中,一方面无控制交叉口的车流到达模式不一定服从移位负指数分布,另一方面,城市道路中存在的大量非机动车和行人对交叉口处机动车的通行产生了较大影响.下述分析将以已有研究成果[1,2]为基础,考虑上述城市道路交叉口的具体特征,采用车队分析理论进行研究.

2 城市无控制交叉口交通流运行特征

2.1 非机动车和行人的通行特征

非机动车和行人在通过交叉口的过程中,存在着叠加现象.以当量人群描述其通行特征,研究表明,由非机动车和行人组成的当量人群,其群个数与当量人数之间存在着如下关系[9]:

式中 yg——15 min 群个数;

x ——15 min 当量人数.上述当量人数为根据自行车、电动车和行人间的换算系数值,即 Cb=1.67、Ce=1.58、Cp=1,将自行车和电动车换算为行人后的“人数和”.

2.2 交通流到达时距分布

研究表明[10],当无控制交叉口距上游信号交叉口在 0.4 km 以内时,到达无控制交叉口的车头时距服从 M3分布.当与上游信号交叉口间距大于0.4 km 时,若到达流量小于 500 veh/h,车头时距服从移位负指数分布; 若到达流量大于 500 veh/h,车头时距服从 M3 分布.对于无控制交叉口处由非机动车和行人组成的当量人群,其到达时距服从移位负指数分布.

2.3 交通流冲突分析

城市无控制交叉口各流向冲突状况如图1所示.

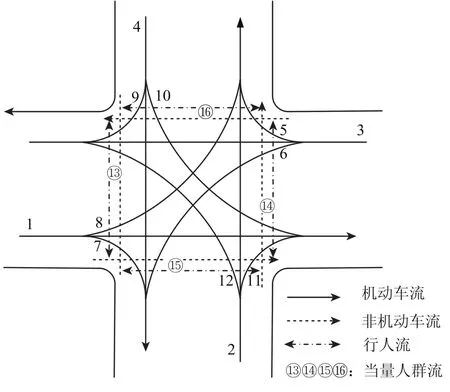
由图1 可知,对于直行和左转车流来说,其通过交叉口的过程中除了要穿越四个机动车流冲突点外,还要穿越两个当量人群流冲突点.对于右转车流来说,其通过交叉口的过程中和机动车流之间只存在着分合流的情况,但右转车流在通过交叉口的过程中均要经历两个当量人群流冲突点.

3 城市无控制交叉口通行能力计算方法

3.1 城市无控制交叉口通行能力的定义

城市无控制交叉口的通行能力定义为交叉口各进口各流向的通行能力的和;各流向的通行能力为考虑各进口的交通流到达模式、当量人群流对机动车的影响及各冲突交通流之间的相互影响,并假设各流向具有专用车道时,各流向在单位时间内所能通过的最大小汽车数量.

3.2 直行车流通行能力分析

记单向交通流车头时距分布的残存函数(survivor function)[11]为 R(t),a、b 组 合 车 流 延 迟分布的残存函数为 Xa,b.

3.2.1 直行组合车流 1、3 的通行能力

由图1 可知,直行组合车流 1、3 通过交叉口的过程中,与其可能发生冲突的交通流包括机动车流2、4、6、8、10、12 和当量人群流 13、14.将 1、3车流通过交叉口时需穿越的交通流做如下简化,如图2 (a)所示.A车流为4车流,B车流为6车流和10车流,C车流为8车流和12车流,D车流为2车流,E为当量人群流 13,F为当量人群流14.

采用车队分析法,计算得 1、3 车流的通行能力计算公式为

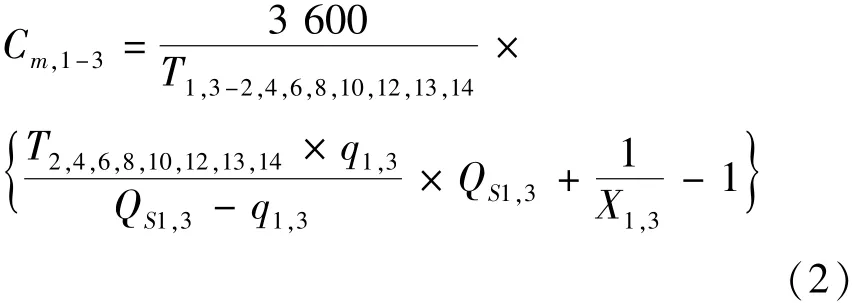
式中 T1,3-2,4,6,8,10,12,13,14——1,3 及 2,4,6,8,10, 12,13,14 流向各通过一列车队所需时间(s);

T2,4,6,8,10,12,13,14——2,4,6,8,10,12,13,14流向通过一列车队所需时间(s);

q1,3——1,3 组合车流的到达率(pcu/s);

Qs1,3——1,3 组合车流的饱和流率(pcu/s);

X1,3——1,3 组合车流延迟分布的残存函数.

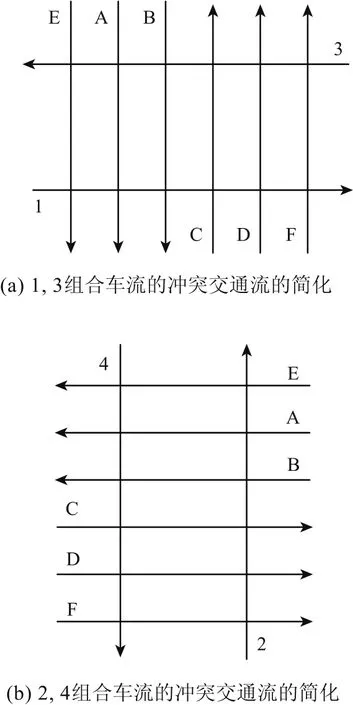
图2 直行车流的冲突交通流简化图Fig.2 Simplified sketch of through vehicles'conflicting traffic flow

3.2.2 直行组合车流 2、4 的通行能力

直行组合车流 2、4 在通过交叉口的过程中,与其可能发生冲突的交通流包括机动车流 1、3、6、8、10、12 和当量人群流 15、16.将 2、4 车流通过交叉口时需穿越的交通流做如下简化,如图2(b)所示. A 车流为 3 车流,B 车流为 6 车流和 12 车流,C 车流为 8 车流和 10 车流,D 车流为 1 车流,E 为当量人群流 16,F 为当量人群流 15.

采用车队分析法,得 2、4 车流的通行能力计算公式为

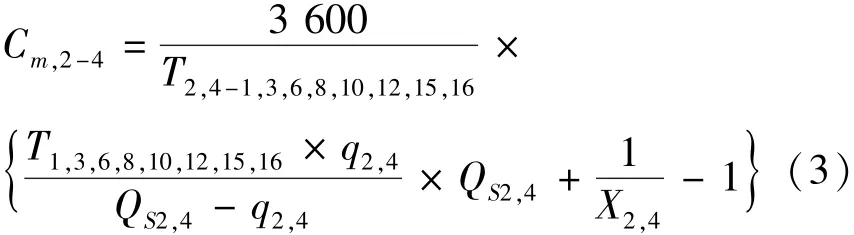
式中 T2,4-1,3,6,8,10,12,15,16——2,4 及 1,3,6,8,10, 12,15,16 流向各通过一列车队所需时间(s);

T1,3,6,8,10,12,15,16——1,3,6,8,10,12,15,16流向通过一列车队所需时间(s);

q2,4——2,4 组合车流的到达率(pcu/s);

QS2,4——2,4 组合车流的饱和流率(pcu/s);

X2,4——2,4 组合车流延迟分布残存函数.

3.2.3 直行冲突交通流的可能组合分析

与直行组合车流 1、3 相冲突的交通流包括:2、4、6、8、10、12、13、14,它们中的任何一个都可以构成 1、3 车流的冲突交通流.但在这些冲突交通流之间也存在着可能的冲突组合,在某一时刻只可能有某种组合作为 1、3 组合车流的冲突交通流通过,它们之间的可能组合如表1所示.

同理,直行组合车流 2、4 的冲突交通流可能组合如表1所示.

3.3 左转车流通行能力分析

3.3.1 左转组合车流 6、8 的通行能力

左转组合车流 6、8 通过交叉口的过程中,与其可能发生冲突的交通流包括机动车流 1、2、3、4、10、12 和当量人群流 13、14、15、16.按照前述相似的简化方法,将 6、8 车流通过交叉口时需穿越的交通流做如下简化,如图3(a)所示.其中 A 车流为 2车流和 3 车流,B 车流为 10 车流,C 车流为 12 车流,D 车流为 1 车流和4 车流,E 为当量人群流 14、16,F 为当量人群流 13、15.

和前述分析方法相同,得 6、8 车流的通行能力计算公式为

式中 T6,8-1,2,3,4,10,12,13,14,15,16——6,8 和 1,2,3,4, 10,12,13,14,15,16 流向各通过一列车队所需时间(s);

T1,2,3,4,10,12,13,14,15,16——1,2,3,4,10,12, 13,14,15,16 流向通过一列车队所需时间(s);

q6,8——6,8 组合车流的到达率(pcu/s);

QS6,8——6,8 组合车流的饱和流率(pcu/s);

X6,8——6,8 组合车流延迟分布的残存函数.

3.3.2 左转组合车流 10、12 的通行能力

左转组合车流 10、12 通过交叉口的过程中,与其可能发生冲突的交通流包括机动车流 1、2、3、4、6、8 和当量人群流 13、14、15、16.按照前述相似的简化方法,将 10、12 车流通过交叉口时所需穿越的交通流做如下简化,如图3(b)所示.其中 A 车流为3 车流和4 车流,B 车流为8 车流,C 车流为6 车

表1 直行组合车流的可能冲突组合Table1 Possible conflicting combination of through combined traffic flow

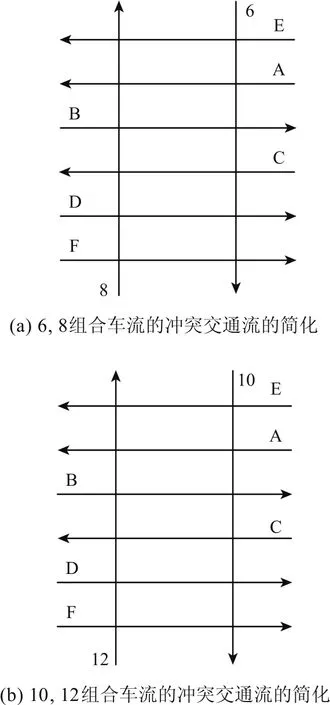
图3 左转车流的冲突交通流简化图Fig.3 Simplified sketch of left-turn vehicles'conflicting traffic flow

流,D 车流为 1 车流和 2 车流,E 为当量人群流 13、16,F 为当量人群流 14、15.

得 10、12 车流的通行能力计算公式为

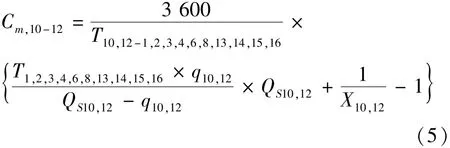
式中 T10,12-1,2,3,4,6,8,13,14,15,16——10,12 和 1,2,3, 4,6,8,13,14,15,16 流向各通过一列车队所需时间(s);

T1,2,3,4,6,8,13,14,15,16——1,2,3,4,6,8,13, 14,15,16 流向通过一列车队所需时间(s);

q10,12——10,12 组合车流的到达率(pcu/s);

QS10,12——10,12 组合车流的饱和流率(pcu/s);

X10,12——10,12 组合车流延迟分布的残存函数.

3.3.3 左转冲突交通流的可能组合分析

同理,左转组合车流的可能冲突交通流组合如表2所示.

3.4 右转车流通行能力分析

理论上各入口右转车流不必穿越其它车流,可将右转车流不受当量人群流影响或影响很小时的饱和流率作为右转车流的可能通行能力,然后再考虑当量人群流的影响.

3.4.1 不考虑当量人群流影响时的右转车流通行能力

记右转车流的可能通行能力为 Cp,i,i=5,7,9, 11, 则式中 tfi——右转车流不受当量人群流影响或影响很小时的跟车时距(s).

3.4.2 当量人群流对右转车流通行能力的影响

记当量人群流对右转车流 5、7、9、11 的影响系数为 Ki,pb,i=5,7,9,11,则

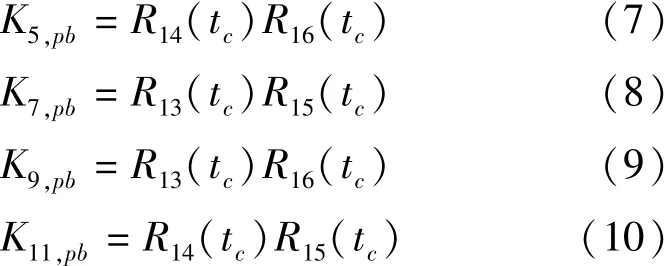
式中 Ri(tc) —— 当量人群流的群时距分布残存函数,i=13,14,15,16.

则考虑当量人群流影响时,右转车流的实际通行能力为

式中 i——右转交通流编号,i=5,7,9,11.

表2 左转组合车流的可能冲突组合Table2 Possible conflicting combination of left-turn combined traffic flow

3.5 各流向通行能力计算中的参数确定

3.5.1 冲突交通流残存函数值的确定

在直行和左转车流的通行能力计算中,记组合车流为 A 车流,冲突车流为 B 车流,二者的残存函数值分别为 XA和 XB.在 B 车流中共存在着 14 种可能的冲突组合,记其残存函数值为 XBi,i=1 ～14,在进行 XB计算时,可根据这 14 种可能组合的交通 量 求其权 重 wi,i=1 ～ 14, 从而 得到

对于左转组合车流 6、8 的第 14 种冲突交通流组合 13、14、15、16,由于左转车流 6 只需穿越 14、15,左转车流 8 只需穿越 13、16,故取 XB14=(X14,15+X13,16)/2.同理对于左转组合车流 10、12 的第 14种冲突交通流组合13、14、15、16,取 XB14=(X14,16+ X13,15)/2.

3.5.2 冲突交通流交通量、饱和流率、最小车头时距的确定

直行和左转组合车流的冲突交通流分别为8个和10个,在求冲突交通流的交通量和饱和流率时,可按照各种组合状况的权重求其加权平均值作为冲突交通流的交通量和饱和流率值.由于各冲突交通流组合的最小时距 tpi=0,i=1 ～ 14,因此对于整个冲突交通流来说,可取其最小车头 时 距 tpB=0.

3.6 不同交通流到达模式下的通行能力分析

3.6.1 组合交通流延迟分布的残存函数

由前述分析,城市无控制交叉口处当量人群流的群时距服从移位负指数分布,而机动车流的车头时距可能服从移位负指数分布,也可能服从 M3 分布.因此,各冲突交通流组合的时距分布状况有三种.

(1)各组合车流的车头时距均服从移位负指数分布.

当某一车流 i的车头时距服从移位负指数分布时,车头时距分布和延迟分布的残存函数分别如式(12)、式(13)所示.

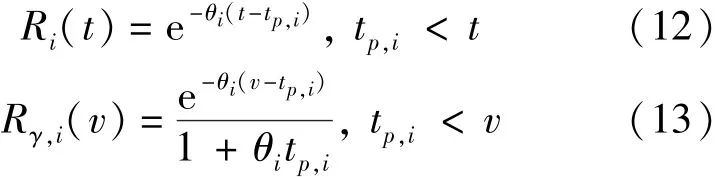
式中

θi—— 尺度参数,θi= λi/(1- λitp,i);

tp,i——最小车头时距(s);

λi——单位时间间隔的车辆到达率(veh/s).

当组合车流的车头时距均服从移位负指数分布时,记其为 Ik系列,由其叠加形成的延迟分布的残存函数为

式中 各符号意义同前.

(2)各组合车流的车头时距均服从 M3 分布.

当某一车流 i的车头时距服从 M3 分布时,车头时距分布和延迟分布的残存函数分别如式(15)、式(16)所示.

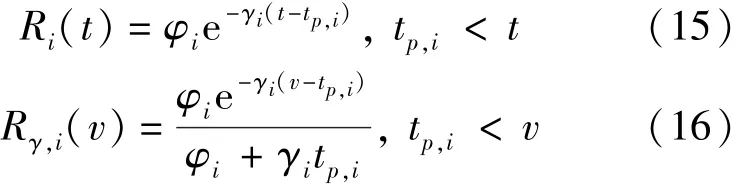
式中 φi——车队中自由车流比例;

γi——衰减常量,

qi——车流到达率(veh/s);

其它符号意义同前.

当组合车流的车头时距均服从 M3 分布时,记其为 Ik系列,由其叠加形成的延迟分布的残存函数为

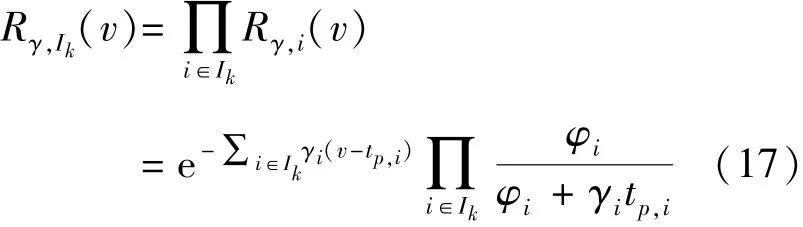
式中 各符号意义同前.

(3)组合车流中部分车流的车头时距服从移位负指数分布,部分车流的车头时距服从 M3分布.

当组合交通流的车头时距服从移位负指数分布时,记其为 Ik1系列,服从 M3 分布时,记其为 Ik2系列,则由这些组合车流叠加形成的延迟分布的残存函数为

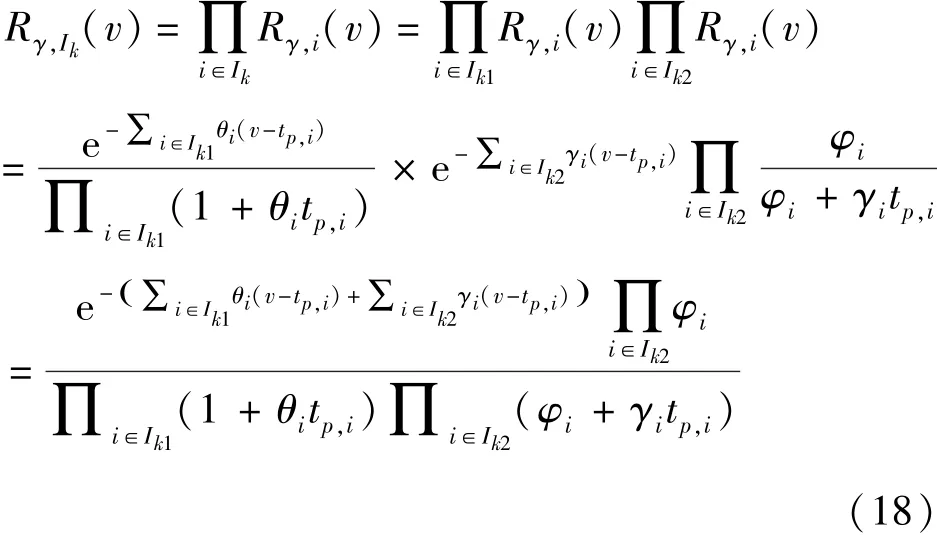
式中 各符号意义同前.

3.6.2 不同交通流到达模式下的通行能力分析

城市无控制交叉口各流向通行能力可按式(2)-式(11)进行计算.计算时由于组合车流的延迟分布的残存函数可能不同,统一记为 XCom,则

当组合车流的车头时距均服从移位负指数分布时,由式(14)可得

式中 tc——车辆穿越时的临界间隙值(s);

其它符号意义同前.

当组合车流的车头时距均服从 M3 分布时,由式(17)可得

式中 各符号意义同前.

当组合车流中部分车流的车头时距服从移位负指数分布,部分车流的车头时距服从 M3 分布时,由式(18)可得

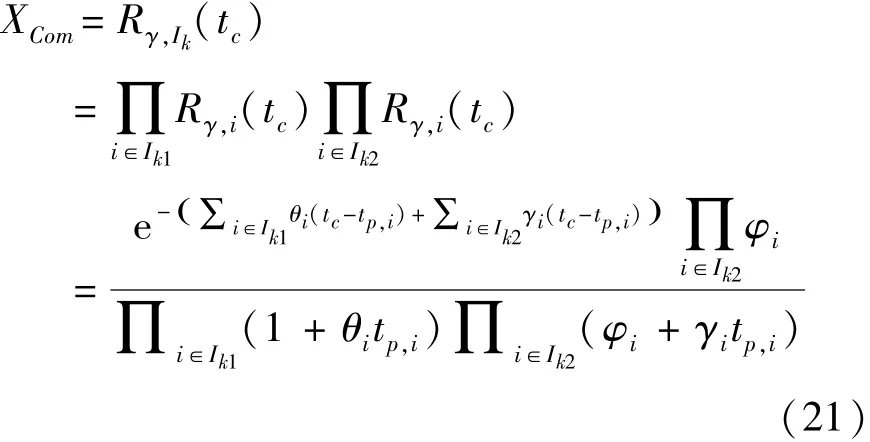
式中 各符号意义同前.

3.7 共用车道情况下的通行能力分析

当交叉口进口各流向没有专用车道时,可采用HCM2000[5]的分析方法,共用车道情况下进口道的通行能力可按式(22)进行计算.

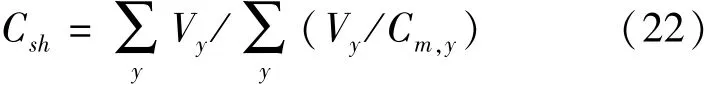
式中 Csh——共用车道的通行能力(pcu/h);

Vy——共用车道中流向y的交通流率(pcu/h);

Cm,y——共用车道中流向y的通行能力(pcu/h).

4 算例分析

4.1 交叉口基本特征与流量状况

优越路-劳动路交叉口位于平顶山市中心商业区,两相交道路均为双向两车道,各进口均为左直右共用车道,该交叉口高峰小时机动车和当量人群的流量流向状况如图4所示.

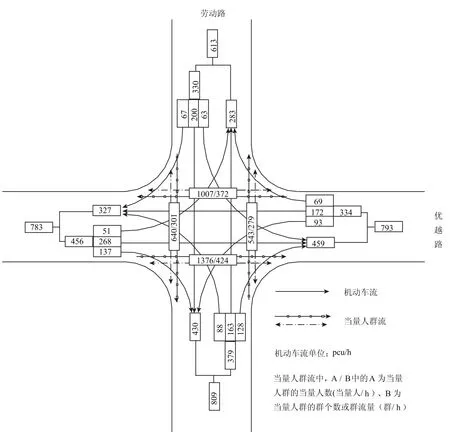
图4 高峰小时交通流流量流向图Fig.4 Traffic volume and direction in peak-hour

表3 临界间隙、跟车时距和最小车头时距值Table3 Critical-gap,follow-up time and minimum time-headway

表4 交叉口各进口及整个交叉口的通行能力值Table4 Capacity of intersection and each entrance

4.2 机动车流和当量人群流的到达时距分布

该交叉口北进口距上游信号交叉口 270 m,其它进口的相邻交叉口均为无信号交叉口.经分析,北进口的车头时距服从 M3 分布,其它进口的车头时距服从移位负指数分布.

4.3 交叉口通行能力计算

该交叉口机动车流穿越机动车流时的临界间隙、跟车时距和最小车头时距,以及机动车流穿越当量人群流时的临界间隙和跟车时距如表3所示.

经计算,该交叉口各进口及整个交叉口的通行能力值如表4 所示.由表4 可知,该交叉口高峰小时交通负荷较大,交通较为拥挤,和现场观测结果相同.

5 研究结论

(1)考虑当量人群流的影响,对直行组合车流和左转组合车流的冲突交通流进行简化,结合机动车流和当量人群流的到达模式,利用车队分析法得到直行组合车流和左转组合车流的通行能力计算公式.

(2)采用最小跟车时距理论,得到右转车流不受当量人群流影响时的通行能力计算公式和受当量人群流影响时通行能力修正系数的计算公式.

(3)在上述分析的基础上得到城市无控制交叉口的通行能力计算方法.实例分析表明,上述计算方法符合我国城市道路交通流的运行特点,计算过程较迭代方法简单.

[1] 王炜,高海龙,李文权.公路交叉口通行能力分析方法[M]. 北 京: 科 学 出 版 社,2001.[WANG W, GAO H L,LI W Q.Capacity analysis method of highway intersections[M]. Beijing: Science Press,2001.]

[2] 吴聪.有对向车流的平面十字交叉口通行能力研究[D]. 长春: 吉林大学,2002.[WU C.Research on capacity of crossing intersection considering opposing flow[D].Changchun:Jilin University,2002.]

[3] 卢树, 陆化普. 无控制交叉口通行能力计算方法[J]. 公路交通科技,2001,19(2):10-13.[LU S, LU H P. Capacity method for uncontrolled intersections[J]. Journal of Highway and Transportation Research and Development,2001,19 (2):10-13.]

[4] Li H Y,Tian Z,Deng W.Capacity of multilane allway stop-controlled intersections based on the conflict technique[J].Transportation Research Record,2011, 2257:111-120.

[5] TRB.Highway capacity manual(HCM)2000 (CHAPTER 17)[R].National Research Council, Washington,DC,2000.

[6] Wu N.Determination of capacity at all-way stop-controlled intersections[J].Transportation Research Record, 2000,1710:205-214.

[7] Wu N.Total capacities at all-way stop-controlled intersections:Validation and comparison of highway capacity manual procedure and addition-conflict-flow technique[J].Transportation Research Record,2002,1802:54-61.

[8] Dawkins J M.Analysis of stop-controlled intersections in the Caribbean:A case study of Kingston,Jamaica [D].Atlanta:Georgia Institute of Technology,1997.

[9] 李爱增,王炜,李文权.城市道路交叉口当量人群运行特征[J]. 交通运输工程学报,2010,10(3): 84-89.[LI A Z,WANG W,LI W Q.Running characteristics of equivalent people groups at urban road intersections[J]. JournalofTraffic and Transportation Engineering,2010,10(3):84-89.]

[10] 李爱增. 城市道路交叉口空间布局及其通行能力研究[D]. 南京: 东南大学,2008.[LI A Z.Research on lane distribution conditions and capacity of urban road intersections [D]. Nanjing: Southeast University,2008.]

[11] Finnish Road Administration.Capacity and level of service at finnish unsignalized intersections[R]. Helsinki,2004. [J].Regional Science and Urban Economics,2012, 42:166-176.

Capacity Calculation Method of Urban Road All-way Stop-controlled Intersections

LI Ai-zeng1,SONG Xiang-hong2
(1.School of Transportation Engineering,Henan University of Urban Construction,Pingdingshan 467036,Henan,China; 2.Department of Computer Science,Pingdingshan Institute of Education,Pingdingshan 467000,Henan,China)

By analyzing traffic flow running characteristics on urban road all-way stop-controlled intersections,the methods of simplifying conflicting traffic flows for through combined and left-turn combined vehicles are introduced with consideration of equivalent people groups'effect.Taking vehicles'and equivalent people groups'arriving mode into account,platoon analysis method is applied,capacity calculation models for through combined and left-turn combined traffic flows are established.Applying minimum follow-up time theory,capacity calculation models of right-turn traffic flows are obtained,and the adjustment factors are obtained as well with consideration of the equivalent people groups'effect.The capacity calculation models of all-way stop-controlled intersections are obtained.The case study indicates that the capacity calculation models are in accordance with the traffic flow running characteristics in China, and the calculation process is simpler than iterative method as well.

traffic engineering;urban road all-way stop-controlled intersections;capacity;platoon analysis method;follow-up time;combined traffic flow

1009-6744(2014)01-0200-09

U491.4

A

2013-07-30

2013-10-27录用日期:2013-11-15

国家自然科学基金(51208261);教育部社科基金(12YCZH062).

李爱增(1972-),男,河南汝州人,副教授,博士.*通讯作者:liaizeng@163.com