平面道路交叉口交通流波动特性分析

王志刚,石 琴,王楠楠,丁建勋

(合肥工业大学 交通运输工程学院,合肥 230009)

平面道路交叉口交通流波动特性分析

王志刚,石 琴*,王楠楠,丁建勋

(合肥工业大学 交通运输工程学院,合肥 230009)

为了研究平面道路交叉口区域交通流的波动特性,本文从频域的角度出发将交叉口区域交通流的波动划分为低频、中频和高频三种频率范围内的信号.研究分析发现,一般低频趋势信号可由交通需求变化引起的行驶工况缓慢变化;高频噪声信号由驾驶行为等随机扰动引起;中频波动信号由行驶过程中不断加速减速引起.由此提出了用去趋势波动分析法消除交通流信号的低频趋势,用小波分析方法将采集的数据中的高频噪声部分消除,在此基础上用频谱分析理论研究交叉口区域不同位置的波动特性.结果表明,波动最明显的位置在停车线附近.

交通工程;波动特性分析;频谱分析;平面交叉口;去趋势波动分析;小波分析

1 引 言

由于交通堵塞及交通信号灯的控制,城市道路行驶工况存在一定的不稳定性.这些不稳定行驶工况也被称作“时走时停”交通.多数车辆经过信号交叉口时会产生周期性延误,同时,汽车进入交叉口前的减速、停车和离开交叉口时的加速过程会使得交叉口交通流量呈现明显的波动现象.这种波动交通会造成驾驶员的乘车舒适性较低,行驶速度减慢,燃油消耗量增加及更多的交通排放.国外对于道路交通流的理论模型研究起步较早.Gazis 以及Gipps 通过建立各种非线性模型分析交通演变[1,2];Bando 通过建立最优的速度模型(OVM) 研究了时走时停交通[3,4].实证研究同样取得了丰富的研究成果,Kuhne 通过单一的正弦曲线拟合的速度曲线来分析波动特性的周期和振幅[5];Kerner、Helbing、 Rehborn 等人通过道路观测点的方法将波动形式分为不同的类别[6-8].Jin 等人通过参数仿真,研究了道路几何分布特征对波动特性的影响[9]; Cassidy 等通过检测器测到的各时间间隔实时流量与 15 min 平均流量的差值来研究排队内部的流量波动[10].国内对于道路行驶工况波动特性的研究近几年也比较多,唐铁桥等分析了两车道交通流模型的波动特性[11];董斌等对城市快速路的变特性进行了研究[12].上述研究基本是在时域内对道路交通流特性进行分析.本文从频域的角度研究,将交通流波动由三种频率范围内的信号叠加组成,即由低频趋势信号,高频噪声信号和中频波动信号组成[13].利用去趋势波动分析法消除各个数据点速度数据的低频趋势,用小波分析方法[14]将采集的数据中的高频噪声部分消除,用频谱分析理论确定各个交叉口前后不同数据点波动的主要幅度和周期.

2 理论基础

2.1 去趋势波动分析

去趋势波动分析法(DFA,De-trended Fluctuation Analysis) 能够很好地检测出非平稳数据的长程相关性等方面信息.通过 DFA 方法可以消除信号的局部趋势,避免了将时间序列的短程相关、非平稳性虚假地检测为长程相关性.

DFA 的计算步骤可分为四步:

第1步对于信号数组{xi}(i=1,2,…,N)生成累积差序列{y(k)}:

第2步把序列{y(k)} 分成 Ns=int(N/s) 个等长、连续且不重叠的子区间 vj(j=1,2,…,Ns),其中 s为每个子区间 vj的长度.

第3步在每个长度为 s 的区间 vj(j=1,2,…,Ns)内用最小二乘法拟合回归趋势函数为

式中 m 为回归趋势阶数,对于 p 阶 DFA 分析过程,简记为 DFAp.例如 p=1,p=2 可分别记为一阶去趋势波动分析DFA1(first-order de-trended fluctuation analysis) 和二阶去趋势波动分析DFA2(second-order de-trended fluctuation analysis). 消 除趋势后的序列差记为.对这 Ns个子区间计算方差:

第4步对所有子区间的方差取平均值,再计算方根得到 DFA 波动函数 F(s)为

改变指标尺度 s的值,F(s)将随着区间长度 s的增大而变大,可得到波动 F(s)关于区间长度 s的曲线.如时间序列长程相关,则他们满足

分别对 F(s)和 s求对数,得到双对数曲线,曲线的斜率就是标度指数 α,它体现了长程相关特性.

2.2 小波变换分析

小波分析是一种时、频多分辨分析方法.设ψ(t)∈L2(R),其傅里叶变换为 满足允许条件(完全重构条件或恒等分辨条件)时,则有

称ψ(t)为一个基本小波或母小波.将母函数 ψ(t)经伸缩和平移后得

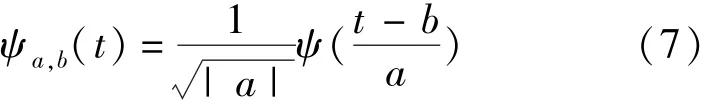
式中 a,b∈R;a≠0 称其为一个小波序列.其中 a 为伸缩因子,b 为平移因子.把 a 和 b 分别离散化为,其中 j∈Z,k∈R,扩展步长a0≠0 是固定值.一般取 a0＞1,对应的离散小波函数 ψj,k(t) 记为

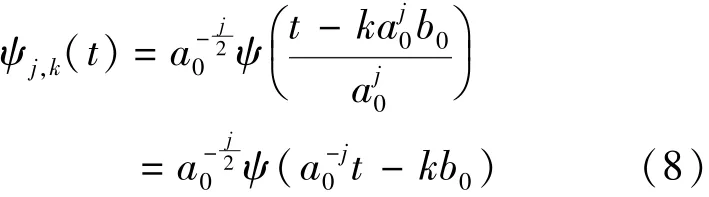
其重构公式(逆变换)为

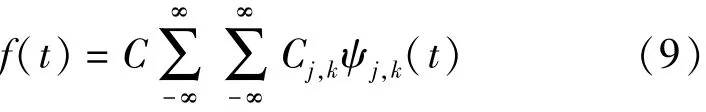
式中 C 是一个与信号无关的常 数,Cj,k为小波变换系数.

3 实例分析

3.1 数据采集方法

为了使采集到的数据具有一定的代表性,通过查阅合肥市交通路网图,选择了1个典型的交叉口进行试验.选取 450 m 的测试范围,每个数据点间的距离为 50 m,共 10 个数据点.包括交叉口停车线前 250 m,停车线后 200 m.测试时间为下午 17: 10-18:00.数据采集几何布局如图1 所示.

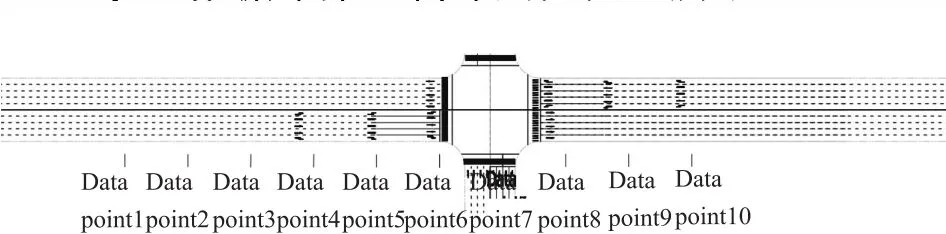
图1 数据采集几何布局Fig.1 Geometric layout of the data collection

3.2 数据处理

将采集的各个数据点的数据分别汇总在一起.为了方便处理,按时间间隔为 30 秒,数据的个数随时间的增加而增多,得到各个数据点的速度序列,如图2所示.图中中间横线为 3阶多项式拟合趋势.

图2 各数据点原始速度序列Fig.2 The speed sequence of each original data points

3.2.1 DFA 波动分析

DFA 波动分析方法就是消除各个数据点的速度序列的低频趋势.将步长分别设置为 6-40,分别求出拟合多项式阶数为 2,3,4 时的波动函数值,如图3所示.

波动函数 F(s)与 s的对数具有一定的线性关系.当时间步长 s相同时,DFA 阶数越高,局部趋势的拟合效果越好;波动函数 F(s)值越小,局部趋势拟合效果越好.但当阶数为 4 时,α 值变化过于平缓,在去除低频趋势后不易反映不同阶段原序列的波动特性.所以在用最小二乘法拟合低频趋势时,阶数选为3.根据数据的采集量,可将步长设置为20,这样既保证了足够的片段用于分析,也简化了计算.去除低频趋势后的各个数据点的速度序列如图4所示.

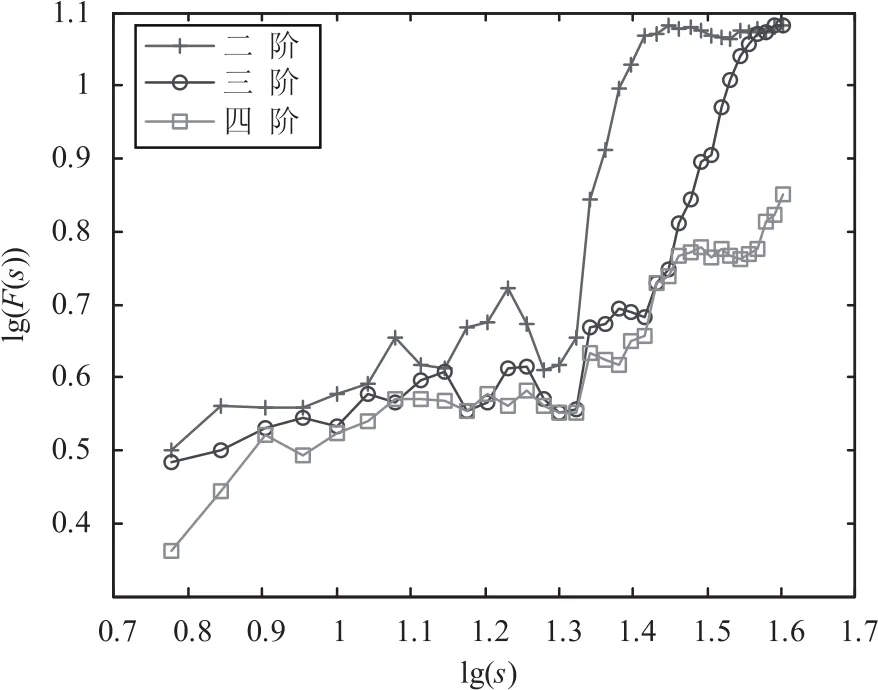
图3 不同阶数 DFA 波动函数 F(s)与步长 s的关系Fig.3 The relationship between DFA wave function and steps with different order

图4 去趋势后各数据点速度序列Fig.4 The de-trended speed sequence

由图4可以看出,原速度序列消除了低频趋势信号以后保留了波动特性.而且 DATA1 到 DATA5速度的最低值越来越小,说明车辆接近停车线时准备停车,DATA6 到 DATA10 速度最小值越来越大,说明车辆开始进入起步加速阶段.

3.2.2 小波分析和频谱变换

采用 Daubechies1 离散小波对各个数据点去低频趋势后的速度序列进行3尺度分解.再分别重构1-3 层逼近系数和细节系数.速度序列 DATA1 去趋势后小波分解图如图5所示.

由图5 可看出,细节系数突变频繁,反映了信号中的高频成分,代表着随机干扰信号.为了将高频扰动信号滤去,在重构原速度序列时可将低层细节系数滤去.由逼近系数重构原速度序列可得到滤去高频扰动信号的速度序列.通过以上步骤得到各个数据点的重构速度序列.

采用经典频谱分析获得各个数据点波动的主振幅和主周期.因为各个数据点数据是离散的,所以采用离散傅里叶变换(DFT)为

式中 N为序列长度.

图5 速度序列 DATA1 去趋势后小波分解图Fig.5 The wavelet decomposition figure of the de-trended speed sequence DATA 1

根据式(10)对各个数据点处理后的数据进行离散傅里叶变换,得到幅值谱图,如图6 所示.

图6 中两条竖直虚线分别为总能量的 20%, 80%.从图中可以看出,在交叉口上游,能量频带宽,即 80%e-20%e 对应的频率差值较大,这说明波动还不明显,而在交叉口附近,数据点 5 和数据点 6 处 80%e-20%e 对应的频率差明显减小,说明幅值波动较大,所以波动特性显著.而交叉口下游随着汽车匀速或匀加速行驶,幅值变换较小,80% e-20%e 对应的频率差也逐渐增大.

由图6各个数据点速度序列的频谱图可以看出,从数据点 1 到数据点 6 波动幅度逐渐增大,波动幅度最大的位置在数据点 6,即停车线附近,其主波动幅度值在 5.66 km/h.这反映了车辆在进入交叉口前减速,甚至怠速,直到绿灯又加速启动的过程.在交叉路口范围内(即数据点5 和数据点 6)保持较高的波动水平,离开交叉路口以后,波动幅度迅速减小,所以数据点 6到数据点 8幅度值减小,这反映了离开交叉路口车辆一般保持匀速或匀加速状态,但当远离交叉口时车辆又进入道路正常行驶的波动状态.

定义每个频率值对应的能量为 Ei=|xi(f)|2.求出每个数据点每个频率值对应的能量值,则总能量可表示为

4 研究结论

本文从频域角度来研究交叉口交通流波动特性,提出了一种新的能够很好地从具有低频趋势和高频噪声的原始数据中揭示交叉口波动特性的数据处理方法.通过经典频谱分析理论,确定了交叉口前后不同位置波动的主要幅度值,并分析造成该点信号波动的原因.但不同数据点的主要波动幅值是否是恒定不变的或者在很小的范围内浮动,将在以后的研究中进一步验证.

[1] Gazis D C,Herman R,Rothery R W.Nonlinear followthe-leader models of traffic flow [M].Operations Research,1961,9(4):545-567.

[2] Gipps P G,A behavioural car-following model for computer simulation[J].Transportation Research Part B,1981,15(2):105-111.

[3] Bando M,Hasebe K.Nakanishi K,et al.Analysis of optimal velocity model with explicit delay[J].Physical Review E,1998,58(5):5429-5435.

[4] Bando M,Hasebe K,Nakayama A,et al.Dynamical model of traffic congestion and numerical simulation [J].Physical Review E,1995,51(2):1035-1042.

[5] Kuhne R D.Freeway speed distribution and acceleration noise[C] ∥ Gartner N H,Wilson N H.(EDS), Proceedings of the 10th International Symposium on Transportation and Traffic Theory,1987:119-139.

[6] Kerner B.Empirical macroscopic features of spatialtemporal traffic patterns at highway bottlenecks[J]. Physical Review E,2002,65(4),046138.

[7] Helbing D,Hennecke A,Treiber M.Phase diagram of traffic states in the presence of inhomogeneities[J]. Physical Review Letter,1999,82(21):4360-4363.

[8] Kerner B,Rehborn H.Experimental properties of complexity in traffic flow[J].Physical Review E, 1996,53(5):R4275-R4278.

[9] JIN W L,ZHANG Y.Paramics simulation of periodic oscillations caused by network geometry [J]. Transportation Research Record,2005,1934(1): 188-196.

[10] Mauch M,Cassidy M J.Freeway traffic oscillations: observations and oredictions[C] ∥ Adelaide, Australis,International Symposium on Traffic and Transportation Theory.2002.

[11] 唐铁桥,黄海军.两车道交通流的波动分析[J].北京航空航天大学学报,2005,31(10):1121-1124.[ TANG T Q,HUANG H J.Wave properties of a traffic flow model for freeways with two lanes[J].Journal of Beijing University of Aeronautics and Astronautics, 2005,31(10):1121-1124.]

[12] 董斌.城市快速路交通流时变特性研究[D].长春:吉林大学,交通学院,2006,4.[DONG B.Study on the method of traffic state change time on urban expressway [D]. Changchun: Jilin University, 2006,4.]

[13] LI X P,PENG F,OUYANG Y F.Measurement and estimation oftraffic oscillation properties [J]. Transportation Research Part B,2010,44:1-14.

[14] 周伟.基于 MATLAB 的小波分析应用[M].西安:西安电子科技大学出版社,2010,6.[ZHOU W. Wavelet analysis and application based on Matlab [M].Xi'an:Xi'an University of Electronic Science and Technology Press,2010,6.]

Traffic Oscillation Properties on Roads Intersection

WANG Zhi-gang,SHI Qin,WANG Nan-nan,DING Jian-xun
(School of transportation Engineering,Hefei University of Technology,Hefei 230009,China)

This paper investigates traffic oscillation properties on roads intersection from frequency-domain perspective.According to the traffic oscillation characteristics on the roads intersection,a data sequence from the detector is the superposition of three sets of sinusoidal components,representing high-frequency noise,low-frequency trend and mid-range oscillations.The analysis found that the low-frequency signal relates to the changes of driving cycle generated by varying traffic demand,the high-frequency noise relates to the local random perturbations like driving behavior,and the mid-range oscillations relate to the frequently accelerating-decelerating operations in the driving cycles.So it proposes a de-trended fluctuation analysis to eliminate low-frequency velocity data trend,and use the Wavelet analysis method to eliminate high-frequency noise,and then apply the Frequency Analysis to study the wave characteristics for traffic stream on the different locations.The results show that the obviously wave at near the roads intersection.

traffic engineering;oscillation properties analysis;spectral analysis;intersection;De-trended fluctuation analysis;wavelet analysis

1009-6744(2014)01-0215-06

U491.115

A

2013-05-21

2013-08-26录用日期:2013-09-23

国家自然科学基金(71071044);国家自然科学基金青年基金项目(71201041);安徽省软科学计划研究项目(12020503062);教育部高等学校博士点新教师基金项目(20110111120023);外专千人计划(WQ20123400070)

作者介绍:王志刚(1988-),男,安徽池州人,硕士生.*通讯作者:shiqin@hfut.edu.cn