新城土地利用与交通模型
胡郁葱,陈海伟,梁枫明
(华南理工大学 土木与交通学院,广州 510640)
新城土地利用与交通模型
胡郁葱*,陈海伟,梁枫明
(华南理工大学 土木与交通学院,广州 510640)
为模拟新城土地利用的空间分布,运用离散选择理论,对 Lowry 模型中居住选址和活动选址的分布函数进行修正.将居民的选址效用定义为有关土地租金和交通区位的线性组合,建立家庭参与住宅和活动分配的平衡等式,构建新城土地利用与交通模型,并设计混合遗传算法进行求解.以广州南沙新城数据为支撑,对模型和算法进行参数标定及验证.结果显示:该模型对居住选址和活动选址的分布具有良好的解析能力,能为合理调配人口分布和就业格局提供依据,适用于新城发展的短期运行,具有较好的适应性和实用性.
交通工程;土地利用与交通模型;交通区位;新城;混合遗传算法
1 引 言
城市土地利用与交通系统的互动关系是交通规划的研究重点之一.在众多的城市土地利用与交通模型中,著名的 Lowry 模型直观地模拟了城市活动的基本行为,描述出土地利用与交通之间的关系.Lowry 模型由人口分配模型和重力模型两部分构成,其中,人口分配模型在给定基本人口的前提下推算出城市的服务人口和总人口,而重力模型用于确定的服务人口的就业区位和总人口的居住区位,再将结果反馈到人口分配模型中,从而将人口和就业的空间分布和土地利用融合在一个反复迭代的过程中[1].
Lowry 模型从建立至今,在国外城市的应用中不断获得完善和发展:数学规划、投入产出分析与该模型的融合使其具备了一定的经济行为基础[2];动力学原理和随机效用理论的引进[3],以及对交通阻抗函数的修正推动了交通模块的扩展[4].然而,Lowry 模型在国内的研究目前仍停留在模型综述、解析和理论探究阶段[5,6],适用性不强,主要原因是其中一些关键性问题至今仍未得到很好的解决:①对居住和就业的分布缺少清楚的行为解析;②避开价格因素,导致居住和活动供需之间不满足经济学理论的一致性均衡;③对交通系统的影响缺乏描述,未能体现交通区位对土地利用变化产生的反作用;④新城建设初期,许多住宅和店铺出现空置的情况,但目前各种形式的 Lowry 模型并未考虑到这个问题.
本文以解决上述问题为目标,运用离散选择理论解析人们居住和活动分布的选择行为,引入价格变量和交通区位分析土地租金、交通系统与土地利用之间的互动作用,建立家庭参与住宅和活动分配的平衡等式,构造适合新城规划的土地利用与交通模型,并设计混合遗传算法进行求解.所建立的模型不但具备 Lowry 模型的物质预测功能,而且能较好地体现土地利用与交通的双向反馈作用,且能适用于新城发展的短期运行.
2 模型构建
由于在新城建设初期,各类设施还不完善,导致住宅和店铺均可能出现空置的情况,从而使得居住和活动(包括就业就学、商业娱乐等)的供需呈现非均衡性.因此,在分析新城的土地利用时必须重新考虑居住和活动之间的关系.本文针对新城这一特性,结合土地价格和交通区位,构建新城土地利用与交通模型.
2.1 居住和活动选址的分布函数
由概率论可知:在 j区工作的人中,选择到 i区居住和到l区参与活动的概率为

式中 Pi/j——在 j区工作的人中,选择在 i 区居住的概率;
Pl/ji——在j区工作、i区居住的人中,选择到l区参与活动的概率;
其中,i区、j区和 l区可为同一个交通小区.
20世纪70年代以来,以 McFadden 为代表的一批学者引入经济学中的离散选择理论对交通问题展开了研究[7].该理论假设人们的选择行为总是以个人利益最大化为原则,即选择概率与效用最大值有关.效用是由选择枝本身的特性和个人属性共同决定的,但很难对影响效用的所有因素进行量测,因此,应该将不能观测的效用看作随机变量.令
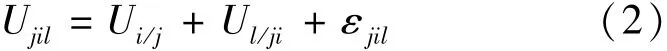
式中 Ujil——在 j区工作的人中,选择到 i 区居住和到l区参与活动的效用值;
Ui/j——在 j区工作的人中,选择在 i区居住的效用值;
Ul/ij——在 j区工作、 i 区居住的人中,选择到l区参与活动的效用值;
εjil——不能观测到的因素构成的效用随机项.
若不同的 εjil相互独立且服从 Gumbel 分布,可推出选择概率具有多项 logit模型形式[7]

式中 b——参数,b>0,可以推得,它与 εjil= ε 的均值和方差具有下列关系:

式中 γ——Euler 常数,约等于 0.577 2.
2.2 效用模型
为获得居住选址和活动选址的效用,需要引入区位理论.
区位理论是研究经济行为的空间选择理论,已被广泛应用于交通领域.该理论认为:交通小区的区位优势可以用“区位势”的概念来表征,它是交通小区出行产生和出行吸引大小的量化描述,表明人们选择区位居住、就业就学或商业娱乐等的喜好程度,与交通小区的交通可达性和用地聚类都成正比,其表达式为[8]

式中 r——交通可达性;
q——聚集规模质因子,如住宅和店铺密度等;
m——聚集规模量因子,如土地面积;
z——其他因素;
k——比例系数;
x、δ和 β——弹性影响系数.
此外,将相对区位势 Yi定义为交通小区 i的区位势 Qi与标准小区区位势 Q0的比值:

由式(5)和式(6)可得


居住地点的选择效用 Ui/j主要与小区 i的相对区位势能 Yi、平均房价 rHi及其他因素 Oi有关,可采用多元线性组合形式表示:
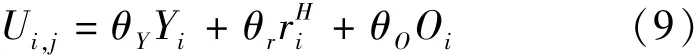
式中 θY、θr、θO——影响参数.
而活动地点的选择效用 Ul/ji主要与区 l 的相对区位势能 Yl和商品服务价格(可表示为平均店铺租金 rSl的函数)以及其他因素 Ol有关,同样可采用多元线性组合的形式:
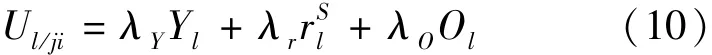
式中 λr、λr、λO——影响参数.
综合式(1)-式(10)可得到居住选址和活动选址的分布概率,它是相对区位势能、平均房价和平均店租的函数,即和
2.3 基于价格的新城居住与活动供需平衡一致性
假设小区 i的住宅数和店铺数分别为 Hi和Si.根据市场经济理论,住宅的供应者会根据市场价格决定其住宅是否出售或空置.由效用最大化理论可得小区i的住宅供应者选择出售其住宅而非空置的概率为二元 logit模型:
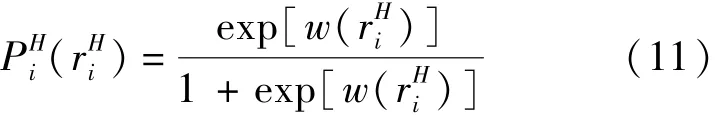
式中 w(·)——收益函数,即住宅出售相对于空置的差价,为的增函数.张友全等[9]的研究发现:住宅空置率与区域房价、交通可达性及其它因素有关.因此,收益函数可表示为,其中 a1、a2、a3、a4为影响参数
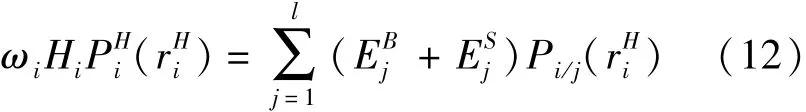
对于商业服务供应而言,店铺的老板根据租金、工资、货物价格和数量(可表示为租金和工资的函数)决定开业或关闭,并确定雇佣的最佳员工数.店铺开业而非关闭的概率为式中 e*i——小区 i店铺的最佳平均雇员数;
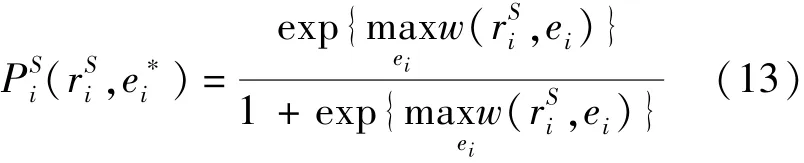
ei——小区 i店铺所需的平均雇员数;
则小区l活动选址的供需平衡关系为
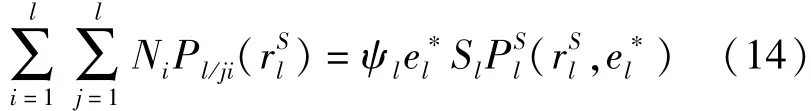
式中 Ni——小区 i的家庭人口;
ψl——小区 l每个雇员平均接待的顾客数,定为常数.
此外,假设小区 i每个家庭的平均人口数为ζi,则有下列等式:

2.4 约束条件
i分区的土地总面积可用下式表示:

式中 Li——i分区的土地总面积;
I——整个区域的分区数.

服务业的可利用面积少于剩余土地面积:
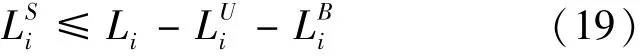
综上所述,合并式(1)-式(19)可得到 2I个非线性方程,包含 2I个未知数(分别为),其中 I为分区数量,这表明,在理论上该模型能求得唯一解.
3 混合遗传算法
求解非线性方程组的主要算法是拟牛顿法,但其收敛性对初始解的选择比较依赖,不合适的初始解容易导致收敛失败.近年快速发展的遗传算法具有较强的全局搜索最优解的能力,但该算法收敛较慢,编码长度对精度影响较大,在求解非线性方程组中,与传统方法相比并不具有优势[10].本文基于这两种算法各自的特点,从优化和迭代相结合的角度出发,设计了一种用于求解上述模型的混合遗传算法.
3.1 适应度函数
适应度函数描述了个体的适宜程度,可根据其适应度对个体进行评估,定出优劣.本文采用下列目标函数作为适应度函数:
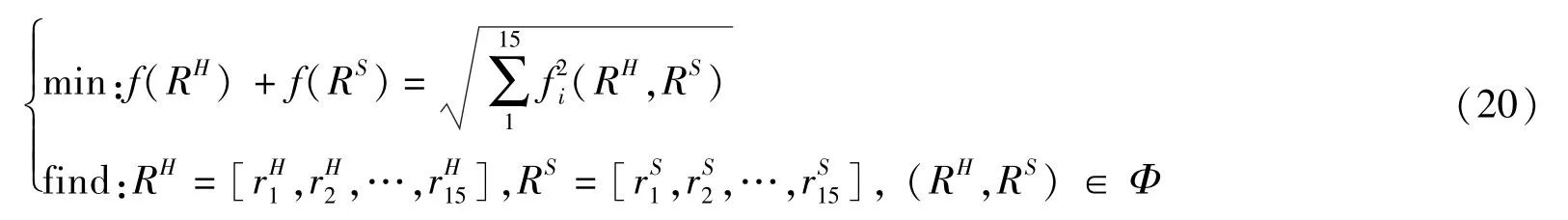
3.2 遗传算子
本文采用具有较高确定性和一定随机性的联赛竞争法为选择算子,其参数为联赛规模.为防止出现早熟现象,采用顶级尺度变换法(Top Scaling)对适应度函数进行尺度变换,变换参数为“数量(Quantity)”.而交叉算子采用启发式交叉,并用参数“ Ratio” 表示子辈与适应度较好的父辈之间的差距, 表 示 为 child=Ratio · (parent1-parent2)+ parent2.
此外,用确定性随机方向变异表示变异算子,算子描述为:设被选中变异个体的染色体为 Gk,随机产生一个扰动方向 uk,整个变异操作的过程是以 Gk为起点沿方向 uk寻求最优点作为新的染色体,即完成如下一维搜索运算:min g( λ)=f(Gk+ λuk),本文以黄金分割法搜索得到最优步长 λ0,则变异后的新染色体
3.3 收敛条件
对于非线性方程组的求解,收敛条件有两个:一个是进化到指定的最大代数;另外一个是误差控制,本文采用的收敛条件为
3.4 求解思路
先用遗传算法进行优化设计,找到最优解附近的一个解,将它作为拟牛顿法的初始解,并进行二次优化,从而找到全局最优解.其中,拟牛顿法通过用导函数的近似矩阵 Dk来代替导函数计算.其迭
Begin
确定设计变量上下限,随机产生初始父代群体,并对个体进行编码,设定算法基本参数.
While
评价群体:计算个体的适应度,确定最好和最差个体;
以交叉概率对群体进行启发式交叉运算,将父代和子代都加到子代群体;
以变异概率对群体进行高斯变异运算,将父代和子代都加入到子代群体;
依据顶级尺度变换的联赛竞争法选择算子,产生新的群体.
Until 满足迭代终止条件
将上述结果作为拟牛顿法的初始点,进行二次优化,找到全局最优解.
4 实例应用
本文以广州南沙新城的短期发展规划(2013-2020 年)为例,进行模型参数的标定、模型计算、检验及应用分析,2013 年为规划基础年,基础数据见表1.根据土地利用性质异同,并以河流和道路作为分界,将南沙新城划分为 15 个交通小区,如图1所示.

表1 2020年广州南沙新城规划基础数据(2013-2020 年)Table1 Basic data of Guangzhou Nansha new town planning in 2020(2013-2020)
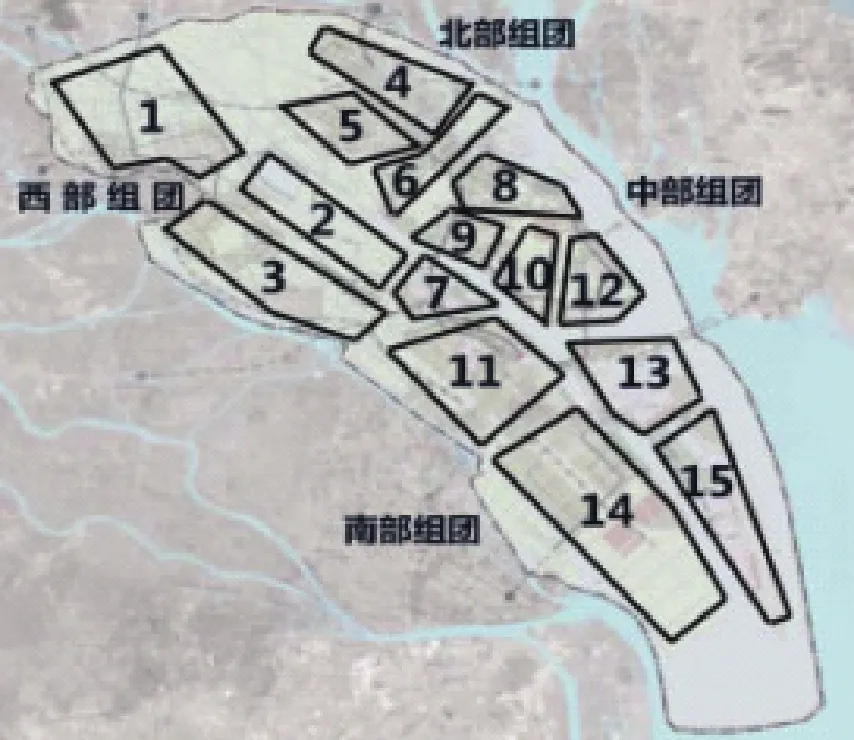
图1 南沙新城交通小区分布图Fig.1 Traffic zone in Nansha new town
4.1 相对区位势计算
本文分别选取住宅密度和活动密度(户/百平方米)作为交通产生和吸引的聚集质因子,并将居住用地面积和活动用地面积(平方千米)作为交通产生和吸引的聚集量因子.结合南沙新城未来发展定位,采用公交可达性表示交通可达性,定义为从某个交通小区出发,选择公交方式在 40 min 内可以到达的岗位数占全市岗位数的比值,其中人口岗位比参照国内外新城的数值(0.48-0.62),取值为 0.55.
采用多元线性回归方法,利用 SPSS 软件将弹性影响参数标定为 x=0.26,δ=0.21.由于交通小区8位于新城的中心,居住和活动用地规模最大,故选取交通小区8为标准小区.各个交通小区的区位影响因子和交通产生、吸引相对区位势能如表2所示.

表2 2020年广州南沙新城相对区位势及其影响因子Table2 Relative location and impact factor of Guangzhou Nansha new town in 2020
从表2可知,相对区位势大致呈现出从中心区向外围区递减的趋势,但是交通小区 4、11 和 14 的相对区位势能却比较高,主要是由于这三个小区分别位于北部组团、中部组团和南部组团的中心,人口和活动聚集密度大且公交可达性较好,体现出交通小区本身土地利用的特点和交通设施的发达水平.
4.2 选址效用参数和收益参数标定
由于个人收入和停车的便捷程度对居住地点和活动出行的选择影响较大,因此,本文将人均收入作为居住选址的其他影响因素 Oi,以停车位数作为活动选址的其他影响因素 Ol,其中,停车位数根据《广州市停车配建指标实施指南》求得.基于南沙现状数据,采用增长率法和国内外同类新城对比法,初步确定 2020 年各区的平均房价( 万元 /平方米) 、人均收入 Oi( 万元 /月) 、平均店租( 万元 /( 月·百平方米)) 和停车位数 Ol( 万个),如表3 所示.

表3 2020年南沙各区社会经济基础数据Table3 Social-economic basic data of Nansha in 2020
基于 2020 年南沙新城各区的相对区位势能、平均房价、人均收入、平均店租和停车位数等数据,采用 SPSS 软件标定效用模型的影响参数为: θY=1.2、θr、θO=0.6、λY=1.15、λr=-0.82、λO= 0.074.另外,参照广州市天河区的相关数据,标定 Gumbel分布的参数为 b=1.05.同样利用 2020年南沙新城各区的交通可达性、平均房价、人均收入、平均店租和平均雇员等数据,标定住宅出售和店铺开业的收益函数的影响参数为:a1= 1.17、a2=0.98、a3=1.03、a4=1.32,c1=3.64、c2=0.23、c3=-1.18.
4.3 模型求解
混合遗传算法采用实数编码,初始种群规模为150, 遗传代数为15000代.取 Tour 为 4,Quantity为 0.5,Shrink 取 1.2,Heuristic 交叉算 子的 Ratio取 1.3.经过试验发现,如果变异算子中的标尺小于 0.9, 很难进入可行域范围,如果太大又容易跌入局部最优解.所以本文最终确定 Gaussian 变异算子中 Scale 取 0.93. 混合遗传算法运行 20 次后平均结果见表4 和图2.对比表3 和表4 中的发现,模型所得的结果与预测结果差距较小,这表明模型参数标定结果是合理的.
表4 2020年南沙新城各区居住选址和活动选址的效用及分布Table4 Residential and activities’ site selection utility and distribution of Nansha in 2020
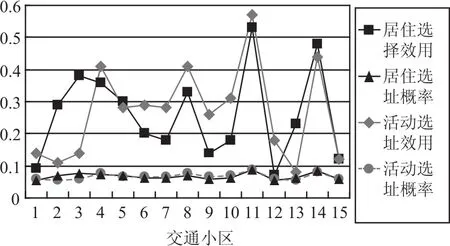
图2 居住选址和活动选址的效用及分布Fig.2 Site selection utility and distribution of resident and activities
表4和图2的结果显示,居住选址的概率从大到小排列,列于前五位的依次为小区 11、14、3、4 和8.尽管小区 8 的交通可达性和人均收入都比小区3 和 4 高,但由于该区位于南沙新城的 CBD,其平均房价为全市最高,高房价极大地影响了人们的住址选择,导致小区 8 的居住选址概率反而较低.同时,外围组团中的小区 2、5 和 13 的居住选择概率均比位于城市中心的小区 7、9、10、12 要大,究其原因,也是城市中心的高房价影响了人们对居住地的选择,同时,中心组团良好的交通可达性弥补了选择在其他组团居住所带来的不便,使得人们更愿意居住在房价较低的小区.此外,活动选址的概率分布基本呈现从中心区向外围区递减的趋势,但小区4 和 14 的活动选址概率相对中心组团的小区 7、8、9、10、12 更高,主要是因为这两个小区的城市综合服务水平较高,交通可达性良好,而且基础产业丰富,服务业种类齐全,极大地吸引了人们到这两个区参与工作上学、娱乐购物、旅游观光等活动.
根据广州市近 20年的家庭平均人口变化趋势,确定南沙新城 2020 年的家庭平均人口数为3.2 人/户.此外,家庭数和店铺数分别以户/100 平方米和店/50 平方米计算,由此确定每个店铺的平均店员数为 0.17,每个店员平均接待顾客数为 10. 36.将以上参数及运算所得的代入模型,可得到南沙新城的人口和就业分布,运算结果如表5和图3所示.
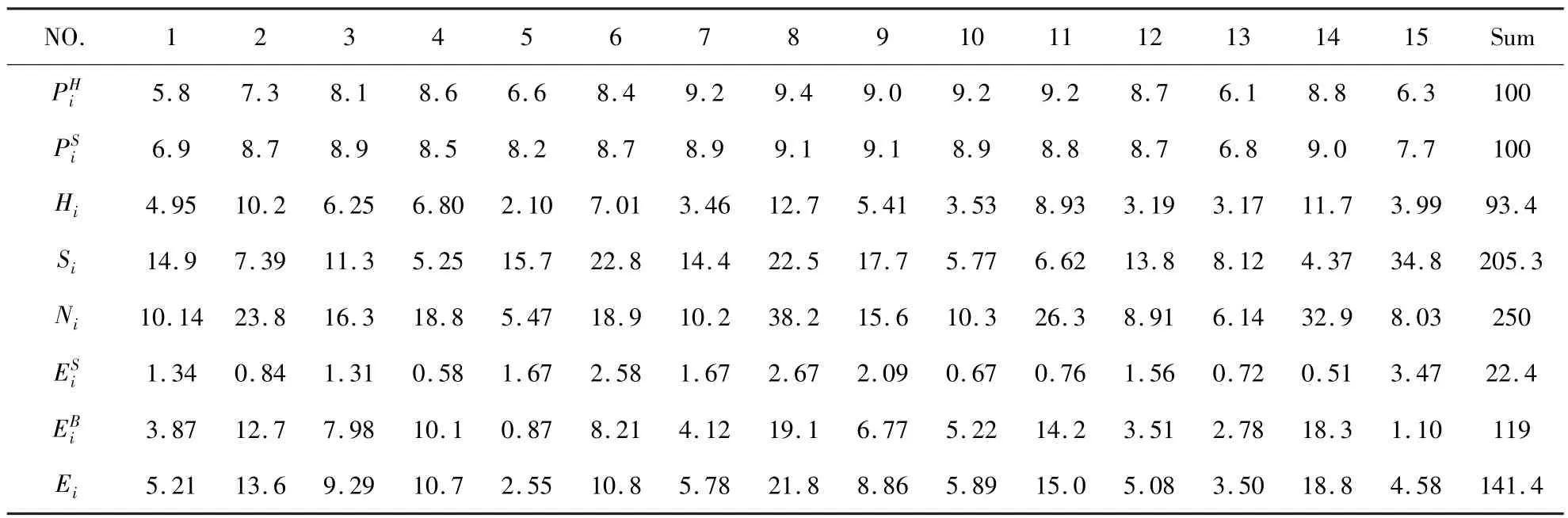
表5 2020年南沙新城各区人口和就业者数(万人)Table5 Population and employment of Nansha new town in 2020(10000 people)
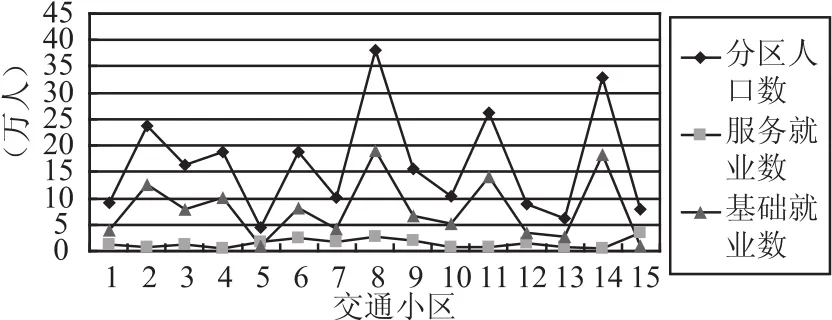
图3 2020年南沙新城各区人口和就业分布Fig.3 The distribution of population and employment in Nansha new town
表5 的结果显示,2020 年南沙新城的总人口将达到 250 万,就业总人口为 141.4 万,其中基础产业就业数为 119 万,明显大于服务业的就业数22.4 万.这主要是因为南沙新城的西部组团和北部组团分别是装备制造基地和汽车产业基地,提供了大量的基础产业就业岗位,而中部组团作为高端产业配套基地,聚集了大量的基础就业岗位.此外,北部组团承担起整个城市的物流和航运功能,也提供了较多的基础产业就业机会.相比之下,服务业的就业数就少得多.由人口数和就业数可求得南沙新城的就业比为 0.57,与本文取值 0.55 极为接近,也符合国内外新城的取值范围(0.48-0.62).
图3的人口分布曲线显示,各小区人口分布极不均匀,人口大多集中在各组团的中心(小区 2、4、8、11 和 14).主要原因是这些小区平均收入较高,住宅密度较大,交通可达性良好,城市服务种类齐全,吸引了大量人口在此居住;而其他小区人数相对较少.就业分布曲线显示,基础产业就业分布呈现不均匀状态,主要集中在小区 2、3、4、6、8、11 和14,正好与这些小区作为装备制造业基地的功能相符;而服务业的就业分布主要集中在中部组团,符合中部组团作为整个城市的商业、金融和服务中心所承担的功能.另外,小区 15 的服务业也占据较大比例,主要是与该区作为整个城市的旅游休闲服务区有关.
5 研究结论
本文利用离散选择理论,对居住选址和活动选址的分布作出了清楚的行为解析;结合新城短期运行的特点,考虑土地租金和交通区位对土地利用的影响,把经济实质引入到土地供需平衡的互动关系中,实现了经济平衡和伴随产生的价格分布,并体现出交通区位对土地利用变化所产生的反馈作用,从而形成具有经济平衡一致性的新城土地利用与交通模型.算法求解结果显示:该模型克服了现有各类 Lowry 模型的缺陷,同时保留了 Lowry 模型的精髓,不仅能对人口分布和就业格局进行合理的调配,而且适用于新城的短期运行.
模型对新城土地利用与交通系统的互动关系能给出合理的模拟解析,但仍未实现动态调整机制,这为模型的下一步发展指明了方向.未来模型还需要根据不同时点的土地利用状况优化变量和参数设置,通过引入土地增长和空置的年度调整函数,对未知参数进行重新标定并修正新的计算结果,从而形成一个不断重复的循环迭代,使模型具有动态性,并验证模型长期运行的平衡一致性.
[1] Chan Y.Location,transport and land-use:Modeling spatial-temporal information[J].Berlin:Springer, 2005:378-499.
[2] Jun Myung-jin,Moose J E.The Lowry model revisited: Incorporating a multizonalinput-output model into an urban land use allocation model[J]. Review of Urban&Regional Development Studies, 2002,14(1):2-17.
[3] Ben-Akiva M,Lerman S.Discrete choice analysis: Theory and application to traveldemand [M]. Cambridge,MA:MIT Press,1985.
[4] Albeverio S,et al.The dynamics of complex urban systems:An interdisciplinary approach[J].Physica-Verlag HD,2008:391-407.
[5] 赵童. 国外城市土地使用-交通系统一体化模型[J]. 经济地理,2000,20(6):79-83.[ZHAO T.A review of integrated land use-transportation models applied in western countries [J]. Economic Geography,2000,20(6):79-83.]
[6] 周彬学, 戴特奇, 梁进社,等. 基于遗传算法的非线性 Lowry 模型模拟研究[J]. 北京大学学报(自然科学 版),2011,47(6):1097-1104.[ZHOU B X,DAI T Q,LIANG J SH,et al.A simulation research of nonlinear Lowry model based on genetic algorithm [J]. Acta Scientiarum Naturalium Universitatis Pekinensis,2011,47(6):1097-1104.]
[7] Mandel B,Gaudry M,Rothengater W.Linear or nonlinear utility functions in logit models:The impact on high rail demand forecasts[J].Transportation Research Part B,1994,(2):91-101.
[8] 杨敏, 陈学武,王炜,等. 基于人口和土地利用的城市新区交通生成预测模型[J].东南大学学报(自然科 学 版 ),2005,35(5):815-819.[YANG M, CHEN X W,WANG W,et al.Trip generation forecasting model of new district based on urban population and land use[J].Journal of Southeast University(Natural Science Edition),2005,35(5): 815-819.]
[9] 张友全,王幼松,郝志彪.广州市商品住宅空置率影响因素的实证分析[J].建筑经济,2012(1):33-36. [ZHANG Y Q,WANG Y S,HAO Z B.The empirical analysis on influence factors of commodity housing vacancy rate in Guangzhou [J]. Construction Economy,2012(1):33-36.]
[10] 罗亚中,袁端才,唐国金.求解非线性方程组的混合遗传算法[J].计算力学学报,2005,22(1):109-114.[LUO Y ZH,YUAN D C,TANG G J.Hybrid genetic algorithm for solving systems of nonlinear equations[J]. Chinese Journal of Computational Mechanics,2005,22(1):109-114.]
Land Use and Transportation Model in New Town
HU Yu-cong,CHEN Hai-wei,LIANG Feng-ming
(School of Civil Engineering and Transportation,South China University of Technology,Guangzhou 510640,China)
In order to simulate the spatial distribution of land use in new town,this paper proposes a land use and Transportation model in new town based on land prices and traffic location.The distribution function of living and activities in Lowry model is firstly revised by discrete choice theory.Meanwhile,the resident's site selection utility is defined as a linear model about land rent and traffic location.And then,a balance equation is set up to simulate the assignment of house and activities,and a hybrid genetic algorithm for solving the model is also presented.At last,Guangzhou Nansha new town is taken as the empirical study area to test and verify the model and algorithm.The results reveal that the model is able to analyze the spatial distribution of land use and provide the basis for rational assignment of population and employment in Nansha new town's short-term development.All these demonstrate the model is effective and available in practice.
traffic engineering;land use and transportation model;location;new town;hybrid genetic algorithm
1009-6744(2014)01-0020-08
U491.1
A
2013-<07-08 class="emphasis_bold">07-08 修回日期:2013-08-17 录用日期:2013-10-1207-08
2013-08-17 录用日期:2013-10-12
国家自然科学基金资助项目(61174188).
胡郁葱(1970-),女,湖北武汉人,副教授,工学博士. *
:ychu@scut.edu.cn

