拥挤收费条件下出租车公司收益优化研究

祝进城, 帅 斌*, 孙朝苑

(1.西南交通大学 交通运输与物流学院,成都 610031;2. 电子科技大学 经济与管理学院,成都 610054)

拥挤收费条件下出租车公司收益优化研究

祝进城1, 帅 斌*1, 孙朝苑2

(1.西南交通大学 交通运输与物流学院,成都 610031;2. 电子科技大学 经济与管理学院,成都 610054)

研究了实施拥挤收费过程中,收费区域内的出租车也需要缴纳拥挤费条件下的出租车公司收益优化问题.考虑私家车、公交车和出租车之间的相互竞争,以及出租车搜寻顾客时间与顾客等待出租车时间对方式划分的影响.采用双层规划模型对问题进行了描述,其中,下层规划为等价于变分不等式的组合网络均衡模型;上层规划为出租车公司的收益最大化.设计了求解模型的启发式算法.算例结果表明,当出租车公司合理分担拥挤收费费用时,其收益将显著提高,并能达到实施拥挤收费之前的水平;此外,随着出租车数量的增加,出租车公司的收益将随之先增加后减小,而出租车公司的最优拥挤收费分担比例则先减小后增加.

城市交通;收益优化;变分不等式;出租车公司;拥挤收费

1 引 言

由于出租车在城市交通中的重要作用与高比例特性(如在香港,某些关键路段出租车占交通量的比例高达 50%-60%[1]),使得在实施拥挤收费过程中,收费区域内的出租车是否也应缴纳拥挤费成为一个非常重要的问题.文献[2]研究了美国曼哈顿与拉瓜迪亚(LaGuardia) 机场之间,拥挤收费对载客出租车(拥挤收费由乘客承担)路径选择与旅行时间的影响.文献[3]比较了出租车拥挤收费前后的社会福利变化.结果表明,通常情况下,在实施拥挤收费过程中,对收费区域内的出租车也征收拥挤费将获得更大的社会福利.

然而,与私家车不同,出租车的实际运营者是出租车公司.当对出租车征收拥挤费时,必须要考虑由于出租车需求量减少导致的出租车公司收益下降问题.直观上,为了消除拥挤收费带来的负面影响,出租车公司可以通过分担部分拥挤收费来提高出租车需求.但是,如果出租车公司承担的拥挤费太高,则其收益可能会下降;反之,其承担的费用太低,则无法保证吸引足够的乘客数,最终导致其收益减少.因此,在对出租车进行拥挤收费时,出租车公司的收益优化是一个需要研究的问题.文献[1,4,5]分析了出租车市场的均衡性质及垄断市场、竞争市场、社会最优条件下的出租车公司收益优化问题.但是,这些研究未考虑拥挤收费对出租车市场带来的影响.

本文通过构建多方式分担模型来刻画对出租车进行拥挤收费条件下的出租车市场变化,进而研究了出租车公司的收益优化问题.采用双层规划模型对该问题进行了描述,其中,下层规划为组合网络均衡模型,刻画了出租车拥挤收费对出行需求、交通方式划分、路径选择以及空驶出租车交通分布带来的影响,并构建了与之等价的变分不等式,上层规划为出租车公司的收益最大化.设计了求解模型的启发式算法.该研究能够为拥挤收费政策制定者与出租车公司提供科学的决策依据.

2 模型相关说明

2.1 基本假设

考虑交通网络 G(V,A),V 为节点集合,A 为路段集合,A-为收费路段集合,¯A⊆A.R为起点集合,S为讫点集合.在任一研究时段,OD对r、s间存在以下需求约束条件:

式中qrs——OD 对 r、s 间的交通需求量;——分别为选择私家车、公交车、出租车的需求量.

此外,采用 m ∈ M=(p,b,c) 表示各交通方式集合.

对于载客出租车而言,满足以下需求守恒方程:

2.2 广义出行费用函数

2.2.1 出租车广义出行费用函数

假设当出租车载客时,拥挤收费由出租车公司与乘客共同承担,其中,乘客承担比例为 θ,出租车公司承担比例为(1- θ).相类似,当出租车空驶时,拥挤收费由出租车驾驶员与出租车公司共同承担,承担比例分别也为 θ与(1- θ),从而可以得到以下路段广义出行费用函数为式 中——分别为私家车、出租车乘客(载客出租车)、空驶出租车的路段广义出行费用;

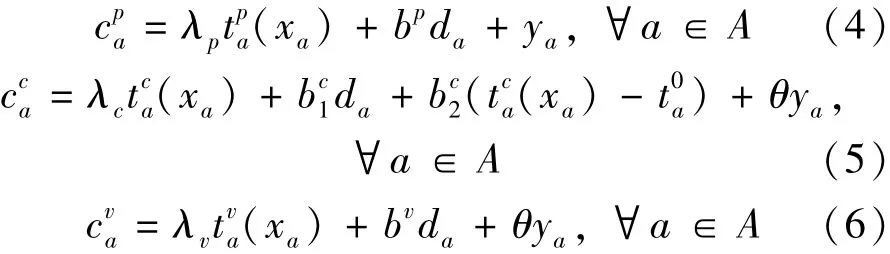
λp——私家车出行者的时间价值;

ta——路段 a ∈ A 上的旅行时间,它是路段流量 xa的增函数;

λc——出租车乘客的时间价值;

λv——出租车驾驶员的时间价值;

bp与 bv——分别为私家车与出租车的单位距离运营成本;

b1c——出租车按距离收取的费用;

ya——路段 a ∈ A 上的拥挤收费费用.相应地,各路径广义出行费用为

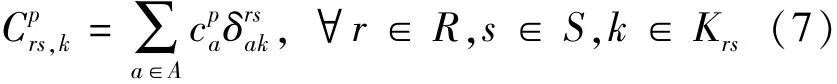
Krs——各交通方式的路径集合.

2.2.2 公交车广义出行费用函数

为鼓励公交出行,对公交车实施免征拥挤费政策.公交车乘客的广义出行费用包括,车内旅行时间、车内拥挤导致的不舒适成本、候车时间、公交票价[7].

λb——公交车乘客的时间价值;

Ga(v) ——车内拥挤导致的不舒适函数;

ζ为拥挤不舒适的单位成本.

类似于文献[8-9],拥挤不舒适函数可表示为

α1与α2——正参数;

Ba—— 路段a∈A上的公交车总容量,式中 U 为单 位公 交车 的平

均载客量;

Frs,l——OD 对 r、s 间线路 l 上的公交发车频率;

Lrs——公交车线路集合.相应地,公交车乘客的路径广义出行费用 C

可表示为

τ——公交票价.

此外,路段交通量 xa可表示为式中——OD 对 r、s 间选择交通方式 m ∈ M在路径k上的流量; fv

sr,k——OD对s、r 间空驶出租车在路径k上的流量;

η ——转化系数,表示将单位公交车转化为等量的私家车数.

2.3 出租车服务时间约束

考虑单位小时内的出租车运营情况.出租车运行时间包括载客时间与空驶时间两部分,其中,出租车总载客时间 TO为完成所有乘客出行需求所需的时间为

式中 hrs——OD 对 r、s 间的平均旅行时间,式为

出租车总空驶时间 TV 为出租车从小区 s∈ S到小区 r∈ R 的行驶时间,以及在小区 r∈ R 内搜索等待顾客的时间为

hsr——小区 s∈ S 与 r ∈ R 间的平均旅行时间为

在单位小时内,总的出租车载客时间与总的出租车空驶时间之和应该等于总的出租车服务时间,即满足以下约束[12]:

式中 N ——单位小时内路网上的出租车数量.

3 下层组合网络均衡模型

3.1 路径选择

采用 Wardrop 均衡原理描述各交通方式的路径选择行为.在均衡状态下满足以下数学式:

同理,对空驶出租车存在以下条件:

式中 uvsr——区域 s∈ S 与区域 r∈ R 间的空驶出租车最小广义出行费用.

3.2 空驶出租车交通分布

由于拥挤收费区域内的出租车也需要缴费,因此,空驶出租车的交通分布会受到拥挤收费的显著影响.假设出租车将乘客送至目的地之后,立刻开始搜寻下一乘客,且每一位出租车驾驶员都是理性的,目标是以最小的期望搜寻费用搜索到乘客.同时,考虑到每位出租车驾驶员的个体特征(驾驶习惯、路网感知等)不同,而出租车乘客的到达是随机的,因此,出租车的期望搜寻费用是一随机变量.我们假设这一随机变量服从 Gumbel分布,因此可采用如下logit 模型来表述空驶出租车的交通分布[13]:

式中 Pr/s——空驶出租车从小区 s ∈ S 出发,在小区r∈R搜索到乘客的概率;

ρ ——一正参数,表示出租车驾驶员对乘客需求及整个出租车市场供给水平的了解程度,ρ越大表示出租车驾驶员掌握的信息越多.

此外,在一个稳定的均衡状态下,路网上的空驶出租车将能满足所有乘客的需求,且每一位乘客在经历等待与搜索之后最终能得到出租车服务,因此,有以下守恒公式[6]:

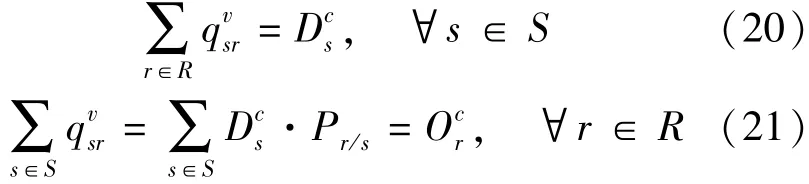
3.3 交通方式选择

出行者的交通方式选择实际上是一个概率问题,我们采用 Logit分离模型进行描述:

3.4 弹性需求

本文采用以下弹性需求函数来描述拥挤收费对 OD 需求量的影响.该函数是 OD 对 r、s间最小广义出行费用的连续单调减函数.

式中 urs——OD 对 r、s 间的最小广义出行费用.

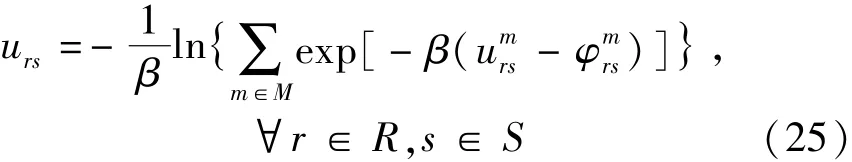
式中 urs——对应的需求函数反函数,

4 等价的变分不等式

考虑到私家车、出租车及公交车的流量相互影响,且这种影响是非对称的,因此,不能直接构造等价的极小值规划模型.本文采用变分不等式来描述上述组合网络均衡模型,其可行域 Ω 如下所示,括号中为对应的拉格朗日因子.

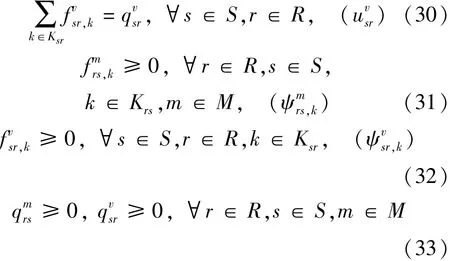
式中 式(26)-式(27)为空驶出租车起讫点流量守恒条件;式(28)表示各交通方式需求量与 OD 总需求的守恒关系;式(29)-式(30)为各交通方式路径流量与需求量守恒关系;式(31)-式(33)为路径流量与需求量的非负约束.

在说明可行域 Ω 之后,相应的变分不等式模型(P1)可描述为

定理1变分不等式模型(P1)等价于上述组合网络均衡模型.

类似文献[3],通过库恩-塔克条件可证明定理1.

由于变分不等式模型(P1)的可行域 Ω 是由一系列非负、线性约束条件组成的,因此,是紧的凸集;同时该变分不等式是带有非负流量约束的连续函数,从而至少存在一个解[13].

5 上层出租车公司收益最大化

在我国,出租车公司主要通过对出租车收取规费来获得利润,因此其收益直接取决于出租车的运营数量.然而事实上,如果乘客需求量减少,出租车驾驶员的效益太低,将导致市场上出租车数量下降,最终出租车公司的收益也将降低.基于此,为了有效反映出租车拥挤收费后,乘客需求量减少对出租车公司收益的影响,本文采用出租车总收入与总成本的差值来描述出租车公司的收益.因此,上层目标函数(P2)可表示为

式中 ξ——出租车的单位小时运营成本.

6 求解算法

本文设计如下启发式算法求解下层变分不等式模型(P1).

步骤0初始化.设迭代次数 j=0,任选一初始解,r∈R,s∈S,k∈Krs,m ∈ M.

步骤1计算最小广义出行费用.根据路径流量计算广义出行费用,以及对应的最小广义出行费用,r∈ R,s∈ S,k ∈ Krs,m ∈ M;然后根据载客出租车路径流量计算出租车乘客起讫点需求量,并通过求解等价于式(19)的双约束重力模型得到空驶出租车的需求量,以及出租车与出租车乘客的等待搜索时间、,从而计算出载客出租车的广义出行费用和对应的最小广义出行费用

步骤2计算需求矩阵.根据弹性需求式(24)、式 (25) 计算总需求 量 qrs, 然后采用基于logit模型的交通方式划分函数式(23) 得到各交通方式需求量,r∈ R,s∈ S,m ∈ M.

步骤3交通量 分配.在得到需求量和之后,通过求解下列固定需求网络平衡问题得到辅助路径流量,r ∈ R,s ∈ S,k ∈ Krs,m ∈ M.

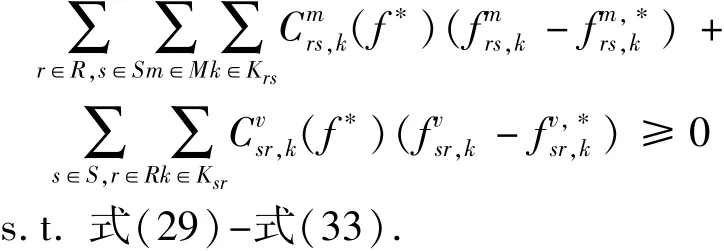
步骤4采用 MSA 技术更新流量.根据以下公式更新路径流量,其中,r∈R,s∈S,k ∈ Krs,m ∈M.

步骤 5收敛性检验.若满足下式,则输出最终结果;否则令 j=j+1,返回步骤 1.

在获得下层变分不等式模型(P1)的解之后,本文采用遗传算法求解整个双层规划模型.

7 算例分析

采用以下交通网络(见图 1)来说明模型与算法的有效性.算例网络包含 4 个 OD 对(1,6)、(1, 4)、(5,6)、(5,4),6 个节点,13 条路径和 14 条路段.公交车线路为 1-3-4-6,1-2-4-3-5-6,1-3-5-6-4,5-3-4-6,5-3-1-2-4-6.

图1 算例网络Fig.1 The example network

旅行时间函数采用如下 BPR 公式:

sa——路段 a 的通行能力,具体值如表 1所示.

需求函数采用负指数函数,其公式为

式中 qrs——OD 对 rs 间的潜在需求;

κrs——需求灵敏度参

表3说明,在拥挤收费区域内的出租车也需要缴纳拥挤费背景下,如果出租车公司合理承担拥挤收费费用(最优承担比例 1- θ=0.17),其收益将得到显著提高,达到了 5 863,远大于出租车公司不承担拥挤费的情况( 该条件下的收益为-13 607),并略高于未实施拥挤收费条件下的收益(为 5 359).导致这一结果的原因为,在对出租车进行拥挤收费时,出租车需求量明显降低( 由 2 812 降到了 2 520),因此出租车公司收益会减小.然而,当出租车公司合理分担拥挤收费费用时,尽管其支付的费用增加了,但由于出租车使用成本降低带来的出租车需求量增加( 由 2 520 提高到 3 378) 仍然会使其收益得到提高.

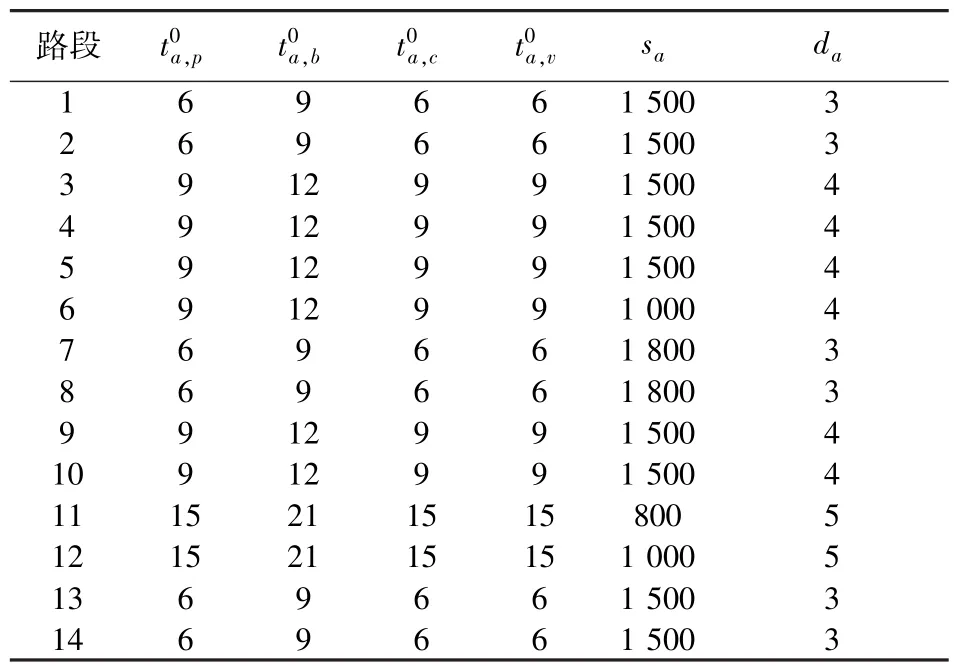
表1 自由流旅行时间、路段通行能力及路段长度______Table 1 Iink free flow,capacity and length

表2 公交车发车频率Table2 Bus frequency

表3 系统结果比较Table3 Comparison of system performance

图2描述了对出租车进行拥挤收费条件下,出租车公司收益与出租车数量之间的关系.图2表明,随着出租车数量的增加,出租车公司的收益呈先增加后减小的趋势.这是因为,起初,出租车公司可以通过增加出租车数量来提高出租车服务水平、吸引乘客数量,从而提高出租车公司收益;然而,当出租车数量增加到一定程度( 超过 2 800),此时,出租车乘客的潜在需求已经非常少,而由于出租车数量增加导致的成本却不断增大,因此,出租车公司的收益开始下降.

图2 出租车公司收益与出租车数量之间的关系Fig.2 The profit of taxi firm against taxi fleet size

图3表明,出租车公司承担的最优拥挤收费比例(1-θ)随着出租车数量的增加而先减小后增大.导致这一结果的原因为,最开始,由于增加出租车数量能够有效吸引乘客数,因此,出租车公司仅需承担较小比例的拥挤费就能提高出租车需求量.然而,随着出租车数量的进一步增加,出租车的潜在需求也随之减少,此时,出租车公司只能依靠扩大承担拥挤收费的比例来减少出租车乘客的使用成本,增加乘客数量.

图3 出租车公司承担的最优拥挤费比例与出租车数量之间的关系Fig.3 The optimal proportion of taxi firm paying toll versus taxi fleet size

8 研究结论

本文研究了在实施拥挤收费过程中,当收费区域内的出租车也需要缴纳拥挤费背景下出租车公司收益优化问题.采用多方式分担的双层规划模型对问题进行了描述.其中,下层规划为组合网络均衡模型,模型中考虑了多方式间的相互竞争及出租车搜寻顾客时间与顾客等待出租车时间对交通方式选择的影响;构建了等价的变分不等式模型.上层规划的目标函数为出租车公司收益最大化.设计了求解模型的启发式算法.算例结果表明,对出租车进行拥挤收费条件下,如果出租车公司合理分担拥挤收费,其收益将明显增加,且能达到实施拥挤收费之前的水平.此外,出租车数量将显著影响出租车公司收益与出租车公司分担拥挤费的最优比例.

本文只考虑了对出租车进行拥挤收费条件下的出租车公司收益优化问题.但事实上,当出租车公司通过分担拥挤收费来提高其收益时,将影响整个系统的社会福利.因此,采用多目标函数同时优化社会福利与出租车公司收益是未来的研究方向.同时,采用实际数据分析也是下一步的工作.

[1] Yang H,Ye M,Tang W H,et al.Regulating taxi services in the presence of congestion externality[J]. Transportation Research Part A,2005,39(1): 17-40.

[2] David A K,Jonathan R P.Slow down,you move too fast:the use of tolls by taxicabs in New York city [C]//Transportation Research Board 91st Annual Meeting,Washington D.C.,2012.

[3] Zhu J C,Xiao F,Liu X B.Taxis in road pricing zone: should they pay the congestion charge?[J].Journal of Advanced Transportation, 2012, Manuscript Submitted for Publication.

[4] Yang H,Wong S C,Wong K I.Demand—supply equilibrium oftaxiservicesin a network under competition and regulation[J]. Transportation Research Part B,2002,36(9):799-819.

[5] Yang H,Yang T.Equilibrium properties of taxi markets with search frictions[J].Transportation Research Part B,2011,45(4):696-713.

[6] Wong K I,Wong S C,Yang H.Modeling urban taxi services in congested road networkswith elastic demand[J].Transportation Research Part B,2001, 35(9):819-842.

[7] Li Z,Lam W H K,Wong S C.Modeling intermodal equilibrium for bimodal transportation system design problems in a linear monocentric city[J]. Transportation Research Part B,2012,46(1): 30-49.

[8] Huang H.Pricing and logit-based mode choice models of a transit and highway system with elastic demand [J].European Journal of Operational Research, 2002,140(3):562-570.

[9] 史峰,周文梁,陈彦,等.基于弹性需求的旅客列车开行方案优化研究[J]. 铁道学报,2008,30 (3):1-6.[SHI F,ZHOU W L,CHEN Y,et al. Optimization study on passenger train plans with elastic demands[J].Journal of the China Railway Society,2008,30(3):1-6.]

[10] De Borger B,Fosgerau M.Information provision by regulated public transport companies [J]. Transportation Research Part B,2012,46(4): 492-510.

[11] Ahn K.Road pricing and bus service policies[J]. JournalofTransportation Economicsand Policy, 2009,43(1):25-53.

[12] Yang H,Wong S C.A network model of urban taxi services[J].Transportation Research Part B,1998, 32(4):235-246.

[13] Wong K I,Wong S C,Yang H,et al.Modeling urban taxi services with multiple user classes and vehicle modes[J].Transportation Research Part B,2008,42 (10):985-1007.

Profit Optimization of Taxi Firm When Charging Taxis with Toll in the Pricing Zone

ZHU Jin-cheng1,SHUAI Bin1,SUN Chao-yuan2
(1.School of Transportation&Logistics,Southwest Jiaotong University,Chengdu 610031,China; 2.School of Management and Economics,University of Electronic Science and Technology of China,Chengdu 610054,China)

The issue that profit optimization of taxi firm is investigated when charging taxis with toll in the pricing zone.The competition among private car,public transit and taxi is introduced and the impact of customer and taxi waiting time on mode split is taken into account.A bi-level programming is proposed, where the lower-level is a combined network equilibrium model formulated as an equivalent variational inequality program.The upper-level aims to maximize the profit of taxi firm.A heuristic algorithm is developed to solve the lower-level formulation,whereas the bi-level problem can be solved by the Genetic Algorithm.The results of numerical example indicate that the profit of taxi firm can be improved when taxi firm reasonably shares the congestion charge with taxi drivers and customers,respectively.Furthermore,as taxi fleet size grows,the profit of taxi firm initially increases and then declines,while the optimal proportion of taxi firm paying the congestion fee originally decreases with fleet size and increases later.

urban traffic;profit optimization;variational inequality;taxi firm;congestion pricing

1009-6744(2014)01-0192-08

U491

A

2013-05-10

2013-07-31录用日期:2013-08-14

国家自然科学基金资助项目(71173177).

祝进城(1986-),男,四川成都人,博士生 .*通讯作者:shuaibin@home.swjtu.edu.cn