桥区航道优化布置设计研究

艾万政,丁天明

(浙江海洋学院 海运与港航建筑工程学院,浙江 舟山 316000)

桥区航道优化布置设计研究

艾万政*,丁天明

(浙江海洋学院 海运与港航建筑工程学院,浙江 舟山 316000)

桥区航道布置与交通事故密切相关.我国关于桥区航道布置规范主要考虑的因素是船舶的船型尺度,并没有考虑船舶的操纵特性和桥区水流条件.如果按照我国的相关规范来设计桥区航道,是不利于船舶通航安全的.因此有必要综合考虑船舶的操纵性、桥区的水流特性及船型尺度来探讨桥区航道的布置方法.本文重点研究了船舶在桥区操纵性及桥区水流特性,并在此基础上提出了桥区顺直航道及桥区弯曲航道的优化布置设计方法.研究结果表明:桥区的航道宽度是布置桥区航道的关键.桥区的航道宽度设计应充分考虑船舶的操纵性及桥墩水流特性;桥区航道宽度应该是船舶航迹带宽度、船舶操纵性所引起的附加宽度、船间距离等参变量的叠加,同时桥区的航道应该布置在桥墩紊流区范围之外.通过以上分析,本文还从船舶操纵理论及统计理论两个角度提出了桥区航道布置方法.

水路运输;交通事故;操纵性;航道宽度;浮标

1 引 言

随着中国经济的高速发展,中国的桥梁建设也越来越多.截止到2010年,中国跨度超过200 m 的跨江或跨海桥梁的数量已经突破400多座.桥梁不仅会给交通运输带来方便,更重要的是桥梁建设能促进经济的发展[1].如舟山跨海大桥构筑出一条全天候的舟山——大陆通道,使舟山从孤悬海中的岛屿,变成同大陆相连的半岛,成为大陆伸向海洋的港口城市.桥梁建设虽然对社会发展带来巨大的驱动力,但是如果桥区的航道布置不合理,桥区通航事故频发,桥梁也有可能成为阻碍经济发展的瓶颈.就拿长江中游的黄石大桥来说,由于大桥选址在水运繁忙而河道弯曲的水域,再加上桥区的航道不够合理,仅在1993年4月16日至9月16日的147 天中,就发生撞桥事故16起,沉船9艘,直接经济损失数百万元.由此看来,合理布置桥区航道,保持水上交通的畅通,对于保障经济持续发展有着重要的现实意义.

桥区航道布置的关键问题是科学论证航道宽度并合理设置浮标.目前我国桥区航道的布置方法,主要是参考《内河通航标准》及《海港总平面设计规范》的相关要求来进行[2].但是这两个法定文献在确定桥区航道布置时,仅以代表船型的尺度来确定航道宽度,并没有考虑船舶的操纵特性和桥区特殊的水流特性.事实上,航道的主要功能是服务于船舶通航,在考虑桥区航道布置时,首当其冲就得考虑船舶的操纵性和桥区水流条件.因此,《内河通航标准》及《海港总平面设计规范》中关于桥区航道布置的规定应该进一步完善.桥区的航道不同于别的航道,由于桥墩的存在,桥区的水流结构复杂,复杂的水流条件是导致船舶撞墩的重要诱因之一.胡旭跃及庄元等人[3-5]认真研究了桥墩的紊流范围,他们认为,紊流区内存在大量的漩涡,不太适合船舶通航,因此桥区的航道应该布置在桥墩紊流范围之外.胡旭跃及庄元等人的观点对于桥区航道的布置有一定的积极意义,但是他们也较少考虑船舶的操纵特性.刘明俊等专家针对桥区通航做了大量的研究工作,他们从船舶操纵的角度研究桥区通航保障问题,取得了较有价值的成果[6].但他们所研究的出发点主要是从宏观上讨论风和水流对船舶运动的影响,较少考虑桥墩特殊的水流条件对船舶通航的影响.

综上所述,国内外专家关于桥区的航道布置问题虽然研究较多,但总的缺陷是不够全面.桥区的航道布置应该综合考虑船舶的操纵特性、桥区水流条件以及代表船型尺度等因素来科学设计.本文的目的,就是在考虑船舶操纵性的基础上,结合桥区的水流条件、船型尺度,来研究桥区航道宽度和浮标的优化布置设计方法.

2 基于船舶操纵理论的桥区航道布置设计

2.1 桥区航道布置应考虑的因素

桥区航道的宽度与交通事故概率密切相关.图1是对某一桥区航道统计出来的交通事故概率与桥区航道宽度的关系曲线[7].图1 中 k 表示交通事故概率,B 表示桥区航道宽度.图1 表明,桥区航道宽度越宽,交通事故发生的概率就越低.但是,桥区航道不可能无限加宽,因为这样会浪费航道资源.同样,桥区的航道也不可能太窄,太窄船舶操纵不便,交通事故会频发.因此对于桥区的航道宽度,应该依据航道设计的通航标准来进行科学设计.航道宽度设计时考虑的因素应包括:代表船舶的航迹带宽度、船与船之间的安全间距、附加宽度、船与桥墩之间的安全间距等.航道的附加宽度主要是由于船舶操纵性而引起的航道加宽值.对于桥区顺直航道而言,最重要的附加宽度应该是风致漂移量及流致漂移量;对于桥区弯曲航道而言,最重要的附加宽度除了风致漂移量及流致漂移量以外,还应考虑船舶过弯甩尾量.

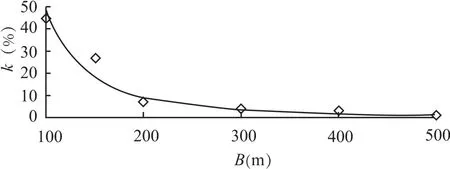
图1 交通事故与航道宽度的关系Fig.1 The relationship between accident and fairway's width

(1)流致漂移量.

流对船舶操纵最大影响是使得船舶产生漂移.船舶在流中航行如图2 所示.设船舶航行的方向与 Y 轴的夹角为 α,船速为 Us,流速为 Uc,流与Y轴的夹角为β.如果船舶沿Y轴方向航行的距离为 S,则船舶沿 X 轴方向产生的漂移量 ΔB1为

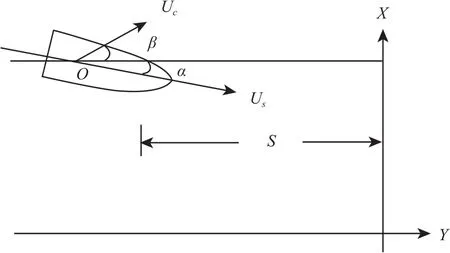
图2 船舶流中航行示意图Fig.2 Ship's navigation in current

(2)风致漂移量.

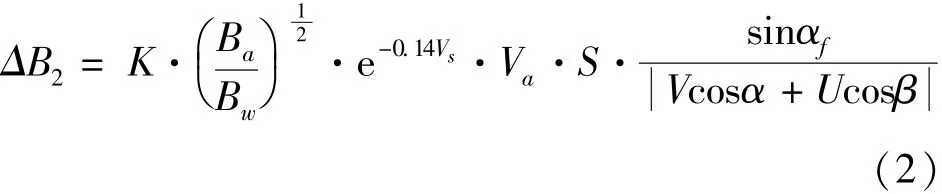
跟流致漂移量的计算方法一样,通过建立适当的坐标系,可以得到船舶在风场中的风致漂移量ΔB2为式中 K 为系数,K=0.038 ～ 0.041;Ba是船体水线以上侧面受风面积(m2);Bw是船体水线以下侧面面积(m2),Bw=L·d(L 为船长,d 为船舶吃水); Vs是船舶的风中航速(kn);Va是相对风速(m/s); af(°)是航道轴向与风向的夹角.

(3)船舶的航迹带宽度.

如图3 所示,如果船舶的船长为 L,船宽为 b,船舶航行偏离航道轴线的夹角为 α,则船舶航向所占的航迹带宽度 Bt为

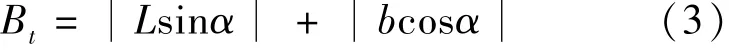
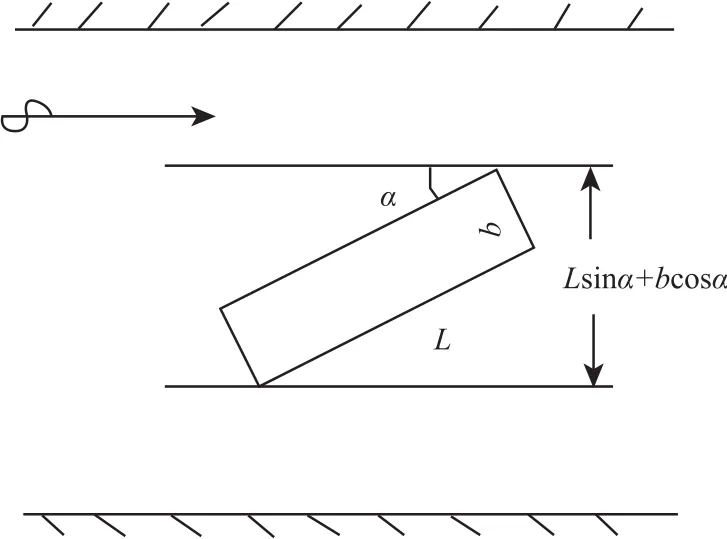
图3 船舶航迹带宽度Fig.3 Ship's track width

(4)船间间距.

船舶之间由于受到水动力的作用会产生船间效应.船间效应是一个较复杂的问题,目前关于船间效应范围的大小只停留在定性分析层面.在设计航道宽度,考虑船舶之间安全间距的时候,必须要考虑到船间效应.日本学者藤井在统计大量船舶交通事故数据的基础上,提出了船舶领域的概念[8].船舶领域模型现普遍应用于分析船舶避碰原理及航行水域的船舶交通流量状况.船舶领域是一船驾驶员将其他船舶和固定物体保持在外的围绕该中心船的有效水域范围.该领域一般可认为是一个椭圆形,领域的大小与船舶尺度、航速以及环境状况有关.对于桥区或限制水域,当船舶以正常速度航行时,其满域尺寸的平均值在船首尾线方向上一般取 6 倍船长,横向上一般取 1.6 倍船长.船舶领域被认为是综合考虑了船间效应等多种因素的综合作用.船舶领域模型如图4 所示.由图4 可知,对于双向航道,船舶之间的安全横间距L至少应为L＞0.8(L1+L2) (4)式中 L1是上水船船长;L2是下水船船长.

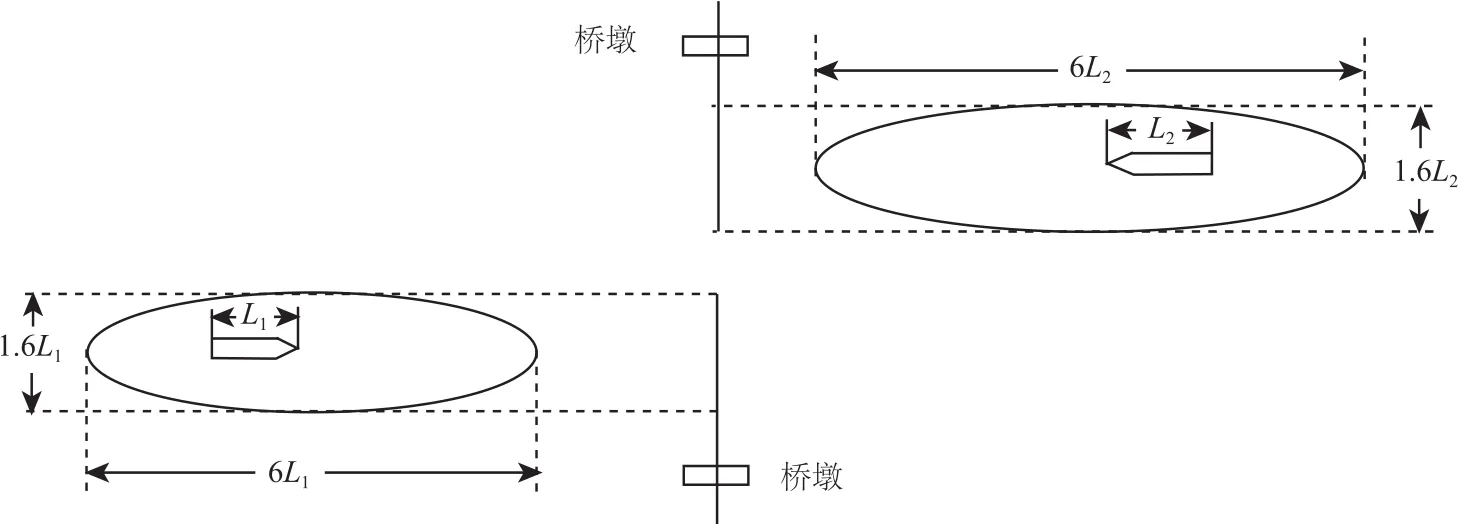
图4 船舶领域范围Fig.4 The scope of ship field

(5)船与桥墩安全间距.

在桥区,由于桥墩的存在,水流遇桥墩必须绕流.在绕流的过程中,在桥墩的迎流面形成驻流,在桥墩的背流面形成汇流,桥墩表面沿航道法线方向存在推船流或吸船流.就船舶的通航安全而言,吸船流对船舶航行最为不利.由于吸船流是在桥墩附近沿着航道宽度方向分布,因此桥墩附近沿航道宽度方向吸船流的最大范围,可作为船舶距离桥墩的最小距离.大量的研究表明,吸船流在航道宽度方向上距离桥墩表面的最大垂直距离K与航道的表面流速 U及桥墩迎流面最大宽度 B密切相关[9-12].本文拟用 RNG k- ε 模型来研究桥墩紊流范围.RNG k- ε 模型的控制方程包括:

①质量守恒方程(连续方程).

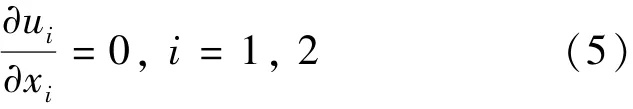
②动量守恒方程.

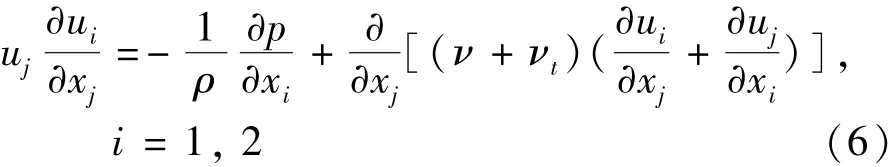
③k-方程.

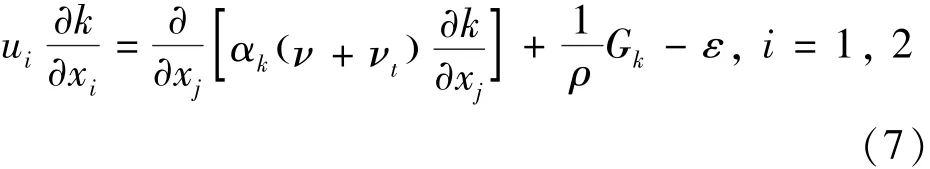
④ ε-方程.

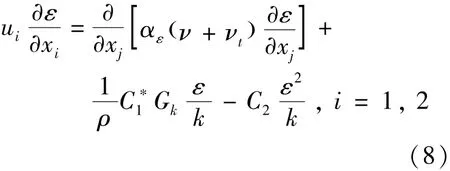
式(5)-式(8) 中相关参数的含义如下:xi(= x,y,z) 为三维坐标轴下的的坐标;ui(=ux,uy,uz)三维坐标轴下的三个轴向流速;ρ是水流的密度;p是压强;ν是水流的动力粘度;νt是涡粘度,νt= Cμ(k2/ε),k 表示紊动能, ε 为紊动能耗散率,Cμ= 0.085.

其他参数的取值为:

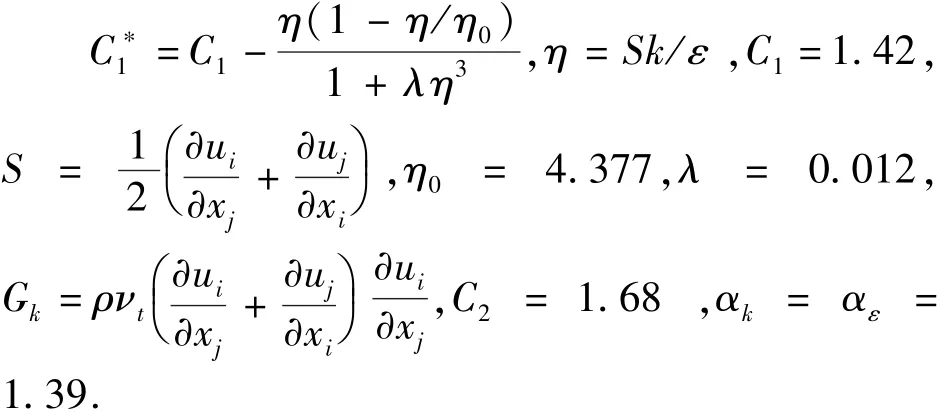
表1是由数值模拟得出的在不同的U和B条件下的K的结果数据.

表1 K数值模拟结果Table1 The K simulation results

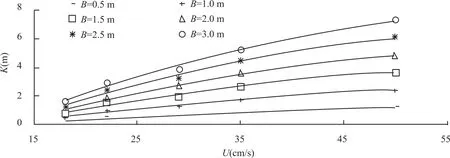
图5 K与相关影响因素之间的关系Fig.5 The relationships between K and relevant factors

表1是数值模拟的结果.将表1中的数据绘制成图5中的曲线并将图5曲线进行拟合,可以得到K的经验表达式如下:

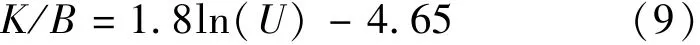
式(9) 的适用范围为:U=18-50 cm/s,B= 0.5-3.0 m,流速 U 的单位是 cm/s,桥墩最大宽度B 的单位是 m,K 的单位也是 m.

2.2 桥区顺直航道布置方法

在布置桥区浮标时,左右浮标之间的航道宽度至少应该叠加以下参数:上下水船舶的风致漂移量、上下水船舶的流致漂移量、上下水船舶的航迹带宽度、上下水船舶之间的横向安全间距.同时桥区的浮标离桥墩的距离至少应大于式(9)所计算出的K的大小.

2.3 桥区弯曲航道布置方法

弯曲航道水深分布不均匀,一般凹岸一侧水深较大,凸岸一侧水深较小.凸岸常淤积边滩,并附有沙嘴、沙脚等淤积物,有的潜伏水下伸入河中甚远,上行船舶沿岸航行不慎易吸浅.弯曲河段主流线弯曲,两岸水势有高低之分,常伴有背脑水、扫弯水、斜流和回流不正常水流,对船舶航行安全不利.因此,弯曲航道桥区航道宽度应该在顺直航道宽度的基础上适当加宽.由于船舶在过弯道时必须经常用舵才能保证船舶航行在航道中心,因此船舶过弯转向存在着以转心为支点的甩尾量,这一甩尾量可以被看作是弯曲航道宽度的加宽值.为计算方便,将弯曲航道近似地看作是半径为 R 的圆弧.这样,船舶在无风、流影响的情况下,船舶过弯甩尾量 B1可分别用下式计算.

(1)当α1＞0、α2≥0 时(如图6 所示).

根据图6,可得

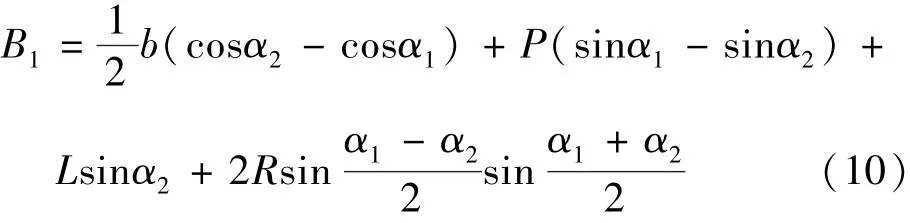
式中 b(m)为船宽;P(m)为转心至船尾的距离; R(m)为弯道曲率半径;α1、α2分别为船舶进入、驶出弯道时的航向角(°),沿航道轴线方向逆时针旋转到船舶首尾线为正,反之为负.

(2)当α1＞0、0≥α2≥-α1时(如图7 所示).

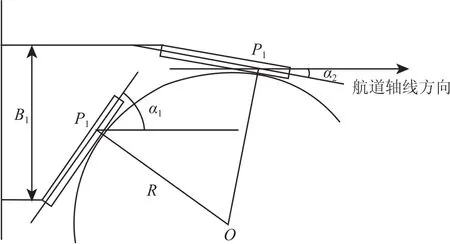
图7 船舶甩尾量(α1＞0、0≥α2≥-α1)Fig.7 Ship's whipping value( α1＞0、0≥α2≥-α1)

根据图7,可得

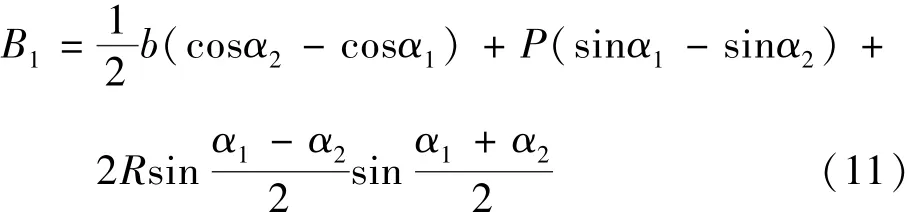
3 基于统计理论的桥区航道布置设计

如前所述,桥区航道宽度设计时应考虑船舶的航迹带宽度、船与船之间的安全间距、附加宽度、船与桥墩之间的安全间距等.如果用统计理论来研究桥区的航道宽度问题,则桥区双向航道通航如图8所示.

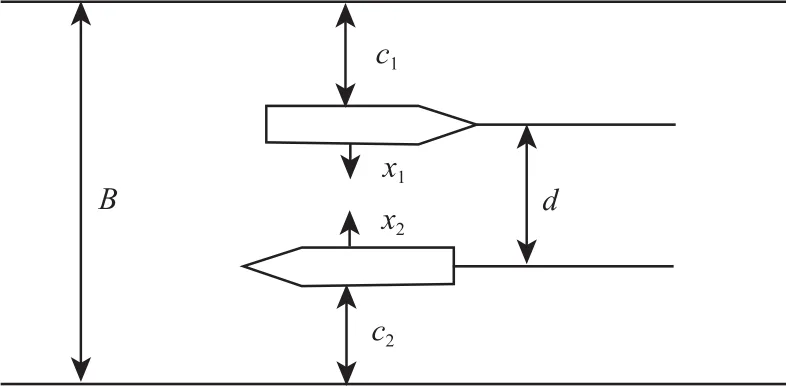
图8 桥区双向航道通航Fig.8 Navigation in double-direction channel

由图8可知,无论是顺直航道的附加宽度还是弯曲航道的附加宽度,附加宽度值均可被认为是船间间距 d 及船与桥墩的安全间距 c1(或 c2)的一部分.船间间距 d、船与桥墩的安全间距 c1(或 c2)均可用数理统计知识来求取.

3.1 船间间距 d

假若 x1为左行船偏离航道航行带轴线的随机概率值,x2为右行船偏离航道航行带轴线的随机概率值,那么船舶间不发生碰撞而安全航行的概率可表示为 P(x1+x2＜d).统计规律表明,随机事件多遵循正态分布,因此相遇船舶间横距分布也可看成正态分布.则船舶安全航行而不发生碰撞的概率为

式中 ρt为两船偏离航道航行带轴线的合均方差.由于左行船和右行船偏离航道航行带轴线的行为可以看成是两个独立的随机变量,且 x1和 x2也遵循正态规律,则由正态叠加原理可得

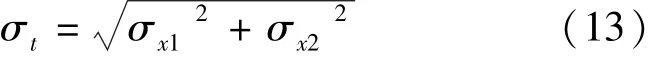
式中 ρx1为左行船偏离航行带轴线的均方差;ρx2为右行船偏离航行带轴线的均方差.

将式(12)变形为

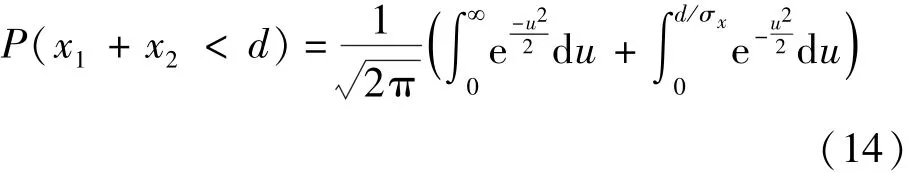
由于

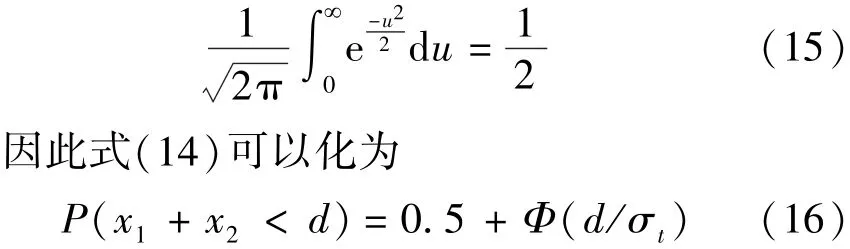
如果令船舶偏离航道航行带轴线而发生碰撞事故的概率为 P1,则 P1为

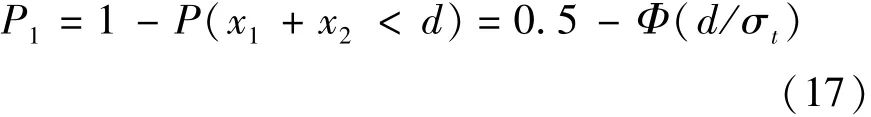
联合式(17)和式(13)可得

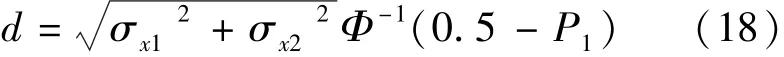
在疏浚和改善航道时,如果事先确定了船舶偏离航道航行带轴线而发生碰撞事故的概率为 P1,同时根据多年统计的均方差 ρx1、ρx2,则完全可确定船间间距d.

3.2 船与桥墩安全间距 c1(或 c2)

假定船舶驶出航道边缘而碰撞桥墩的概率为P2,则两舷驶出航道边缘的概率之和为 2P2.在遵循正态分布规律的前提下,左行船两舷驶出航道边缘的概率可表示为

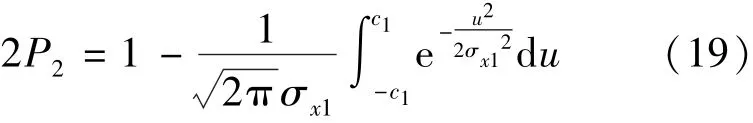
式中 ρx1为船舶驶出航道边缘而碰撞桥墩的均方差.

将式(19)变形为

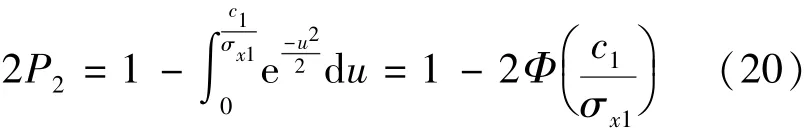
由上式可得

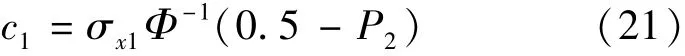
同理可取得右行船与岸壁的安全距离为

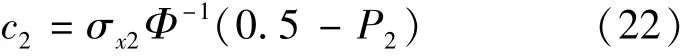
式(21)和式(22)表明,根据多年统计,在事先得知船舶驶出航道边缘而碰撞桥墩的均方差及事故概率的前提下,可以对桥区航道进行优化.

4 研究结论

在充分考虑船舶在桥区操纵特性的基础上,结合桥墩附近的特殊水流结构条件,研究了桥区航道的布置方法.研究结果表明:桥区航道浮标之间的航道宽度应该是船舶航迹带宽度、风致漂移量、流致漂移量、船间安全间距及附加值的叠加;同时,桥区的航道应该布置在桥墩吸船流范围之外.本文还从船舶操纵理论及统计理论两个角度提出了桥区航道的布置方法.

[1] 戴彤宇,聂武,刘伟力.长江干线船撞桥事故分析[J].中国航海,2002(4):44-47.[DAI T Y,NIE W, LIU W L.The analysis of ship-bridge collision in main waterway of The Yangtze River[J].Journal of Navigation of China,2002(4):44-47.]

[2] 中华人民共和国交通部主编.内河通航标准(GB50139-2004)[S].北京:中国计划出版社,2004. 04.[Transportation Department of China.Navigation standard in inland river(GB50139-2004) [S]. Beijing:Beijing Schedule Housing,2004.04.]

[3] 胡旭跃,沈小雄,程永舟,等. 墩柱周围水流表层涡漩区宽度的试验研究[J]. 长沙理工大学学报,2004 (1):39-42.[HU X Y,SHEN X X,CHENG Y Z,et al.Experimental investigation on width of superficial eddy area around cylindrical pier[J].Journal of Changsha University ofScience and Technology (Natural Science),2004(1):39-42.]

[4] 沈小雄,胡旭跃. 航道边线与桥墩之间安全距离的水槽试验研究[J]. 水运工程,2004(11):85-87. [SHEN X X,HU X Y.Safe distance between channel sideline and bridge pier[J].Journal of Port& Waterway Engineering,2004(11):85-87.]

[5] 庄元,刘祖源.桥墩紊流宽度的试验研究[J]. 中国航海,2002(4):5-8.[ZHUANG Yuan,LIU Zu-yuan. Experimental investigation on turbulent flow width around bridge pier[J].Journal of navigation of China,2002(4):5-8.]

[6] 刘明俊, 吕习道. 船舶过弯道所需航宽建模[J].武汉理工大学学报(交通科学与工程版),2006,30 (1):178-182.[LIU M J,LV X D.Necessary width model of ship to getting across channel[J].Journal of Wuhan University ofTechnology (Transportation Science&Engineering),2006,30(1):178-182.]

[7] 齐传新.内河运输安全学[M].大连:大连海运学院出版 社,1991.04.[QI C X.Transportation safety in inland river[M].Dalian:Dalian Maritime University, 1991.04.]

Research on Fairway Layout in Bridge Waters

AI Wan-zheng,DING Tian-ming
(Navigation Shcool,Zhejiang Ocean University,Zhoushan 316000,Zhejiang,China)

Bridge area traffic accident is closely related with fairway layout.The important considered factors in bridge waters fairway layout are mainly ship's dimensions,ship's maneuvering characteristics and water's condition are neglected in Chinese fairway layout regulation.It is adverse to ship's safety navigation if only ship's dimensions are considered in fairway layout engineering.So it is necessary to study fairway layout in bridge waters based on considering all related factors.Ship's maneuvering characteristics,water's condition and the fairway layout method in bridge waters are studied.The results show that fairway's width in bridge waters include ship's track width,distance between ships,additional width caused by ship's maneuvering characteristics.Meanwhile,the fairway in bridge waters should be outside of pier's turbulent scope.Fairway layout methods are put forward by using ship maneuvering theory and statistical theory respectively.

waterway transportation;traffic accidents;maneuvering characteristics;fairway's width;buoy

1009-6744(2014)01-0131-07

U698

A

2013-06-19

2013-08-25录用日期:2013-09-23

浙江省自然科学基金(Y5110084);浙江海洋学院课题(X12ZD02)

艾万政(1971-),男,湖北浠水县人,博士,副教授.*通讯作者:aiwanzheng@126.com