基于参考依赖理论的瓶颈道路收费模型

王 伟,孙会君

(北京交通大学 城市交通复杂系统理论与技术教育部重点实验室, 北京 100044)

通勤者在瓶颈处的排队等待时间为

基于参考依赖理论的瓶颈道路收费模型

王 伟,孙会君*

(北京交通大学 城市交通复杂系统理论与技术教育部重点实验室, 北京 100044)

通勤者每天早晨驾车行驶于一条有瓶颈的道路上,瓶颈处的通行能力是固定的,当通勤者的出发率超过通行能力时,交通拥挤就会发生.本文研究了瓶颈道路上的收费策略以缓解交通拥挤.以最早可接受的到达时间、最理想的到达时间和工作开始时间为参考点,建立了基于参考依赖理论的瓶颈道路模型,分析了用户均衡和系统最优,得到了最优的动态收费策略,进一步提出了两种单阶段收费策略,得出了它们各自的收费水平、收费时间和收费效果.结果表明,单阶段收费策略的效果不但与收费水平和收费时间有关,还与通勤者的参考依赖偏好和损失规避特性有关.

城市交通;单阶段收费;参考依赖;瓶颈模型;出发时刻

1 引 言

经典瓶颈模型假定,通勤者每天早晨驾车行驶于连接生活地与工作地的一条道路上,道路上有一个通行能力有限的瓶颈.所有通勤者都希望在上班时刻到达工作地,但受瓶颈能力约束,总会有一部分人早到,一部分人迟到.早到和迟到的费用称为惩罚费用.出行费用由行驶时间费用和惩罚费用两部分构成.通勤者总是选择令自己的出行费用最小的出发时刻.达到平衡时,所有人的出行费用相等[1,2].

瓶颈模型是动态模型,Vickrey[1]在此基础上提出了最优动态收费策略,即在早高峰期间对通勤者进行收费,某个时刻的收费水平等于不收费平衡时该时刻通勤者的行驶时间费用.这样就能以收费取代行驶时间费用使平衡条件满足,瓶颈满负荷运行且无排队现象.收费并未改变高峰区间,总惩罚费用不变,但总行驶时间费用为最小而达到社会最优.

但由于动态收费策略是时间连续的,实施起来不可行,有些学者用阶段收费策略来逼近最优动态收费策略.在早高峰的某个或多个时间段内实施收费,每个时间段内的收费水平不变.阶段收费虽然不能完全消除排队,但比不收费平衡要好,且易于实施.Arnott等[3,4]最先提出了瓶颈道路单阶段收费策略;Laih[5,6]和 Lindsey 等[7]分别研究了单阶段和多阶段收费策略.Rouwendal等[8]提出一种在瓶颈处既收费又补贴的策略来降低系统的总排队时间.

上述瓶颈模型和收费策略均以“工作开始时间”作为判断通勤者早到或迟到的依据.虽然在“工作开始时间”之后到达工作地会被人们认为是迟到,但在“工作开始时间”之前到达工作地并不一定就被认为是早到.而且“工作开始时间”在人们心目中不一定就是最理想的到达工作地的时间,“最理想的到达时间”一般都会早于“工作开始时间”,在“最理想的到达时间”之前通常又有一个“最早可接受的到达时间”,在这个时间之前到达工作地才会被人们认为是早到.在“最早可接受的到达时间”与“工作开始时间”这个时间段内到达工作地,既不算早到,也不算迟到,都会被人们所接受,因为这个时间段给人们留下了一个工作准备或生活缓冲时间.而在这个时间段内必定有某个时间点是人们心目中的“最理想的到达时间”.

正是基于通勤者的这种心理特性,Senbil 和Kitamura[9,10]和 Jou 等[11]都将“ 最早可接受的到达时间”、“最理想的到达时间”和“工作开始时间”这三个时间点作为参考点,运用累积前景理论研究了通勤者的出发时间选择行为.他们认为通勤者在“最早可接受的到达时间”和“工作开始时间”这两个时间点之间到达工作地会获得收益;在“最理想的到达时间”到达工作地,通勤者获得的收益最大;在“最早可接受的到达时间”之前或在“工作开始时间”之后到达工作地,通勤者都将获得损失.

经典的瓶颈模型和瓶颈道路收费策略均忽略了通勤者对待到达工作地时间的真实心理特性,从而忽视了这种心理特性对出发时间选择和瓶颈道路拥挤的影响.为了弥补以往研究的不足,本文将“最早可接受的到达时间”、“最理想的到达时间”和“工作开始时间”作为参考点,应用参考依赖理论建立新的瓶颈模型,提出基于参考依赖偏好的最优动态收费和单阶段收费策略,为缓解瓶颈处的交通拥挤,提高交通需求管理能力提供参考.

2 基于参考依赖理论的瓶颈模型

下面为本文中使用到的参数和变量:

θ1, θ2——绝对效用函数参数;

φ1,φ2,φ3,φ4——相对效用函数参数;

U(t) —— t时刻出发者的出行效用;

U ——平衡态下的个人出行效用;

D(t) —— t时刻的排队长度;

N ——总出行人数;

s——瓶颈通行能力;

r(t) —— t时刻的出发率;

t——出发时间;

to——最早出发时间;

te——最晚出发时间;

tE——最早可接受的到达时间;

tP——最理想的到达时间;

tW——工作开始时间;

T(t) —— t时刻通勤者的行驶时间;

TTC ——系统的总行驶时间;

τ(t) —— t时刻的收费水平;

TTR ——收费总额.

2.1 参考依赖理论

参考依赖理论认为人们的决策行为依赖于参考点,某个决策方案既会对人们产生一个绝对效用,又会对人们产生一个相对效用(与参考点有关),决策方案的效用由绝对效用和相对效用两部分构成,人们总是选择能产生最高效用值的方案[12,13].Lindsey[14]最先将参考依赖理论应用到道路拥挤收费的研究中,认为通勤者的出行效用由固有效用(绝对效用)和收益-损失效用(相对效用)两部分组成.

本文将参考依赖理论应用到瓶颈模型的研究中,既考虑通勤者的绝对出行效用,又考虑通勤者的相对出行效用.绝对效用与通勤者的行驶时间、排队等待时间和所收取的费用有关,相对效用与到达时间和参考点有关,出行效用由绝对效用和相对效用两部分构成.由于行驶时间、排队等待时间、到达时间和收费水平都由出发时刻决定,所以通勤者的出行效用取决于出发时刻和参考点的选择.每个通勤者对从生活地到工作地的出发时刻进行决策以最大化其出行效用.达到平衡时,所有人的出行效用相同.为了方便起见,本文假设绝对效用和相对效用函数都为线性的,具体的函数表达式见 2.2节.图1和图2分别为绝对效用和相对效用函数.

图1 绝对效用函数Fig.1 The absolute utility function

在图1 中,绝对出行效用始终为负,所以 θ1＜0, θ2＜ 0.在图2 中,tE和 tW之间为收益区,通勤者在此期间到达会获得收益,出行的相对效用为正;通勤者在 tE之前到达或在 tW之后到达都将面临损失,出行的相对效用为负.tE和 tW均是通勤者区分收益与损失的参考点,而 tP是一个“伪”参考点,因为它不是判断收益和损失的标准.但 tP仍然是一个重要的时间点,当到达时间为 tP时,通勤者的收益最大,即出行的相对效用最大.在 tP之前,相对效用函数为到达时间的单调递增函数;在 tP之后,相对效用函数为到达时间的单调递减函数.根据实际情况,一般假设 tP更接近于 tW.由通勤者的损失规避特性可知,直线Ⅰ比直线Ⅱ陡,直线Ⅳ比直线Ⅲ陡;比较早到损失和迟到损失可知,直线Ⅳ比直线Ⅰ要陡.因此,可以得到相对效用函数参数之间的大小关系:φ3＞φ2＞0＞φ1＞φ4,|φ1|＞ |φ2|, |φ4|＞|φ3|.

图2 相对效用函数Fig.2 The relative utility function

2.2 瓶颈模型

N个相同的通勤者每天早晨驾车行驶于连接生活地O与工作地 D 的一条道路上.拥挤发生在一个通行能力有限的瓶颈处(如桥梁、隧道、收费站等),瓶颈通行能力为 s辆/单位时间.当瓶颈处的到达率超过 s时,就会发生排队现象.为了方便分析,假设通勤者从生活地出发即刻达到瓶颈,离开瓶颈即刻到达工作地,通勤者的行驶时间等于在瓶颈处的排队等待时间.排队长度 D(t) 为队中等待通过瓶颈的车辆数:

通勤者在瓶颈处的排队等待时间为

不收费时,通勤者的绝对出行效用由其行驶时间决定,相对出行效用由其到达时间和参考点决定.对 于早到 ( 损失) 的 通 勤者时 间区间内出发),其出行效用为

式中 等式右边第一部分为绝对效用,第二部分为相对效用,下同.

对于早到(收益)的通勤者([tEn,tPn] 时间区间内出发),其出行效用为

对于迟到(收益)的通勤者([tPn,tWn]时间区间内出发),其出行效用为

对于迟到( 损失)的通勤者([tWn,te] 时间区间内出发),其出行效用为

通勤者总是选择使其出行效用最大的出发时刻,当没有一个通勤者能通过单方面改变其出发时刻来增大其出行效用时,系统就达到一种平衡态.如果把 to与 te间的时间区段定义为早高峰期间,那么平衡意味着在早高峰期间内,所有通勤者的出行效用相同.早高峰期间的长度为

to时刻出发的人不会遇到排队,其行驶时间为0,其出行效用为

te时刻出发的人也不会遇到排队,其行驶时间也为0,其出行效用为

根据平衡时等出行效用条件 U(to)=U(te)=U,可得

和

式中 k=tW-tE,k 表示“工作开始时间” 与“最早可接受到达时间”之间的差值.

根据式(3)-式(6) 和式(8)-式(10) 可得到 T(t):

将式(12) 代入式(2) 中,可得到排队长度D(t).再将 D(t) 代入式(1) 中并对两边求导,可得到出发率 r(t):

根据式(13)可得到图3,在图3 中,ABCDE 线表示生活地累计出发人数,AE 线表示工作地累计到达人数.两条线的斜率分别表示出发率 r(t) 和到达率 s.两条线的垂直距离表示排队长度 D(t),水平距离表示通勤者的行驶时间 T(t),即排队时间.总行驶时间(所有通勤者的行驶时间之和)在图3 中表示为区域 ABCDEA 的面积,有

图3 通勤者的出发率和到达率Fig.3 Commuters'departure and arrival rates

2.3 动态收费

上文分析了瓶颈处的用户平衡状态,相应地也会有一个社会最优状态.瓶颈模型中的社会最优是指系统的总排队时间达到最小,即不存在排队.实现社会最优并不改变高峰期 [to,te] 和总早到与迟到时间,第一位、最后一位以及所有的出发者的个人出行效用与用户平衡时的个人出行效用相同,都为 U.但在社会最优状态不存在排队,因此在 [to, te] 期间的出发率与到达率均应为 s.为了驱使系统达到社会最优状态,用户平衡时的排队等待时间可以用某种收费的形式来替代,以维持个人出行效用的均衡,则有:

由于在社会最优时,T(t)=0,得到一个动态收费策略:

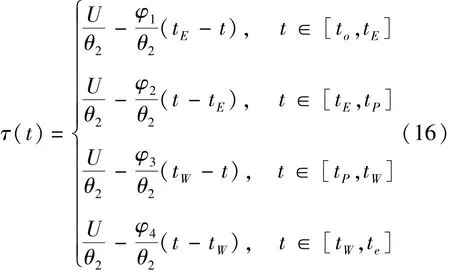
根据式(16) 可知, τ(t) 是一条四段折线,如图4所示,其中

当实施上述动态收费策略时,通勤者会自动调整出发时刻,使 [to,te] 期间的出发率为 s.他们不会遇到排队,但在 t时刻要上缴 τ(t) 的费用.通勤者的个人出行效用仍为 U,与不收费平衡时相比,并没有减少.但由于动态收费是时间连续的,在实际中不可行,下文用单阶段收费来逼近动态收费.单阶段收费虽然不能完全消除排队,但人们在瓶颈处的排队时间比不收费时要少,且易于实施人工收费.

图4 动态收费策略Fig.4 The optimal time-varying toll sheme

3 单阶段收费策略

阶段收费策略是指在早高峰期间的某个或多个时间段内进行收费,该时间段内的收费水平固定.根据收费时间段的多少,可将阶段收费分为单阶段收费、双阶段收费和 M(M ≥ 3) 阶段收费,当 M 趋向于无穷大时,阶段收费趋近于动态收费.由于篇幅的限制,本文只讨论单阶段收费.根据收费时间的不同,可将单阶段收费策略分为两种情形.

3.1 单阶段收费策略一

第一种单阶段收费策略如图5 所示.设 [t+, t-] 为单阶段收费区间, ρ为区间 [t+,t-] 内的收费水平,其中,则有在时间段 [t+,t-] 内对每个通勤者进行收费可以抵消该通勤者的一部分排队时间,所以时间段[t+,t-] 内的收费总额可以抵消一部分的总排队时间.假设此种单阶段收费策略能消除ε′(0＜ε′＜1) 的总排队时间,则有

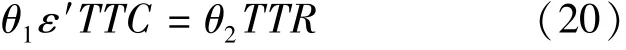
ε′是交通管理部门的决策目标,通过设置不同的目标值 ε′,可得到不同的收费区间 [t+,t-]和不 同 的收 费 水平 ρ,联 立式 (17)- 式 (20)解得:

由上文可知,在最优动态收费策略下, ε′=1.根据式(20)可知,在此种单阶段收费策略下,通过计算 TTR 的最大值可得到 ε′的最大值,联立式(17)-式(19),有

根据一阶最优条件可得:

假设此种单阶段收费策略最多能消除ε′max 的总排队时间,则有

由 φ3＞ φ2＞ 0 ＞ φ1＞ φ4,可知＞ 0, ～φ ＜ 0.假设 N足够大,从而所以,当时,有时,有时,有

3.2 单阶段收费策略二

第二种单阶段收费策略如图6 所示.设 [t+,t-]为单阶段收费区间,ρ为区间 [t+,t-] 内的收费水平,其中 t+∈(t,t),t-∈(t,t),则有

图6 第二种单阶段收费策略Fig.6 The second single-step toll scheme

假设此种单阶段收费最多能消除 ε″max(0 ＜ ε″max＜ 1) 的总排队时间,同理第一种单阶段收费,求得:

否则,此种单阶段收费策略不存在.由于

比较以上两种单阶段收费策略可知,第一种策略收费水平低,但收费时间长;第二种策略收费水平高,但收费时间短.而两种收费策略的收费效果依赖于通勤者参考点的设置和相对效用函数参数的取值.如果 k=0, φ2=- φ1, φ3=- φ4,本文中的瓶颈模型与经典的瓶颈模型相同;另外还可求得,本文的单阶段收费策略最多能减少的总排队时间,与Laih的单阶段收费策略[5,6]相同.

4 研究结论

本文在经典瓶颈模型的基础上,考虑“最早可接受的到达时间”、“最理想的到达时间”和“工作开始时间”这三个参考点,运用参考依赖理论建立了更符合实际情况和通勤者心理的新瓶颈模型,得到了瓶颈道路动态收费策略.但由于动态收费不可行,本文提出了两种单阶段收费策略来逼近动态收费策略,并得出了它们各自的收费水平、收费时间和收费效果.得出结论:基于参考依赖理论的瓶颈模型能准确刻画通勤者的出发时刻选择行为和对到达时间的心理认知;单阶段收费策略的效果不但与收费水平和收费时间有关,还与通勤者的参考依赖偏好和损失规避特性有关;交通管理部门在制定瓶颈道路收费策略时,应考虑通勤者的实际出行心理特性.未来进一步研究的方向有:考虑双阶段和M(M ≥ 3) 阶段收费策略;研究收费再分配策略;根据通勤者不同的时间价值对其进行分类等.

[1] Vickrey W S.Congestion theory and transport investment [J].American Economic Review,1969,34:414-431.

[2] Yang H,Huang H J.Analysis of the time-varying pricing of a bottleneck with elastic demand using optimal control theory[J].Transportation Research Part B,1997,31(6):425-440.

[3] Arnott R,De Palma A,Lindsey R.Economics of a bottleneck[J].Journal of Urban Economics,1990, 27(1):111-130.

[4] Arnott R,De Palma A,Lindsey R.A structural model of peak-period congestion:a traffic bottleneck with elastic demand[J].American Economic Review, 1993,83(1):161-179.

[5] Laih C H.Queuing at a bottleneck with single and multi-step tolls[J].Transportation Research Part A, 1994,28(3):197-208.

[6] Laih C H.Effects of the optimal step toll scheme on equilibrium commuter behavior[J]. Applied Economics,2004,36(1):59-81.

[7] Lindsey R,Van den Berg V,VerhoefE T.Step tolling with bottleneck queuing congestion[J].Journal of Urban Economics,2012,72:46-59.

[8] Rouwendal J,Verhoef E T,Knockaert J.Give or take? Rewards versus charges for a congested bottleneck

[9] Senbil M,Kitamura R.Reference points in commuter departure time choice:a prospect theoretic test of alternative decision frames[J].Journal of Intelligent Transportation Systems,2004,8(1):19-31.

[10] SenbilM,Kitamura R.Heterogeneity in commuter departure time decision:A prospect theoretic approach [J].International Series in Intelligent Technologies, 2005,28:369-398.

[11] Jou R C,Kitamura R,Weng M C,et al.Dynamic commuter departure time choice under uncertainty [J].Transportation Research Part A,2008,42(5): 774-783.

[12] Köszegi B,Rabin M.A model of reference-dependent preference[J].Quarterly Journal of Economics, 2006,121(4),1133-1165.

[13] Munro A,Sugden R.On the theory of referencedependent preferences[J]. Journal of Economic Behavior and Organization,2003,50(4):407-428.

[14] Lindsey R.State-dependent congestion pricing with reference-dependent preferences[J].Transportation Research Part B,2011,45(10):1501-1526.

Pricing Models in a Highway with Bottleneck Based on Reference-dependent Theory

WANG Wei,SUN Hui-jun
(MOE Key Laboratory for Urban Transportation Complex Systems Theory, Beijing Jiaotong University,Beijing 100044,China)

Every morning commuters travel on a highway that has a bottleneck with fixed flow capacity.If the departure rate of commuters exceeds the capacity of bottleneck,the traffic congestion will develop.This paper studies toll schemes designed to alleviate congestion problems that result from a road bottleneck.With three reference points:the earliest acceptable arrival time,the preferred arrival time and the work starting time,a highway bottleneck model based on reference-dependent theory is constructed.The user equilibrium and social optimum are analyzed,and the optimal time-varying toll scheme is given accordingly.Further, two single-step toll schemes are proposed,and the charging level,pricing time and tolling effect of each single-step toll scheme are obtained.The results show that the effect of single-step toll scheme depend on not only the tolling level and the charging time,but also commuters'reference-dependent preference and lossaversion characteristic.

urban traffic;single-step toll;reference-dependentpreference;bottleneck model; departure time

1009-6744(2014)01-0180-07

U491

A

2013-05-20

2013-07-26录用日期:2013-08-14

国家重点基础研究发展计划(2012CB725400);国家自然科学基金(71271023);中央高校基本科研业务费(2012JBZ005).

王伟(1985-),男,湖北黄冈人,博士生.*通讯作者:hjsun1@bjtu.edu.cn